Gambit 软件在《对策论》教学中的应用

王利明

（内蒙古财经大学统计与数学学院，呼和浩特 010070）

Gambit 软件在《对策论》教学中的应用

王利明

（内蒙古财经大学统计与数学学院，呼和浩特 010070）

Gambit是求解对策问题的专用软件，具有操作方便，界面直观，运算速度快等特点。在《对策论》的课堂教学中引入Gambit软件，可以迅速直观地得到计算结果，提高课堂效率，丰富课堂教学内容。

Gambit；对策论；教学研究

0 引言

对策论（Game Theory），也称博弈论，是研究理性局中人在利益相互影响的局势下竞争和合作的理论，在经济、管理、社会、政治、军事、生物等领域都有广泛应用。因此，对策论已成为经济管理类专业学生需要学习的一门专业基础课程。各高等学校的经济学、管理学、数学、统计学等专业都会开设此门课程。对策论通常分为非合作对策和合作对策，在本科教学阶段主要学习非合作对策。非合作对策中最基本的解概念是纳什均衡，通常需要通过求解不等式组、线性方程组或线性规划来得到计算结果。随着局中人人数的增多，策略个数的增加，运算量可能会非常大。在《对策论》的教学课堂上，引入Gambit软件辅助教学，可以迅速直观地得到问题结果。在学生掌握基本计算方法后，省去重复繁琐的计算，提高课堂效率。

Gambit软件是求解对策论的专用软件，可以用来建立对策模型，分析对策结果。最初的版本是1980年代由加州理工学院的McKelvey开发的，经过不断地开发完善，如今已经成为功能强大的对策论计算软件。它拥有直观的图形界面，操作简单方便，包含了所有的非合作对策求解算法。最新的稳定版本是Gambit 15，可以在其官方网站免费下载使用[1]。下面通过两个例子说明Gambit软件在《对策论》教学中的应用。

1 Gambit 软件在《对策论》教学中的应用

1.1 策略型对策

例1求解田忌赛马对策的纳什均衡，支付矩阵见表1。

表1 田忌赛马的支付矩阵

第一步：在计算机桌面点击开始→程序→Gambit，打开Gambit软件。

第二步：在软件操作窗口点击File→New→Strategic game或者点击工具栏的Create a new strategic（table）game图标，新建一个策略型对策。

第三步：默认新建的策略型对策中有两个局中人，每个人有两个策略。可以点击窗口左侧局中人姓名左边的Add a strategy for this player图标为每个局中人增加策略。还可以直接点击修改局中人姓名和策略名称。本例中输入数据后界面见图1。

第四步：点击Tools→Equilibrium或工具栏上的Compute Nash equilibria for this game图标，出现求解界面，见图2。

图1 田忌赛马支付矩阵输入界面

图2 策略型对策求解界面

第五步：在求解界面第一个下拉菜单选择计算纳什均衡的个数，第二个下拉菜单选择求解方法。此处选择求解一个纳什均衡，采用Gambit的推荐算法，得到求解结果，见图3。

图3 例1的求解结果

可以看到得到一个纳什均衡为（（1/3，0，0，1/3，1/3，0），（1/3，0，0，1/3，1/3，0））齐王得到的支付为1，田忌为-1。

1.2 扩展型对策

例2在下面的贝叶斯博弈中，求出所有的贝叶斯纳什均衡。该博弈的具体情况为：

（1）“自然”以相等的概率选择博弈1和博弈2；

（2）局中人1了解自然的选择，但局中人2不了解；

（3）局中人1的策略为T或B，局中人的策略为L或R；

（4）博弈的支付矩阵如下：

表2 博弈1

表3 博弈2

第一步：在计算机桌面点击开始→程序→Gambit，打开Gambit软件。

第二步：在软件操作窗口点击File→New→Extensive game或者点击工具栏的Create a new extensive（tree）game图标，新建一个扩展型对策。

第三步：默认新建的策略型对策中有两个局中人，一个初始结点。可以通过拖拽局中人左边人像图标到某个结点为局中人增加行动，或者选中某个结点后，点击Edit→Insert move为局中人增加行动。同时设置各个结点所在的信息集，最后输入在需要的结点处输入各个局中人的支付。输入完成后的界面见图4。

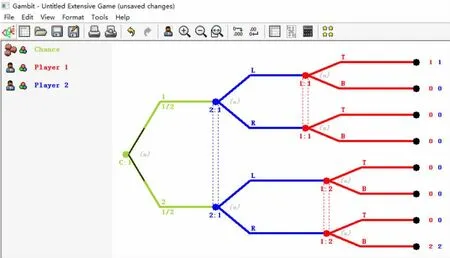
图4 例2的博弈树

第四步：点击Tools→Equilibrium或工具栏上的Compute Nash equilibria for this game图标，出现求解界面，见图5。

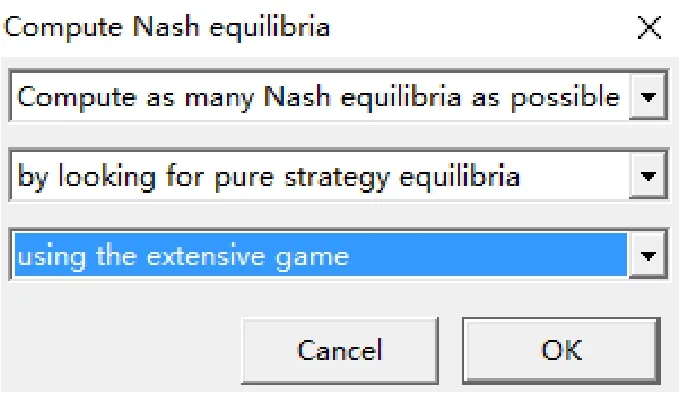
图5 扩展型博弈的求解界面

第五步：与策略型相比，多了一个下拉菜单选择用扩展型博弈还是其对应的策略型博弈求解。此处选择求解尽可能多的纳什均衡，对扩展型博弈寻找纯策略均衡，得到求解结果，见图6。

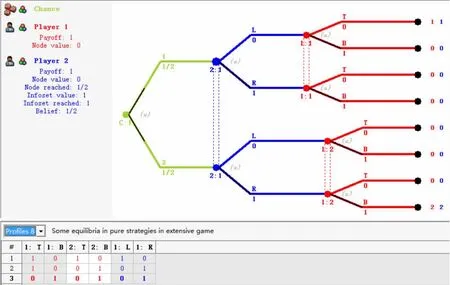
可以看到得到三个纯策略纳什均衡，分别为（（T，T），L），（（T，B），R），（（B，B），R）。

对扩展性博弈来说，还可以通过View→Strategic game命令得到与其对应的策略型博弈，里对应的策略型博弈，见图7。

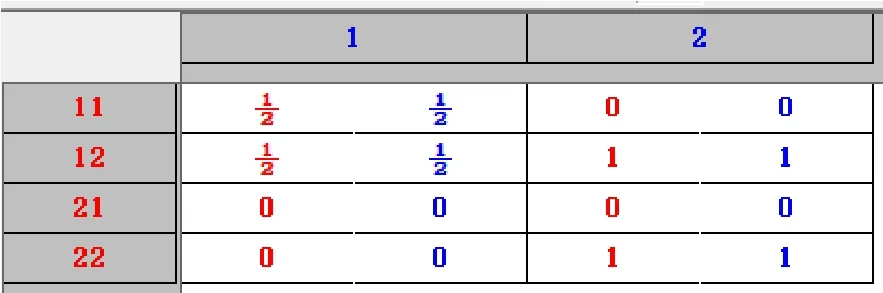
图7 例2对应的策略型博弈

3 结语

对于纳什均衡的求解来说，随着问题规模的增加计算量可能会非常巨大。因此，在《对策论》课堂教学中引入Gambit软件，可以让学生迅速直观地得到求解结果，还可以探索分析一些规模稍大的对策问题，提高学生的学习兴趣和学习积极性。Gambit软件只能求解非合作对策，如果需要求解合作对策的解，如核心、核仁、Shapley值等，还需配合其他数学软件的使用。

[1]McKelvey,Richard D.,McLennan,Andrew M.,Turocy,Theodore L.（2015）.Gambit:Software Tools for Game Theory,Version 15.1.0. http://www.gambit-project.org.

[2]谢政.对策论[M].国防科技大学出版社,2004.

[3]王文举.经济博弈论基础[M].高等教育出版社,2010.

The Application of Gambit in the Teaching of Game Theory

WANG Li-ming

（School of Statistics and Mathematics,Inner Mongolia University of Finance and Economics，Hohhot 010070）

Gambit is a specialized software for game theory which has the characteristics of convenient operation,intuitive interface and fast speed of calculation.By introducing Gambit in game theory teaching,the results can be calculated fast,the teaching efficiency can be improved and the teaching contents can be enriched.

Gambit;Game Theory;Teaching Research

1007-1423（2017）07-0018-04

10.3969/j.issn.1007-1423.2017.07.005

王利明（1983-），男，内蒙古财经大学教师，博士生，研究方向为对策论、多目标优化

2017-02-06

2017-03-01