考虑备用电源的MCS配电网可靠性评估

常学佳，郑焕坤，常鲜戎，李 倩

(1. 华北电力大学电气与电子工程学院，河北保定071003；2. 国网山西省电力公司检修分公司，山西太原030000)

考虑备用电源的MCS配电网可靠性评估

常学佳1，郑焕坤1，常鲜戎1，李 倩2

(1. 华北电力大学电气与电子工程学院，河北保定071003；2. 国网山西省电力公司检修分公司，山西太原030000)

准确进行配电网可靠性评估，对配电系统规划和安全经济运行具有重要意义。针对当配电网母线、馈线分支较多且含备用电源时，传统方法评估效果下降的问题，提出了一种面向元件组且适用于含备用电源情况的改进MCS(蒙特卡洛模拟)评估算法。介绍了面向元件组区域划分和编号的原则、方法。考虑到系统有足够大容量的备用电源时，备用电源能保护到的区域的负荷可持续供电能力得到改善，将负荷的类型设为3，故障修复时间变为联络开关的切换时间。用元件层级的概念进行修正得到含备用电源的负荷故障类型矩阵。以IEEE RTBS BUS6系统的F4馈线为评估对象，利用方差系数检验了改进MCS的收敛性，并分析了收敛精度与结果误差的关系，算例结果验证了所提算法的有效性。

配电网可靠性；MCS评估算法；面向分区；收敛精度

0 引言

据统计，80%的用户停电故障是由配电环节故障引起的，并且配电网投资约占整个供电系统投资的60%[1]。准确的进行配电网可靠性评估，对配电系统规划和安全经济运行具有重要意义。

配电网可靠性评估指标的计算方法总体上可分为解析法和MCS法两大类[2]。当系统规模较小且元件失效概率较小时，解析法更有效，但系统状态的维数会随着设备的增加呈指数增长，进而导致维数灾问题[3-4]。MCS法可分为序贯MCS法和非序贯MCS法[5]，前者是基于有时间概念的分布参数，因此分析结果更精确、更灵活，并且能计算风险指标统计概率的分布，但其对数据、CPU时间、存储空间的要求更高[6]。传统MCS法计算效率低、维数高、难于从高维的概率分布函数中抽样，且MCS法采用的抽样方法产生独立随机序列，序列中各元素之间没有关系，而这并不符合实际电力系统的特点。MCMC将随机过程中的马尔可夫过程引入到蒙特卡洛模拟中，实现动态蒙特卡洛模拟[7-10]。MCMC法考虑了系统各个状态间的相互影响，相比于随机采样的MCS法得到的独立样本序列，更准确地模拟了系统运行的实际情况。但由于系统各个部分的计算模型和算法的差异性，对整个系统进行风险评估是不现实的[11]。文献[12]提出了一种计及分块和层级结构融合的可靠性评估算法，适合于分析含重要电力用户的配电系统的可靠性；文献[13-14]提出了一种基于故障集分类的可靠性评估算法，能够显著提高计算效率，适合于对大型电力系统的可靠性评估。

针对含备用电源的配电网，提出了面向分区的改进MCS可靠性评估算法。以系统分区为基础，用改进MCS法实现了配电网的可靠性评估。以IEEE RTBS BUS6系统中的馈线F4作为待评估系统进行了仿真。

1 MCS计算可靠性原理

MCS法基本原理是建立适当的概率模型，使模型的解为所求解[15-18]。因此对系统元件工作状态建立适当的概率模型，进行大量随机抽样统计实验，结合故障判据，判断该系统状态下所有负荷点的故障类型，对相应参数进行统计，在一定的模拟时间和收敛精度条件下，计算负荷点和系统的可靠性参数。

1.1 元件状态的概率模型

假设元件的故障均为可修复故障。此条件下，指数概率分布能较好的描述元件的故障参数，TTF(故障持续时间)的概率密度为f(t)：

(1)

相应的失效分布函数为F(t)=1-e-λt=δ，δ为(0,1)之间的随机数。然后利用元件的故障率λ和修复率μ，将δ转化为TTF和TTR(故障修复时间)，以下参数的单位均以年记，公式如下：

TTR=-lnδ/λ

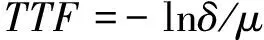
(2)

1.2 抽样原理

设所需的量x是随机变量ξ的期望值E(ξ)，可根据ξ的概率分布函数对ξ进行N次随机试验或抽样，产生相互独立的ξ值序列ξ1，ξ2，…ξN，并计算其算术平均值为：

当N充分大时，有：

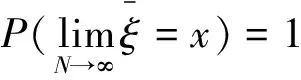
根据大数定律，可以证明：

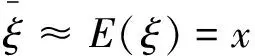
对于配电网中的任一元件i，其每一状态x，有与之对应的状态概率P(x)，设故障率为λ，则P(x)可以表示为：

(3)

当所求量是随机变量的其它数学特征或函数时，可利用相应分布函数，对抽样值进行处理后再统计。

1.3 收敛条件判定

适当的收敛判据是确保MCS精度的关键，变量的方差系数β常被用作终止抽样的判据，β越小变量越趋于稳定。

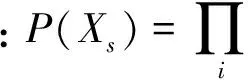
式中：F(X)是系统指标函数；F(Xi)为第i次抽样中的观测值，实际MCS计算中由于抽样次数一般小于系统状态数N，因此得到的只是两者的估计值E(F),V(E(F))，计算如下：

(4)

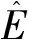
(5)

方差的变异系数β常作为计算精度和计算收敛的判据，其与抽样次数N、指标均值E(F)的关系如下：

(6)

系统越安全，指标均值E(F)越小，则相同的精度β下，抽样次数越多。

1.4 可靠性指标的计算

负荷点i的平均故障率λi，平均故障修复时间ri，平均故障持续时间Ui，计算公式如下：

ri=TTRi/fi

(7)

式中：fi表示总故障次数。设在总仿真年限Tset内，对于负荷点i，年故障次数为k(一般步长取1)的累计年数为fi(k)，则负荷点i年故障次数为k的概率为：

(8)

2 面向元件组的MCS可靠性评估

2.1 区域划分的原则和方法

利用开关元件为界先对配电网进行区域划分，形成元件组和负荷区[19-20]。以分区为单位，面向元件组分析对负荷区可靠性的影响，可以降低研究问题的维度、复杂度，提高评估效率。

(1)区域划分的原则与方法

原则：将元件组等效为一个可靠性参数已知的元件，同一元件组中任一元件故障导致的任一负荷区故障后果模式相同；同一负荷区中任一负荷点对相同元件组对应的故障类型相同。

方法：以负荷为起点至与其相邻最近的断路器或者分段开关，此区域内只能有一个开关元件，且不同区域不可包含同一开关元件。该区域中包含的所有元件称为元件组[16]，包含的所有负荷点称为负荷区。

(2)区域编号原则

馈线的等级：主电源至联络开关(备用电源)之间的线路为主馈线，为第一等级，区域内开关的首端连接到主馈线的为第二等级，开关首端连接到第二层级馈线的区域为第三等级，依次标注。

区域的层级：根据划分区域首端馈线的等级，确定区域的层级，同一层级内按照距离主电源的远近，由小到大进行编号，该层级区域全部标号后再依次标注下一层级。

2.2 模型准备

简单配电网示意图如图1所示，分区后简化图如图2所示。

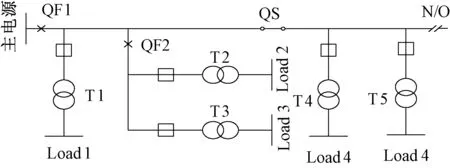
图1 简单配电网示意图

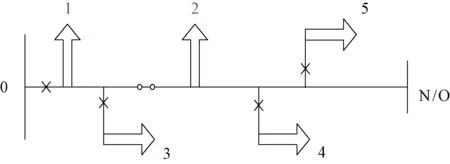
图2 配电网分区简化示意图

(1)对系统进行分区，并对元件组和负荷区进行编号。元件组标号已标于图中，元件组1，2为层级1，元件组3、4、5为层级2。

(2)对元件组标注类型。已假设熔断器完全可靠，则与负荷点所在支路上元件故障，对其余支路负荷没有影响，设元件类型为0。因此，仅考虑与负荷非直接相连的元件对负荷的影响，设元件类型为1。对类型0的元件，标注所连接负荷点的序号(序号不是原系统图中的编号)。

(3)建立每个负荷区同上一层负荷区的关系向量SC和两者间连接方式向量LJ。

上一层负荷区应为离主馈线侧最近的负荷区标号，如图中区域2的SC元素应为1。且主电源根负荷区的上一层负荷区标号记为0，图中区域1的上层记为0。LJ矩阵中，1：断路器连接，2：分段开关连接。

(4)建立每个负荷区所连接的上一层负荷区关系矩阵SJ和对应的上层负荷区数量向量NSJ。图2中区域2的SJ应为区域3，NSJ为1。

(5)负荷分类。根据元件组对负荷是否造成影响和故障持续时间对负荷进行分类：

0类：完全不受影响；

第1类：受影响，故障持续时间为元件故障恢复时间；

第2类：受影响，故障持续时间为分段开关动作时间；

第3类：受影响，故障持续时间为联络开关动作时间。

2.3 模型建立

元件组编号为行编号，负荷区的编号为列编号，以元件组i为例，建立负荷类型矩阵H。流程图如图3。

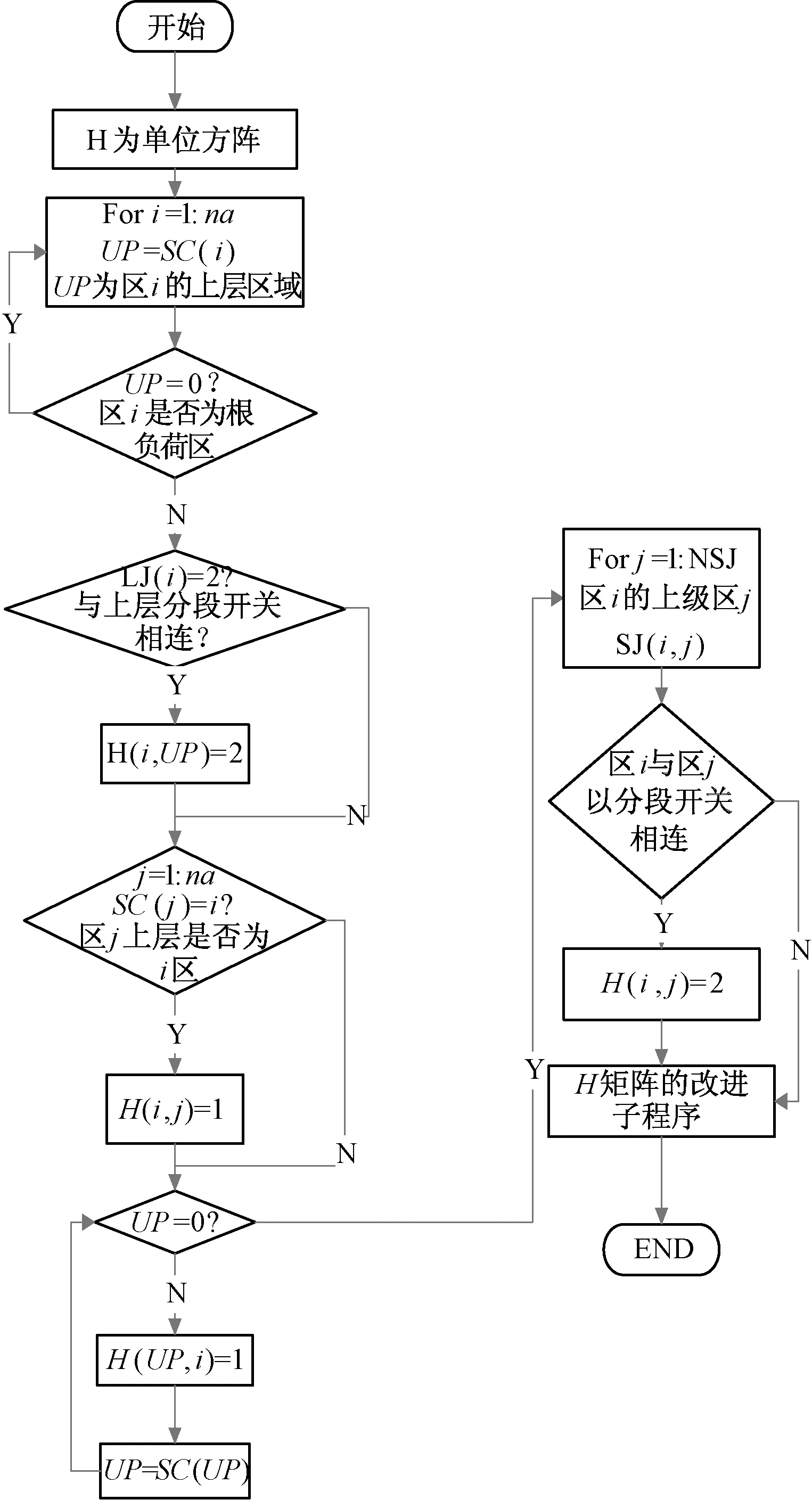
图3 负荷故障类型生成流程图

2.4 模型验证

以图1为例，SC向量元素为(0,1,1,2,2)，LJ向量元素为(0,2,1,1,1)。SJ元素为(0,3,0,0,4)，对应NSJ元素为(0,1,0,0,1)。根据图3所示的算法流程图得到的负荷类型矩阵H如表1。

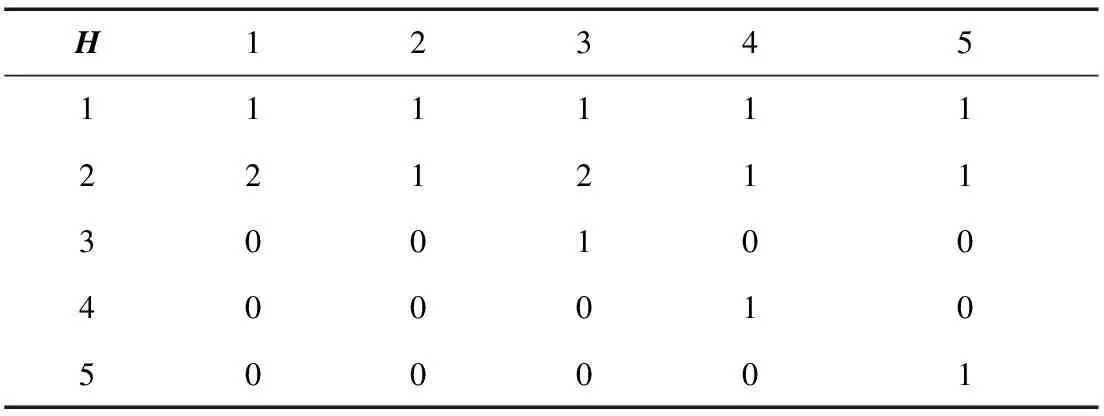
表1 负荷故障类型矩阵

运算结果与FMEA(故障模式后果分析法[21-22])分析结果相同，说明此模型正确。

2.5 模型改进

如果考虑系统有备用电源，对于备用电源能保护到的区域，该区域的负荷的可持续供电能力得到改善，负荷的类型设为3，故障修复时间变为联络开关的切换时间。依然利用上层结构的思想，并通过负荷区层级的概念，判断联络开关闭合后，能否在备用电源与待判断负荷区间形成通路。改进算法流程图如图4。

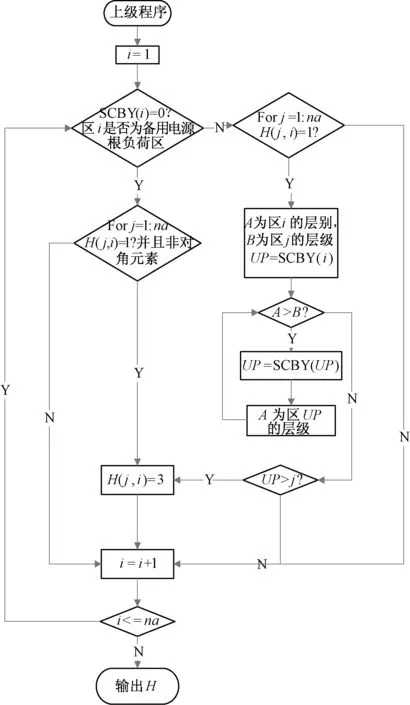
图4 含备用电源负荷故障类型生成流程图

SCBY元素为(2,0,2,0,0);LJBY元素为(2,0,2,0,0); 改进后的负荷区故障类型矩阵如表2所示。

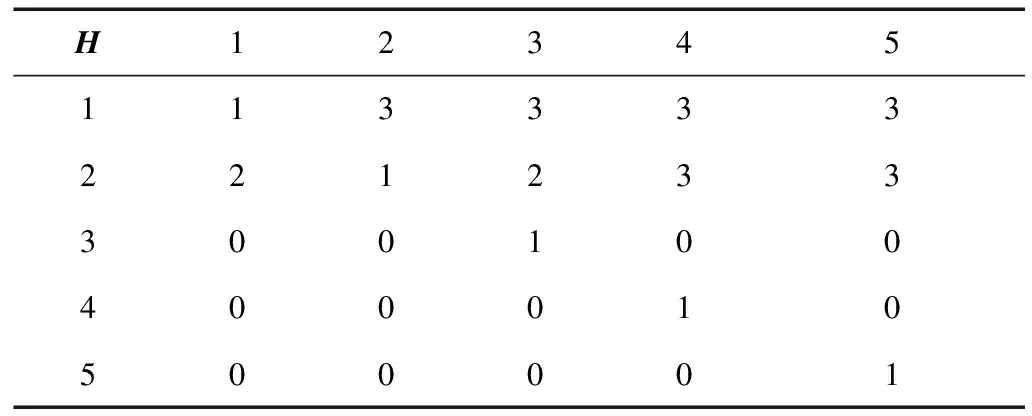
表2 改进后的负荷区故障类型矩阵

改进MCS法可靠性评估流程图如图5。

图5 改进MCS可靠性评估流程图

3 实例验证

3.1 待评估系统参数预处理

本文选用IEEE RTBS BUS6中的馈线F4作为待评估系统。该系统包括23个负荷、23个熔断器、23台配变、30条线路、4台断路器和1个分段开关。开关个数远少于元件个数，分支较多。假设断路器和熔断器可靠概率均为1，变压器有备用，只考虑1阶故障。将待评估系统参数进行预处理，得MCS法负荷类型模型所需的矩阵信息如表3所示。

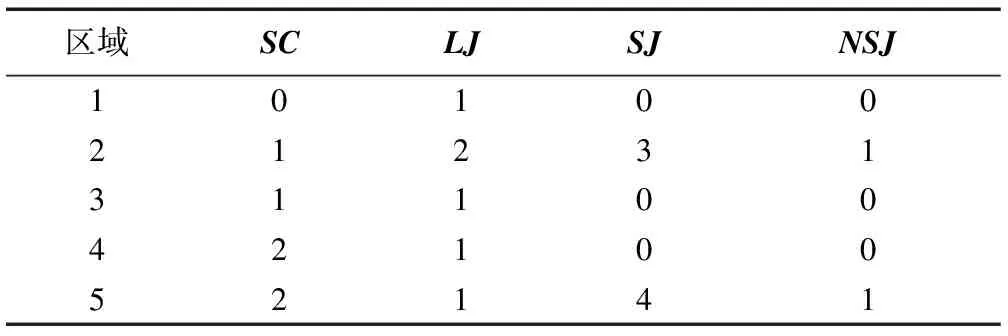
表3 预处理数据向量表

3.2 评估结果

从以下三个方面检验所提方法的可行性。

3.2.1 MCS程序的收敛性分析

(1)收敛性影响因素

本文MCS程序的运行结果呈现收敛状态，对于不同精度要求对应的仿真时长下，程序的收敛判据β的变化情况如表4所示。

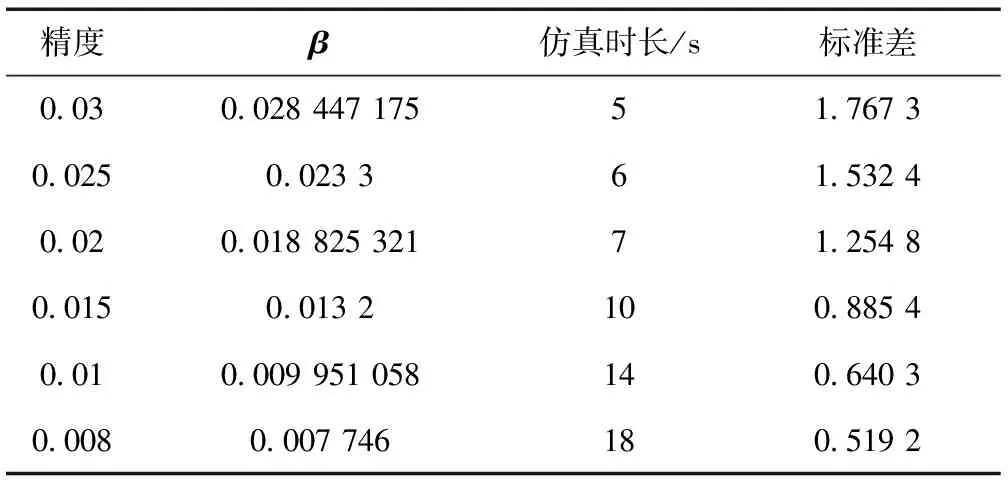
表4 MCS收敛精度与仿真时长关系表

注：仿真时长=仿真次数*1 000a。

方差系数β与抽样次数Ns和方差V(F)的关系如下：

(9)

通过表4数据结果可得图6。

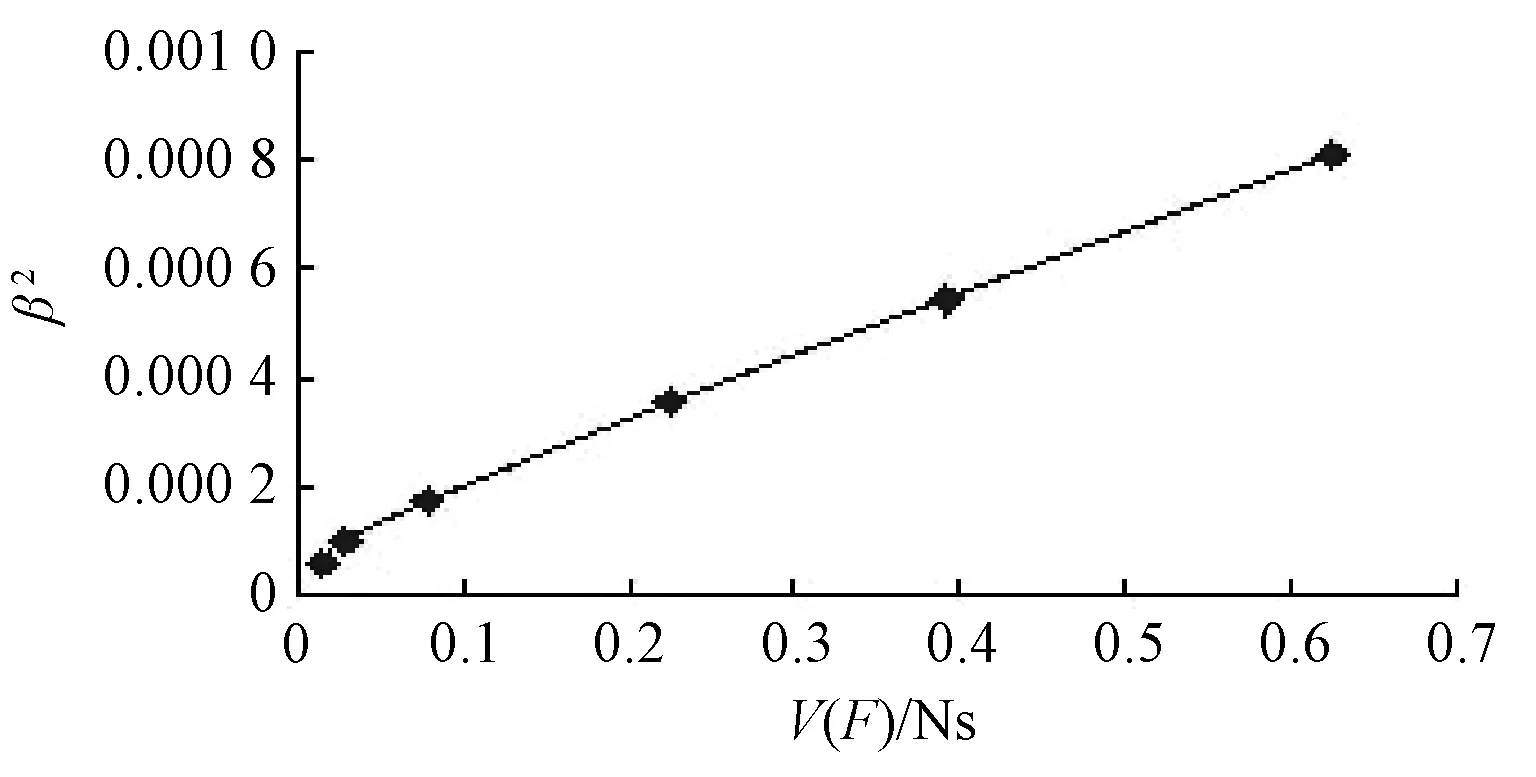
图6 方差系数与方差/抽样次数关系

方差系数β的平方与V(F)/Ns基本呈正比例关系，验证了本程序收敛性的正确性。可以通过降低方差和增加抽样次数的方法提高精度。一般忽略方差的影响，通过改变仿真时间来改变精度，两者的关系如图7。

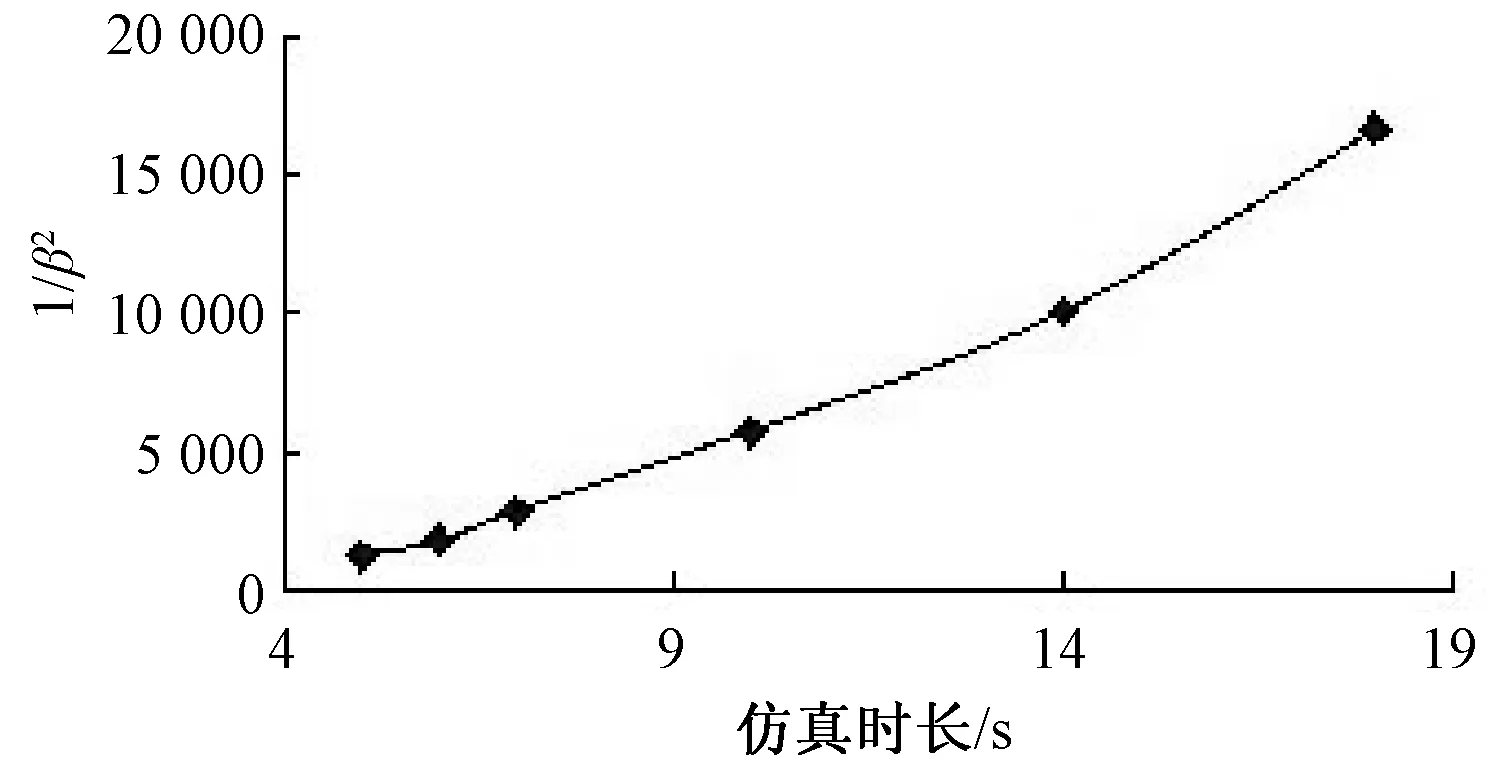
图7 方差系数与仿真时间的关系

1/β^2与仿真时长基本呈正比。仿真时长越长，计算精度越高，指标越接近真值。

(2)收敛的速度

收敛速度可由β表示，其变化规律如图8。

随着仿真时间的增加，β逐渐变小，说明指标逐渐逼近真值，但减小的幅度越来越小。经公式推导，得到β与抽样次数的关系如下：

(10)

可见，β随抽样次数(时间)的减小率变小而减小，当达到一定的精度要求下，在增加精度要求会严重增加仿真耗时。

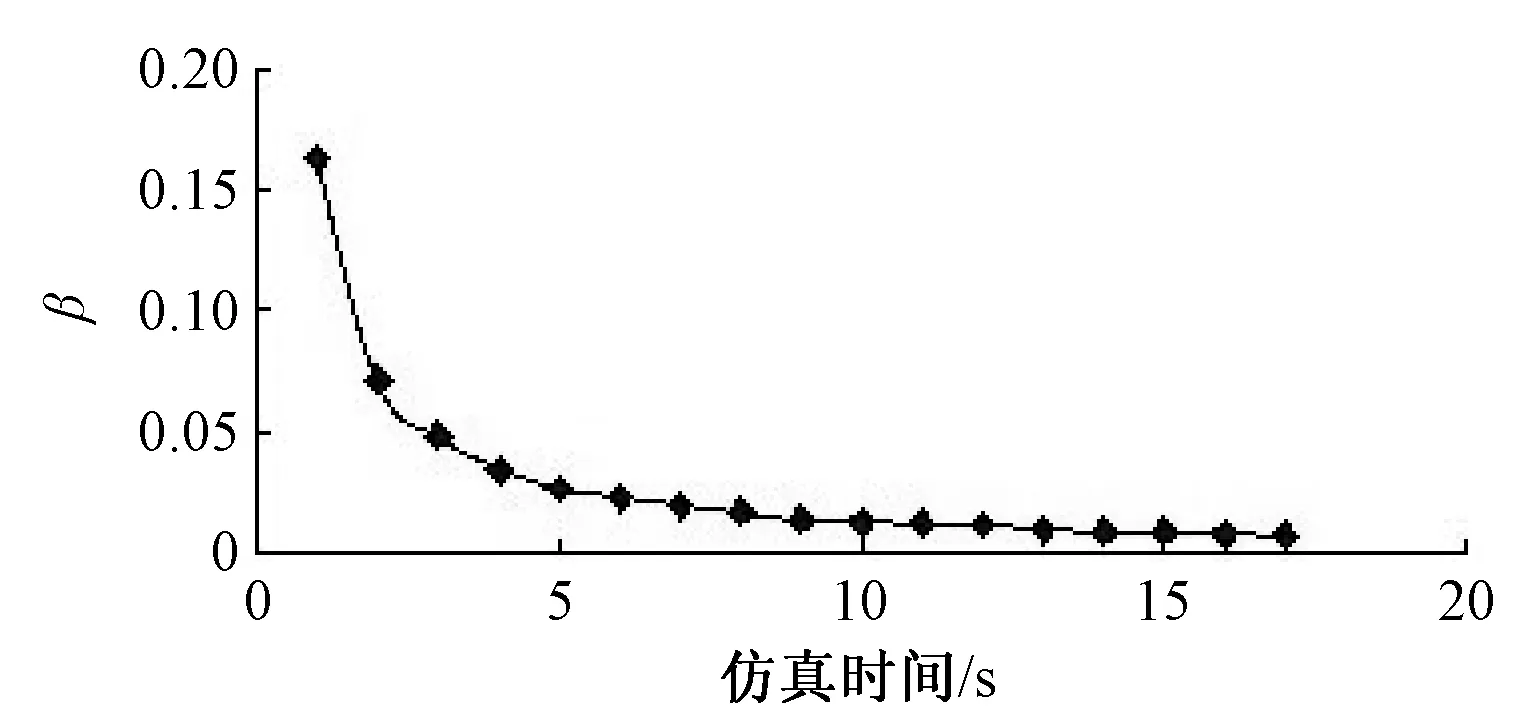
图8 收敛速度与仿真时间关系

3.2.2 MCS评估结果与解析法结果对比

运用本文所提算法求得的部分负荷点和系统可靠性指标如表5所示(方差系数精度为0.01)。

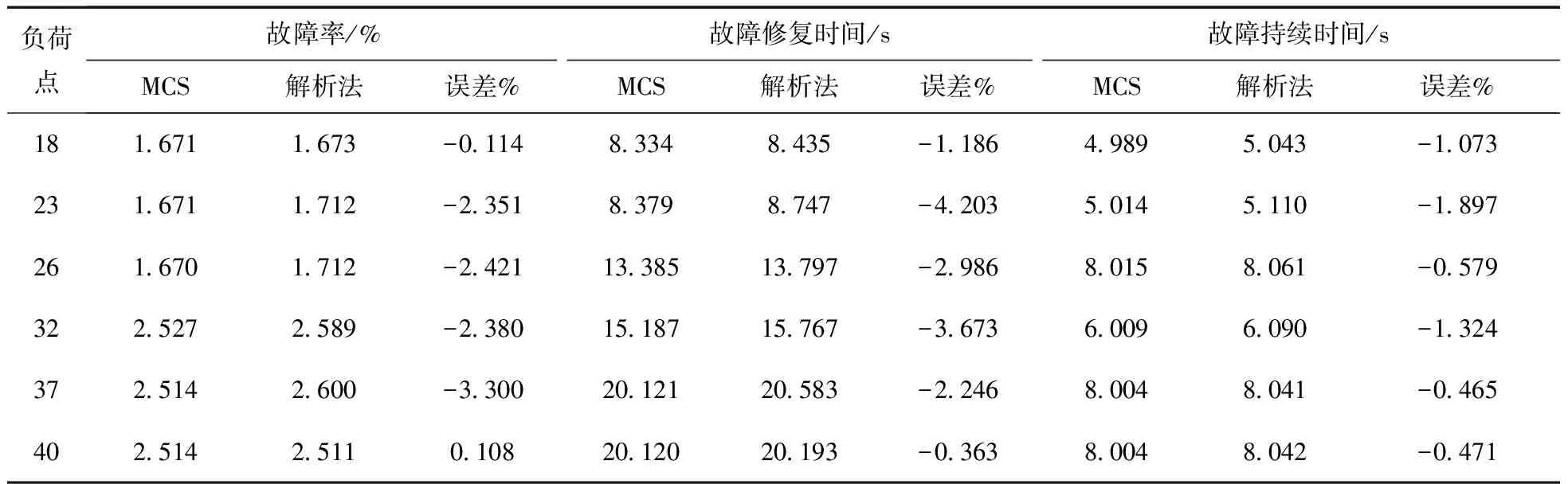
表5 部分负荷点系统可靠性指标对照表

3.2.3 MCS不同精度下的结果误差

在相同可靠性参数的条件下，设置不同的收敛精度要求，得到了可靠性指标。选取部分典型的负荷点，以传统FMEA结果为基准求得误差，进行对比分析，结果如表6、表7所示。

从评估结果可以看出:

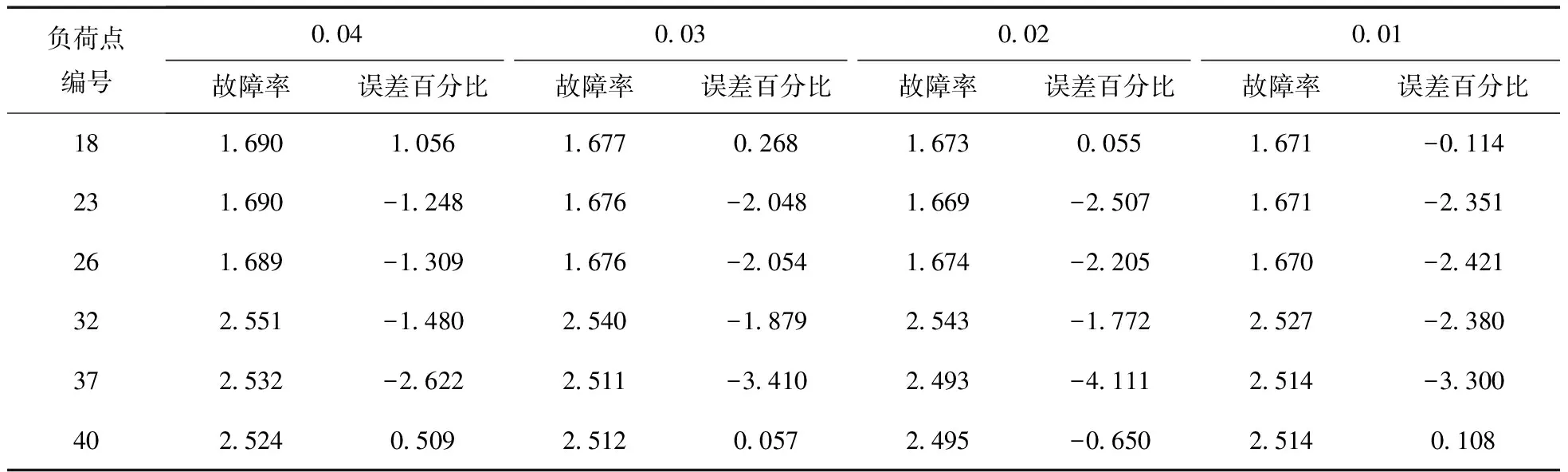
表6 MCS法在不同精度下求得的故障率误差百分比

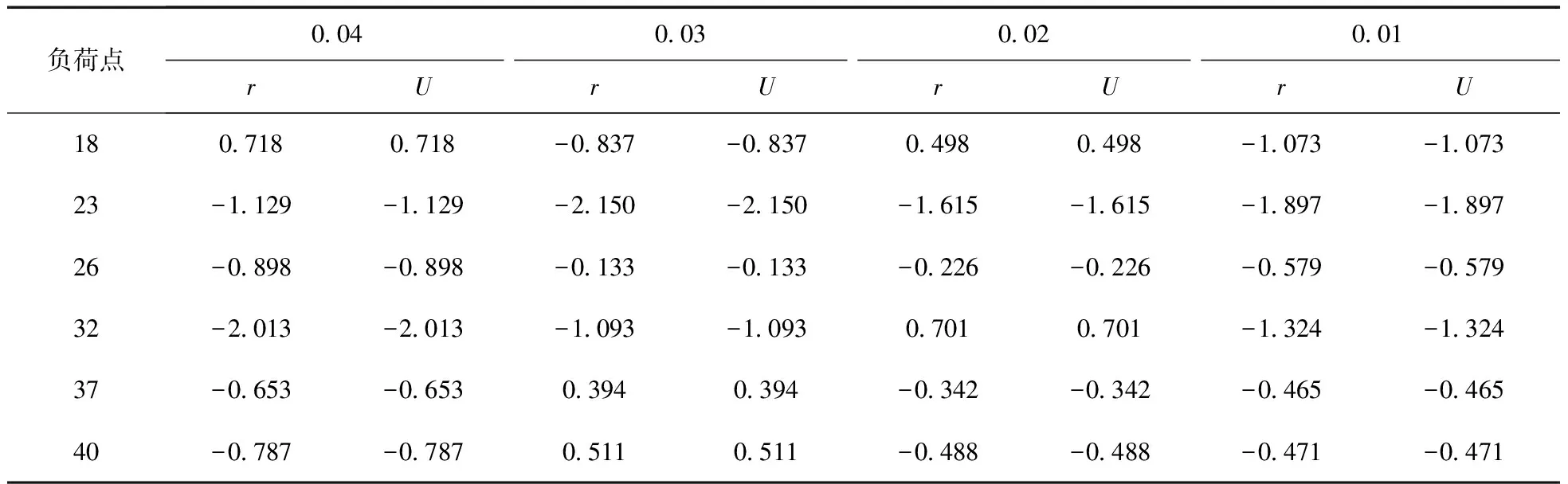
表7 MCS法在不同精度下求得的故障修复时间和停电时间误差百分比

(1)在上述收敛精度下，本文的改进MCS算法与传统FMEA法的负荷点可靠性参数相比，结果误差均很小。3个参数6个典型负荷点中最大的误差没有超过3%，说明所提算法是可行的。

(2)相同负荷，不同参数的收敛情况不太一致。这是因为不同指标的收敛情况不同，本文选择了一般情况下收敛速度最慢的EENS指标的方差系数为收敛判据。若要提高程序的计算效果，可以增加判断变量，得到更全面的精度要求。

(3)同一精度要求下评估结果不完全一致，这体现了MCS算法的随机试验的本质。

(4)一般情况下可靠性指标随精度的增加越来越接近真值。由表6、表7可见，在精度要求为0.04时对IEEE RTBS BUS6系统F4馈线算例进行评估，评估结果已经可以达到较好的效果。

4 结论

本文由上层分区向量、分区连接方式向量，建立了自动生成负荷故障类型矩阵的模型。并用元件层级的概念进行修正，所提面向分区的改进MCS法可以适用于有备用电源的情况。以IEEE RTBS BUS6系统的F4馈线为评估对象，利用方差系数检验了MCS的收敛性，与FMEA结果对比验证了程序的准确性，并分析了收敛精度与结果误差的关系。可以适用于有分支馈线的复杂配电网的可靠性评估。

但所建立的模型没有考虑多备用电源的情况，且采用的指标没有加入配电网的实时潮流。同时，如何选择收敛精度才能确保评估结果的误差在可以接受的范围内也是今后研究的方向。

[1]周家启，赵霞.电力系统风险评估方法和应用实例研究[J].中国电力，2006，39(8)：77-81.

[2]鲍晓慧，侯慧.电力系统可靠性评估述评[J].武汉大学学报(工学版)，2008，41(4)：96-101.

[3]许可，鲜杏，程杰，等.城市高压配电网典型接线的可靠性经济分析[J].电力科学与工程，2015，31(7)：12-18.

[4]王博，游大海，尹项根，等．基于多因素分析的复杂电力系统安全风险评估体系[J]．电网技术，2011，35(1)：40-45．

[5]陈连栋，吕春梅.基于模糊综合评判的电力风险评估方法的研究[J].电力科学与工程，2010，26(11)：50-54.

[6]张富春，吕景顺，范迪铭，等.基于潮流转移识别的电力系统连锁故障风险评估模型[J].电力科学与工程，2013，29(12)：8-12.

[7]XIAO F，MCCALLEY J D．Power system risk assessment and control in a multi-objective framework[J]．IEEE Transaction on Power Systems，2009，24(1)：78-85．

[8]BILLINTON R，LI W．Reliability assessment of electric power systems using Monte Carlo method[M]．New York：Plenum Press，1994：1-6，33-38．

[9]BILLINTON R，ALLAN R．Reliability evaluation of power systems[M]．New York：Plenum Press，1996：3-8．

[10]刘青，戚中译.基于蒙特卡洛法的电动汽车负荷预测建模[J].电力科学与工程，2014，30(10)：14-19.

[11]石文辉，别朝红，王锡凡．大型电力系统可靠性评估中的马尔科夫链蒙特卡罗方法[J]．中国电机工程学报，2008，28(4)：9-15．

[12]殷月喜，李炜，徐岩，等.基于故障区域识别及信息时序属性的电网故障诊断[J].电力科学与工程，2012，28(12)：68-72.

[13]吴素农，吴文传，张伯明．考虑传输容量约束的配电网可靠性快速评估[J]．电网技术，2009，33(14)：21-25．

[14]林济铿，王旭东，郑卫洪，等．基于网络化简的计及开关故障配电网可靠性评估[J]．电力系统自动化，2009，33(9)：32-36．

[15]陈璨，吴文传，张伯明，等．基于元件组的复杂配电网可靠性评估[J]．电网技术，2012，36(8)：81-86．

[16]王枫，祁彦鹏，傅正财.面向开关的复杂配电网可靠性评估简化模型[J].电力系统及其自动化学报，2015，27(2)：57-62.

[17]丁明, 张静, 李生虎. 基于序贯蒙特卡罗仿真的配电网可靠性评估模型[J]. 电网技术, 2004, 28(3):38-42.

[18]文艳, 罗安, 谷群辉. 配电网可靠性分层评估算法[J]. 电力系统保护与控制, 2004, 32(9):31-34.

[19]田奎. 非序贯蒙特卡洛法在发电系统可靠性评估中的应用[J]. 计算机与数字工程, 2013, 41(6):1021-1023.

[20]卢锦玲, 杨晓东, 粟然,等. 一种基于贝叶斯网络的配电网可靠性评估方法[J]. 华北电力大学学报(自然科学版), 2004，31(2):16-19.

[21]田世力, 黄艺, 许自纲. 一种对复杂辐射状配电网进行可靠性评估的实用算法[J]. 电力科学与工程, 2009, 25(3):50-54.

[22]程德才, 赵书强, 马燕峰. 配电网可靠性指标的灰色组合预测方法及应用[J]. 电力科学与工程, 2009, 25(3):18-21.

《电力科学与工程 》

欢迎投稿

欢迎订阅

投稿网址：http://www.dlkxygc.com

Reliability Evaluation of MCS Distribution Network Considering Standby Power Supply

CHANG Xuejia1，ZHENG Huankun1，CHANG Xianrong1，LI Qian2

(1. School of Electrical and Electronic Engineering，North China Electric Power University，Baoding 071003, China;2. Maintenance Branch of State Grid Shanxi Electric Power Company，Taiyuan 030000, China)

Accurate and rapid assessment of distribution network reliability is of great significance to the distribution system planning and safe and economic operation. With the standby power supply and lots of distribution network buses and the feeder branch, the effectiveness of the traditional MCS method declines. In the case of standby power supply, this paper proposes a method to improve the MCS evaluation algorithm. This paper introduces the principle and method of component oriented area dividing and numbering. Considering that the capacity of the standby power is large enough, the region that the standby power can protect has been improved. So the type of load is set to 3 and the fault repair time becomes switching time of the contact switch. The concept of component level is used to modify the load fault type matrix. The RTBS F4 feeder is used as an example to show that the proposed method can be used for the reliability evaluation of the complex distribution network with branch feeders and the relationship between the convergence accuracy and error of the results is analyzed.

distribution network reliability; MCS evaluation algorithm; partition oriented; convergence precision

10.3969/j.ISSN.1672-0792.2017.03.004

2016-10-31。

TM711

A

1672-0792(2017)03-0018-08

常学佳(1990-)，男，硕士研究生，研究方向为电力系统分析与控制。