基于遗传算法的电缆优化分割系统的研究与开发
2017-04-21李胜华万书亭
刘 亚,李胜华,袁 莉,万书亭
(1. 华北电力大学能源动力与机械工程学院,河北保定071003; 2.国网江苏省泰州供电公司,江苏泰州225300)
基于遗传算法的电缆优化分割系统的研究与开发
刘 亚1,李胜华2,袁 莉2,万书亭1
(1. 华北电力大学能源动力与机械工程学院,河北保定071003; 2.国网江苏省泰州供电公司,江苏泰州225300)
电力电缆的优化分割问题属于一维下料问题,针对多规格一维下料问题,在核心算法方面,提出了一种基于遗传算法的求解方法。主要内容是把电缆原材料编号的一种顺序作为一个个体的染色体进行编码,其中的每个编号就代表着一个基因,基因数量为所有需求电缆的数量和,同时,根据建立的数学模型确定适应度函数,在种群进化过程中,应用适应度函数进行评价,通过选择、交叉、变异得到最优解。系统的算法由MATLAB工具实现,界面由VS工具实现,通过两种工具混合编程实现软件的编写。实验结果表明,系统计算速度较快,较好地解决了电缆优化分割问题。
电缆;优化分割;一维下料;遗传算法
0 引言
电力电缆是电网建设的主要原材料,是用于传输和分配电能的电缆,电力电缆常用于城市地下电网、发电站引出线路、工矿企业内部供电及过江海水下输电线。随着中国经济的持续快速发展,电力建设发展迅速,而在电力线路中,电缆所占比重正逐渐增加,而电缆原材料价格较高,每年在电缆的使用上耗资很大。电缆在使用时,要先切割成要求的规格,由于所需规格不同,切割时易产生资源浪费问题。因此,需要开发一种电缆优化分割系统来减少资源的浪费。
电缆的优化分割属于一维下料问题[1-3],近年来,在一维下料问题的研究算法上有了很大的发展,包括线性规划算法[4-5]、启发式算法[6-8]、遗传算法[9-11]、蚁群算法[12]等,而研究内容大多是单一规格的下料问题。近年来遗传算法发展很快,是目前发展比较完善的一种优化算法,可以很好地解决小规模以及大规模一维下料问题。因此,本文采用遗传算法来研究多规格一维下料问题,并且应用MATLAB与Microsoft Visual Studio 2010(VS)两种工具来实现电缆优化分割系统。
1 数学模型的建立
根据原材料的类型,一维下料问题可以分为单一规格(原材料的长度相等)一维下料问题和多规格(原材料长度不同)一维下料问题;根据原材料的数量,可以分为完全下料(原材料的数量足够,可得到所有需求型材)和不完全下料(原材料数量有限,只能得到部分需求型材)问题。本文主要研究多规格完全一维下料问题。
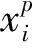
本文要达到的目标是使电缆原材料的使用量达到最小,建立数学模型如下所示:
目标函数:
(1)
约束条件:
式中:N是正整数;F是原材料的使用量;p是第j种原材料下料方案的数量。
2 遗传算法设计
2.1 遗传算法原理
遗传算法是模拟生物在自然环境下的遗传和进化过程而形成的一种自适应全局优化概率搜索方法。采纳了自然进化模型,从代表问题可能潜在解集的一个种群开始,种群由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体,初始种群产生后,按照适者生存和优胜劣汰原理,逐代演化产生出越来越好的解。
2.2 编码方法
本文研究的是多规格原材料一维下料问题,由于原材料的长度不同,不能按照一般遗传算法编码方式进行编码,因为在后续进化过程中,经过交叉、变异,不能确定所得需求电缆对应哪一种长度的原材料。考虑到建立的数学模型以及实际的下料情况,本文应用一种类似于实数编码的方法,个体的长度即为所有需求电缆的数量和,假设所有原材料都参与计算,给所有规格的原材料逐一进行编号,之后将上述编号随机给个体赋值,即完成编码。这种编码方法涵盖了模型里面的三个约束条件:下料使用的原材料数量不多于对应库存电缆原材料的数量;对相应原材料进行切割,最后得到的下料方案里面,各需求电缆的数量与实际需要的数量相等;决策变量均为整数。
2.3 适应度函数
应用遗传算法求解问题时,常用适应度函数来对结果进行判断,适应度值越大则表示得到的结果质量越好。由于目标函数是使原材料的使用量最小,可考虑采用原材料使用量的倒数为适应度函数,不过这样会使适应度值很小,很难做出其他方面的判断。比如,由于个体是随机编码实现的,有可能会出现过多需求电缆集中到某一根原材料甚至超出其长度的情况,即产生不可行解的情况,为了减少以上情况的发生,将原材料的利用率设置为适应度函数:
(3)
适应度值最大为1,也就是原材料全部应用与需求电缆的情况。
然而,当出现适应度值大于1的情况时,也就是出现不可行解时,为了防止对计算结果产生较大的影响,需要对适应度设置惩罚机制,引入罚函数,设计如下:
(4)
2.4 遗传算子
(1)选择算子
选择的标准一般是按照适应度来进行的。初始种群规模设置为N,个体在经过交叉、变异之后,会得到两个下一代,由于得到的两个子代是具有一定随机性的,因此得到的两个子代质量不一定高于上一代,也不一定会符合约束条件。为了得到最优的子代,使种群得以进化,所以要对两个子代以及上一代种群进行选择。
三代种群中,对于不符合约束条件的个体进行惩罚,即采用对适应度设置的惩罚机制进行处理。将三代个体按照适应度从大到小的顺序进行排列,将排在前面的N个个体作为父辈种群进入下一轮的进化。
(2)交叉算子
交叉算子在后代进化过程中起主要作用,将交叉概率pc设置为0.85,采用单点交叉算子完成个体的交叉。首先将上一步得到的父辈群体按照优劣顺序两两进行交叉,假设已确定进行交叉的两个个体为X1、X2,个体的交叉点位置P随机确定,之后个体X1得到P1、P2两个分段,个体X2得到M1、M2两个分段,将P1、M1分段进行交换,得到交叉后个体。计算得到新个体的适应度,如果适应度的值大于1,或者说该个体不满足约束条件,则返回交叉前的个体,重新确定交叉点位置进行交叉。
(3)变异算子
在遗传进化过程中,会发生一些突变,尽管突变得到的基因有好有坏,但这些突变在遗传的进化过程中是起到很大作用的。在种群的进化过程中,引入变异算子。设置种群的变异率pm为0.05,上一步交叉后得到新的种群,通过种群的变异率随机得到变异的个体,对相应个体随机确定两点M1、M2,将M1、M2进行交换得到新的个体。由于变异具有随机性,无法确定新个体的质量,同样计算得到新个体的适应度,如果适应度的值大于1,或者说该个体不满足约束条件,则返回变异前的个体,重新确定变异位置进行变异。
2.5 算法流程
具体算法流程如下:
Step1 种群初始化:确定编码机制,以及种群规模N,得到初始种群。
Step2 适应度函数:根据建立的数学模型,确定适应度函数。
Step3 交叉:随机确定交叉个体,采用单点交叉的方式,得到新的种群。
Step4 变异:随机确定变异个体,得到变异后种群。
Step5 选择:从种群中选择适应度值最大的N个个体,得到新的种群。
Step6 判断:满足判断条件,输出最优解;否则,转到step3。
Step7 算法结束。
3 电缆优化分割系统的设计与实现
3.1 优化算法的调用
系统通过MATLAB与VS工具混合编写程序实现,其中核心算法的实现由MATLAB完成的,电缆相关数据的输入部分,即系统的实现是由VS完成的。根据上一章确定的算法流程,应用MATLAB编写程序,核心算法编写完成后,继续应用MATLAB工具将程序生成动态链接库,即dll文件,为VS工具的调用做好准备工作。
3.2 系统的流程设计
系统流程如图1所示。
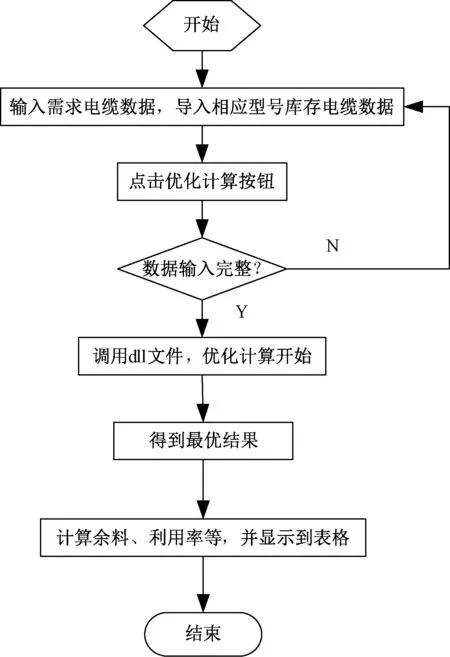
图1 软件优化计算流程图
系统主要包括电缆库存管理和优化计算两部分。库存管理主要包括电缆原材料的添加、修改、删除等,后台连接的是Access数据库,实现对电缆原材料库存的管理与保存,在优化分割系统中加入库存管理功能,避免了用户在每次使用前对于电缆原材料的手动输入,减少了用户的工作量,在一定程度上方便了用户的使用。优化计算部分主要包括需求电缆数据的输入、对应型号电缆原材料的导入、优化计算以及结果的输出等。
3.3 系统主界面设计
系统主界面设计如图2所示。
界面右侧添加了选项卡,内容分别为库存管理、优化结果以及库存统计。打开主界面,系统右侧选项卡部分显示的是库存管理界面,系统连接Access数据库,准确显示出库存电缆的基本信息。系统左侧表格是需求电缆信息的输入位置,计算前根据实际需要输入需求电缆信息,然后在界面中间的库存电缆信息位置选择对应型号的库存电缆,导入数据,点击优化计算按钮,完成计算。
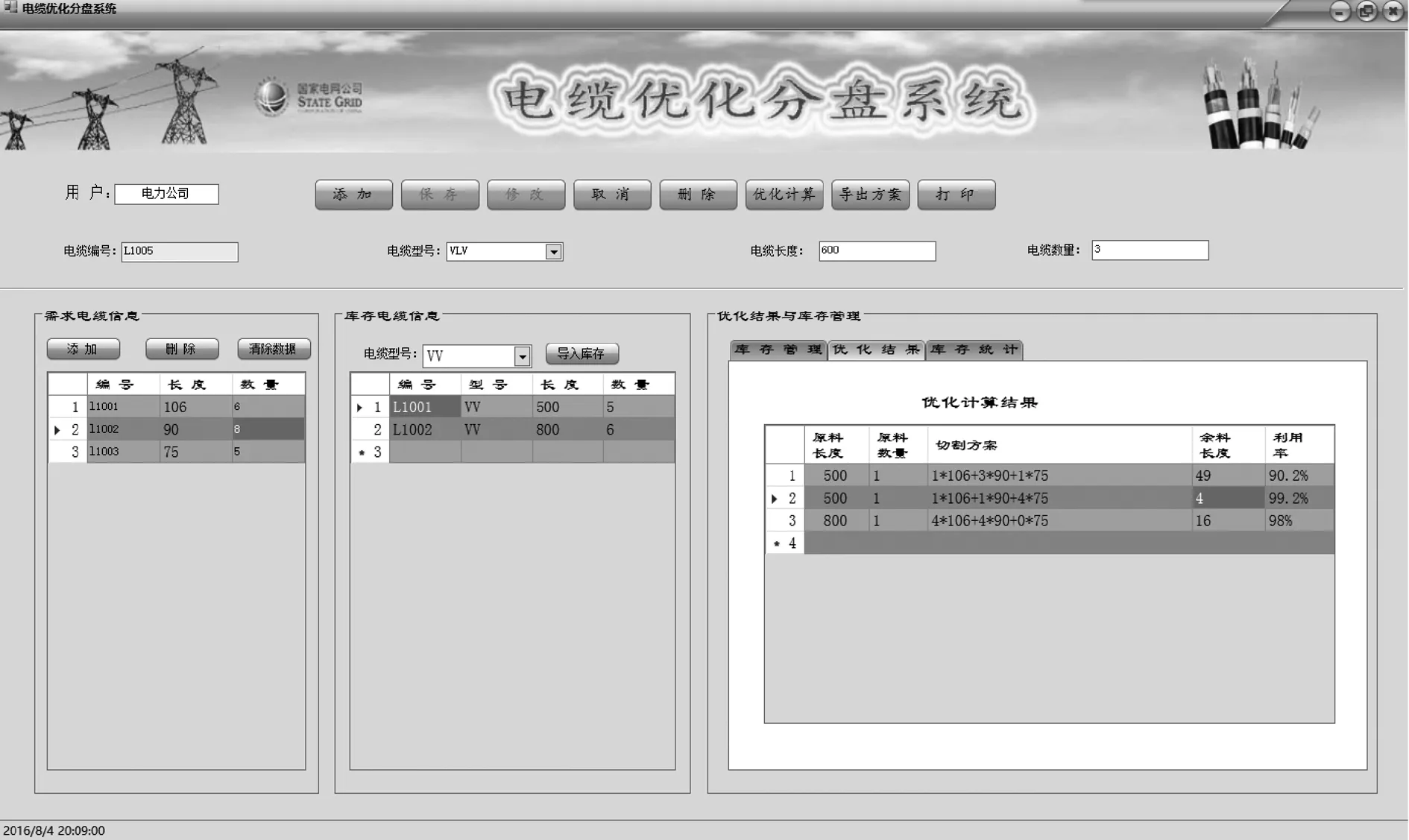
图2 软件界面图
3.4 系统运算实例
(1)小规模问题
某电力工程建设需要一定数目的电缆,其中对应型号电缆的库存原材料为500 m的电缆原材料3轴,800 m的电缆原材料2轴,其中需求电缆的信息如表1所示。

表1 需求电缆信息
应用电缆优化分割系统的计算平台,输入需求电缆基本信息,导入对应库存电缆信息,点击优化计算按钮,计算完毕后,结果将显示在主界面的优化结果表格中。通过优化计算,得到原材料的下料方案,结果如表2所示。共三种下料方式,优化结果与电缆需求一致,不需要对优化结果进行后续的处理,操作简单、准确。

表2 遗传算法优化结果
表3为经过线性规划算法得到的优化结果,由于应用的线性规划是将所有优化下料方案优化组合,从而得到最优结果,运算速度较慢,而需求电缆数量固定,通过组合会出现无解的情况,出现这种情况时需将约束范围扩大,得到如表3所示的近似最优解。从中可以看出计算得到的方案与需求并非完全相符,之后需要进一步的优化,较为繁琐。
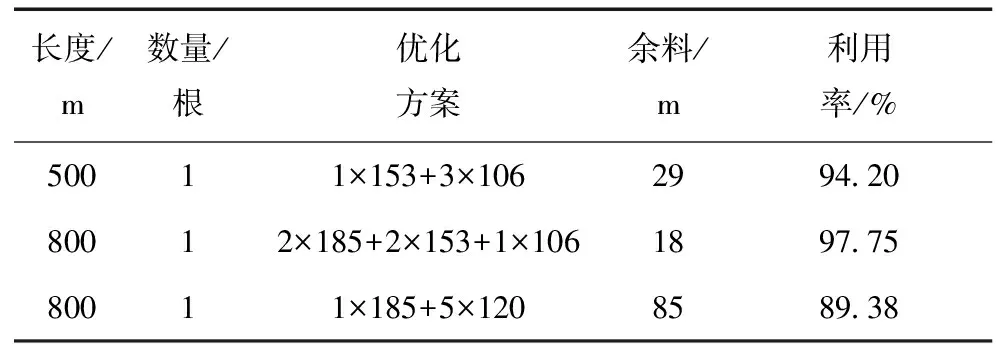
表3 线性规划优化结果
通过以上两种算法的对比,可以看出系统运算速度快,操作简单,得到的优化结果与电缆需求保持一致,电缆原材料利用率高,质量较好。
(2)大规模问题
某电力工程建设需要一定数目的电缆,其中对应型号电缆的库存原材料的长度分别为1 200 m、1 100 m、1 000 m、800 m、700 m、600 m、500 m,对应库存数量依次为2轴、3轴、5轴、3轴、1轴、3轴、2轴。需求电缆的信息如表4所示。
应用电缆优化分割系统的计算平台,输入需求电缆基本信息,导入对应库存电缆信息,优化计算完毕后,得到结果如表5所示。
对于数据较多的大规模问题,每种原材料对应的下料方案过多,应用线性规划算法运算速度较慢,很难得到最优方案。表5为应用电缆优化分割系统得到的优化结果,优化后下料方案与需求电缆信息一致,质量较好,说明系统在处理数据较多的问题时是可行的。

表4 电缆原材料库存信息
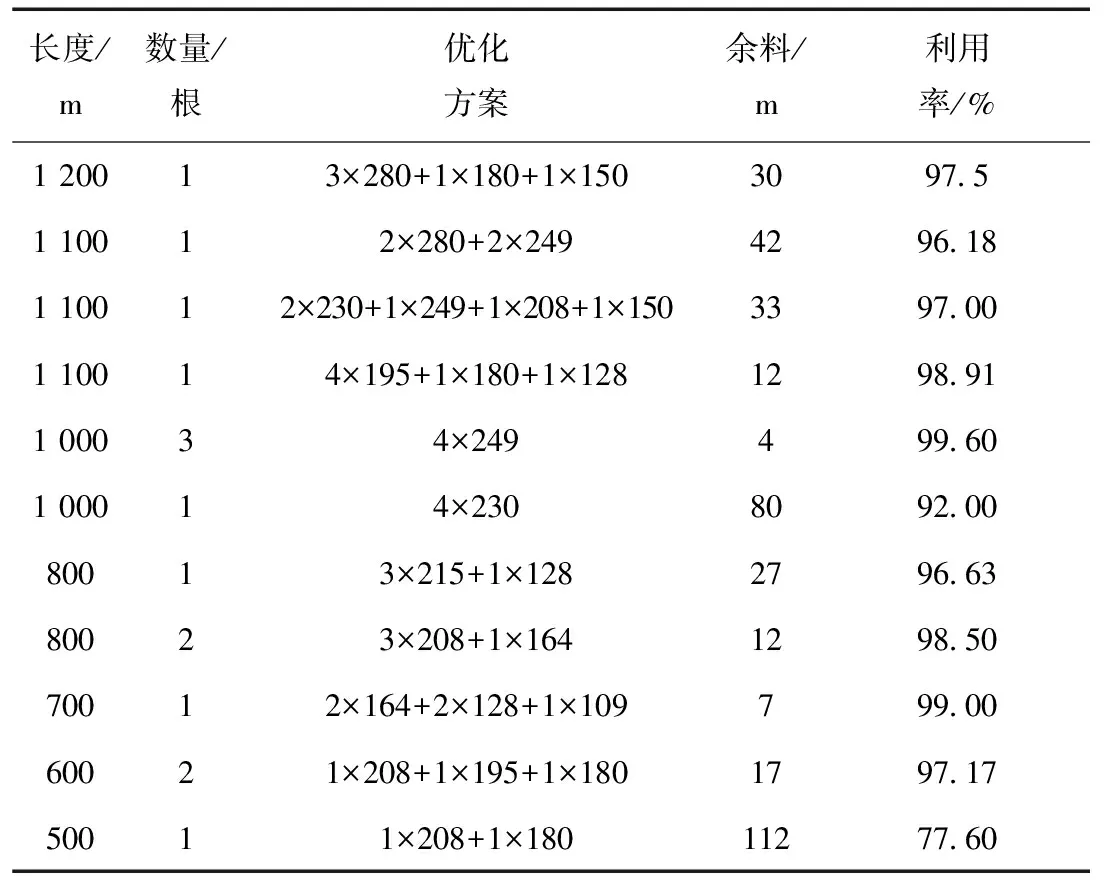
表5 优化计算结果
4 结论
以电缆原材料编号的一种随机排列为一个个体,其中每个编号就代表着一个基因,基因数量设置为需求电缆的总数量。进化过程中,通过选择、交叉、变异,一步步得到近似最优解。系统软件部分由VS工具编写,调用核心算法,实际应用中计算速度较快,并且通过在软件中的进一步计算、整理,可以得到电缆分割的最优下料方案。
系统操作简单、方便,运算速度较快,可以得到质量较好的优化方案,较好地解决了多规格一维下料问题,也在一定程度上方便了对电缆原材料库存的管理。
[1] 崔耀东,周密,杨柳.多线材一维下料问题的求解策略[J].广西师范大学学报(自然科学版),2012,30(3):149-153.
[2]刘林,葛菲菲,刘心报.多目标一维下料决策方法研究[J].中国机械工程,2013,24(7): 951-955,963.
[3]王小东,李刚,欧宗瑛.一维下料优化的一种新算法[J].大连理工大学学报,2004,44(3):407-411.
[4]LEE J.In situ column generation for a cutting Stock problem[J].Computers & Operations Research,2007,34(8):2345-2358.
[5]万书亭,韩国栋.MATLAB与C#.net混合编程的电缆优化分割研究[J].中国电力,2013,46(6):48-51.
[6]方昶,刘心报,裴军,等.基于顺序启发式进化算法的多目标一维下料问题[J].中国管理科学,2012(s1): 94-100.
[7]祝胜兰,饶运清.一维下料问题的启发式方法[J].机械制造与自动化,2014,43(1):52-55.
[8]程浩,刘心报,方昶.基于混合顺序启发式算法的一维下料问题[J].中国机械工程,2014(16):2191-2195,2203.
[9]王晓伟,刘林,周谧.蜂群遗传算法在一维下料问题中的应用[J].微型机与应用,2012,31(6):66-68,71.
[10]寿周翔,王琦晖,王李冬,等.一维下料的改进遗传算法优化[J].计算机时代,2014(1):36-37,41.
[11]李斌,贺飞.求解一维下料问题的改进混合遗传算法[J].内蒙古大学学报(自然科学版),2014,45(3):245-250.
[12]徐平平,郭蕴华.基于改进蚁群算法的不定长原管一维下料废料率优化[J].船海工程,2016,45(1):113-116.
Research and Development of Optimal Cutting System of Cable Based on Genetic Algorithm
LIU Ya1,LI Shenghua2,YUAN Li2,WAN Shuting1
(1.School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003,China; 2.State Grid Taizhou Power Supply Company, Taizhou 225300,China)
The optimal cutting problem of the power cable belongs to the one-dimensional cutting stock field. A new method based on the genetic algorithm is proposed to solve the problem of one-dimensional cutting stock with multi dimensions. The cable material uses a sequential numbers as an individual identification. Each of these numbers represents a gene. The number of genes is equal to the number of the demanded cables. At the same time, the fitness function is determined according to the established mathematical model. In the process of population evolution, the fitness function is used for evaluation, and the optimal solution is obtained by selecting, crossing and mutating. The algorithm of the system is realized by MATLAB tool, and the interface is realized by VS tool. Through two kinds of tools, the preparation of the software is achieved. The experimental results show that the system calculation speed is fastened, and it can solve the problem of optimal cutting of the cable.
cable; optimal cutting; one-dimensional cutting stock; genetic algorithm
10.3969/j.ISSN.1672-0792.2017.03.003
2016-09-12。
国家自然科学基金(51177046);河北省自然科学基金(E2015502008)。
TM757
A
1672-0792(2017)03-0013-05
刘亚(1990-),女,硕士研究生,研究方向为电力设备优化理论及应用。
