家庭需求侧资源与电力供应商双向交互策略

叶中行，孙明远

(长沙理工大学电气与信息工程学院，湖南长沙410114)

家庭需求侧资源与电力供应商双向交互策略

叶中行，孙明远

(长沙理工大学电气与信息工程学院，湖南长沙410114)

需求侧资源参与到家庭与电力供应商之间的能量交换过程,能够降低自身用电成本。针对可平移负荷不同用电特点进行综合建模，结合电动汽车、光伏，小微储能装置模型提出新的家庭需求侧资源与电网的双向能量交换模型，通过求解该模型，对比分析了在需求侧资源中加入可平移负荷前、后所得的调度结果，负荷平移后，家庭电费明显降低，且起到了削峰填谷的作用；讨论了需求侧资源与家庭和电网之间单向与双向交互模式下的经济效益，得出了智能家庭最优调度策略，为进一步的家庭实践打下基础。

需求侧资源；优化；可平移负荷；对比分析

0 引言

随着电力市场化进程的加快，家庭用户作为独立的个体参与到电力能源优化配置过程，与电力供应商进行互动交易逐渐受到人们的关注[1]。因此，家庭能量管理系统(Home Energy Management System，HEMS)应运而生，该系统以实时电价为参考，以需求侧资源[2](Demand Side Resources, DSR)为调度目标，以经济、舒适为原则，合理安排负荷用电区间。

经济、社会的发展，使越来越多的家庭有能力构建以小微储能装置(ESS)、电动汽车(EV)、分布式光伏(PV)等需求侧资源为要素的家庭能量体系[3]。可以通过与电网的电能交互产生一定收益，从而有效减少用户电费成本，同时对电网来讲也能起到削峰填谷之用[4-5]。

国内外已经有相关的研究并用于生产实际，从需求侧资源的响应、调度、控制策略以及优化调度算法方面做了大量的工作。文献[3-6]建立了包含各种家电模型的智能家庭用电协同调度策略；文献[1]基于负荷资源分类建模，利用启发式算法对模型进行求解；文献[4]建立了电动汽车与家庭互动调度模型，并提出了新的智能算法；文献[5]采用MPC方法建立家庭能源局域网能量管理模型，并以电价预测为基础寻求最优调度方法。上述文献对于家庭能量优化管理的研究，虽考虑了需求侧资源对调度结果的影响，但并没有对一类负荷进行具体建模，而且对需求侧资源与家庭或外电网的交互考虑的不够。文献[7-8]虽然考虑了负荷建模，但研究的是微网的运行优化问题。

本文基于需求侧响应(DSM)，针对不同负荷的用电规律提出可平移负荷模型，在实时电价的基础上优化用电时段；以用户电费最小为目标，构建考虑DSR与家庭、电网间双向交互形式下的家庭能量优化管理模型；通过算例仿真，对比分析了负荷平移对家庭能量优化调度结果的影响以及各种交互形式下的电费成本，验证了所提模型的有效性。

1 可平移负荷模型

1.1 目标函数

本文中负荷平移的目标是将可平移负荷从电价高峰时段转移到电价低谷时段，从而通过该电价差达到削减用户电费的目的[6-7]，其目标函数表达式为：

(1)

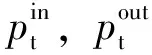
(2)

(3)

式中：第一项考虑在负荷运行的第一时段转入的总功率，该总功率也包括横跨多个运行时段的负荷类型；第二项考虑的是多时段运行负荷转入的后续功率；m1为可平移负荷种类总数；m2为运行时段数大于1的负荷总类数；xk,i,t表示从i时段转入至t时段的第k类负荷数；xk,t,q表示从t时段转出至q时段的第k类负荷数；hmax≥2为负荷持续运行时段数的最大值；p1,k为第k类负荷在其第1个运行时段的功率；ph+1,k为第k类负荷在其持续运行时段内第h+1运行时段的功率。

1.2 约束条件

(1)延迟时段约束

(4)

通常规定用电设备用电时段只能延迟，而不能提前[9]，最大延迟时段为dmax。

(2)负荷平移量约束

根据可平移负荷特点必须保证平移前后同一类别的负荷单元数量维持不变

(5)

式中：xk,t为负荷平移前第k类负荷在t时段的负荷单元数量。

(3)在每一住宅单元每一用电时段通常会有一个限制总能量，一方面限制电网峰值功率，一方面可以间接起到削峰填谷的作用[10]，表达如下：

(6)

式中：pt,after为负荷平移后时段t的功率；pmax为每时段统一的限制功率。

2 智能家庭能量管理优化建模

2.1 智能家庭能量管理目标函数

通过各需求侧资源的实时调度，实现智能家庭电费最小这一目标，该目标由家庭向电网的买电成本与卖电收益两部分构成，其表达式为：

(7)

式中：pt,g为t时段电网向家庭输送的功率；pt,s为t时段电网向家庭购入的功率，这部分功率由EV、ESS、PV提供，暂不计及各设备向电网的卖电顺序；λt,b,λt,s均为实时电价[10]。

且式(5)满足以下约束条件：

(8)

(9)

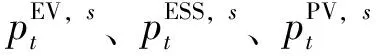
2.2 需求侧资源模型

考虑到各需求侧资源与电网、家庭之间的双向功率交换，每一时段都有发生各种功率交换方式的可能，基于此，建立模型如下：

(1)电动汽车模型

(10)

(11)

(12)

式(10)～(12)均∀t∈[ta，td]

SEV(t)为EV在t时段的荷电状态，其满足如下约束：

(13)

(14)

(15)

(16)

(17)

(18)

式(13)表示SEV(t)在每一时段的状态值表达式；式(14)表示状态变量界限；式(15)(16)表示必须充满电与必须释放完的两种极限状态；tf,c为必须充满的时刻；tf,d为必须释放完的时刻；式(17)表示EV到家时的荷电状态等于其初始值；式(18)表示EV在离开家后并无任何意义。

(2) 储能单元模型

(19)

(20)

(21)

(22)

(23)

(24)

(3)家庭分布式光伏模型

(25)

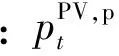
(4)实时功率平衡

负荷平移后的负荷分布势必会对调度结果产生重要影响，鉴于此，本文将实时功率平衡分为负荷平移前、后的功率平衡

①负荷平移前实时功率平衡

(26)

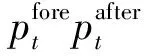
②负荷平移后实时功率平衡

(27)

3 数值实验

3.1 算例系统

为验证上文所提出的模型的有效性与实用性，以引入可平移负荷前、后的两个不同家庭能量管理系统进行对比分析。家庭EV和ESS、PV各相关参数[11]如表1所示；PV出力预测数据如图1[15]；EV荷电状态上、下限分别为18 kW、4.8 kW；ESS荷电状态上、下限为1 kW、0.25 kW；电网向家庭购入电能上限为1 kW·h，价格设为定值0.6元/kW·h；电网向家庭输送电能上限为2 kW·h。

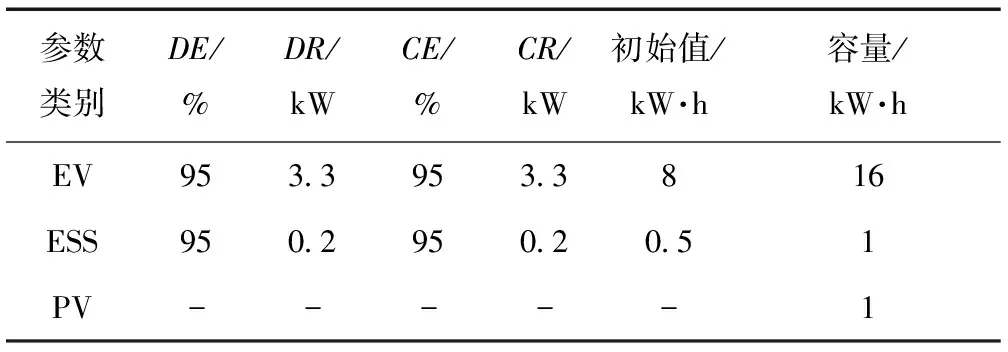
表1 相关参数

选取3类可平移负荷参与计算，分别是消毒柜、洗衣机和电热水器[12]。消毒柜持续运行时间为1 h，功率为0.7 kW；洗衣机持续运行时间为2 h，功率分别为0.4 kW和0.25 kW；电热水器持续工作时间为3 h，功率分别为2、1.5、1.2 kW；家庭负荷的预测功率[16]如图2。

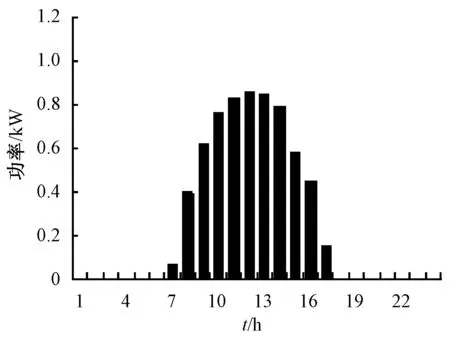
图1 PV出力柱状图

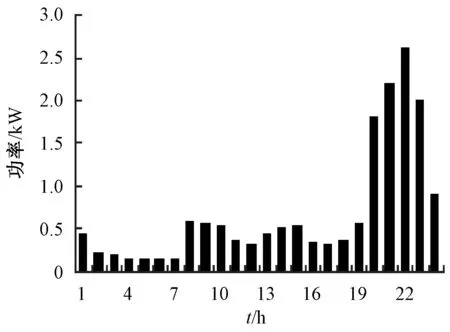
图2 家庭负荷预测功率柱状图

在频率为2.3 GHz的PC上运用lingo建模软件运用分支定界算法进行仿真计算，选取调度周期为一天，分为24时段，调度时段从00:00到24:00。

3.2 负荷平移前、后调度结果分析

3.2.1 需求侧调度结果

考虑到负荷平移前EV、ESS、PV与电网和家庭之间的双向交互，有必要对负荷平移前的调度结果进行分析研究，以预测负荷和平移后负荷作为负荷输入，其调度结果如图3、4所示。

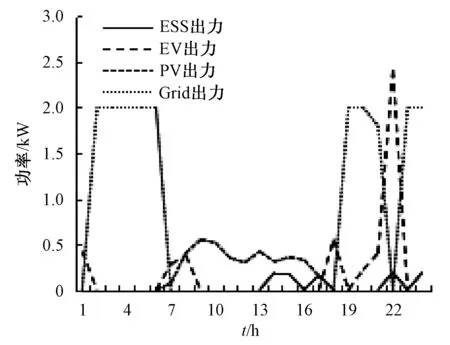
图3 负荷平移前调度结果

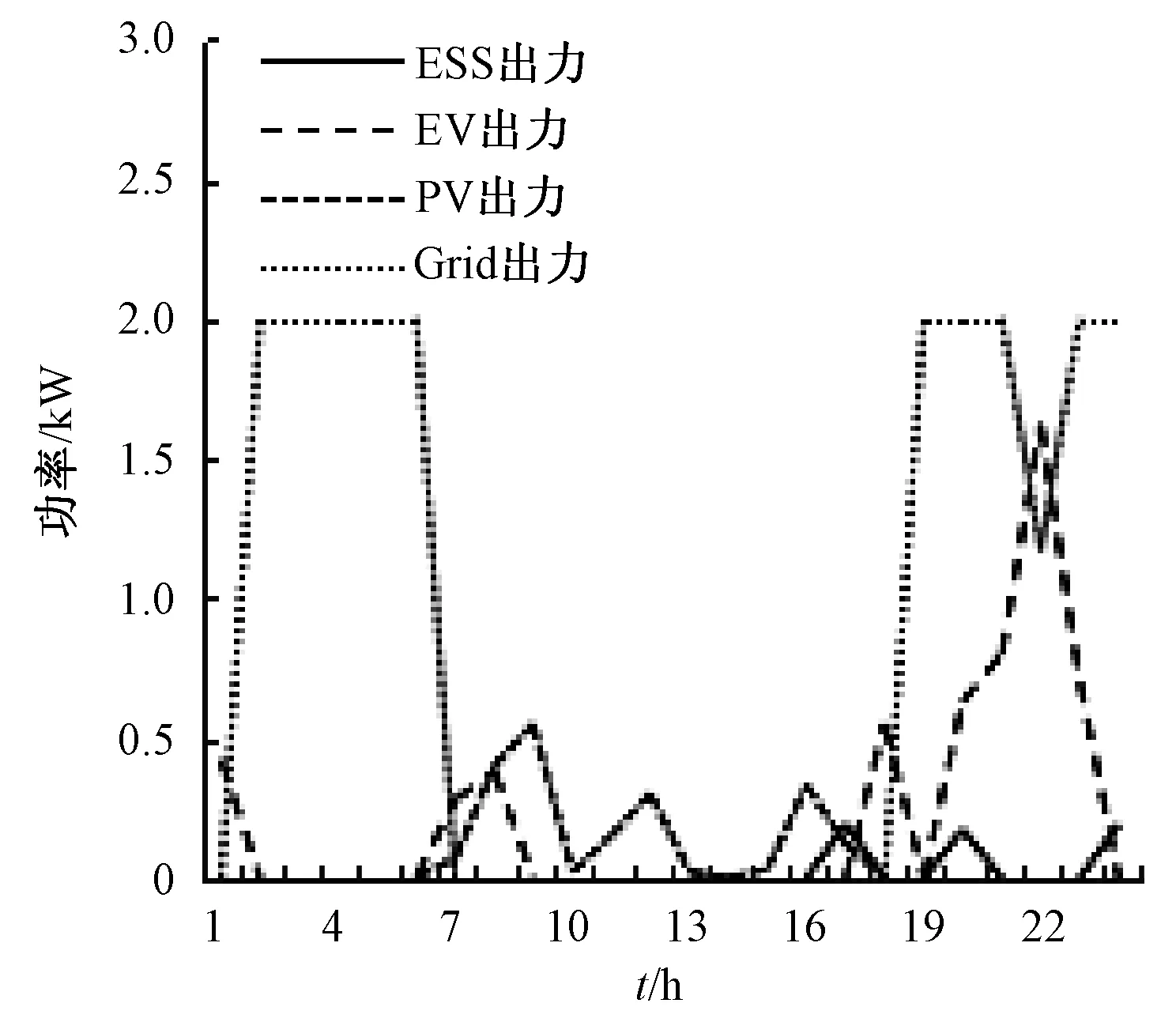
图4 负荷平移后调度结果

在图3不难看出，在夜间电网电价较低的时候Grid出力始终维持在较高水平，而在白天则主要依靠PV和ESS所提供的电能；在夜间则是电网与EV共同发力，维持负荷运行。

图4在实施负荷平移后，夜间EV出力尖峰有着明显下降，且同一时刻的电网出力相对有所回升，进一步说明负荷平移起到了削峰填谷的作用。

图5反映了未考虑DSR响应情况下的负荷平移前、后其与实时电价之间的关系，可以看出平移后的负荷变化与实时电价密切相关，夜间电价低谷时负荷明显上升，达到了2.8 kW，而时段1～6在负荷平移前、后曲线几乎是重合的，而在后续时段出现了急剧上升为1.23 kW，这就是负荷平移的结果。

图5 负荷平移结果

3.2.2 功率平衡调度结果

图6和图7分别为负荷平移前、后功率平衡调度结果，其中图6设定了时段负荷限值为2.8 kW，可以看出在1～6时段电网真正提供给负荷的功率很小，绝大部分被EV或ESS吸收了，因为此时正处在电价低谷时段，且在1时段EV还向电网售出了部分功率；而在7～17时段，PV与ESS一起参与负荷供能；而在夜间负荷上升，则主要由电网与EV联合进行供电，且没有超过其峰荷限值。

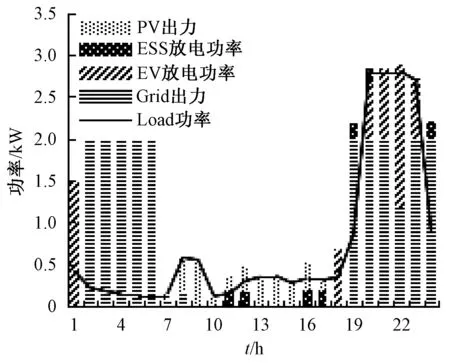
图6 负荷平移后功率平衡调度结果

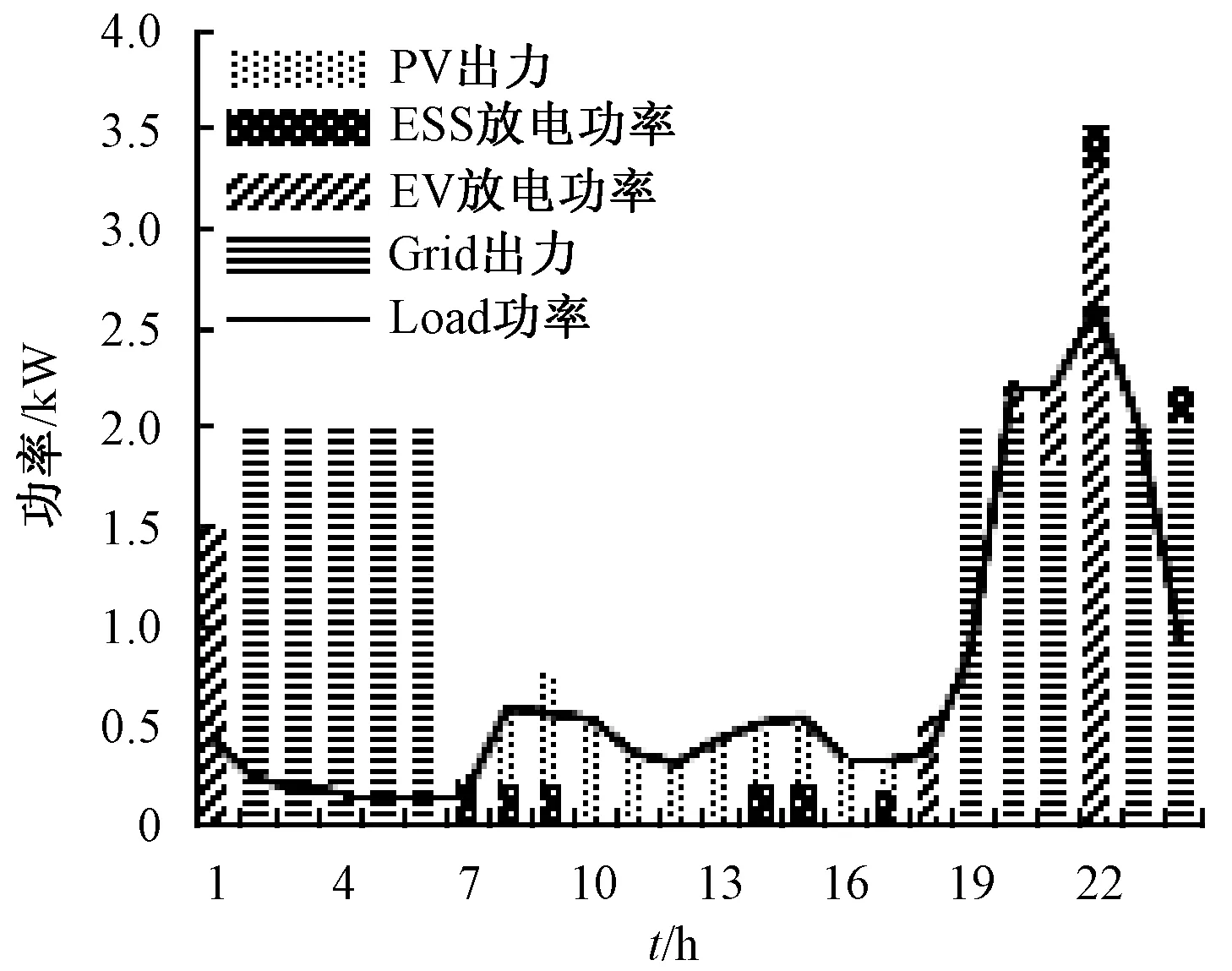
图7 负荷平移前功率平衡调度结果

平移后负荷曲线在夜间出现了一段持续高峰，比负荷平移前多出了一些，这是由于负荷已经转移到这一用电区域。

3.3 不同节电模式对优化结果的影响

本文设置基准节电模式，即在加入可平移负荷之前EV、ESS、PV与家庭、电网间的双向交互模式，其他模式均为在此基准模式上衍生而出的。得到目标结果如表2所示。

表2 不同模式下优化结果

由上表看出，模式1与模式2对比，一旦不考虑V2G，用户电费急剧增大了2.1元；模式3与模式1对比，则说明通过负荷转移，使电费下降了1.43元；模式4与模式2对比，则减少了1.49元；模式4与模式3对比，电费增大了2.01元，表明V2G与负荷转移的巨大作用。

4 结论

本文从需求侧出发，引入负荷控制，对家庭能量的优化调度问题进行了研究。对需求侧资源进行分类建模，综合考虑V2H、V2G和ESS2H、ESS2G模式下的家庭能量优化调度问题，并在此基础上建立和引入可平移负荷模型，建立了考虑负荷平移的混合整数线性规划模型，利用lingo优化软件对模型进行求解。由仿真结果分析可知：

(1)在实时电价的作用下，负荷平移确能起到削峰填谷的作用，其不仅能够应用于家庭网络，也同样适用于其他大型电网。

(2)实施负荷平移，能够大大节省用户电费。

(3)以需求侧资源为媒介与电网进行互动交易，能够使家庭能源利用效率更高，更具经济性。

可以在家庭与电网之间引进可中断负荷合同，从而进一步优化家庭用电结构。

[1]于雷，汤庆峰，张建华.基于负荷资源分类建模和启发式策略的家居型微网优化运行[J].电网技术，2015,39(8):2180-2187.

[2]邢龙,张沛超,方陈,等.基于广义需求侧资源的微网运行优化[J].电力系统自动化,2013,37(12):7-12,133.

[3]王守相,孙智卿,刘喆.面向智能用电的家庭能量协同调度策略[J].电力系统自动化,2015,39(17):108-113.

[4]黄宇,杨健维,何正友.基于双层离散粒子群优化的智能小区车辆与家庭互动调度策略[J].电网技术,2015,39(10):2690-2696.

[5]张彦,张涛,刘亚杰，等.基于模型预测控制的家庭能源局域网最优能量管理研究[J].中国电机工程学报,2015,35(14):3656-3666.

[6]刘经浩,贺蓉,李仁发,等.一种基于实时电价的HEMS家电最优调度方法[J].计算机应用研究,2015,32(1):132-137,160.

[7]林弘宇,田世明.智能电网条件下的智能小区关键技术[J].电网技术,2011,35(12):1-7.

[8]符杨,蒋一鎏,李振坤,等.计及可平移负荷的微网经济优化调度[J].中国电机工程学报,2014,34(16):2612-2620.

[9]LOGENTHIRAN T,SRINIVASAN D,SHUN T Z. Demand side management insmart grid using heuristic optimization[J]. IEEE Transactions on Smart Grid,2012,3(3):1244-1252.

[10]BRUSCO G,BURGIO A,MENNITI D,et al.Energy management system for an energy district with demand response availability[J]. IEEE Transactions on Smart Grid,2014,5(5):2385-2393.

[11]ERDINC O,PATERAKIN.D.Smart household operation considering bi-directional EV and ESS utilization by real-time pricing-based DR[J].Smart Grid IEEE Transactions on,2015,6(3):1281-1291.

[12]韩伟强,王贵斌,文福拴.电动汽车充电设施多阶段最优规划[J].华北电力大学学报(自然科学版),2014,41(5):23-30.

[13]刘青,樊世通.考虑蓄电池极化效应的储能容量配置方案研究[J].电力科学与工程,2015,31(7):1-5.

[14]周念成，邓浩，王强钢，等.光伏与微型燃气轮机混合微网能量管理研究[J].电工技术学报，2012，27(1)：74-84.

[15]罗振宇,陈家俊,周勇.等考虑负荷不确定性的分布式电源的长期优化配置[J].电力科学与工程,2014,30(12):61-67.

[16]程晓悦,卢锦玲.考虑不确定性的分布式电源多目标优化配置[J].电力科学与工程,2014,30(11):16-21.

Bi-directional Interaction Strategy Household Between Demand Side Resource and the Electricity Supplier

YE Zhonghang, SUN Mingyuan

(College of Electrical and Information Engineering,Changsha University of Science and Technology, Changsha 410004,China)

The cost of electricity consumption could be reduced with the demand side resources involving in the energy exchange process between the demand side and power suppliers. The integrated model is built in the light of the electricity consumption features of the shiftable load, which is the combination of the electric vehicles, photovoltaic, small and micro energy storage device. The newly proposed two-way exchange model between household demand side resources and grid can be solved, and comparative analysis of scheduling results that before and after shiftable load being added in the demand side resources is conducted. After the load shift, the household electricity fees are obviously cut down, and the peak shaving effect manifests itself. The economic benefit produced by the interactive mode of the demand side resources, family and the grid, unilaterally and bilaterally, is analyzed in this paper. The optimal scheduling strategy of intelligent home has drawn according to the research findings. Solid foundation has been laid for further family practice.

demand side resources; optimization; shiftable load; comparative analysis

10.3969/j.ISSN.1672-0792.2017.03.001

2016-09-05。

国家自然科学基金(11171095)。

TM711

A

1672-0792(2017)03-0001-06

叶中行(1992-)，男，硕士研究生，研究方向为电力系统分析、能量优化调度。