电网数据可信性度量模型研究
2017-04-21程晓荣李天琦
程晓荣,李天琦
(1.华北电力大学 控制与计算机工程学院, 河北 保定 071003)
电网数据可信性度量模型研究
程晓荣,李天琦
(1.华北电力大学 控制与计算机工程学院, 河北 保定 071003)
针对电力系统中不可信数据将导致电力系统状态估计结果的准确性降低,分析了电网中数据的可信性需求,研究了电力系统不良数据的辨识和数据可信分析理论,构建了层次化、动态化的电网数据可信分析模型。该模型引入时间因子、惩罚因子等权重参数,将电力数据的可信性分析问题归结为数据源、数据源之间及数据传播网络路径的组合问题,即通过计算数据源之间的可信度、数据源的可信度、数据的可信度,动态地构建了基于数据源依赖关系的可信虚拟网络,最后通过所构建的可信虚拟网络来评估出电力数据的可信度。仿真实验结果表明,该模型能较好地满足电网数据的可信性评估需求,为可信性评估方法进一步研究提供了解决思路。
电网数据;大数据;可信度;动态性;可信计算
0 引 言
目前,在智能电网系统中,大数据贯穿于发电、输电、变电、配电、用电、调度等电力生产及管理的各个环节[1],与此同时,电力系统发展速度越来越快,网络的结构、运行模式也变得越来越复杂。电力大数据具有典型的“3V”和“3E”特征,即:体量大(Volume)、速度快(Velocity)、类型多(Variety)和数据即能量(Energy)、数据即交互(Exchange)、数据即共情(Empathy),同时从特征中不难发现电力数据的典型“HDC”属性,即数据的异构性(Heterogeneous)、动态的数据体系(Dynamic)、数据的复杂性(Complexity)。因此,在电力数据集合中必然充斥着大量不可信的数据[2],这些不可信数据的存在会造成电力系统状态估计的失败,影响调度员做出错误的决策,进而影响智能电网系统的正常运行,甚至可能威胁整个电力系统的安全[3,4]。如果能及时对原始数据进行可信度的评估,那么就会有效降低风险,提高电力数据的可信性。
电力系统不良数据辨识方法一般以加权最小二乘状态估计方法为基础,包括非二次准则法、残差搜索法、零残差法、估计辨识法等,这些方法首先假设测量误差服从正态分布,然后基于假设检验的方法依据残差来辨识不良量测数据。文献[5,6]提出的这些方法容易出现残差污染和残差掩没现象,从而造成漏检或误检,影响辨识的效果。文献[7]运用基于Spark的并行K-means聚类算法提取出日负荷特征曲线,分别对输电网状态估计中的不良数据进行检测和辨识。文献[8]引入基于贝叶斯数据处理策略的扩展卡尔曼滤波算法进行不良数据动态检测。文献[9]利用PMU采集的电压、电流相量,与新息差向量配合使用,提出了使用基尔霍夫电压定律辨识不良数据的方法。基于神经网络的算法由于阈值选取带有很大的主观性和经验性,使得实际应用比较困难,基于模糊理论和聚类分析的算法要求人为的确定隶属度的大小,带有一定的主观性,基于GSA的算法由于算法本身比较复杂,而且要考虑参考分布,当量测数据量比较大时,计算量很大,计算速度会受到影响。若将可信度评估理论应用到不良数据辨识中,进行定量分析,这样就会使得不良数据辨识更加准确。
目前,数据的可信度分析与评估方法主要分为两大类,主观信任分析和客观信任分析,但均不太适应具有“3V”特征的电力数据可信性研究。主观信任分析是基于信念的,一种认知现象,是对信任客体的特定特征或行为的特定级别的主观判断,这种判断相对独立于主体的特征和行为具有模糊性、不确定性,无法精确地描述、验证和推理,文献[10-12]提出了基于概率论、模糊集合理论、云理论等不同的主观信任评估方法。客观信任分析主要是基于证据理论的,通过证据来定义两者之间的信任关系,进行描述、验证和推理,文献[13-16]采用D-S证据理论进行可信度计算。它比主观信任分析更加合理,但并没有考虑时效性及恶意推荐所带来的影响,缺少灵活性。
本文在研究电力系统不良数据的辨识和传统数据可信分析理论基础上,为满足人们对智能电网中的数据可信性和系统运行可靠性的要求,创新性提出了面向智能电网的数据可信性评估模型,给出了一种基于数据源依赖关系的动态化、层次化可信虚拟网络的构建方法。
1 电网数据的可信分析模型
传统的数据可信评估和不良数据辨识的方法虽然在处理小规模数据可信问题时表现出了良好的性能,但是,这些算法均假设所有数据一次性装入内存中,显然无法处理电力大数据,这些方法可处理的数据规模和时效均受到硬件的严重制约。针对电力大数据典型特征和“HDC”属性,本文给出了一种动态构建电网数据可信性度量的模型。本方法采用分布式处理方法,运行在大数据平台上,能有效利用软硬件资源、处理海量增长的电力数据。该模型主要分三部分:数据源之间的可信度量模型、数据源可信度量模型、数据可信度量模型。数据源之间的可信度受数据源的可信度制约,数据源的可信度受数据的可信度和数据源之间的可信度双重制约,数据的可信度受数据源的可信度和数据源之间的可信度双重制约,它们之间相互关联、相互制约,构成一个整体。其关联关系如图1所示。
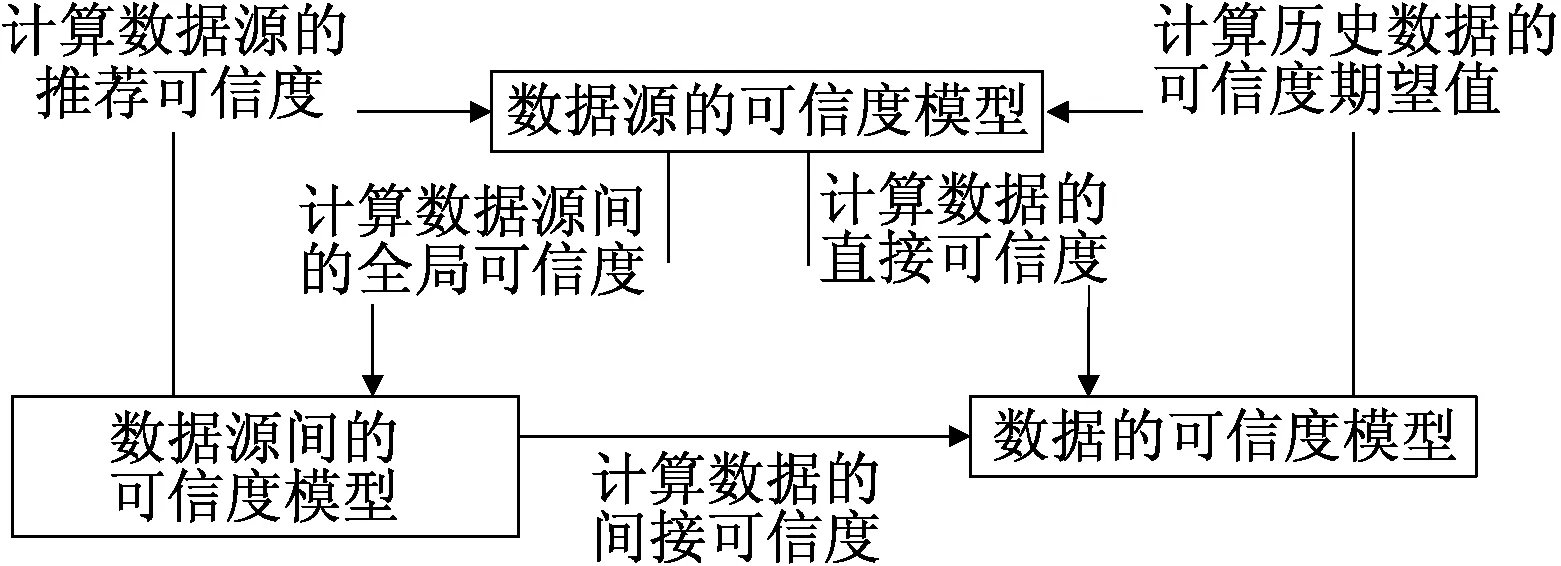
图1 数据源间、数据、数据源的可信度模型关联关系Fig.1 The correlation of the credibility model of between data sources, data, data source
1.1 相关概念
为便于理解,给出本文所提方法的相关定义,来阐述电网数据可信性分析方面的基本问题。
数据源:是指在电网大数据环境下,数据的提供者。
数据:是指由多个属性特征构成。符号记作:data={d1,d2,d3,… ,dn},其中,di是指数据的第i个属性。
可信虚拟网络:是指通过计算数据源之间的可信度而建立的虚拟网络,网络中每个节点相当于一个相应的设备(数据源),网络之间的链接是指数据源之间的可信度值超过一定的阈值而建立的,与具体互联设备构成的网络有所区别。
根据前述对电力数据可信性分析的相关描述,在对电力数据进行可信度计算时,本文给出一种动态的可信性分析网络模型,该模型由层次化的可信虚拟网络结构组成。在初始时刻,该虚拟网络由分散的数据源或专家经验预先得到的数据源构成,且网络拓扑结构是动态变化的;然后,在计算数据源之间的关联可信度时,构建了该模型的可信性分析网络;最后,基于该可信性网络分析模型,进行数据的可信性度量,具体过程如下文所述。
1.2 数据源之间的可信性度量模型
在电网可信度计算过程中,当两个数据源之间有直接的上下文交互或者它们之间所提供的数据或行为的相似度超过一定的阈值时,这时两个数据源之间建立有向链路,随着网络规模的扩大,可信虚拟网络越来越趋于稳定。如果发现某个数据源提供的数据不可信,该模型能很快的对其提供者(数据源)赋以惩罚系数,使得其提供者在一段时间内的可信度降低;但是随着时间的推移,如果数据源能继续提供可靠的数据,那么它的可信度也将会缓慢恢复。在可信性分析网络中,如果数据源之间在一个计算间隔内没有新的上下文直接交互,那么就对其施加一个时间惩罚。
定义1 数据源间的可信度:设TrustA(B,t)表示在t时刻时,本地数据源A对目的数据源B的综合可信度,由数据源之间的本地可信度与全局可信度组合而成,其计算公式为
(1)
式中:α1+β1=1。
定义2 本地可信度:当两个数据源之间有直接的上下文交互或者两个数据源之间所提供的数据或行为的相似度超过一定的阈值时,称此时的数据源之间具有本地可信度。设LocalTrustA(B,t)表示在t时刻时,本地数据源A对目的数据源B的本地可信度,它是由数据源之间直接进行上下文交互的可信度与两个数据源之间的相似度(相似度也可以指相互的认可度)组合而成,其计算公式为
(2)
式中:
(a) 初始值为一个随机数或0,表示数据源A对数据源B有一些信任或没有信任。

(c) ΔContext(A,B,t)表示在t时刻时,数据源A和数据源B之间是否有新增的上下文直接交互。其中,ΔContext(A,B,t)=Context(A,B,t)-Context(A,B,t-1)。
其中,Context(A,B,t)是指在t时刻,数据源A与数据源B之间直接交互数据。
(d)DirTrust(A,B,Context(A,B,t),t)表示在t时刻时,数据源A对数据源B在上下文交互条件Context(A,B,t)下的可信值。
(e)Accept(A,B,t)表示在t时刻时,数据源A对数据源B的相似程度的认可度。

Data(A)∩Data(B)是指数据源A所提供的数据集合与数据源B所提供的数据集合有相同的主题的数据的个数。
(f)λL(t)表示在t时刻时,本模型对本地可信度的惩罚系数。
其中, ΔLocalTrustA(B,t)表示在t时刻时,数据源A对目的数据源B本地可信度是否发生了变化。ΔLocalTrustA(B,t)=LocalTrustA(B,t)-LocalTrustA(B,t-1)。
(g)α2+β2=1。
定义3 全局可信度:设GlobalTrustA(B,t)表示在t时刻时,本地数据源A对目的数据源B的全局可信度,它的值是目的数据源在整个可信虚拟网络中的可信度,即目的数据源的可信度,其计算公式为
(3)
1.3 数据源的可信性度量模型
定义4 数据源的可信度:设Trust(A,t)表示在t时刻,数据源A的可信度,它是指数据源提供的所有历史数据的可信度期望值与整个可信虚拟网络中各层对数据源的推荐可信度的综合可信度。其计算公式为
(4)
式中:
(a) 初始值为一个随机数或0,表示数据源A有一些信任或没有信任。


(d)Trust(dataa,t)表示在t时刻时,对数据dataa的信任度。
(e)Sum(Data(A))表示求数据源A提供数据的总数量。
(f)γn表示在可信虚拟网络中,以所求信任值的数据源为圆心,每一层对目标数据源(圆心数据源)信任权重。它是一个1×n维向量,第一个元素的值为第一层对圆心数据源的信任权重,以此类推,每个向量元素为所对应层次的信任权重,且权重值是个常数,根据专家设定,由内向外逐层递减,取值范围[0,1]之间。
(g)α3+β3=1。
定义5 推荐可信度:设Recommend(A,B,t)表示在t时刻时,数据源A对数据源B以最佳路径得到推荐可信度,它是指本数据源通过最佳路径到目的数据源,对目的数据源的可信度。
设Recommendn(A,t)表示在t时刻时,每层数据源对目标数据源(圆心数据源)A的推荐可信度,其中它是一个n×1维向量,第一个元素的值为第一层所有数据源对目标数据源(圆心数据源)A的推荐可信度期望值,以此类推,每个向量元素为所对应层次的推荐可信度期望值。一般层数是根据精确度和需求设置的,层数越大,计算量越大,相应的得到的数据就越准确。
设Recommend(Xi,A,t)为第i层的某个数据源X对目标数据源(圆心数据源)A的推荐可信度,其计算公式为
(5)
其中,Neighbormax(Xi->A)表示朝向A的方向上,第i-1层上与Xi相邻的可信度最大的数据源。
设Recommend(A,t)(i)为第i层的所有数据源对目标数据源(圆心数据源)A的推荐可信度期望值为
(6)
其中,Circlei(A)表示在可信虚拟网络中,以A为圆心的第i层上的所有数据源,Sum(Circlei(A))表示第i层上的所有数据源的数量。
1.4 数据的可信性度量模型
定义6 数据的可信度:设Trust(data,t)表示在t时刻时,数据data的可信度,它是指对于这条数据,所有的直接提供这条数据的数据源或有直接关系的数据源在历史记录中都提供不可靠数据的对立事件的概率,其计算公式为
(7)
定义7 数据源所提供的某条数据的真实可信度:设Trust(A,data,t)表示在t时刻时,数据源A对所提供的数据data的真实的可信度,它是指由数据源对所有提供数据的直接可信度与间接可信度的综合得到的。其计算公式为
(8)
式中:α4+β4=1。
定义8 某数据源所提供数据的直接可信度:设DirTrust(A,data,t)表示在t时刻,数据源A对所提供的数据data的真实直接可信度,它是指数据源在整个可信虚拟网络中的可信度,其计算公式为
(9)
定义9 某数据源所提供数据的间接可信度:设InDirTrust(A,data,t)表示在t时刻,与数据源A邻接的数据源对这条数据的真实推荐可信度,一般选出有限的n个邻接可信度高的数据源组合成这条数据真实的推荐可信度,其计算公式为
(10)
式中:Neighborn(A)与A相邻的可信度高的n个数据源。
由上面的定义可得数据源间、数据源及数据的可信度定义之间关联关系,如图2所示。
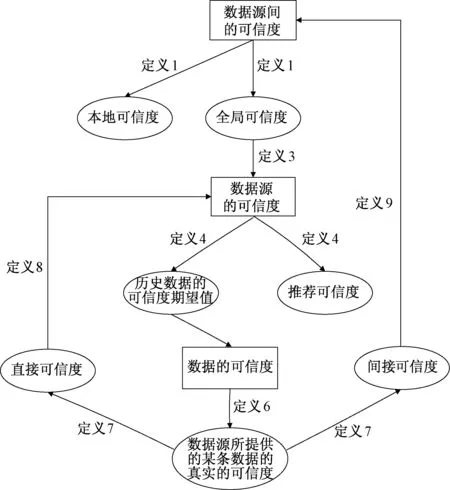
图2 数据源间、数据源及数据的可信度关联关系Fig.2 The correlation of the credibility definition of between data sources, data, data source
2 案例分析及验证
本文采用Hadoop平台搭建了一个由16台笔记本电脑组成的集群实验环境。为了验证论文所提的方法具有很好的实用性,仿真实验选取的对象是某电力公司调度通信中心实时运行的数据,其中包括3个发电厂、4个变电站的局部电网的运行数据。本实验对采集设备进行时钟同步,每一时刻采集到的数据都带有时标,这样就避免了时间延迟会造成对数据的惩罚,便于分析。
实验中静态信息仍然存储在关系数据库里。为模拟实际场景里的数据产生网络,实验中将一台PC机当作信息生成发送端。每条信息包括数据源编号,主题类型,时间,数据源可信度值,数据可信度值,风速平均,有功功率平均,无功功率平均,风向角平均,发电机转速平均值,叶轮转速平均值,叶尖压力平均值,系统压力平均值,偏航角度平均值,齿轮油温度平均值,齿轮箱轴承温度平均值,环境温度平均值,发电机前轴温度平均值,机舱温度平均值,发电机后轴温度平均值,大发电机温度平均值,A、B相电流平均值,A、B相电压平均值,频率平均值,功率因数平均值,有功功率最大值,有功功率最小值,无功功率最大值,无功功率最小值等信息,各个信息之间用逗号隔开;信息存储到以数据源编号和时间组成的文件里,如表1所示。

表1 信息及文件名格式
2.1 仿真实验设计
在智能电网环境下,数据源是指可信虚拟网络中提供数据的实体,即电力系统中提供数据的设备,记作entity;数据是指实体(数据源)关于某个主题提供的数据;主题是指数据的附属主体,记作theme。一个数据源的行为可以被认为是在一定的时间内,针对一个主题提供的数据,则存在这条数据属于数据源,记作data∈entity,这条数据附属于对应的主题,记作data∈theme,这个主题属于数据源,记作D(entity)={data|data∈entity}。一个数据源提供的所有的数据集合记作theme∈entity,一个数据源与所有有联系的主题集合记作T(entity)={theme|theme∈entity},一个主题所包含的数据集合记作D(theme)={data|data∈theme}。
本模型所涉及的参数个数比较多,其中,涉及数据源之间可信度的参数包括数据源的数量N、本地信任度权重系数α1、全局信任度权重系数β1、本地信任度直接可信度权重系数α2、本地信任度相似程度的认可度权重系数β2、本地可信度的时间衰减系数μL(t)、本地可信度的惩罚系数λL(t)、数据或行为的相似度阈值η、两次计算时间的差值Δt,涉及数据源可信度的参数包括历史数据的可信度期望值权重系数α3、推荐可信度权重系数β3、数据源可信度的时间衰减系数μS(t)、数据源可信度的惩罚系数λS(t)、以数据源为圆心的层次n、多维层次的信任权重向量γn,涉及数据可信度的参数包括直接可信度权重系数α4、间接可信度权重系数β4。
本实验把所采集的数据分成两部分,其中一部分是作为前期的电力可信虚拟网络的建立,对网络进行反复训练,同时调整更新参数的值以适应环境的变化,另一部分数据则是验证本模型的稳定性、准确性。实验参数值是基于主观性和经验性的选取的,但在后期的实验过程中是在不断的修改参数值,以便选择更合理的参数值,各参数的设置情况如下表。
2.2 算法分析过程
在Hadoop中运行过程,首先收集数据,将收集到数据进行预处理,在map过程,输入的key-value对是由采集到的数据源的标示作为key值,对于value值则是对应格式化的一行字符串,每位都有不同的含义,具体要看收集的数据源的特点,在map过程中,通过对每一行字符串的解析,主要是对value的关键位(对描述数据关键信息的位)的取舍和对key值的修改,将数据源提供数据按主题类型归属的进行分类,作为新的key值,这样就得到所需要的key-value对作为输出;在reduce过程,将map过程中的输出,按照相同的key值中将value放到同一个列表中作为reduce的输入,这时就需要使用本文模型提出的算法进行数据源间可信度、数据源可信度、数据可信度的并行计算及可信虚拟网络的构建。同时启动其他的辅助进程用来修改已经组建的可信虚拟网络,同时将程序进入下一轮的迭代计算。

表2 仿真实验中默认值参数列表
结合1.2、1.3、1.4小节内容,首先从式(1)计算数据源间的可信度开始,计算任意一个entity对其他entities的可信度,其中,需要根据式(2)和式(3)计算两方面的内容,一方面,需要对其它的entities计算本地可信度,如果数据源之间有上下文交互(条件1)或出现新的行为(条件2),那么需要更新本地可信度,如果没有新的行为,那么就按时间惩罚因子对其进行时间惩罚。其中,如果满足上述条件1任意两个数据源之间有联系,或者满足上述条件2在对数据源间本地可信度计算中,如果任意两个数据源对于同一主题提供的数据相似度超过系统设定的阈值η,那么他们之间就建立了一条有向链路,其中链路上的权值就是数据源间可信度的值。另一方面,需要对这个entity计算全局可信度。
再次,利用式(4)计算entity可信度,其中,如果entity提供的所有历史数据的可信度期望值或在整个可信虚拟网络中各层对entity的推荐可信度发生变化,那么就更新entity可信度,如果可信度没有发生变化,同样也要对其进行时间惩罚。
最后,根据式(7)利用对立事件概率来计算某个entity对一个theme提供data的可信度,其中,式(8)给出了entity对提供的data的真实的可信度,式(9)和式(10)分别给出entity对data的直接可信度和相邻entities对data的间接可信度。在实验验证中,如果某个entity提供了某种恶意的、不真实的data时,本模型会对其进行严厉惩罚,使其在可信虚拟网络中可信值瞬间变的很低,但如果在后期行为正常情况下,可信度也会随着自己信用的提升而缓慢提升,可信评估计算过程本身就是不断迭代更新的过程。整个算法的程序流程图如图3所示。
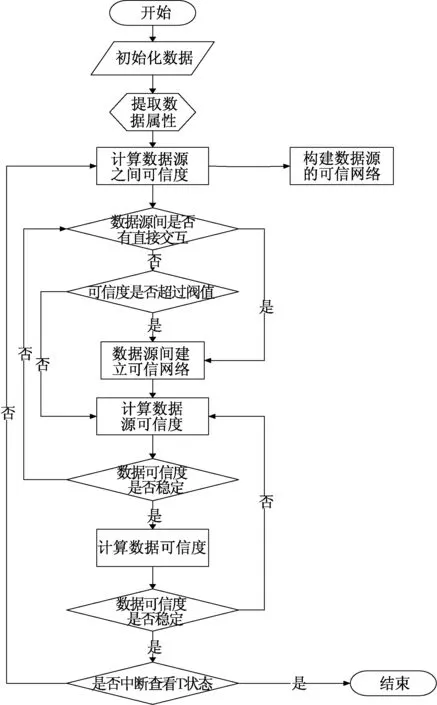
图3 电网大数据可信性度量方法的程序流程Fig.3 Program flow diagram of credibility evaluation method for Smart Grid Big Data
2.3 实验结果及分析
结合上述算法过程,将上面采集到的数据导入模型中进行验证。在实验过程中,人为拟造一个电力设备来提供的数据,主要是验证本模型对于错误数据的检测、处理能力。由于数据源之间可信度、数据源可信度、数据可信度是相互关联的,是反复嵌套迭代计算得到的,利用式(1)、式(4)、式(7)迭代的计算模拟设备的可信值,观察该拟造设备的可信度值随时间变化情况,如图4所示。

图4 人为拟造电力设备的可信值随时间变化趋势Fig.4 Artificial power equipment’s credibility value changing with time trend
从图4中可以看这一电力设备在T0-T30,电力设备的可信度呈现一种上升趋势,其中在T12-T18时间段内,电力设备的可信度呈缓慢下降趋势,这主要是由于没有新的行为,其可信度要施加时间惩罚;在T31时,通过人为修改采集的真实数据,使得这一时刻提供的数据与真实数据差距很大,由于电力设备做出了一种不可信的行为或者数据错误,本系统对其施加了惩罚,导致其可信度下降到0.1以下;在T32以后,由于电力设备的行为正常,随着时间恢复原先上升的趋势,但趋势比较缓慢。
在某一时刻,分层数据源组成的可信虚拟网络部分拓扑示意图以及多层数据源对某条数据的可信传递模拟示意图如图5所示。
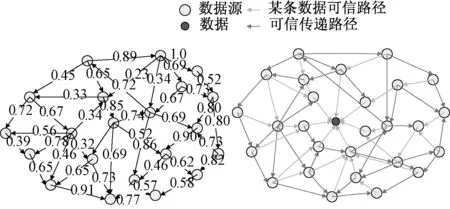
图5 某时刻可信虚拟网络部分拓扑Fig.5 The partial topological diagram of credibility network at a certain time
某个网络节点设备仅仅是整个可信虚拟网络的一部分,不能单独考虑,其单个网络节点的可信度的作用是为计算数据源之间可信度提供数据。网络节点设备的可信度是受其提供的数据可信度制约,图2描述了数据源之间的可信度、数据源的可信度、数据的可信度三者之间的依赖关系,通过反复迭代地计算三者的可信度,动态地构建大数据的可信性分析网络,然后通过所构建的稳定的可信性分析网络来计算出数据的可信度。其中,由定义2可知,利用式(2)计算智能电网中数据源间的本地可信度时,可构建数据源间可信虚拟网络,如图5(a)所示给出部分分层数据源网络拓扑图,箭头方向是指某数据源对指向数据源的联系,权重为数据源之间的可信度值,如图5(b)所示则是给出针对某条数据的可信虚拟网络示意图,从中我们可以得出,任何一条数据不仅与其提供者有直接联系,而且也有很多与之有直接或间接联系的数据源包围,形成了一个小型可信虚拟网络,这样就能大大提高对一条数据可信性评价的准确性。
在仿真实验过程中,设置数据规模为30 GB,不断的增加节点数量,本文分别设置了2、4、8、16节点数,图6反映的是对于处理同一数据量的数据,使得可信虚拟网络达到稳定时,计算的时间花费随节点个数的增加变化趋势,从实验结果可以得出其变化大致呈现一种线性趋势。

图6 模型计算时间随选取的节点个数变化趋势Fig.6 Model calculation time changing with the number of selected nodes
在实验过程中,对于数据源间的可信度度量公式考虑到本地和全局可信度;对于数据源的可信度度量公式考虑到其提供历史数据的可信度与可信虚拟网络中各层对其的推荐可信度;对于数据的可信度度量公式则考虑到其对立事件的概率。上述模型的可信度计算函数,本文都考虑到时间是影响可信度计算的重要因素之一,除此之外,数据源的行为特征也是本文考虑的重要因素,同时添加了行为特征惩罚因素。
3 结 论
本文通过分析电网数据的典型特征和属性,结合电力系统不良数据辨识模型和数据可信分析模型,给出了电网数据的可信度量的分析模型,提出了可信虚拟网络构建方法。选取电网数据实例,验证了模型可行性。实验结果表明该模型在数据源提供数据量越多的情况下,越能对所提供电网数据的可信度进行准确分析,很好地满足了电网数据的可信需求。但本文的模型有些方面需要进一步的研究,一方面,本文模型的参数值是基于主观性和经验性选取的,需要进行多次调整以适应不同的场景,另一方面,对于构建电网可信性分析网络的方法仍需要完善,这些都是今后的进一步研究工作的重点。
[1] 张东霞, 苗新, 刘丽平, 等. 智能电网大数据技术发展研究[J]. 中国电机工程学报, 2015, 35(1): 2-12.
[2] HAO Jinping, PIECHOCKI R J, KALESHI D, et al. Sparse malicious false data injection attacks and defense mechanisms in smart grids[J]. IEEE Transactions on Industrial Informatics, 2015, 11(5): 1198-1209.
[3] 高昆仑, 辛耀中, 李钊, 等. 智能电网调度控制系统安全防护技术及发展[J]. 电力系统自动化, 2015, 39(1): 48-52.
[4] 李文武, 游文霞, 王先培. 电力系统信息安全研究综述[J]. 电力系统保护与控制, 2011,39(10):140-147.
[5] DURAN-PAZ J L, PEREZ-HIDALGO F, DURAN-MARTINE M J. Bad data detection of unequal magnitudes in state estimation of power systems[J]. IEEEPower Engineering Review, 2002, 121(5): 57-60.
[6] HUANG SHYH-JIER, LIN JEU-MIN. Enhancement of anomalous data mining in power system predicting-aided state estimation[J]. IEEE Transactions on Power System, 2004, 19(1): 610-619.
[7] 孟建良, 刘德超. 一种基于Spark和聚类分析的辨识电力系统不良数据新方法[J]. 电力系统保护与控制, 2016, 44(3): 85-91.
[8] 王兴志, 严正, 沈沉, 等. 基于在线核学习的电网不良数据检测与辨识方法[J]. 电力系统保护与控制, 2012,40(1): 50-55.
[9] 张艳军, 葛延峰, 高凯, 等. 基于广域测量系统的新息图辨识不良数据方法[J]. 电力系统自动化, 2010, 34(23): 25-29.
[10] 王守信, 张莉, 李鹤松. 一种基于云模型的主观信任评价方法[J]. 软件学报, 2010, 21(6): 1341-1352.
[11] 唐文, 陈钟. 基于模糊集合理论的主观信任管理模型研究[J]. 软件学报, 2003, 14(8): 1401-1408.
[12] 李玲玲, 朱芬芬, 姚致清, 等. 基于可信度的可靠性度量云模型[J]. 电力系统保护与控制, 2012, 40(8): 90-94.
[13] 张仕斌, 许春香. 基于云模型的信任评估方法研究[J]. 计算机学报, 2013, 36(2):422-431.
[14] 张琳, 刘婧文, 王汝传, 等. 基于改进D-S证据理论的信任评估模型[J]. 通信学报, 2013, 34(7): 167-173.
[15] 赵秋月, 左万利, 田中生, 等. 一种基于改进D-S证据理论的信任关系强度评估方法研究[J]. 计算机学报, 2014, 37(4): 873-883.
[16] 张巍, 朱艳春, 孙宝文, 等. 基于模糊认知图和证据理论的FCM-DS信任模型[J]. 小型微型计算机系统, 2016, 37(6): 1259-1262.
Research on Credibility Measurement Model of Power Grid Data
CHENG Xiaorong, LI Tianqi
(1. School of Control and Computer Engineering, North China Electric Power University, Baoding 071003, China)
The untrusted data in power system reduces the accuracy of the state estimation results. The credibility requirement of data in the power grid is analyzed and identification of bad data in the grid and the theories of credible data are studied. On the basis of these studies, a hierarchical and dynamic credibility analysis model for grid data was established which takes into account weight factors such as time factor and penalty factor. Credibility analysis of power data can be summarized as combinatorial problems including data source, relations between different data sources and network path of data dissemination. The virtual network of the credibility which was on the base of dependent relationship of data source was dynamically established by calculating the credibility between data sources, the credibility of data and the credibility of data source. And the overall credibility of data is normally evaluated by the virtual network. The simulation results show that the model can satisfy the requirement of the credibility estimation of grid data, and also provide ideas to solve the problem of the credibility measurement for further research.
power grid data; big data; credibility; dynamism; trusted computing
10.3969/j.ISSN.1007-2691.2017.02.12
2016-07-19.
TM711
A
1007-2691(2017)02-0083-08
程晓荣(1963-),女,教授,主要研究方向为计算机网络应用、网络信息安全;李天琦(1989-),男,硕士研究生,主要研究方向为计算机网络应用、网络信息安全。
