考虑机组重要度和负荷停电损失的网架重构分层协调优化

刘文轩，顾雪平，李少岩

(华北电力大学 电气与电子工程学院，河北 保定 071003)

考虑机组重要度和负荷停电损失的网架重构分层协调优化

刘文轩，顾雪平，李少岩

(华北电力大学 电气与电子工程学院，河北 保定 071003)

电力系统大停电后，重要负荷的损失状况会随时间的推移而逐步增大，成为系统恢复的重点关注问题。研究了网架重构阶段机组与重要负荷协调恢复的优化方法，以热启动机组的总容量和恢复过程中的总负荷损失分别作为上、下层目标函数，建立了双层优化模型；引入灰关联模型对机组综合重要度进行评估，采用基于状态优选的多层编码遗传算法进行求解，获得各机组热启动总容量；结合网络计划技术，对各节点重要负荷的恢复时间进行计算，评估不同方案的负荷损失情况，获取机组与重要负荷协调恢复的最优方案。新英格兰10机39节点系统的算例结果验证了本文方法的有效性。

网架重构；负荷损失；机组重要度评估；状态优选；网络计划技术

0 引 言

现代互联电网规模日益增大、电压等级越来越高，提升系统运行经济性和可靠性的同时，也对电网安全稳定运行提出了严峻的挑战。随着区域系统之间电气联系的日益加强，局部系统的故障可能会由于调度处理不当、保护和自动装置的不正确或不协调动作酿成大面积的停电事故，甚至导致整个电力系统崩溃瓦解，带来巨大的经济损失和社会混乱[1-4]。因此，研究大停电后的恢复控制，对于优化系统恢复措施、实现快速有序的恢复、减小停电损失具有重要意义。

目前国内外的研究人员对大停电后的恢复工作进行了深入研究，取得了丰富的研究成果。文献[5]提出了一种考虑节点恢复可靠性的网架重构优化方法， 但是并未涉及机组接力式启动与负荷恢复的先后顺序。文献[6]考虑负荷类型及停电损失的负荷恢复策略优化，但是并未涉及机组、网架与负荷的协调恢复。文献[7]分析了机组启动过程中负荷恢复的特点，提出了与机组启动过程相协调的负荷恢复方式,但是并未提及机组与负荷的恢复时间，难以评估全网损失。文献[8]提出了一种网架拓扑分析方法，但是最优方案的选取过程并未考虑负荷量及其造成损失的影响。文献[9]研究机组启动与负荷恢复的交叉影响，提出一种针对网架重构阶段负荷恢复的优化方法，但是采用固定时段划分方式恢复重要负荷，可能增大部分负荷的等待时间。

电力系统恢复问题是一个复杂的多目标、非线性的组合优化问题，难以建立较为全面的优化模型。以往建立的模型通常采用 “分时段建模”方式进行求解[10-11]，由于系统内设备特性各异，难以确定有效的时段划分方式，导致求解误差较大。

针对上述问题，本文以热启动机组的总容量和恢复过程中的总负荷损失分别作为上、下层目标函数，提出了一种双层优化模型。引入灰关联模型对机组综合重要度进行评估，采用基于状态优选的多层编码遗传算法进行求解，获得各机组热启动总容量。根据网络计划技术，对各节点重要负荷的恢复时间进行计算，将时段设置的影响降至最低，根据机组与节点的恢复时间，确保更加精确地评估负荷损失，获取机组与重要负荷协调恢复的最优方案。

1 网架重构的双层优化模型

1.1 目标函数

网架重构前期主要以启动机组为核心任务，以确保为后续恢复提供充足的功率支持。然而在机组恢复过程中，也需要恢复一定量的负荷，主要有两方面考虑：系统运行方面，火电机组需要带一定量的负荷保证其稳定运行，称为最小稳定出力[7,12-13]，一般为机组额定容量的20%～30%；经济性方面，部分负荷的长时间停运会造成较大的经济损失，甚至导致民众生命安全受到威胁，需要尽快恢复。由此可见，电力系统可恢复的负荷量与已恢复的系统规模正相关，也从客观上反映了系统的恢复程度。

机组恢复与负荷恢复是一个同时交替进行的过程，需要统筹兼顾。本文以热启动机组的总容量作为上层目标函数，恢复过程中的负荷损失作为下层目标函数，建立双层优化模型进行求解。

(1)热启动机组总容量

大停电发生后，从快速恢复负荷以减小停电损失的角度出发，最优恢复方案应该使热启动机组的总容量最大，以确保后续恢复工作得到充足的功率支持。恢复方案中机组的容量成为关键优选指标，在制定恢复方案时，将可热启动恢复机组的额定出力之和作为上层优化目标，如式(1)所示。

(1)

式中：N为整个恢复过程总的时段数；NA为系统中待恢复机组的总台数；cik表示机组i是否在第k时段投入，投入为1，否则为0；PMi为机组i的额定容量。

(2)负荷损失

电力系统通常根据用户在国民经济中的重要地位将其划分为Ⅰ类负荷、Ⅱ类负荷和Ⅲ类负荷，同时也代表了大停电后负荷紧急恢复的迫切程度与损失状况。对于许多重要负荷，损失状况会随停电时间的推移而逐步增大。大停电发生后，确保负荷损失最小是选择最优恢复方案的重要标准。本文针对各厂站待恢复负荷的类型差异和停电损失的不同，以恢复过程中的负荷损失费用最小为下层优化目标，合理安排机组与负荷协调恢复计划，如式(2)所示。

(2)

式中：Li(t)为节点i上的负荷在t时刻的费用损失函数；Pi(t)为t时刻节点i上未恢复的负荷量；Nk为恢复方案中负荷节点数；T为恢复优化时间(本文T取所有Ⅰ类负荷恢复完成的时间)。

1.2 约束条件

(1)潮流约束

①等式约束

含有Nb个节点的电力系统，等式约束主要是潮流方程约束。

(3)

式中：j∈i表示∑号后的标号j的节点必须直接和节点i相连，包括j=i的情况；Pi为节点i有功注入；Qi为节点i无功注入；Ui为节点i电压模值；θij为节点i和节点j的电压相角差。

②不等式约束

(4)

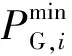
(2)机组热启动时限

为使恢复方案中火电机组快速启动并提供功率支持，应重点考虑机组的热启动时限问题[14]。机组热启动时间约束为

(5)

式中：TS,i为机组恢复厂用电时间；TCH,i为机组i的热启动时限。

将问题的目标函数和约束条件融合在一起，构建双层优化模型，其结构如图1所示。

图1 双层优化模型结构图Fig.1 The structure of bi-level optimization model

图1中，约束条件通过变形统一为等式约束Gj(X)和不等式约束gj(X)；设计变量X=[X1,X2,X3,X4,X5]，具体如下：

①X1=[C1,C2,… ,CN]

其中，Ci={ci1,ci2,…,ciNA}(i=1,2,…,N)

②X2={P1(t),P2(t),…,PNk(t)}

③X3={P,Q,U,θ}

④X4={PG,QG,U,PL}

⑤X5={TS,1,TS,2,…,TS,NA}

2 机组综合重要度评估

2.1 影响机组重要度因素

系统恢复过程中，机组的恢复是核心内容，本节综合考虑机组与重要负荷距离、机组的热启动时限、额定容量、启动时间、机组爬坡时间和机组启动功率6个方面因素(如表1所示)，对机组重要度进行评估，以确定机组启动的优先顺序。

表1 机组重要度评价指标

表1中部分指标定义如下:

(1)机组与重要负荷距离

电网恢复的首要目标是尽快为重要负荷供电，以减小停电损失。在大停电初期，系统相对脆弱，为避免长距离送电，缓解充电无功过剩带来的线路末端电压升高问题；同时减少设备操作次数，提高送电可靠性，应优先恢复距离重要负荷较近的机组。机组与重要负荷的距离定义为

(6)

式中：NT表示具有重要负荷的节点数；Pj表示节点j(j=1,2，…，NT)的Ⅰ类负荷量；Bij表示机组i与节点j之间最短路径的充电电容。

(2)机组启动时间、爬坡时间与额定出力

采用图2所示机组出力简化曲线描述各机组的启动爬坡过程。将机组i的恢复过程分为三个阶段：等待恢复时间(0～TSi)，机组启动时间(TSi～TKi)，机组并网后出力爬坡时间(TKi～TRi)。其中，T(i,1)为机组启动时间(指标Ii4)，T(i,2)为机组爬坡时间(指标Ii5)。

图2 机组出力简化曲线Fig.2 Simplified curve of unit output

2.2 基于灰关联模型的机组综合重要度评估

灰色关联法[15-16]是综合灰色系统理论和逼近思想的多属性决策方法，可以很好地解决实际系统中的多属性决策问题，且有较高的决策灵敏度。根据2.1节所述，本文首先采用文献[17]提出的模糊反熵权法反映决策者主观偏好和客观权重，求得各指标的权重为

(7)

再通过灰关联模型综合考虑各项指标，评估机组重要度。具体评估过程如下：

(1)决策矩阵规范化

构造有n个机组m个指标的决策矩阵Β=(bij)n×m,i∈[1,n],j∈[1,m]，经过规范化处理得规范化矩阵R=(rij)n×m。规范化方法如下：

效益型指标

(8)

成本型指标

(9)

(2)设

(10)

(11)

则正理想指标集与负理想指标集如式(12)和式(13)所示。

(12)

(13)

(3)计算机组i与正负理想指标集关于指标j的灰关联系数分别为

(14)

(15)

其中，ρ为分辨系数，ρ∈[0,1],一般取ρ=0.5。

(4)计算机组i与正负理想指标集关于指标j的灰关联度分别为

(16)

(17)

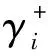
(5)定义优属度ui来综合衡量机组i靠近正理想指标集和远离负理想指标集的程度。机组i以优属度ui趋近于正理想指标集，同时以1-ui趋近于负理想指标集。根据最小平方和准则，建立目标函数：

(18)

(19)

把优属度ui作为参评机组重要度的综合指标，对其进行降序排序，ui值越大的机组重要度越高。

3 基于多层编码遗传算法的恢复方案优化

3.1 多层编码遗传算法

在每一时段的恢复过程中，由目标函数和约束条件组成的背包问题，被证明是一个NP完全问题。由于网架重构采用分时段策略，其中的单一时段优化相对简单，采用传统遗传算法的单个染色体就可以表示此时段的解[10,15]；而全过程最优解相对复杂，需要多个染色体联合表示。因此，本文引入多层编码遗传算法(Multi-Layer Coded Genetic Algorithm，MLCGA)[18]对网架重构全过程优化进行求解，算法结构如图3所示。

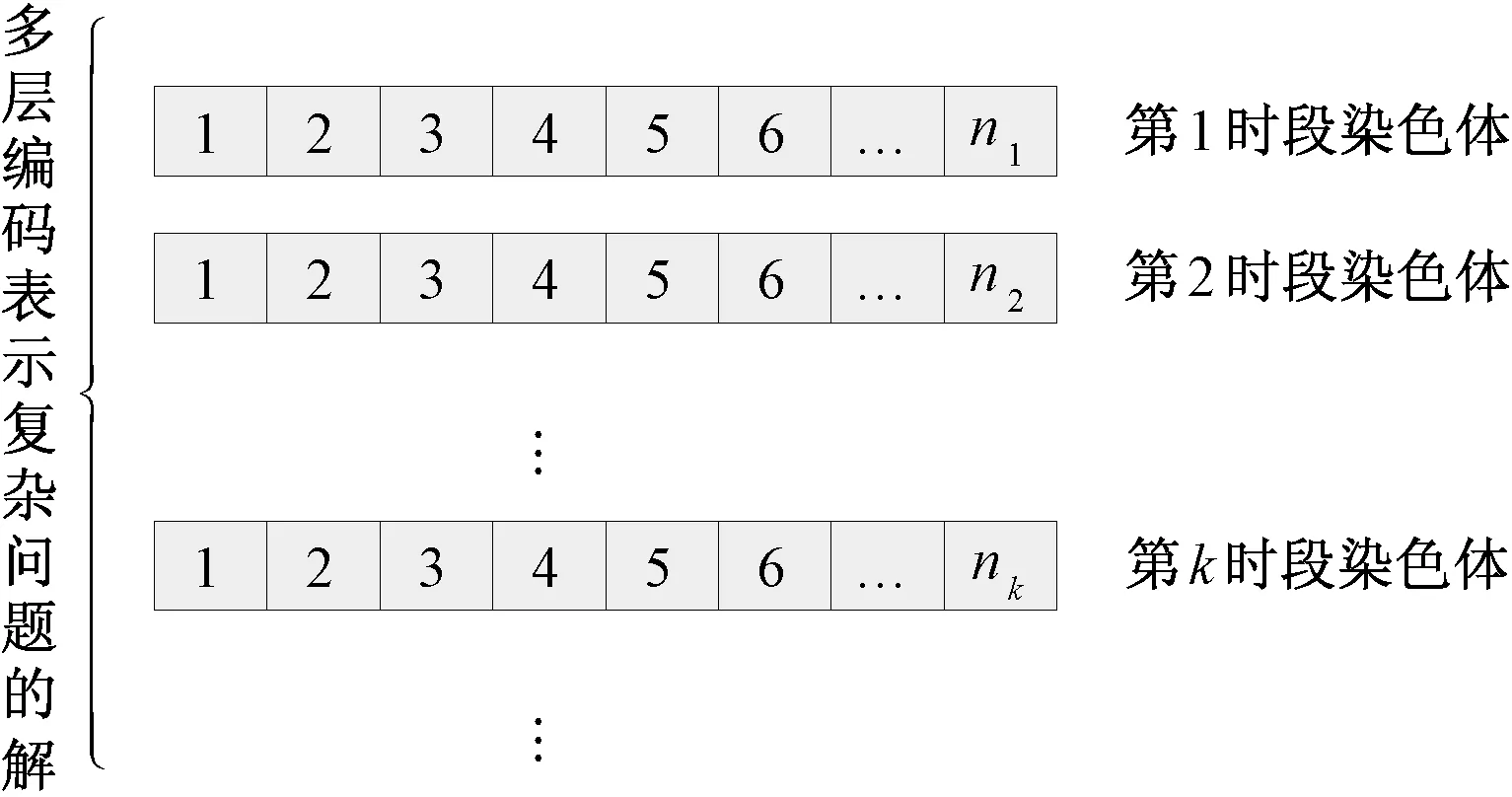
图3 多层编码遗传算法示意图Fig.3 Structure of the MLCGA

由此可以看出，时段数决定了遗传算法编码层数；每一时段染色体长度由待恢复机组数决定，每一位基因代表一个机组的恢复状态，基因编码采用二进制，1代表恢复，0代表不恢复；多个时段的解共同组成了全恢复过程的解。

以往的分时段决策思路在每一时段仅保留一个方案，将每个时段方案的串行组合作为全过程最优方案，求得的方案只是局部最优方案，与实际全局最优解偏差较大。本文采用一种状态优选方法，在每一时段完成机组选择后，保留此时段方案中指标最高的前Rk个状态，确保接近全过程最优[19-20]。同时，在迭代过程中，为减小程序运行时间，对终止判据进行修改：采用最优个体最小保持代数Maxgen作为终止依据，若已搜索到的最优个体适应度值在Maxgen代内保持不变，则认为此个体为最优个体，终止迭代。

3.2 基于网络计划技术的恢复方案优化

网络计划技术是20世纪50年代源于美国的一项计划管理技术，旨在对项目进行科学地组织、指挥、协调和控制，以达到缩短工期、提高效率、节省劳力、降低成本消耗的目标[21-22]。目前传统黑启动机组优选与路径搜索算法的研究已较为成熟，对于负荷恢复也涉及较多。然而对网架重构与负荷恢复过程中的相互影响考虑不足，并且大多数文献对于并行恢复时间的评估并不明确，部分仍然延用串行恢复的计算方法，导致总恢复时间计算出现偏差。本文结合网络计划技术中的关键线路概念，根据各时段并行恢复特点制定相应的恢复策略，将机组、线路和负荷恢复过程协调考虑，建立组合恢复的协调优化模型，在多个目标节点并行恢复中最大限度利用系统功率，实现系统网架的快速重构。

电力系统大停电后的恢复工作是一个技术高度密集的综合性系统工程。通常情况下，影响恢复进程的主要因素是可用功率不足，优化问题属于“功率有限—时间最短”。根据各工序对网络计划工期的影响程度，将有限的功率进行逐时段科学合理地分配，确保负荷损失最小。功率优化配置的原则如下。

(1)关键线路优先恢复。本文将恢复机组节点的路径作为关键线路，按照机组综合重要度确定功率分配的优先顺序。若超出系统可提供的总功率，则延迟恢复综合重要度小的机组。

(2)非关键线路在满足关键线路以后再进行恢复。当遇到功率不足时，按照遗传算法基因编码随机延迟其中的部分节点恢复，并根据时段的损失情况评估恢复效果，进行遗传算法的选择、交叉和变异。

主要步骤如下。

(1)实时统计系统电源有功P和进相运行能力Q，作为系统功率上限。

(2)将某一时段中的各工作按顺序编号，从第1号到第n号。按编号由小到大顺序，统计其消耗的功率，并依次分配P和Q。

(4)经过时间Δt后，重新进行(1)～(3)的步骤，直到所有恢复工作有功和无功之和均不大于P和Q。

3.3 恢复方案优化的算法实现

在遗传编码中，每个染色体表示一种恢复方案，根据各染色体计算目标函数值。在为拟启动机组搜索供电路径时，为降低线路末端工频过电压，应优先选择充电无功较小的线路，本文将线路充电无功作为线路权值，结合Dijkstra算法进行路径搜索，构建恢复网架。主要计算流程如附录A图A1所示。

由于火电机组有最小稳定出力要求，因此在进行潮流校验时，默认新并网的机组功率为其最小稳定出力。同时接入路径上的Ⅰ类负荷，若仍然无法满足最小出力，再接入相应量的Ⅱ类负荷和Ⅲ类负荷。参照文献[23]，此类负荷一般在电压较高节点接入。

在获取最优方案集之后，对基因编码表达形式做了重新设计，如图4所示。每位基因由两位数字组成，第一位为时段编号，第二位为此时段机组启动次序，只对第二位基因进行选择、交叉和变异。采用网络计划技术思想，结合多层编码遗传算法评估各方案时间，具体流程详见附录B。

图4 基因编码形式表达示意图Fig.4 Structure of coding form

4 算例分析

4.1 算例原始数据

本文首先以新英格兰10机39节点系统为算例验证所提方法的有效性，该系统的结构如图5所示。设节点30为黑启动电源，装机容量为2×250 MW，额定功率因数为cosφ=0.9，机组空载时所吸收的最大无功功率为0.3SN。系统主要机组参数如表2所示，其中Pcr为机组厂用电所需功率，各机组最小稳定出力为额定出力的25%；各线路、变压器的恢复时间详见附录C；主要节点重要负荷比重如表3所示。

图5 新英格兰10机39节点系统Fig.5 New England 10-unit 39-bus power system

利用第3节所述算法对恢复方案进行优化求解，多层编码遗传算法主要参数设置如下：每层种群包含40条染色体，交叉概率为0.8，变异概率为0.1， 最优个体最少保持代数Maxgen设为10。

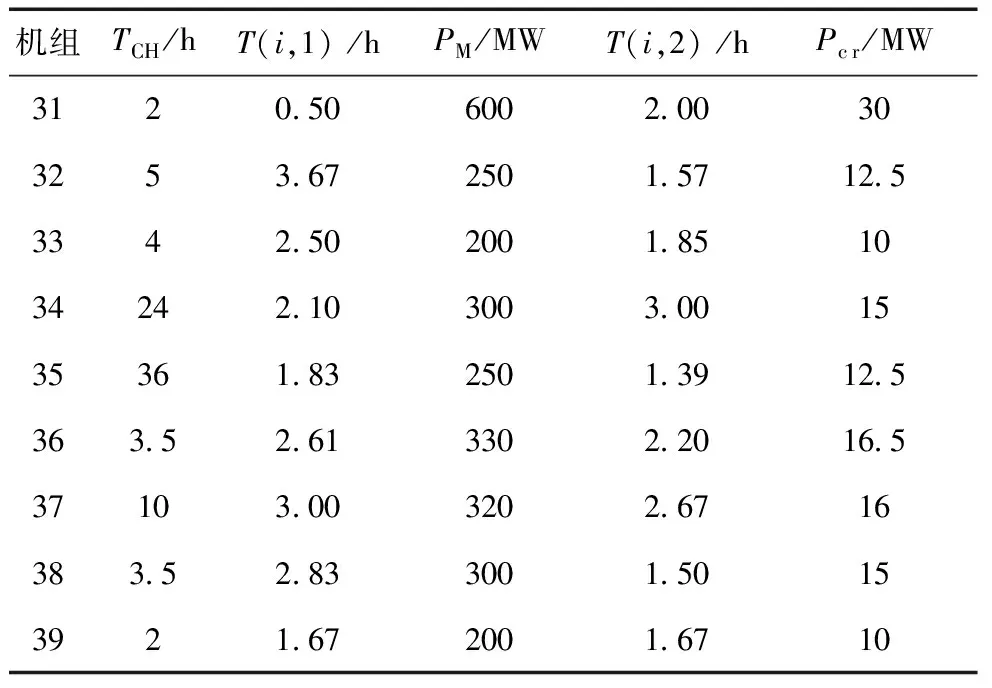
表2 新英格兰10机39节点系统机组参数

表3 主要节点负荷比重

表4列举了各类负荷的平均停电损失费用情况，可以看出，随着停电时间的延长，经济损失也会增大。利用最小二乘法作出负荷损失时变曲线(三次函数拟合)，如图6所示。

表4 用户停电损失

根据此情况重点恢复Ⅰ类负荷，兼顾部分Ⅱ类负荷，可将大停电后的社会影响和经济损失降到最低。

图6 负荷平均损失时变曲线Fig.6 The curve of average loss for load

4.2 算例结果

根据2.2节所述模型，对机组综合重要度进行评估，由3位专家根据自身经验赋予三个目标函数主观权重，如表5所示。

表5 专家赋予的主观权重

采用灰关联模型进行机组重要度评估，所得结果如表6所示。可知机组重要度排序为：39≻31≻33≻38≻32≻36≻35≻34≻37(“A≻B”表示机组A的综合重要度高于机组B)。

表6 待启动机组综合重要度

根据第3节所述的算法进行求解，得出最优方案与一组对比方案，如表7所示。其中，虽然节点38 和节点39的机组重要度较高，但是由于所处节点距离黑启动电源较远，且热启动时限较短，为确保总体恢复效果的最优，只能进行冷启动恢复。

最优方案的恢复路径如图5彩色线段所示，恢复所有Ⅰ类负荷共用时3.31 h，作为下层目标函数的优化时间。

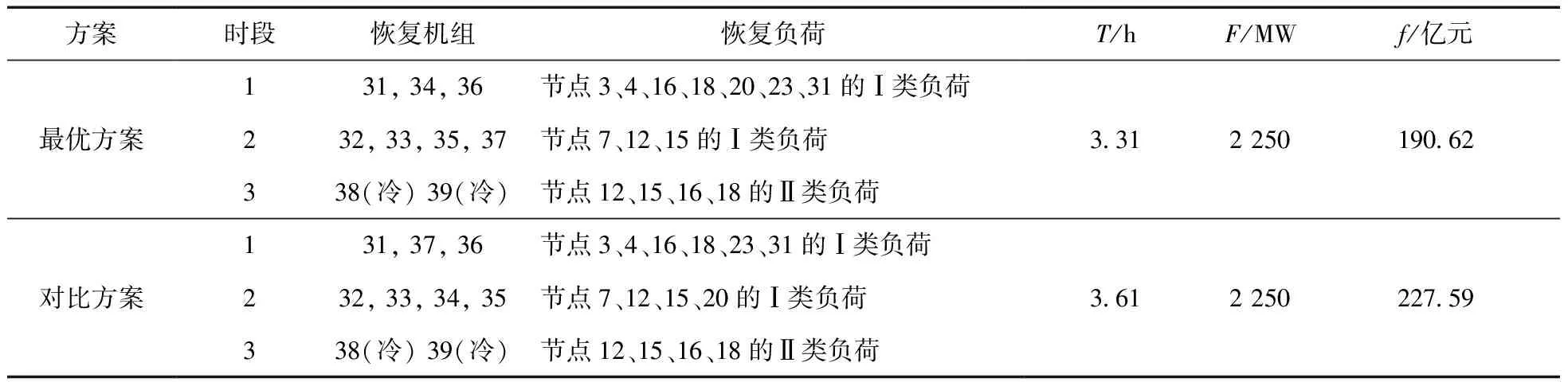
表7 新英格兰10机39节点系统备选恢复方案

应用网络计划图表示最优方案恢复过程，如图7所示。

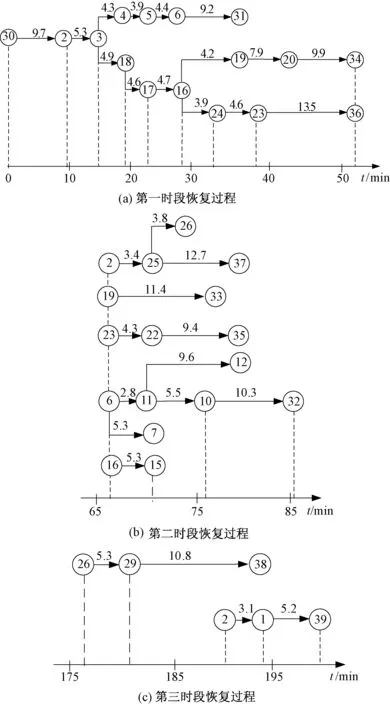
图7 最优恢复方案网络计划图Fig.7 The figure of network planning for optimal scheme

4.3 结果分析

从上述算例可以看出，采用本文所提方法明确各时段工序的衔接关系，与文献[9-11]采用的严格分时段优化方法相比，可以在一定程度上减少时段划分造成的等待时间，各节点的恢复时间不再受时段的限制，确保负荷损失评估更加准确。

最优方案和对比方案的上层目标函数值相同，均能确保热启动机组的总容量为2 250 MW；而下层目标函数则有差异，主要是恢复过程中机组启动的先后顺序导致网架差异，进而影响负荷恢复时间。最优方案在3.31 h内恢复所有Ⅰ类负荷与部分Ⅱ类负荷，形成了4台机组并列运行的小系统(总容量1 650 MW)，共恢复Ⅰ类负荷442.50 MW，Ⅱ类负荷173.91 MW；而恢复同样的负荷，对比方案则需要3.61 h完成恢复任务，延迟了恢复时间，增加了负荷损失。主要是由于最优方案在第一时段内优先恢复34节点机组，构建的网架包含更多重要负荷节点。可见，机组恢复过程中网架的构建对减小负荷损失具有重要作用。在不影响机组热启动总容量的基础上，适当改变机组和相应网架的恢复顺序，确保重要负荷优先恢复，可以有效降低国民经济损失，缓解大停电造成的不良社会影响。

5 结 论

本文提出一种考虑负荷损失的网架重构恢复方案优化方法。针对大停电后负荷损失随变化的问题，以热启动机组的总容量和恢复过程中的总负荷损失分别作为上、下层目标函数，建立了双层优化模型；引入灰关联模型对机组综合重要度进行评估，采用基于状态优选的多层编码遗传算法进行求解，获得各机组热启动总容量；根据网络计划技术，对各节点重要负荷的恢复时间进行计算，评估不同方案的负荷损失情况，获取机组与重要负荷协调恢复的最优方案。新英格兰10机39节点系统的算例结果验证了本文方法的有效性。本文提出的方法可以比较准确地计算机组与重要负荷的恢复时间，可更加客观地反映大停电后的系统损失情况。避免了分时段决策造成的过多等待时间，确保各工序有条不紊进行，对系统恢复方案的制订具有较强的参考价值。

[1] ADIBI M M, KAFKA R J. Power system restoration issues[J]. Computer Applications in Power, IEEE, 1991, 4(2):19-24.

[2] 张硕, 张沿辉. 基于混合回归黑启动操作过电压的快速预测[J]. 电力科学与工程, 2009, 25(5):11-15.

[3] QIN Z, HOU Y, LIU C C, et al. Coordinating generation and load pickup during load restoration with discrete load increments and reserve constraints [J]. IET Generation Transmission & Distribution, 2015, 9(15):2437-2446.

[4] FINK L H, LIOU K L, LIU C C. From generic restoration actions to specific restoration strategies [J]. IEEE Transactions on Power Systems, 1995, 10(2):745-752.

[5] 梁海平, 顾雪平. 基于节点恢复可靠性的骨架网络重构[J]. 华北电力大学学报(自然科学版), 2014, 41(4):30-34.

[6] 李亚男, 顾雪平, 钟慧荣. 考虑负荷类型及停电损失的负荷恢复策略优化[J]. 华北电力大学学报(自然科学版), 2012, 39(3):6-12.

[7] 刘映尚, 吴文传, 冯永青,等. 黑启动过程中的负荷恢复[J]. 电网技术, 2007, 31(13):17-22.

[8] 董金哲, 李少岩, 梁海平,等. 用于黑启动方案生成的对象化电网拓扑分析方法[J]. 华北电力大学学报(自然科学版), 2015, 42(2):23-29.

[9] 钟慧荣, 顾雪平, 朱玲欣. 黑启动恢复中网架重构阶段的负荷恢复优化[J]. 电力系统保护与控制, 2011, 39(17):26-32.

[10] 朱冬雪, 顾雪平, 钟慧荣. 电力系统大停电后机组恢复的多目标优化方法[J]. 电网技术, 2013, 37(3):814-820.

[11] GU X, ZHONG H. Optimisation of network reconfiguration based on a two-layer unit-restarting framework for power system restoration [J]. IET Generation Transmission & Distribution, 2012, 6(7): 693-700.

[12] 李丰. 考虑大规模风电接入系统的发电优化调度模型及方法研究[D]. 北京: 华北电力大学, 2014.

[13] 瞿寒冰. 大停电后的负荷恢复研究[D]. 济南: 山东大学, 2012.

[14] 刘强, 石立宝, 周明, 等. 电力系统恢复中机组恢复的优化选择方法[J]. 电工技术学报, 2009, 24(3): 164-170.

[15] 顾雪平, 赵宝斌, 刘文轩. 结合多目标优化与灰色关联决策的负荷恢复方法[J]. 电力自动化设备, 2015, 35(9):6-13.

[16] 李少岩, 顾雪平, 梁海平. 给定恢复目标的扩展黑启动方案路径优选[J]. 电力系统自动化, 2015，39(16): 59-64.

[17] 刘文轩, 顾雪平, 王佳裕, 等. 考虑系统安全因素的负荷恢复方案优化[J]. 电力系统自动化, 2016, 40(12):87-93.

[18] 乐美龙, 包节, 范志强. 龙门吊与集卡协同调度问题研究[J]. 计算机工程与应用, 2012, 48(14): 241-248.

[19] 张璨, 林振智, 文福拴,等. 电力系统网络重构的多目标双层优化策略[J]. 电力系统自动化, 2014, 38(7):29-38.

[20] 黎嘉明, 李大虎, 孙建波, 等. 结合状态削减技术的电力系统黑启动动态规划算法[J]. 中国电机工程学报, 2014, 34(25): 4409-4419.

[21] MOTA A A, MOTA L T M, MORELATO A. Visualization of power system restoration plans using CPM/PERT graphs [J]. IEEE Transactions on Power Systems, 2007, 22(3): 1322-1329.

[22] 李万庆，孟文清．工程网络计划技术[M]. 北京：科学出版社,2009.

[23] 刘艳, 张凡, 顾雪平. 大停电后的机组投运风险评估[J]. 中国电机工程学报, 2013,33(31):106-113.

Hierarchical Coordinative Optimization for Network Reconfiguration Considering Unit Importance and the Load Outage Loss

LIU Wenxuan, GU Xueping, LI Shaoyan

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

The outage loss of important loads may increase as time passes after a major blackout in power system, which has an adverse effect on system restoration. In this context, coordinative restoration optimization of units and load in the process of network reconfiguration is analyzed in this paper. A bi-level optimization model is established, taking the total capacity of the hot-started units and the total outage loss of loads in the restoration process as the upper-level and the lower-level objective functions respectively. The grey correlation model is used to evaluate the importance of units, and multi-layer coded genetic algorithm based on state optimization is applied to obtain the total capacity of the hot-started units. By applying network planning technology, the restoration time of important load in every node is calculated, and the loss evaluation of different schemes is carried out. Then the optimized scheme of coordinative restoration of unit and important load is obtained. The effectiveness of the proposed method is verified by the optimization results on New England 10-unit 39-node power system.

network reconfiguration; load loss; evaluation of unit importance; state optimization; network planning technology

10.3969/j.ISSN.1007-2691.2017.02.04

2016-08-08.

国家自然科学基金资助项目(51277076).

TM761

A

1007-2691(2017)02-0022-11

刘文轩( 1986-)，男，博士研究生，研究方向为电力系统安全防御与恢复控制；顾雪平( 1964-)，男，教授，博士生导师，研究方向为电力系统安全防御和系统恢复、电力系统安全稳定评估与控制、智能技术在电力系统中的应用；李少岩( 1989-)，男，博士研究生，研究方向为电力系统安全防御与恢复控制。