考虑光伏发电相关性的概率潮流计算

赵来鑫，赵书强，胡永强

(华北电力大学 新能源电力系统国家重点实验室, 河北 保定 071003)

考虑光伏发电相关性的概率潮流计算

赵来鑫，赵书强，胡永强

(华北电力大学 新能源电力系统国家重点实验室, 河北 保定 071003)

地理位置较近的光伏发电系统，输出功率之间具有相关性，会对概率潮流计算的准确性产生影响。采用改进的Nataf变换处理光伏出力之间的相关性，并结合半不变量和C型Gram-Charlier级数进行概率潮流计算。该方法不仅较蒙特卡洛法有更高的计算效率，而且能够体现变量空间之间的变换过程，对于不服从正态分布的光伏出力之间的相关性具有较好的处理效果，同时C型Gram-Charlier级数可以防止概率密度值出现负值的情况。通过IEEE14节点算例和南方某地区实际电网算例验证了所提方法的准确性和有效性。

光伏发电；相关性；概率潮流；改进的Nataf变换；C型Gram-Charlier级数

0 引 言

近年来，光伏发电系统在电网中的装机容量逐渐增大，给电网的安全稳定运行带来了许多不确定的因素[1]。光伏属于典型的间歇式能源，具有随机性，传统的确定性潮流无法准确地反映电力系统的运行状况。概率潮流(Probabilistic Load Flow，PLF)可以解决电力系统存在的各种随机性问题，因而得到了广泛的应用。PLF的概念最早是在20世纪70年代由Borkowska提出的[2]，经过40多年的完善与发展，常用的处理方法总体上分为三类：蒙特卡罗模拟方法(Monte Carlo Simulation Method，MCSM)[3,4]，点估计方法(Point Estimate Method，PEM)[5,6]，半不变量方法(Cumulant Method，CM)[7-9]。MCSM进行随机潮流计算所得的结果最为精确，而且程序结构简单易于实现，然而大量的仿真计算耗时多，因此它主要作为评估其他方法优劣的标准。PEM是PLF的近似解法，计算速度快，但计算高阶矩时误差较大。CM是解析法中比较常用的一种方法，它根据输入随机变量的概率分布特性计算各阶矩得到半不变量，再利用Gram-Charlier等级数展开得到节点电压和支路潮流的概率分布特性，它可以将复杂的卷积运算转化为半不变量之间的代数运算，减小了计算量，从而提高了计算效率，得到了广泛的应用。

传统的PLF计算都是基于输入变量之间相互独立的假设，而在实际情况中位置相近的新能源电站处于相似的气象条件下其输出功率之间具有一定的相关性，忽略这种相关性会给PLF的计算结果带来较大的误差，因而考虑新能源发电输出功率之间相关性的研究得到了越来越多的关注[10,11]。考虑相关性的PLF常用的建模方法主要有正交变换，多项式正态变换，Ronsenblatt变换，Nataf变换[12，13]。正交变换只能处理输入随机变量服从正态分布的PLF，多项式正态变换不易得到输出变量的概率分布特性曲线，Rosenblatt变换需要知道随机变量的联合概率分布信息且变换也不唯一。Nataf变换只需要知道随机变量的边缘概率密度分布和协方差矩阵，再根据需要确定联合概率密度分布的部分相关系数，然后通过恰当的等价变换，将不服从正态分布相关的多维随机变量空间变换到正态分布的独立的变量空间，在实际中较易实现。文献[13]提出了一种基于Nataf变换处理光伏出力相关性的PEM，能够处理多维随机变量之间相关性的问题，用时虽比MCSM少，但与CM相比耗时还是相当可观的。文献[14]采用半不变量的方法处理大规模风电并网的随机潮流，但由于风电随机波动较大，采用A型Gram-Charlier级数可能会出现状态量的概率密度函数值为负的情况，方法失效。

学者们对风力发电相关性PLF的研究成果较多，但关于光伏发电相关性的研究却非常少。因此，本文提出一种将线性化Nataf变换和半不变量法相结合处理光伏发电相关性的概率潮流方法。该方法不仅计算效率较高，而且能够体现相关系数在不同空间的转换，对于不服从正态分布的光伏出力之间的相关性具有优良的效果，同时光伏发电系统会使得系统注入量的随机性增强，状态量的概率密度函数值可能出现负值，因而引入采用指数形式的C型Gram-Charlier级数，避免了状态量概率密度函数值可能为负的情况。对IEEE14节点系统和南方某地区实际电网的测试结果表明本文所提的方法是有效的。

1 改进的Nataf变换

地理位置较近的光伏发电系统输出功率之间具有较强的关联特性，因此进行PLF计算时需要考虑这种相关性，否则会带来较大的计算误差，甚至会得到错误的结论。Nataf变换的条件在工程中较易实现，但它是一种非线性的变换，需要采用数值方法求解。

1.1 传统Nataf变换

文献[12]提出了如下等概率边缘变换：

(1)

式中：Φ-1(·)为标准正态分布的逆累积分布函数。

根据Nataf变换的相关理论，可以得到n维随机向量X(x1,x2,…,xn)的联合概率密度函数：

(2)

(3)

根据相关系数的定义以及(2)式(3)式，推导得到随机向量X(x1,x2,…,xn)的相关系数ρij和CY的元素ρij′之间的对应关系：

(4)

式中:μxi，μxj分别为随机变量xi，xj的均值;φ2(yi,yj,ρij′)表示标准正态随机变量yi和yj满足相关系数ρij′的联合概率密度函数。

Nataf正变换以及Jacobian矩阵可以表示为如下形式[12]：

(5)

(6)

式中：L0为相关系数矩阵CY经过Cholesky分解CY=L0L0T得到的下三角矩阵。

1.2 改进的Nataf变换

Nataf变换是非线性变换，如果将其线性化能使运算得到简化，从而使PLF的计算量减小。在Nataf变换中，首先进行的等概率边缘变换是非线性的，这会给计算带来一定的麻烦，因此可以根据“正态尾部近似原理”，采用Rackwitz-Fiessler变换[15]将式(5)中非线性的等概率边缘变换部分用等效的线性化正态随机向量进行简化，得到线性化后的Nataf变换公式为

(7)

线性化Nataf变换的逆变换形式为

(8)

传统的Nataf变换通常采用数值方法实现，而线性化的Nataf变换不仅考虑了相关系数在变换过程中的改变，而且其逆变换形式比传统的Nataf变换更简单，也更实用。当考虑光伏发电之间相关性进行潮流计算时，需要运用线性化的Nataf逆变换形式来处理这种相关性，因此计算过程更加方便。

2 考虑光伏发电相关性的PLF算法

2.1 输入变量的概率特性

在PLF的计算中，输入变量主要有常规发电机出力，负荷和光伏出力。对于常规发电机出力，假设其出力服从二项分布。对于负荷，假设其服从正态分布并且具有恒定的功率因数。

有研究表明，光伏发电与光照强度具有一定的线性关系，且光照强度和光伏输出功率在一段时间内(1 h或几个h)概率分布均服从Beta分布[16]。则光伏输出功率的概率密度函数为

(9)

式中：α和β为Beta分布的两个形状参数；Γ(·)为Gamma函数；P和PM分别为光伏发电输出的有功功率和有功功率的最大值。

2.2 线性化的潮流方程模型

考虑到节点注入功率的随机变化，将极坐标形式的系统潮流方程在基准运行点处应用泰勒级数展开，并且仅保留展开式中的一次项，可得

(10)

2.3 相关输入变量的半不变量计算

常规发电机出力和负荷分别服从二项分布和正态分布，通过常规的数值解法可快速准确地求得其半不变量[7]。对于具有相关性的光伏出力的半不变量，不能简单地通过数值解法求得，需要首先根据MCSM抽样技术生成相互独立的服从标准正态分布的样本，然后再利用线性化Nataf逆变换等技术以及相关系数矩阵得到光伏出力变量的样本，以此为基础，根据原点矩与半不变量的关系获得该变量的半不变量。

求得了节点注入功率变化量ΔW的各阶半不变量，再根据(11)式就可以得到各个节点状态变化量ΔX以及各条支路功率变化量ΔZ的各阶半不变量：

(11)

2.4 应用改进Gram-Charlier级数的PLF计算

虽然A型Gram-Charlier级数形式简单，计算方便，但在含有光伏等大规模间歇式新能源并网的系统中，功率波动性较大，使得随机变量的部分矩超出了该级数适用的范围，得到的概率密度曲线会出现负值。因此鉴于A型Gram-Charlier级数存在的不足，本文应用C型Gram-Charlier级数进行概率潮流计算，它采用指数的形式保证概率密度值恒大于0不会出现负值，采用归一化的方法使得概率密度函数值积分值为1，对于拟光伏出力等非正态的分布也能得到比较好的处理效果。C型Gram-Charlier级数表达式如下：

(12)

(13)

(14)

其中，Δp,q,r定义为

(15)

可简化为下式所示

(16)

ψr为Hermite矩，可表示为

(17)

对(12)式进行积分，即可得到随机变量Z的累积分布函数：

(18)

3 算法流程

考虑输入变量相关性的PLF算法流程如图1所示。

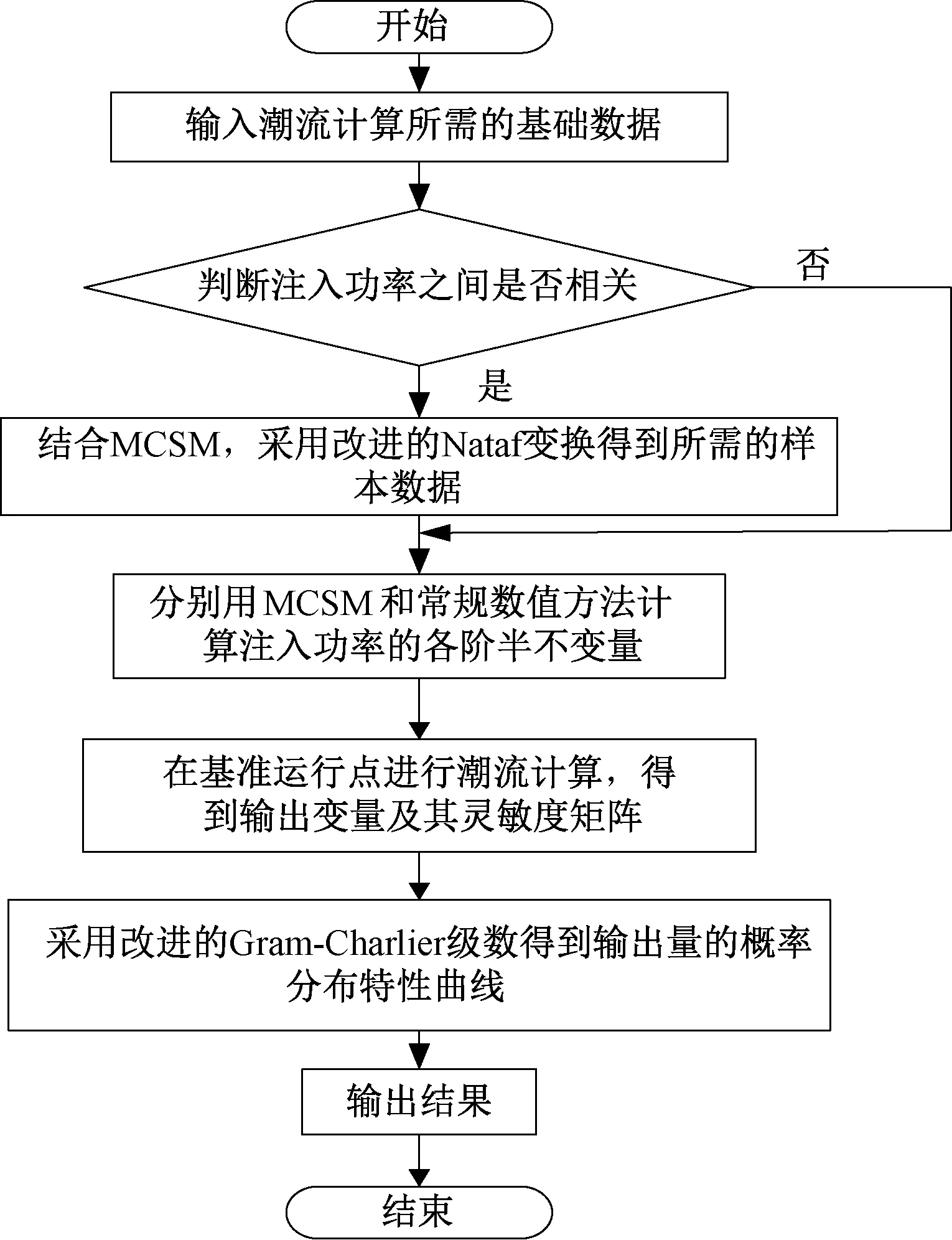
图 1 考虑输入变量相关性PLF算法流程图Fig.1 Flow chart of PLF considering correlativity of input variables

若注入的输入变量之间具有相关性，则采用MCSM生成服从标准正态分布的样本数据，再利用改进的Nataf变换技术得到输入量的数据，最后根据原点矩与半不变量的关系得到具有相关性的输入量的半不变量。若注入的输入变量之间相互独立，一般服从二项分布或正态分布，则其半不变量可以通过常规的数值方法得到。

4 算 例

4.1 IEEE14节点算例

4.1.1 算例系统说明

经过大量的抽样计算研究可知，算例采用15 000次的MCSM抽样能够很好地平衡计算精度和用时之间的矛盾，并将此结果作为“标准”结果。

本文采用MATLAB语言，在Windows环境下进行计算。仿真平台为英特尔Core i5-2450 2.5 GHZ的CPU，安装内存为4 GB。图2为IEEE14节点系统拓扑，基准功率为100 MVA，在节点10、节点13、节点14均接入装机容量为20 MW光伏电站，其中每个光伏电站光伏组件的额定功率为0.5 MW，光伏组件的个数为40。光伏电站出力采用形状系数为0.52和2.6的Beta分布。

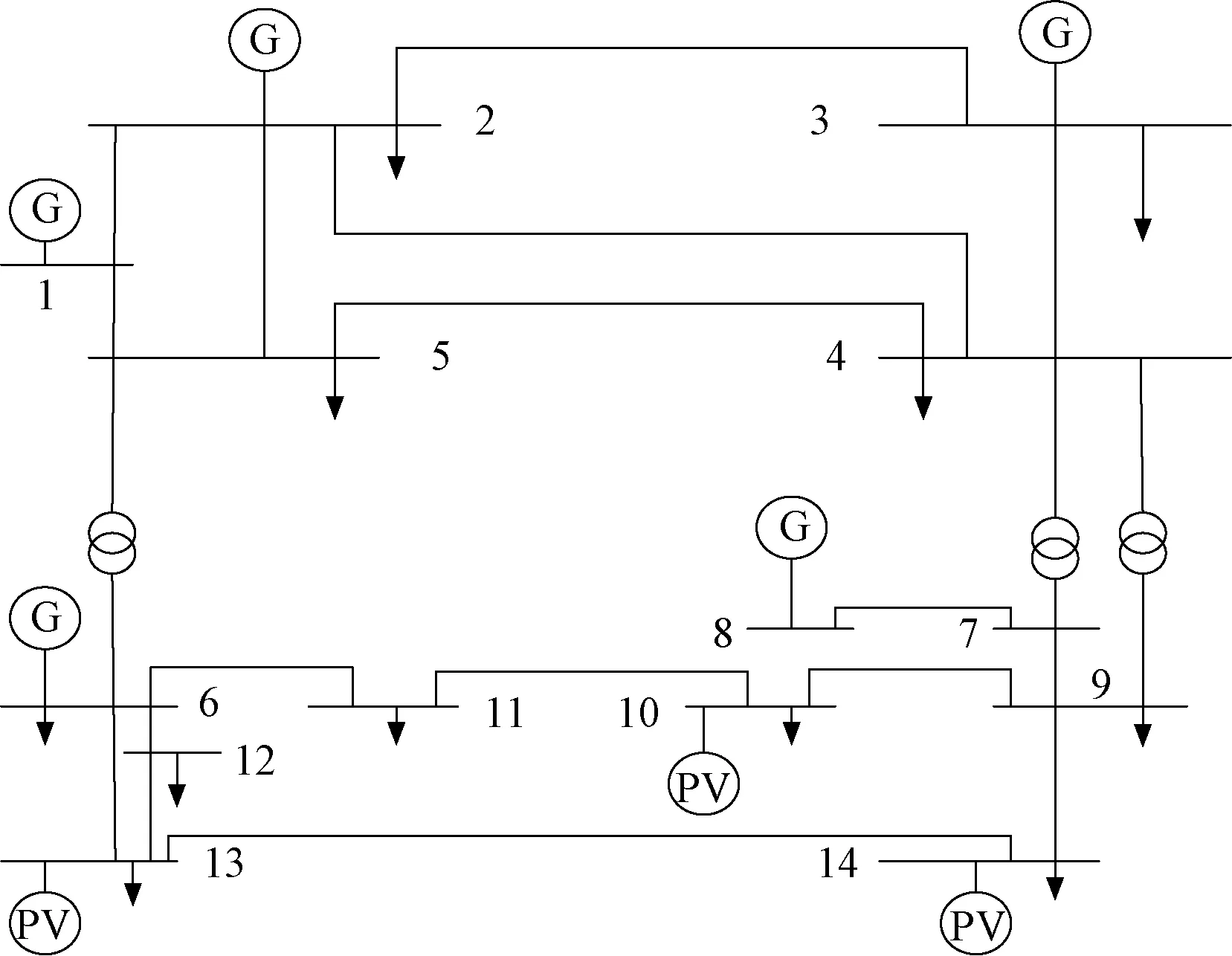
图2 IEEE14节点系统拓扑Fig.2 IEEE14 node system topology

4.1.2 算法性能评估

本文选取具有代表性的节点13电压幅值、节点13电压相角、支路12-13有功功率、支路9-14无功功率的概率分布特性曲线。本文方法与MCSM、不考虑相关性的传统CM(采用A型Gram-Charlier级数)计算所得到的概率分布特性曲线如图3所示。

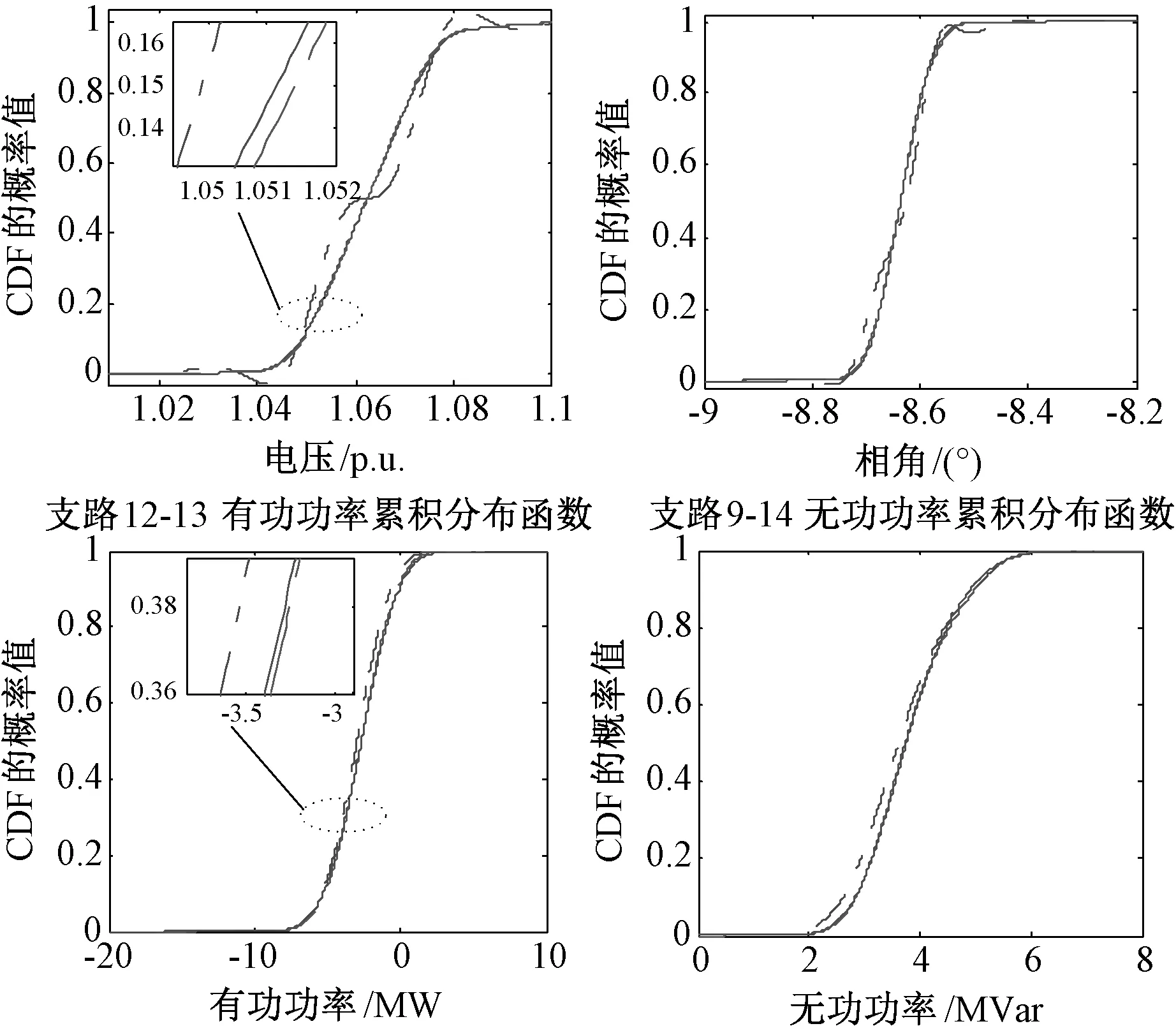
注：红色实线为MCSM，绿色虚线为本文方法，蓝色点划线为传统CM图 3 各输出量的概率分布特性曲线Fig.3 Probability distribution characteristic curves of output variables

由图3可知，当IEEE14节点系统接入具有相关性的光伏电站后，用本文提出的方法得到的概率分布特性曲线与MCSM的曲线基本一致，而不考虑相关性的传统CM与MCSM的曲线有较大的偏差。从节点13电压幅值和相角的概率分布特性曲线可以看出，传统CM概率分布特性曲线在电压幅值达到1.035 p.u.和1.08 p.u.后均出现减小的情况，相角达到-8.8°以及-8.6°后出现先增大后减小的情况，说明节点13的电压幅值和相角概率密度曲线出现负值，不满足基本的概率公理，得到不准确的结果。通过分析得到的数据可知具有相关性的大规模光伏电站并网后，系统注入量的随机性变化增强，使得该节点的三阶矩以及四阶矩超出了传统CM的适用范围，从而概率分布特性曲线出现减小的情况。说明当具有相关性的大规模光伏电站并网时，传统的CM已经不适用，而本文提出的方法没有出现这种概率密度值为负的情况，结果比较理想适用性也比较好，满足含有大规模光伏电站并网的实际情况，精度较高。

为了直观全面地验证本文方法的有效性，本文引入了输出变量期望值和标准差相对误差指标(Relativeerrorindices,REI)的概念。相对误差指标的表达式如式(19)所示：

(19)

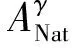
表1 输出变量的平均相对误差和最大相对误差指标(REI)Tab.1 Average relative error indices and maximal relative error indices of output variables

从表1可知输出变量期望值和标准差平均相对误差的最大值为0.918%，输出变量最大相对误差为3.254%，所有输出变量期望值和标准差的相对误差均在允许的范围内，说明本文方法在考虑光伏发电相关性的电网中具有较高的精度。

在计算效率方面，算例中各种方法的用时情况如表2所示。

表 2 不同算法用时比较

本文方法的用时要比传统CM略有增加，比蒙特卡洛方法耗时要少得多，在计算速度上有较明显的优势。从以上分析可知，本文方法能够很好地平衡计算精度和计算时间之间的矛盾，能够在较短的时间内对电网运行状态做出比较准确的评估，符合电网的实际运行的情况，从而可使运行人员能够快速准确地判断出系统运行中存在的隐患，具有实际应用推广价值。

4.2 实际电网算例

为验证本方法在实际电网中的应用效果，采用我国南方某地区2015年年末的电网网络数据进行测试。图4为南方某地区实际电网简图(该图仅画出了该电网220 kV及以上的负荷节点，以及220 kV及以上的发电机节点)，该实际电网共有437个节点，497条支路，38台发电机，以该地区电网与外电网连接的联络节点1作为平衡节点，按照该电网的实际网络数据并考虑到当地光伏电站在“十三五”规划期间的具体情况，在节点70、节点355、节点359和节点361这4个地方分别接入装机容量30 MW、30 MW、50 MW、60 MW的光伏电站。

图4 南方某地区实际电网拓扑简图Fig.4 The actual power grid topology in the south

分别应用MCSM、本文方法和传统CM对该实际电网进行PLF计算，结果如图5所示。分析可知，本文方法与MCSM所得的曲线基本一致，说明本文方法对实际电网适用性较好，而与不考虑光伏电站之间相关性的传统CM得到的曲线存在较大的误差。当大规模光伏电站并网时，实际电网情况比较复杂，各节点注入功率随机性变化较大，因而传统CM所使用的A型Gram-Charlier的缺陷表现出来，在概率密度曲线的首段末段概率密度值会出现负值，对实际电网的适用性差，不满足实际电网应用的要求，而本文提出的方法能很好地适用于实际电网，具有较强的实际应用价值。本文方法在50 s时间内可计算完成，而蒙特卡洛方法需要约2 300 s的时间，在与蒙特卡洛方法误差较小的前提下，可以节省大量的计算时间。

图 5 实际电网节点电压的概率分布特性曲线Fig.5 The node voltage probability distribution characteristic curve of the actual power grid

为了更加全面地分析本文所提方法对实际电网的应用情况，本文引入越限指标的概念，其定义如下：节点电压的低压风险概率(U<0.98 p.u.)、节点电压的低压越限概率(U<0.97 p.u.)、节点电压的高压风险概率(U>1.06 p.u.)、节点电压的高压越限概率(U>1.07 p.u.)以及支路功率的风险概率(Pn>0.7Pnmax，Pnmax为该支路传输的最大容量)、支路功率的越限概率(Pn>Pnmax)。

应用本文所提出的方法对该实际电网进行PLF计算并且用越限概率指标分析得到的潮流数据，可知各节点电压的低压风险概率和低压越限概率基本为0，部分节点高压风险和高压越限概率较为明显，支路潮流的风险和越限的概率也基本为0，部分支路出现重载。以下选取部分典型节点和支路进行分析，表3列出了部分典型节点电压风险和越限的对比情况。

表 3 部分典型节点电压越限概率对比

在分析节点电压越限情况时，本文选取具有代表性的节点57、节点89、节点106，并根据越限情况进行无功补偿。节点89并没有发生电压越限的情况，节点106虽有电压越限情况发生但越限概率较小。节点57处高压风险和越限的概率比较大，如若不进行处理将对系统运行产生不利影响，因此需要在节点处安装无功补偿设备。当在该节点处安装动态无功补偿装置时，该节点高压风险和越限概率降为6.82%和0.63%，此时补偿效果比较好，提高了系统的安全运行水平。当把考虑相关性的光伏电站接入该实际电网时，节点的相角会有1°～2°的偏移增大，同时会使得距离光伏电站较近的部分支路(例如支路50、支路253、支路275)发生潮流反向，而且支路258距离光伏电站的位置较近且初始潮流与其他支路相比较重，该支路潮流波动范围大，越限的概率也略大，因此在实际电网中应该多关注此种支路。

5 结 论

针对传统CM处理PLF方面的不足，本文提出了一种能够处理输入随机变量相关性的PLF新方法。本文所提出的方法主要有以下几个特点：

(1)采用改进的Nataf变换，能够处理不服从正态分布的随机变量之间相关性的问题，其逆变换形式比传统的Nataf变换更简单，也更实用，而且较MCSM计算速度快得多，更加符合实际电网的情况。

(2)应用C型Gram-Charlier级数，解决了含有大规模光伏电站并网的系统中概率密度值出现负值的情况，较传统CM精度更高。

(3)本文采用IEEE14节点系统和南方某地区实际电网的数据验证所提出方法的准确性和有效性，充分考虑了光伏发电相关性、负荷波动、发电机出力的随机变化等因素，大幅度地提高计算效率，同时对电网进行无功补偿，提高了安全运行水平。

[1] MIAO F,VITTAL V,HEYDT G T,et al.Probabilistic power flow studies for transmission systems with photovoltaic generation using cumulants[J].IEEE Transactions on Power Systems, 2012, 27(4): 2251-2261.

[2] BORKOWSKA B.Probabilistic load flow[J].IEEE Transactions on Power Apparatus and Systems,1974, 93(3): 752-759.

[3] 陈雁，文劲宇，程时杰.考虑输入变量相关性的概率潮流计算方法[J].中国电机工程学报，2011,31(22):80-87.

[4] 任洲洋，颜伟，项波，等.考虑光伏和负荷相关性的概率潮流计算[J].电工技术学报，2015, 30(24):181-187.

[5] 艾小猛，文劲宇，吴桐，等.基于点估计和Gram-Charlier展开的含风电电力系统概率潮流实用算法[J].中国电机工程学报，2013, 33(16): 16-23.

[6] 韩海腾，高山，吴晨，等.基于Nataf变换的电网不确定性多点估计法[J].电力系统自动化，2015,39(7): 28-34.

[7] 石东源，蔡德福，陈金富，等.计及输入变量相关性的半不变量法概率潮流计算 [J].中国电机工程学报，2012,32(28)：104-113.

[8] 郭效军，蔡德福.不同级数展开的半不变量法概率潮流计算比较分析[J].电力自动化设备，2013, 33(12):85-90.

[9] 李逸驰，孙国强，钱晓瑞，等.计及离散分布输入变量的电力系统概率潮流计算方法[J].电网技术，2015, 39(11):3254-3259.

[10] USAOLA J.Probabilistic load flow with correlated wind power injections[J].Electric Power Systems Research, 2010，80(5):528-536.

[11] 熊强，陈维荣，张雪霞，等.考虑多风电场相关性的场景概率潮流计算[J].电网技术，2015,39(8): 2154-2159.

[12] LIU P L,DER KIUREGHIAN A.Multivariate distribution models with prescribed marginals and covariances[J].Probabilistic Engineering Mechanics, 1986,1(2): 105-112.

[13] 陈璨，吴文传，张伯明，等.考虑光伏出力相关性的配电网概率潮流[J].电力系统自动化，2015,39(9)：41-47.

[14] 朱星阳，刘文霞，张建华.考虑大规模风电并网的电力系统随机潮流[J].中国电机工程学报，2013,33(7)：77-85.

[15] 周生通，李鸿光.考虑相关性的Rackwitz-Fiessler随机空间变换方法[J].工程力学，2014,31(10)：47-55.

[16] KARAKI S H,CHEDID R B,RAMADAN R. Probabilistic performance assessment of autonomous solar-wind energy conversion systems[J].IEEE Transactions on Energy Conversion, 1999, 14(3): 766-772.

Probabilistic Load Flow Calculation Considering Correlativity of Photovoltaic Generation

ZHAO Laixin，ZHAO Shuqiang，HU Yongqiang

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003,China)

The power outputs of photovoltaic (PV) generation systems located closely to each other are correlative, which will affect the accuracy of probabilistic load flow calculation. The modified Nataf transformation is adopted to handle the problems of correlation of PV generation output. Probabilistic load flow is calculated by cumulant method and C-type Gram-Charlier series. The proposed method not only has high computation efficiency compared with Monte Carlo simulation method, but also can reflect the transformation process between variable spaces. The method will effectively deal with correlation problems of PV generation outputs which do not obey the normal distribution. Meanwhile C-type Gram-Charlier series can avoid negative probability density values. The accuracy and validity of the proposed method is verified by the comparative simulation results in the IEEE 14-bus system and an actual power grid in the south.

photovoltaic (PV) generation; correlativity; probabilistic load flow; modified Nataf transformation; C-type Gram-Charlier series

10.3969/j.ISSN.1007-2691.2017.02.10

2016-06-11.

中央高校基本科研业务费专项资金资助项目(2015MS94).

TM744

A

1007-2691(2017)02-0068-07

赵来鑫(1990-)，男，硕士研究生，研究方向为电力系统运行、分析与控制；赵书强(1964-)，男，教授， 博士生导师，研究方向为电力系统稳定分析和控制、电力系统规划与可靠性等；胡永强(1981-)，男，讲师，博士研究生，研究方向为电力系统运行、分析与控制以及新能源发电与智能电网。