感性负载条件下IGBT开通过程分析
2017-04-21唐新灵李金元
唐新灵,崔 翔,张 朋,李金元,赵 哿
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206;2.全球能源互联网研究院,北京 102209)
感性负载条件下IGBT开通过程分析
唐新灵1,崔 翔1,张 朋2,李金元2,赵 哿2
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206;2.全球能源互联网研究院,北京 102209)
针对IGBT的开通过程中,研究了感性负载条件下IGBT的开通过程中栅极电压、集电极电流、集射极电压随时间变化的特点及其相互关系。详细阐述了栅极电容随栅极电压变化的机理以及栅极平台电压产生的机理,分析了驱动电阻对栅极电压的影响。根据IGBT开通电流特点,提出用二次函数来拟合IGBT开通时的集电极电流波形,同时还分析了主回路杂散电感对开通波形的影响。搭建了IGBT动态开关特性测试平台,测量结果验证了本文分析的正确性。
IGBT;感性负载;开通过程
0 引 言
绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)具有电压控制、开关速度快以及通态损耗低等优点[1],被广泛应用于高压大容量变频器[2-4]、直流输电等领域[5-7]。IGBT芯片经历了由穿通型(Punch Through,PT)、非穿通型(Non Punch Through,NPT)到场终止型(Field Stop, FS)的发展过程[8];为了满足应用需求,IGBT封装在发展焊接形式的同时,结合了IGBT与GTO的共同优点,发展了大功率的压接封装形式[9,10]。
随着载流子寿命控制等技术的应用,IGBT关断损耗得到了明显改善;此外,大功率IGBT器件内部续流二极管的反向恢复过程,极大地增加了IGBT的开通损耗,因此,IGBT的开通过程越来越引起重视。准确的IGBT开通模型,可以用于仿真分析IGBT在不同工况条件下的开关波形,对器件的开通损耗、可能承受的电气应力、电磁干扰噪声等进行评估,为驱动电路进行优化提供指导,从而改善IGBT的开通特性[11,12]。
目前广泛应用的IGBT开关模型主要有解析模型[13]和集总电荷模型[14,15]。解析模型基于双极输运方程、大注入假设以及非准静态效应,定性地描述了IGBT的开关特性。集总电荷建模的方法是在电极之间建立电容与电荷模型,基于电容充放电的原理,研究开关过程中的电压与电流关系。上述方法都可以用于IGBT开关建模,但是对于IGBT开通机理缺少详细地分析,不能描述开通过程中集射极电压、集电极电流随栅极电压变化的关系。
鉴于上述方法的局限性,文献[16]结合了开通过程中驱动回路的电容充电模型,分阶段地分析了IGBT的开通波形,对于理解IGBT开通特性具有重要的意义。但是,文中没有对每个阶段电容的形成原因进行分析,也没有解释密勒平台产生的机理,同时缺少栅极电压与集射极电压的相互影响分析。文献[17,18]也分析了开通过程中集电极电流、集射极电压与栅极电压的相互关系,但是都采用的是电路方法,缺少对开通波形产生机理的分析,同样存在与文献[16]相似的问题。
本文针对感性负载条件下的IGBT开通过程,从IGBT阻断状态下的空间电荷分布开始分析,研究了IGBT输入电容随栅极电压变化的关系,揭示了栅极电压密勒平台形成的机理,分析了驱动电阻对栅极电压波形的影响。研究了IGBT集电极电流的上升特点;分析了IGBT集射极电压的下降特点,揭示了回路杂散电感对集射极电压的影响规律。最后,搭建了IGBT动态特性测试平台,获得了IGBT开通波形,梳理了开通过程各个阶段中栅极电压、集电极电流、集射极电压的相互关系;基于实验测量了不同阻值下的栅极电压波形、不同回路杂散电感条件下的集射极电压波形,也对测量所得的开通波形进行了曲线拟合,实验结果验证了本文分析的正确性。
1 IGBT基本结构
IGBT芯片横截面的基本结构如图1(a)所示。图中的P+和N+表示集电区和源区为重掺杂,N-表示基区掺杂浓度较低。相对于功率MOSFET而言,IGBT在结构上多了一层P+衬底,即图1(a)所示的P+集电区。因此,IGBT在流过电流时,既有少数载流子参与,也有多数载流子参与,由于电导调制效应,IGBT通态压降相对于相同结构的MOSFET要低得多。
由图1(a)可知,单个IGBT元胞内包括一个MOSFET,一个PNP晶体管和一个NPN晶体管。PNP晶体管集电极(P基区)与NPN晶体管发射极(N+源区)之间的电压降用等效电阻Rs表示,当Rs足够小时,NPN晶体管的影响可以忽略不计。通常情况下,IGBT的等效电路模型如图1(b)右图所示。
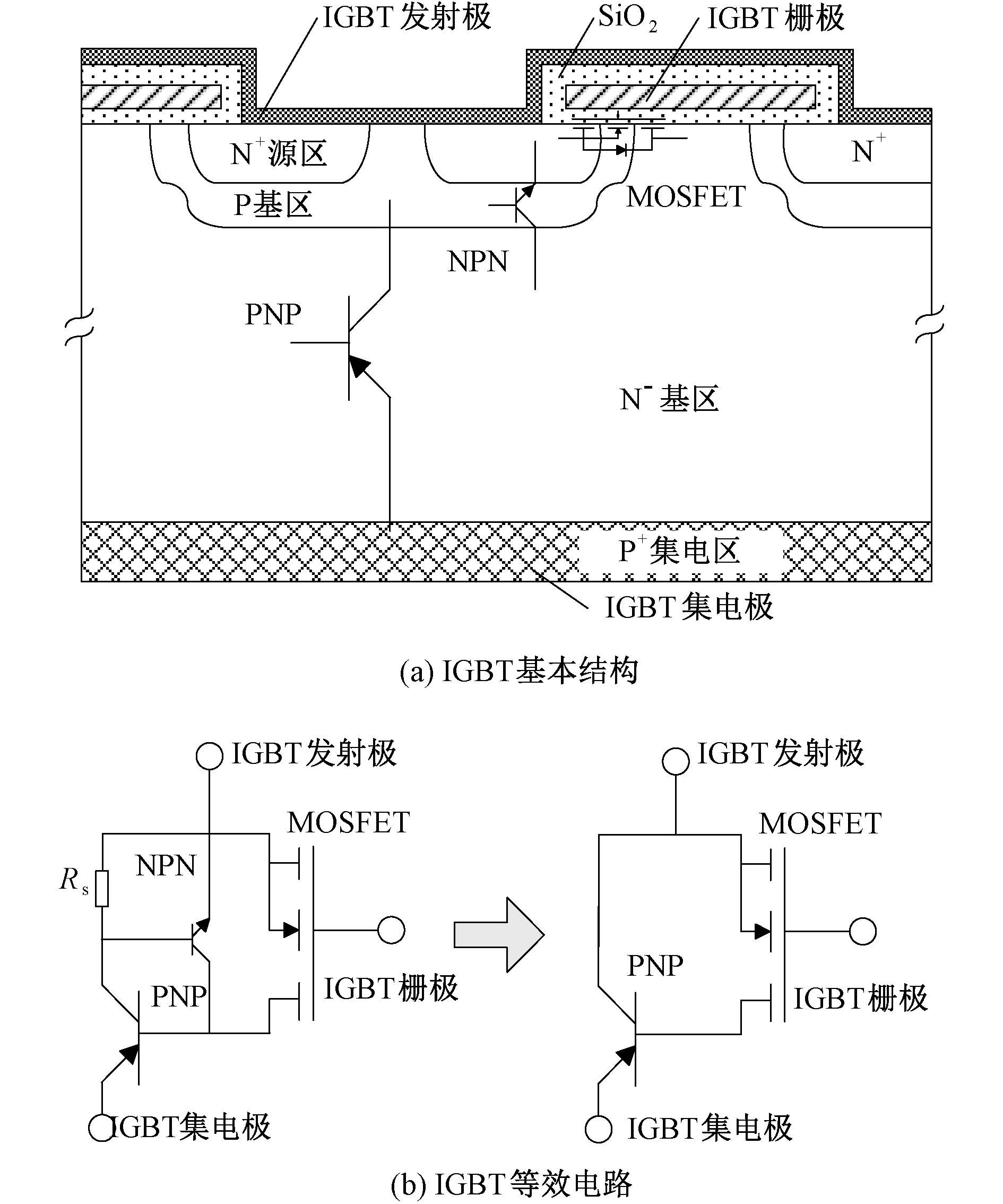
图1 IGBT基本结构及其等效电路Fig.1 IGBT structure and equivalent circuit
2 开通过程中的栅极电压分析
2.1 关断状态分析
由图1(a)可知,IGBT内部有三个PN结,即P+集电区和N-基区之间的PN结J1,N-基区和P基区之间的PN结J2,P基区和N+源区之间的PN结J3。由于P基区的厚度相对于整个IGBT的厚度来说,可以忽略不计,因此本文采用一维模型进行分析,如图2所示。

图2 关断状态下IGBT耗尽区电场分布Fig.2 Electric field distribution in space charge area of IGBT during off-state
假设器件承受的阻断电压为VR,则N-基区和P基区的耗尽区总宽度为[19]
(1)
式中:Vbi为J2的内建电势;Na为P基区掺杂浓度;Nd为N-基区掺杂浓度,且满足
(2)
考虑到实际掺杂浓度Na≫Nd,从而可以得到PN结J2的耗尽区宽度为
(3)
公式(3)中的Wbcj就是关断状态下IGBT低掺杂基区耗尽区的宽度。
2.2 开通延迟过程
2.2.1 IGBT栅极电容组成
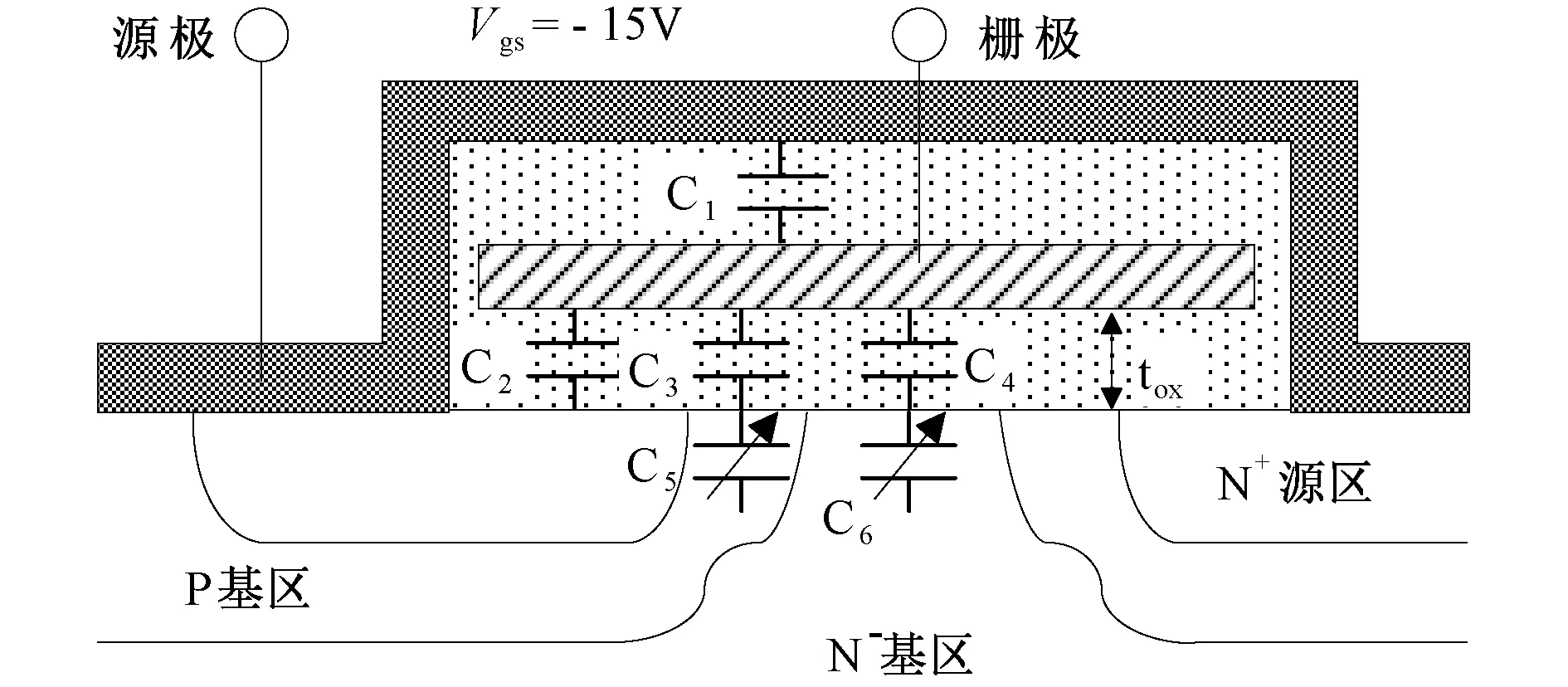
图3 IGBT栅极电容分布Fig.3 Gate capacitance of IGBT
对于IGBT器件,栅极电容包括四个方面电容,如图3所示:(1)栅极—发射极金属电容C1;(2)栅极—N+源极氧化层电容C2;(3)栅极—P基区电容Cgp,Cgp由C3,C5构成;(4)栅极—集电极电容Cgc,Cgc由C4,C6构成。其中,栅极—发射极电容(也称为输入电容)为Cge=C1+C2+Cgp,栅极—集电极电容(也称为反向传输电容或密勒电容)为Cgc。此外,Cgp随栅极电压的变化而变化,Cgc随IGBT集射极电压的变化而变化。
2.2.2 栅极电压对输入电容的影响
由图3可知,C5是IGBT中MOSFET结构的MOS电容,该电容是直流栅压的函数。对于p型衬底MOS电容,栅极电压变化时,各个阶段的电容特性及其大小如下[18]:
当栅极电压为负值时,MOS电容开始工作在堆积模式,此时的栅极—P基区的单位面积电容为
(4)
随着电压的增加,逐步形成耗尽区。耗尽模式下的栅氧化层电容与耗尽层电容是串联的,此时栅极—P基区的单位面积电容为
(5)
栅极电压继续增加,当栅极电压大于阈值电压,耗尽宽度达到最大并逐步形成反型层。由于IGBT的开关速度相对较慢,反型层电荷能够跟上电容电压的变化,此时的栅极—P基区电容为
(6)
式中:ξox为栅氧化层介电常数;tox为栅氧化层厚度;ξs为硅介电常数;xd为耗尽区宽度;xdT为反型转变点时的最大空间电荷宽度。
根据上述分析,电容Cgp的变化趋势如图4所示。因此,Cgp随着电压的增加,其电容值先减小,随着电压的进一步增加,其大小又逐渐增加,并达到稳定值。

图4 IGBT中MOS沟道电容与栅压的关系Fig.4 Relationship between MOS channel capacitance and gate voltage in IGBT
2.2.3 开通延时过程中驱动回路等效电路
由于在IGBT集电极电流上升之前,IGBT仍然处于关断状态,栅极电压的变化量相对于IGBT的阻断电压可以忽略不计。因此,栅极电压的上升过程对于栅极—集电极电容(Cgc)及其电荷量的影响可以忽略不计,因此开通延时阶段的充电过程只针对电容C1、C2和Cgp。因此,结合驱动回路的等效电路,可以得到上述充电过程中驱动回路的等效电路如图5所示,其中Vg为栅极驱动板输出电压,Rg为驱动电阻,Cin为驱动板输出端口电容,Rs和Ls分别为驱动回路寄生电阻和寄生电感。栅极电压开始上升一段时间后达到阈值电压,集电极电流开始上升,这个过程也称之为开通延迟。

图5 开通延迟过程中的驱动回路等效电路图Fig.5 Equivalent circuit of gate drive in opening delay
基于上述分析可知,栅极电压在到达阈值电压之前,输入电容并不是恒定值,而是有一个由大逐渐变小,再逐步增大的过程。因此,在IGBT开通过程中,驱动回路并不是给恒定电容充电。图6给出了变电容情况下栅极电压上升过程,其中实线为给恒定电容时的电压曲线,虚线为考虑输入电容变化时的电压曲线。

图6 开通过程栅极电压上升趋势Fig.6 Gate voltage rising curve during opening delay
2.3 密勒平台过程
2.3.1 密勒平台过程形成机理
栅极电压在上升到一定值后,会有一个栅极电压维持水平的阶段,这个电压称之为密勒平台电压。为了便于分析密勒平台的形成过程,本文对IGBT模型进行了简化,如图7所示,图中C′为开通过程中耗尽区与中性基区分界面上的点。
由上一节分析可知,当栅极电压大于阈值电压,IGBT开始通过正向电流。当集电极电流达到最大电流时,续流二极管反偏,IGBT两端的电压Vce迅速降低,耗尽区迅速缩减,Vds的电压也随之降低,而耗尽区缩减以及电压Vds降低的过程决定了栅极电压密勒平台的形成过程。
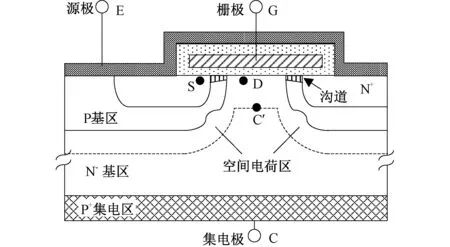
图7 IGBT简化模型Fig.7 Simplified model of IGBT
耗尽区消失前,当Vds满足Vds+VTd>Vgs时,单位面积的栅极—集电极电容为
(7a)


图8 密勒电容及其所带电荷分析Fig.8 Miller capacitance and charge distribution
随着IGBT集射极电压Vce的减小,当Vds满足Vds+VTd
(7b)
随着中性基区电导调制范围的扩大,Vce进一步减小,且Vds (7c) 此时的电容模型如图8(c)所示。图8(b)和图8(c)的电容大小一致,两个图的区别在于电容带电的极性不一样,这表示了基区电压下降时,电容Cgc带电量变化的过程。上述Vce变化的过程中,驱动回路的等效电路如图9所示。 图9 栅极电压平台阶段驱动回路等效电路图Fig.9 Equivalent circuit of gate drive during gate voltage plateau 图9中的栅极—集电极电容Cgc是一个电容值和带电量都变化的过程,其变化过程不由栅极电压控制,而是由变化的集射极电压决定。在这个过程中,驱动回路一直给电容Cgc进行充电,栅极电压Vg不上升的原因在于电压Vce一直在减小,这也是密勒平台形成的直接原因,这个过程中驱动回路只给Cgc电容充电,驱动回路的等效电路如图9所示。 在Vce下降后,米勒平台继续维持的原因在于此时的载流子浓度在持续增加,因此电容值也在增加,从而栅极电压仍然维持在密勒平台电压。 2.3.2 栅极电压由上升过程到密勒平台的过渡 根据上述分析可知,IGBT开通以后,驱动回路给输入电容充电,栅极电压逐步上升。当IGBT开通后,电流达到最大值,续流二极管承受反向电压,此时IGBT耗尽区宽度急剧降低。耗尽区宽度减小的过程对应于图8(a)电容放电的过程。 考虑到驱动回路电阻不为零,如果驱动回路的充电速度跟不上电容Cgc的放电速度,那么电容C1、C2以及Cgp会在耗尽区迅速缩小的短暂时间内向Cgc充电,从而导致栅极电压会有略微降低,如果Cgc的值较大,当驱动回路满足一定条件时[20],甚至有可能引起栅极电压的振荡。 耗尽区消失后驱动回路继续给电容Cgc充电。这个过程中,随着基区电导调制区的扩大,Vds的值继续降低,栅极电压基本保持不变。 2.4 栅极电压继续上升过程 栅极电压平台阶段结束后,驱动回路继续给Cgs和Cgc同时充电,栅极电压开始上升。此时单位面积的栅极—集电极电容为 (8) 图10 驱动回路等效电路图Fig.10 Equivalent circuit of gate drive 在这个阶段,输入电容包括四个部分:(1)栅极—发射极金属电容C1;(2)栅极—N+源极氧化层电容C2;(3)栅极—P基区电容C3;(4)栅极—集电极电容C4;充电的等效电路如图10所示。因此,在这个阶段中,电压上升的速度要慢于开通延迟阶段。 2.5 驱动电阻对栅极电压波形的影响 上述分析了IGBT在开通过程中栅极电压的变化过程,并给出了对应的等效电路。根据上述分析,由图5、在给栅极电容充电的阶段,驱动电阻的值越小,时间常数越小,从而栅极电压上升越快,开通延迟的时间越短。由图9可知,驱动电阻越小,相同的栅极平台电压值,平台持续时间也越短。由图10可知,驱动电阻越小,平台电压之后,上升到最大栅极电压的时间也越短。 3.1 开通电流 栅极电压小于开通阈值电压之前,IGBT处于关断状态;栅极电压一旦大于阈值电压,N+源区的电子通过MOS沟道流向N-基区,集电极电流开始上升。由于此时耗尽区仍然存在,因此根据图7所示的模型,可知 其中 那么此时流过MOSFET的电流,也就是IGBT的集电极电流为 (9) 由于集电极电流上升速度极快,因此在集电极电流由零上升到负载电流这一短时间内,栅极电压可以近似认为是线性增长,从而IGBT集电极电流在到达负载电流之前,可以认为IGBT集电极电流曲线为二次函数曲线,即 (10) 其中a由芯片参数以及功率回路参数、驱动回路参数共同决定。 3.2 二极管反向恢复过程 IGBT集电极电流过冲与续流二极管的反向恢复过程相对应。IGBT集电极电流持续增大的过程中,续流二极管中的少子浓度逐渐降低,反偏电流密度梯度也逐渐减小。当续流二极管达到反偏电流的最大值,二极管中耗尽区边缘少子浓度达到热平衡浓度。此后,二极管进入反向恢复阶段,此时的IGBT集电极电流特性更多地取决于续流二极管的反向恢复特性,因为这个过程中需要将二极管中余下的过剩载流子移除,且耗尽区的电势降大小为反偏电压值。通常情况下,为了使二极管快速关断,需要有较大的反偏电流和较小的少子寿命。 4.1 集射极电压下降过程分析 理想条件下,不考虑回路中的杂散电感和电阻,当续流二极管的电流达到最大反向电流时,二极管开始承受反向电压,此时IGBT两端的电压急剧下降。IGBT集射极电压下降包括两个阶段,第一个阶段类似于MOSFET开通机理,耗尽区迅速消失,电压急剧下降,如图11所示的UCE_MOSFET阶段;第二个阶段是过剩载流子在基区内扩散,电导调制区扩大,中性基区压降减小过程,如图11所示的UCE_BJT阶段。由于载流子扩散的速度远远慢于耗尽区消失的速度,因此这个阶段的电压衰减非常缓慢。 图11 理想条件下IGBT开通电压波形Fig.11 Ideal turn-on voltage waveforms of IGBT 4.2 杂散电感对电流上升阶段Vce的影响 感性负载双脉冲测试电路如图12所示,负载电感足够大,在开通过程中,负载电感的电流大小基本不变。理想条件下,续流二极管承受反向电压时,IGBT集射极电压开始下降。 图12 感性负载条件下IGBT开通测试电路Fig.12 Circuit for IGBT inductive turn-on 但是,实际工况条件下,主回路中存在一定的杂散电感。因此,在集电极电流上升过程中,二极管处于正向大电流偏置状态,其通态压降可以忽略不计,从而可以得到如下关系式: (11) 式中:Vce为IGBT器件集射极电压;Ls为主回路杂散电感;ic为IGBT的集电极电流;Vdc为直流母线电压。因此,从电流上升的时刻开始,IGBT器件两端的电压就低于直流母线电压。即 (12) 结合式(16)可以得到 (13) 由上式可知,集电极电流上升过程中,集射极电压近似线性下降;且杂散电感越大,集射极电压下降速度越快。 5.1 测试平台 为了验证本文分析的正确性,基于如图12所示的电路原理,搭建了如图13所示的压接式IGBT动态参数测试平台。被测IGBT为WESTCODE公司的T0600TB45A(4.5 kV/600 A),施加在IGBT上的机械压力大小为10 kN,压力误差为5%。续流二极管采用的是DYNEX公司的IGBT模块,型号为DIM800NSM33-A00,实验温度为室温。 示波器型号为TekTronix DPO4104B,带宽1 GHZ,采样率5 GS/s;栅极电压探头型号为TPP0500,带宽500 MHz,探头延时5.3 ns;集射极电压探头型号为THDP0100,带宽100 MHz,探头延时16.7 ns;电流探头的采用PEM罗氏线圈,带宽12 MHz,探头延时30.2 ns。在对IGBT进行测试前需要对电压、电流探头进行延时补偿,保证测量的准确性。 图13 压接型IGBT测试平台Fig.13 Test platform for Press Pack IGBT 5.2 测试结果与分析 使用图13所示的测试平台,可以测量得到IGBT的开通波形如图14所示,并将图中的IGBT开通过程分为5个阶段。其中VG(off)为关断状态的负栅极电压,VG(on)为开通状态的正栅极电压。VGE为栅极实时测量电压,VG(th)为IGBT开通阈值电压,VDC为直流母线电压,IL为负载电流,IRR为二极管反向恢复最大电流,IC为IGBT集电极电流,VCE为IGBT集射极电压。 图14 IGBT开通电流波形Fig.14 IGBT turn-on waveforms 阶段1:开通延迟阶段 在这个阶段中,驱动回路给输入电容充电,栅极电压逐步增加,当栅极电压到达阈值电压以后,IGBT开通,集电极电流开始增加。需要指出的是,阶段1所示虚线圆圈内的栅极电压有一个斜率增加的过程,对应于栅极电压在上升的过程中,栅极输入电容变化的过程。 阶段2:电流上升阶段 在这个阶段中,MOSFET沟道导通,由于电流上升速度非常快,短时间内栅极电压近似线性增长。当集电极电流IC小于负载电流时,IC可以用开口向上的二次函数拟合,此时的集射极电压随着集电极电流的增加而线性减小。 阶段3:集射极电压迅速下降过程 当IGBT集电极电流IC大于峰值电流IL+IRR以后,续流二极管承受反向电压,电流迅速减小,从而IGBT的电流也迅速减小。 续流二极管在承受反向电压以后,IGBT的集射极电压迅速降低,耗尽区也迅速消失。耗尽区缩小的过程引起了栅极—集电极电容及其所带电荷量的迅速变化,如第二节所分析,栅极电压从而进入密勒平台阶段。 值得注意的是,从第2阶段到第3阶段,由于集射极电压的迅速下降,栅极电压Vge有一个电压跌落的过程,这与2.3.2节的分析基本一致。 阶段4:栅极平台阶段 这个阶段的特征之一是IGBT电流的衰减过程,这由续流二极管的反向恢复特性决定。其次,IGBT集射极电压VCE继续减小,这是由于开通后IGBT内电导调制区的扩大所引起。在这个过程中,靠近栅极侧的中性基区电势Vds不断降低,栅极电压的值基本不变。 阶段5:栅极电压继续上升阶段 这个过程中,驱动回路继续给栅极电容充电,IGBT集射极电压基本达到稳定通态压降,IGBT集电极电流等于负载电流。 5.3 驱动电阻对栅极电压的影响 为了验证本文第二节中,驱动电阻对栅极电压的影响分析,对不同驱动电阻条件下的栅极电压波形以及IGBT集电极电流波形进行了比较,如图15所示。 图15 驱动电阻对开通波形的影响Fig.15 Turn-on waveforms under different gate resistance 由图15(a)可知随着驱动电阻的增加,栅极电压上升的速度减小,栅极平台电压持续时间增加;平台电压过程结束后,栅极电压上升的速度更慢。图中虚线圆圈内,表明栅极电压上升速度的变化,验证了本文中对栅极—发射极电容分析的正确性。由图15(b)可知,随着驱动电阻的增加,电流开通延迟时间增加,上升速度变慢,但是开通电流过冲更小。 5.4 IGBT开通电流波形的拟合 针对图14所示的IGBT开通电流波形,选取电流0 对于各个阶次的拟合,其拟合结果与实际测量电流的误差如图17所示。由图17可知,线性函数拟合结果存在很大的误差,二次函数拟合基本可以描述开通的集电极电流波形,三阶及以上的高阶次多项式拟合,可以达到较高的精度。因此,本文所提出的二次函数拟合方法可以较为准确地描述IGBT开通电流波形。 图16 开通波形拟合Fig.16 Fitting curves of turn on current 图17 拟合误差Fig.17 Relative error of fitting curves 5.5 回路杂散电感对开通电压的影响 为了研究杂散电感对IGBT开通过程中集射极电压的影响,测量了IGBT器件在不同回路杂散电感条件下的开通波形,测量结果如图18所示。 由图18可知,相同驱动条件下,随着主回路杂散电感Ls值的增加,IGBT器件开通电流上升速度略有减小。但是,集射极电压下降的速度却非常明显,且平台电压的值更低。因此,杂散电感对于集射极电压降低起到了非常重要的作用,这与本文分析的结论相一致。同时,由图18可以得知,主回路杂散电感的值越大,IGBT的开通损耗越低。 图18 杂散电感对开通过程集射极电压的影响Fig.18 Collector-emitter voltage under different stray inductances 本文针对IGBT开通过程中的物理机理,分析了IGBT在感性负载条件下的开通过程,梳理了栅极电压、集电极电流、集射极电压的相互关系,并得到如下结论: (1)栅极电压达到阈值电压之前,随栅极电压的升高,栅极—发射极电容Cge先减小,后增大。 (2)密勒平台形成的原因在于集射极电压降低引起的电容和带电量发生变化。 (3)驱动电阻越小,栅极电压上升越快,开通延迟时间越短,勒平台持续时间越短。 (4)IGBT集电极电流线性拟合误差较大,可以采用二次函数进行拟合。 (5)主回路杂散电感越大,IGBT开通过程中集射极电压初始下降速度越快,IGBT的开通损耗越小。 [1] FILSECKER F, ALVAREZ R, BERNET S. Comparison of 4.5-kV press pack IGBTs and IGCTs for medium-voltage converters[J]. IEEE Transactions on Industrial Electronics,2013,60(2):440-449. [2] 于华龙,鲁挺,姬世奇,等. 高压IGBT串联均压控制电路阈值电压设计方法[J]. 中国电机工程学报,2016,36(5):1357-1365. [3] 孟庆云,晏明,潘启军,等. 一种适用于大容量重点钳位型三电平逆变器的绝缘栅双极型晶体管吸收电路研究[J]. 中国电机工程学报,2016,36(3):755-764. [4] 丁杰,张平. IGBT水冷散热器实验与仿真[J]. 华北电力大学学报(自然科学版),2015,42(1):97-103. [5] ASPLUND G, ERIKSSON K, SVENSSON K. DC Transmission based on voltage source converters[C]//CIGRE SC14 Colloquium, South Africa, 1997:1-7. [6] SANO K, TAKASAKI M. A surgeless solid-state DC circuit breaker for voltage-source-converter-based HVDC systems[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2690-2699. [7] 徐延明,赵成勇,徐莹,等. IGBT模块电气模型及实时仿真研究[J]. 华北电力大学学报(自然科学版),2016,43(2):8-16. [8] VOLKE A, HORNKAMP M. IGBT Modules[M]. Munich: Infineon Technologies AG, 2012:46-49. [9] SHIGGEKANE H, KIRIHATA H, UCHIDA Y. Developments in modern high power semiconductor devices[C]//Proceedings of the 5thInternational Symposium on Power semiconductor Devices and ICs, 1993:16-21. [10] EICHER S, RAHIMO M, TSYPLAKOV E, et al. 4.5kV press pack IGBT designed for ruggedness and reliability[C]//Proceedings of the 39thIAS Annual Meeting on Industry Applications Conference, Oct.2004: 1534-1539. [11] 孟进,马伟明,张磊,等. 基于IGBT开关暂态过程建模的功率变流器电磁干扰频谱估计[J]. 中国电机工程学报,2005,25(20):16-20. [12] HEFNER A R. Analytical modeling of device-circuit interactions for the power insulated gate bipolar transistor (IGBT)[J]. IEEE Transactions on Industry Applications, 1990,26(6):995-1005. [13] HEFNER A R, BLACKBURN D L. An analytical model for the steady-state and transient characteristics of the power insulated-gate bipolar transistor[J]. Solid-State Electronics, 1988, 31(10):1513-1532. [14] BUDIHARDJO I, LAURITZEN P O. The Lumped-Charge power MOSFET model, including parameter extraction[J]. IEEE Transactions on Power Electronics, 1995,10(3):379-387. [15] LAURITZEN P O, ANDERSEN G K, HELSPER M. A basic IGBT model with easy parameter extraction[C]//in Proc. PESC, Vancouver, BC, Canada, Jun.2001:2160-2165. [16] BRYANT A T, LU Liqing, SANTI E, et al. Modeling of IGBT resistive and inductive turn-on behavior[J]. IEEE Transactions on Industry Applications, 2008,44(3):904-914. [17] GRBOCIC P J, GRUSON F, IDIR N, et al. Turn-on Performance of reverse blocking IGBT (RB IGBT) and optimization using advanced gate driver[J]. IEEE Transactions on Power Electronics, 2010,25(4): 970-980. [18] FENG H, YANG W, ONOZAWA Y, et al. Transient turn-on Characteristics of the Fin p-Body IGBT[J]. IEEE Transactions on Electron Devices, 2015,62(8): 2555-2561. [19] Donald A. Neamen. 半导体物理与器件[M]. 北京:电子工业出版社,2013:280-282. [20] 邓夷,赵争鸣,袁立强,等. 适用于复杂电路分析的IGBT模型[J]. 中国电机工程学报,2010,39(9): 1-7. Analysis on IGBT Turn-on Transient Under Inductive Load TANG Xinling1, CUI Xiang1, ZHANG Peng2, LI Jinyuan2, ZHAO Ge2 (1. State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources, North China Electric Power University,Beijing 102206, China; 2.Global Energy Interconnection Research Institute,Beijing 102209, China) In the turn-on process of insulated gate bipolar transistor (IGBT), under the inductive load condition, the gate voltage, collector current and emitter voltage vary with time, and the changing characteristics and their relationships are analyzed in this paper. A detailed description of mechanism of gate voltage-dependent gate capacitance and generation mechanism of gate voltage plateau is given in this paper and the influence of driving resistance on gate voltage is analyzed. A quadratic function is proposed to fit collector current curve based on the characteristic of collector current during the turn-on transient. The impacts of stray inductance in major circuit on turn-on waveforms are studied. Experimental results of IGBT dynamic switch characteristics test platform verified the accuracy of the analysis in this paper. IGBT; inductive load; turn-on transient 10.3969/j.ISSN.1007-2691.2017.02.05 2016-08-26. 国家重大科技专项02专项(2015ZX02301). TM 85 A 1007-2691(2017)02-0033-09 唐新灵(1988-),男,博士研究生,研究方向为电力系统自动化技术,柔性直流输电用大功率半导体器件研究;崔翔(1960-),男,教授,博士生导师,研究方向为电力系统电磁环境和电磁兼容。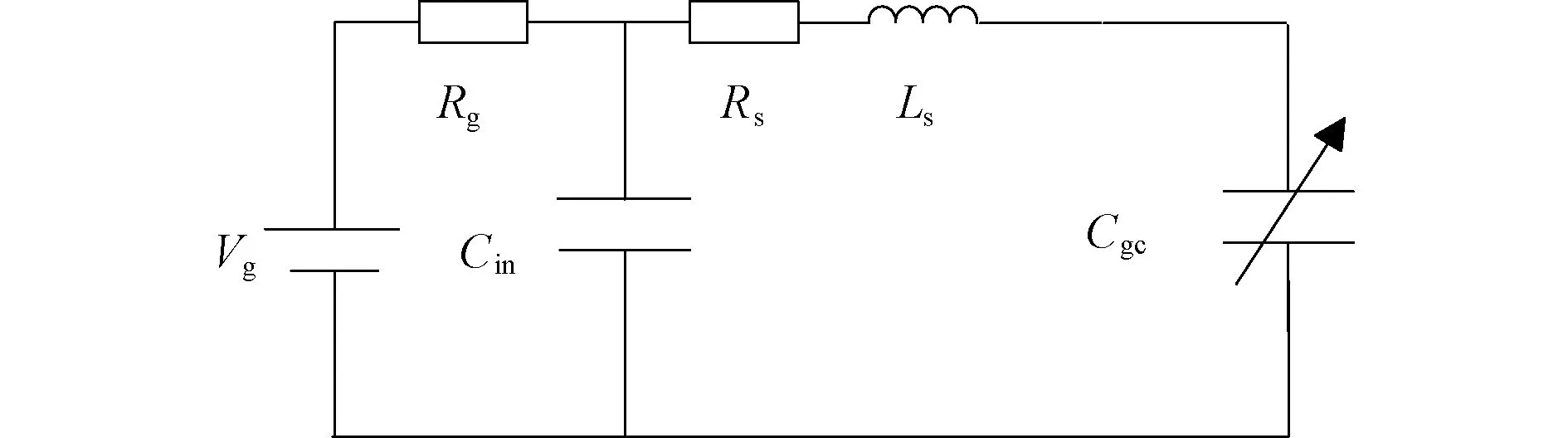

3 开通过程中的集电极电流分析
4 开通过程中的集射极电压分析
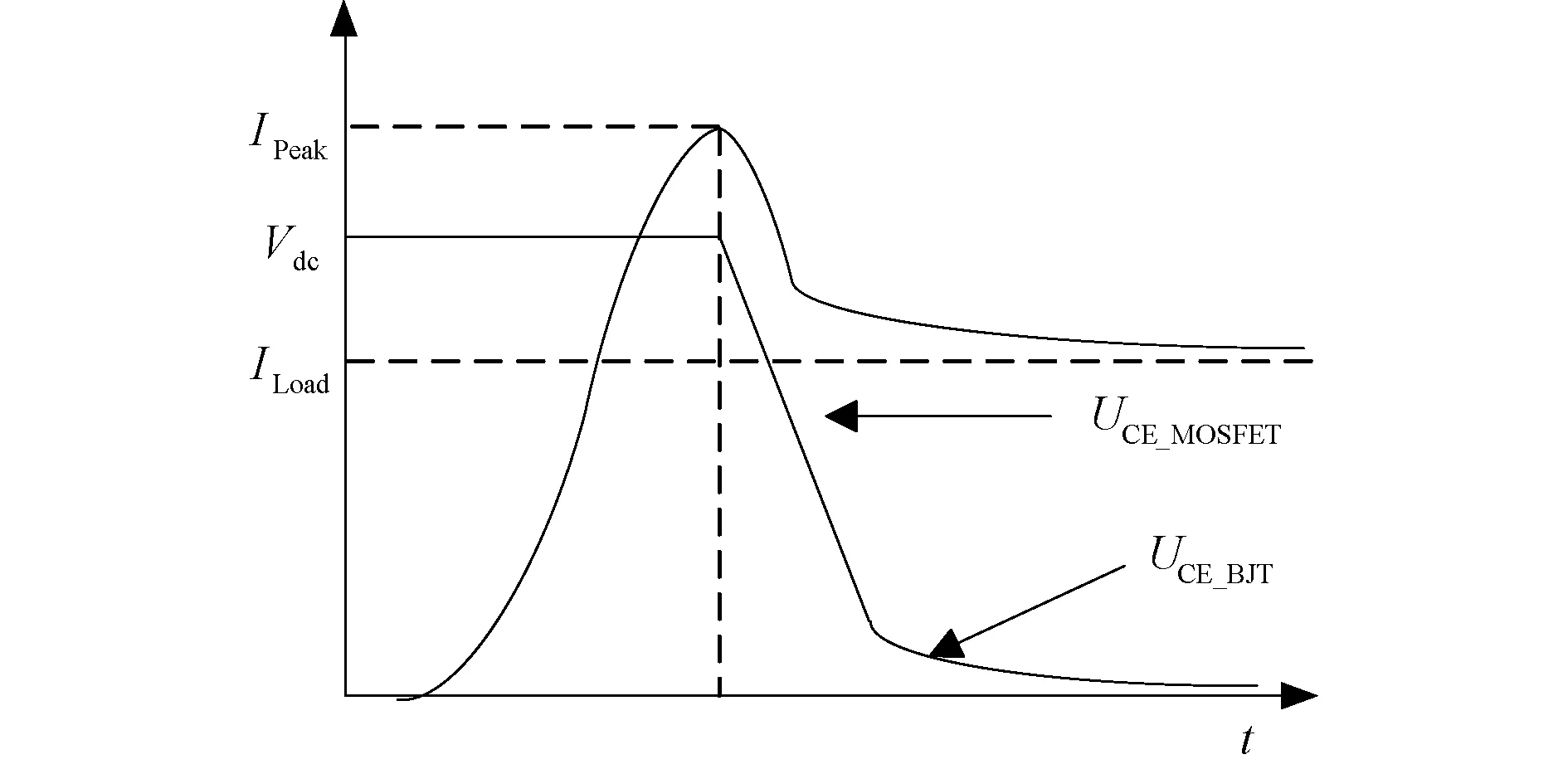
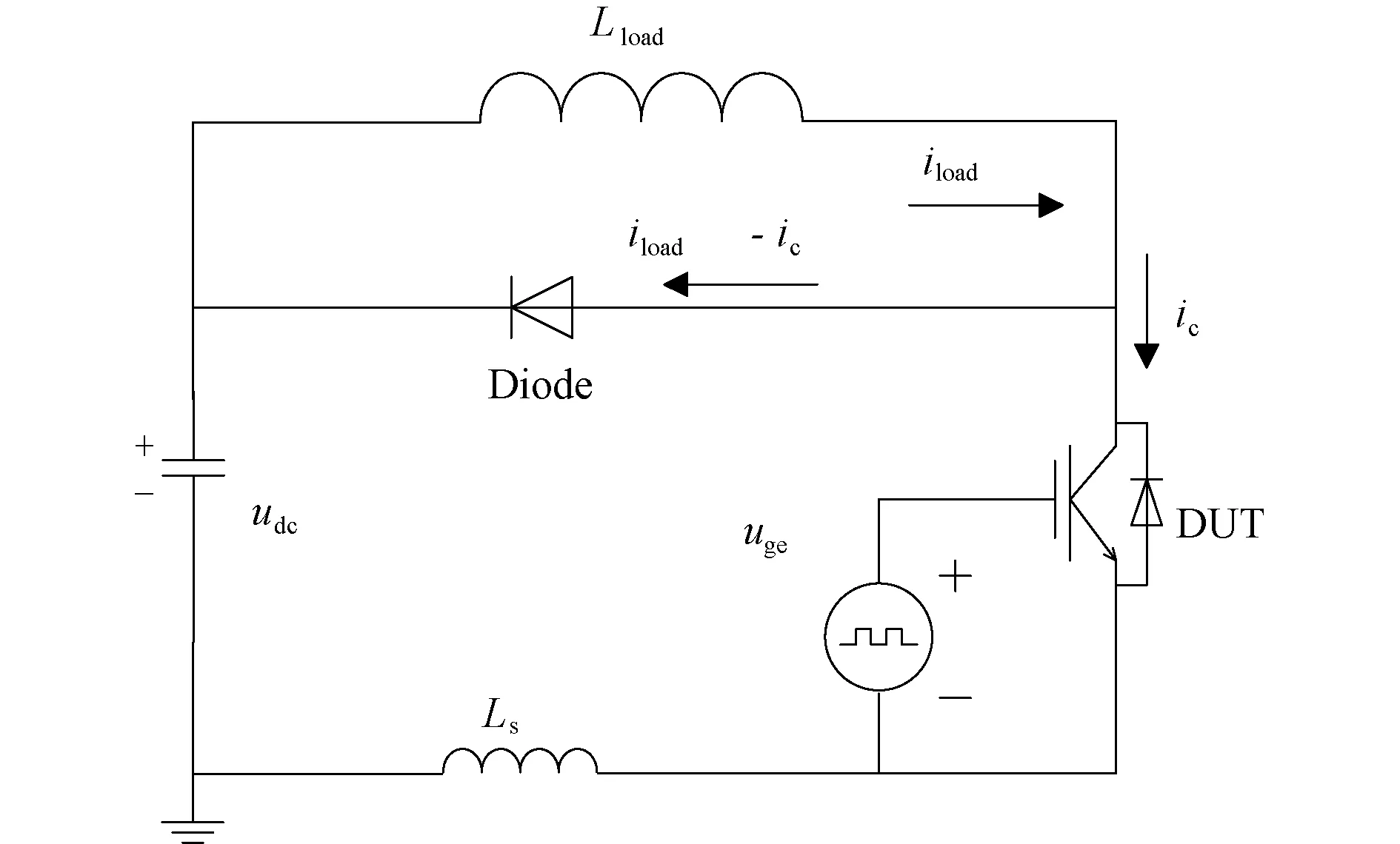
5 实验结果





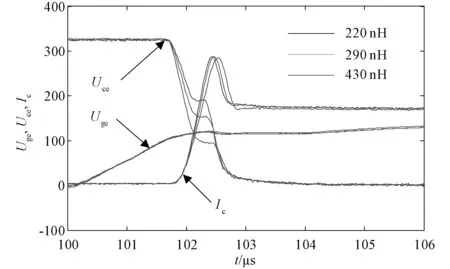
6 结 论
