数学解题教学应落实问题的本质
2017-04-21湖北省黄石市第六中学
☉湖北省黄石市第六中学 李 娟
数学解题教学应落实问题的本质
☉湖北省黄石市第六中学 李 娟
解题是高中数学学习中的一项重要内容,高考也通过解题来考查学生的综合能力及核心素养,进而选拔优质生源.解题教学是我们每位数学教师都面临的一项重要课题.解题教学是否到位,会直接影响到学生知识与经验的积累、思维能力的提升、解题能力的培养等等.那么应如何进行课堂解题教学?怎么才能实现解题教学效果最大化?笔者认为,抓住问题本质的教学是最有效的解题教学方式.下面以引例及其变式予以说明.
引例如图1所示,在棱长均为2的正三棱柱ABC-A1B1C1中,点M是侧棱AA1的中点,点P,Q分别是侧面BCC1B1和底面ABC内的动点,且A1P平行于平面BCM,PQ垂直于平面BCM,则点Q的轨迹长度为_________.
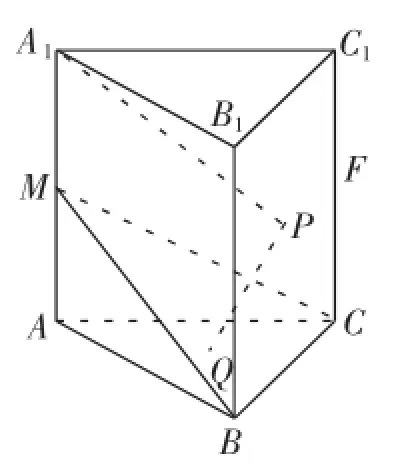
图1
此类动态立体几何问题活跃在近年各省市的高考试题中,“动态”的点、线、面元素,给静态的立体几何问题赋予了新的活力,题意更加新颖,也使得问题的形式更加灵活,有效地考查了学生的空间想象能力.那么此类动态问题的命题视角在哪里?在问题的解答中我们应采取什么样的策略?
“动中寻定”是处理动态几何问题的重要策略,这也是命题人的初衷.点P为平面BCC1B1内的动点,且A1P平行于平面BCM,所以A1P在与平面BCM平行的平面内,因此构造平面A1EF与平面BCM平行(如图2所示).由题意易知,E,F分别为棱BB1与CC1的中点.从而先确定点P在线段EF上.
接下来的问题是如何确定点Q的轨迹.先寻找特殊位置,取BC的中点N,连接MN,当PQ与MN相交时,设交点为T,此时点Q落在AN上,只要确定点Q在AN上的位置,即可确定点Q的轨迹.
从几何体中移出四边形A1ANP,如图3所示.
一、思路、方法要符合命题者的意图
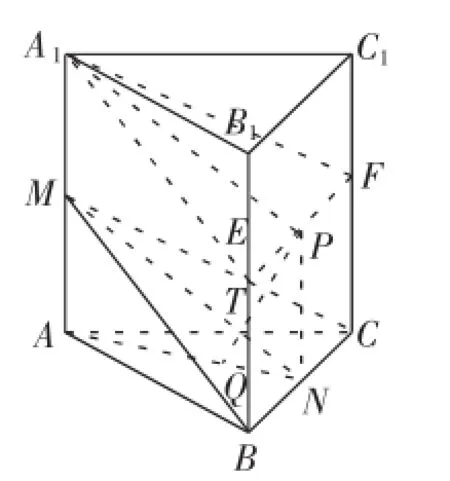
图2

图3
在△ABC中,过点Q作BC的平行线RS,分别交AB,AC于点R,S,即RS即为点Q的轨迹.由△ARS∽△ABC,得RS=
评析:寻找动点的特殊位置、空间问题平行化,进而利用平面几何知识求解,是处理本题的重要策略.
二、问题探究的过程中要形成解题经验
正确的解题方法与思路能够让学生形成解题经验,进而提升学生的解题能力、培养数学核心素养.
变式1如图4所示,在棱长为1的正方体ABCDA1B1C1D1中,点E和F分别是棱BC与CC1的中点,点P是侧面BCC1B1内的一点,若A1P∥平面AEF,则线段A1P长度的取值范围是().


图4
解析:如图5所示,取B1C1的中点M,取BB1的中点N,连接A1M,A1N,MN,由正方体的性质可得MN∥EF,A1M∥AE,所以平面A1MN∥平面AEF,即点P位于线段MN上.
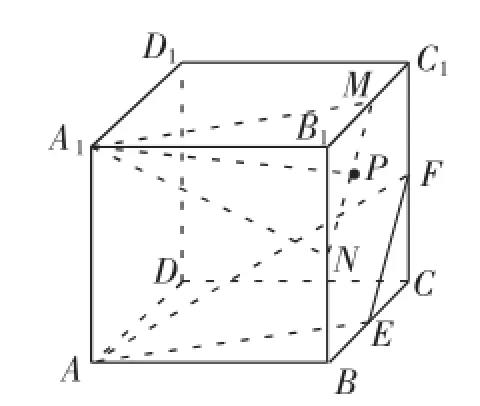
图5
在△A1MN中,有

所以当点P位于M,N时,A1P最大.

故正确选项为B.
评析:点P是侧面BCC1B1内的一动点点,但A1P∥平面AEF,所以A1P在与平面AEF平行的平面内,因此准确构造出平面A1MN是问题顺利求解的关键.
变式2在棱长为1的正方体ABCD-A1B1C1D1中,P1,P2分别为线段AB,BD1(不包括端点)上的动点,且线段P1P2∥平面A1ADD1,则四面体P1P2AB1的体积的最大值是().

解析:如图6所示,过点P2作P2O⊥底面于O,所以OP2∥DD1,且点O在线段BD上,连接OP1.
因为P1P2∥平面A1ADD1,所以平面P1P2O∥平面A1ADD1,
所以OP1∥平面A1ADD1,OP1∥AD.
又因为P1P2⊂平面ABD1,所以P1P2∥AD1,
所以P1P2⊥AB.
在Rt△ABD1中(如图7所示),易知AB=1,AD1=,BD1=,所以tanB=.设BP1=x,则P1P2=x,AP1= 1-x,所以S=·x(1-x).
△AP1P2
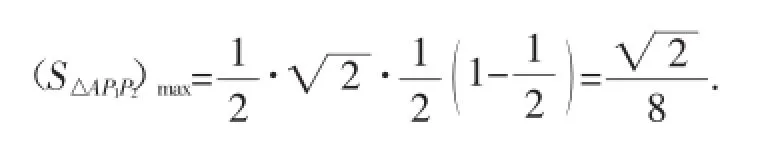
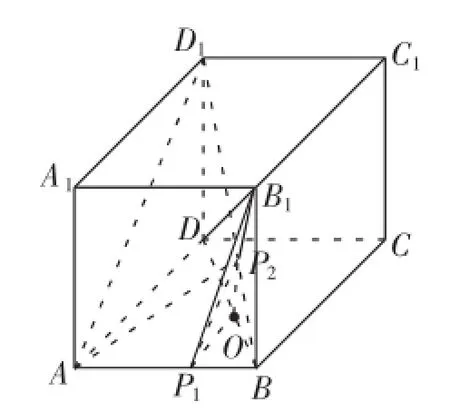
图6

图7

故正确选项为A.
评析:因为动线P1P2平行于平面A1ADD1,则P1P2在与平面A1ADD1平行的一面内,因此找到这个平面,使问题顺利求解.
通过上述深入本质的解题教学,学生很自然地将所学到的解题方法迁移到同种类型的问题中,从这个角度来讲,深入本质的解题教学至关重要.
三、解题后的反思要形成解答一类问题的通法
正确的解题方法,不仅能够解决该题,还能够将其迁移,解决同类型的试题,进而形成解决一类问题的一种通法.
(1)寻找不变量——以不变应万变.若动线与已知面平行,则动线在与已知平面平行的定面内.另外若定线与动线垂直,则动线在与定线垂直的定面内,找到这些定面即可使问题顺利求解.
(2)寻找直线段——化曲为直求最值.在处理与折线段有关的最值问题时,“化曲为直”是行之有效的策略.
(3)寻找特殊位置——化一般为特殊.几何体中的某种关系,若在一般情况下成立,则特殊情况中一定成立,因此可从特殊情况入手寻找问题的求解思路.
(4)寻找平面图形——空间问题平面化.空间几何体都是由平面图形构成的,在处理某些问题时,熟悉平面几何的相关性质,方可准确找到问题的切入点.
只要抓住上述几个要点,即可找迅速找到解答动态立体几何问题的求解思路.
满足了上述几点,对试题的讲解才能揭示问题的本质,使学生形成系统的方法,进而有效提升其分析问题与解决问题的能力,实现会一题而通一类.否则,只能是就题论题,停留在试题的表面,无法实现学生解题能力的有效提升.
