大道多至简，取势方明道——“析、译、拓”解题教学的实践与思考

☉山东省单县第一中学 卫小国

大道多至简，取势方明道
——“析、译、拓”解题教学的实践与思考

☉山东省单县第一中学 卫小国

基于能力立意的高考题，将对学生知识与技能、学科思维与素养等方面的考查，融入试题之中，落实于学生的解题过程，因此数学解题教学成为高中数学教学的重要组成部分.本文以一道高考题的教学实例，浅谈数学解题三步教学法的高效与实用.

基于波利亚“弄清题意、拟定计划、实施计划、回顾问题”的解题策略，教学需以典型的好问题促使学生“强化基础知识、提升基本技能、学习有效分析、总结解题规律”.结合解题教学实践的反思与总结，笔者特提出数学学科“析、译、拓”三步解题教学法.教学中应用此法，学生既能意识到数学解题“精准分析题意、高效转译思路、适度拓展延伸”的重要，又能实现思想方法、解题策略的迁移，达到解题的触类旁通.本文中笔者简录2016年高考山东卷解几试题的解题教学实践，并以其为例，详谈课堂实施的主体流程与各阶段设计意图.

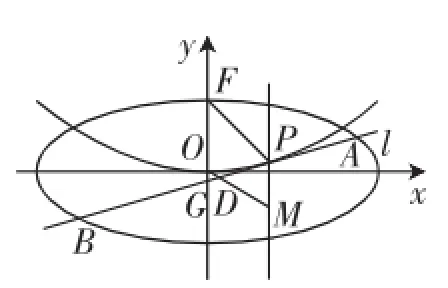
图1

（1）求椭圆C的方程.

（2）设P是E上的动点，且位于第一象限，E在点P处的切线l与C交于不同的两点A，B，线段AB的中点为D，直线OD与过点P且垂直于x轴的直线交于点M.

①求证：点M在定直线上；

②略.

其中第（1）问椭圆C的方程为x2+4y2=1，课堂教学仅集中研究第（2）问①部分；以期充分展示其指导解题教学的典型性.

一、精析解题思路，领悟命题意图

综合多个条件、多重关系的数学试题是考查学生问题分析与转化能力的最佳载体，要具有极高的教学价值.而突破问题“迷障”的最好手段，是着力培养学生准确审清题意和领会试题意图的能力.在平时的解题教学中，要顺利通过审题关，可借助典型问题引导学生分解题设条件、确定破题的方向、提炼问题的类型和选择解题的策略；与学生探讨解题思路的同步，教师无声渗透审题方法与解题策略的培养.

审题是题设有效信息的提取、隐含信息的深挖、关键信息的提炼，也是迅速解题的基础.审题要逐条审视题设条件，表征条件的应用或深挖与之有关联的知识（概念、性质、公式、结论等，甚至一些条件的必要条件），一个条件能向四周发散形成一簇.在思索如何使用这些条件时，条件就自然直接或间接地联系在一起，这样条件A（不一定是题目中出现的第一个条件）与条件B连接起来，条件B与条件C连接起来，…，如是，由突破口开始，用“无形”的线串起来，这就成为一种解题的思路.

课堂简录1析题

师：题设中，含有哪些几何要素与几何关系？

生1：题中主要包括的要素有：动点P，切线l，中点D，交点M等共四个；几何关系为：动点P是E上，l是E在点P处的切线，l交C所得线段AB的中点为D，直线OD与x=xP交于M.

师：很好！（适当鼓励，追问）所列的四个条件涉及到的相关知识有哪些？

生2：由中点D想到了联立方程组、韦达定理.

生3：交点M在直线上是线共点问题.点在直线上，可以涉及直线的点斜式或者交点直线系都可能.

生4：与切线l关联的有直线与圆锥曲线的位置关系，在对称轴为y轴的抛物线背景下，切线可以联想到导数的几何意义.

……

师：由此可见，从一个条件出发，获得的分结论有可能很多.如何将包含的信息组合，并以逻辑推理的形式条理成序，这就是解题思路的生成过程.因此，大家对题设条件的深挖，必为解题提供有效信息.

设计意图：问题中的条件是解题的逻辑始发点，结论是推理的目标；顺利搭建起点与目标间的桥梁是解题“通畅”的关键.分析问题的过程，需字斟句酌地分析条件，抽离出“隐藏”其中的数量关系与空间形式；再进行一系列的有序组合，形成清晰、条理、明确的解题思路.所以，教学中精析问题，厘清知识和思想方法，是建立新旧知识与经验间的有效联结.

师：下面结合初步的分析探究解题思路，以图示的形式展示思路过程，并简短解释你设计的想法.

生5：条件中最关键的条件是“点P”，它决定了另外的三个.思维流程如下（学生展示图1，简记解题策略一）：

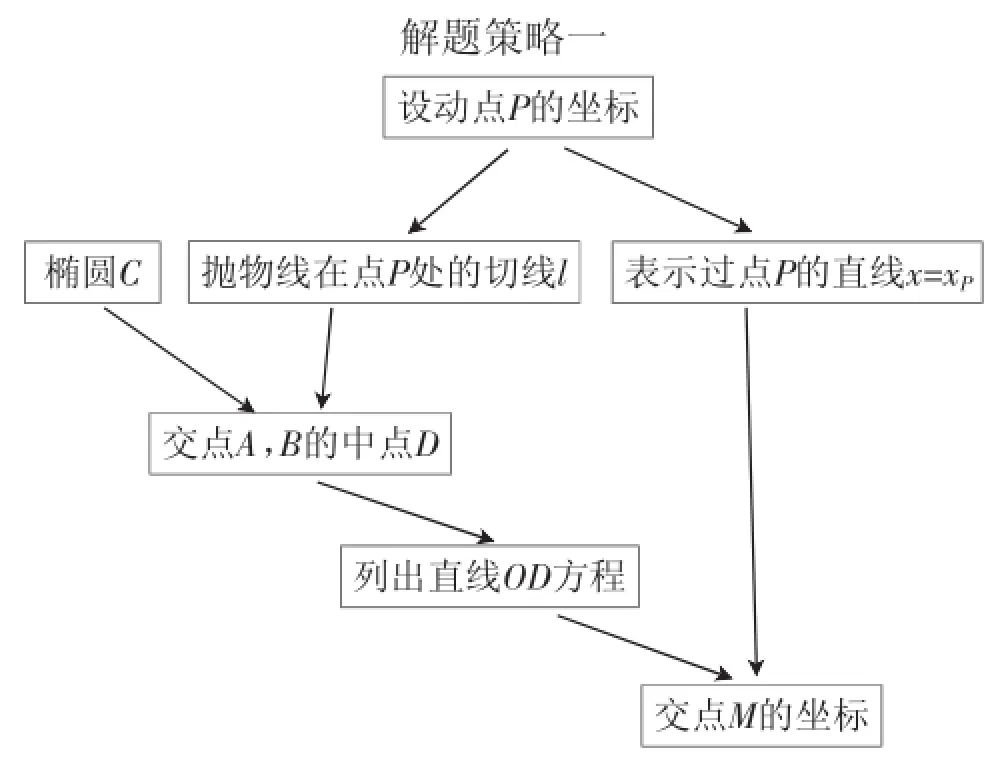
图1

预想只要设出点P的坐标，利用导数可求出切线l的方程；尔后与椭圆联立得到AB中点；最后通过直线OD与直线x=xP相交，算出点M的坐标.计算中主要还是常用的处理技巧，如“设而不求”与“整体代换”等.

师：思路很清晰，针对问题能“巧取节点，以少胜多”，稍后再探究详细的解答过程，哪位同学还有不同的解题思路吗？

生6：从结论出发，逆向寻求，主要过程如图2（简记解题策略二）：

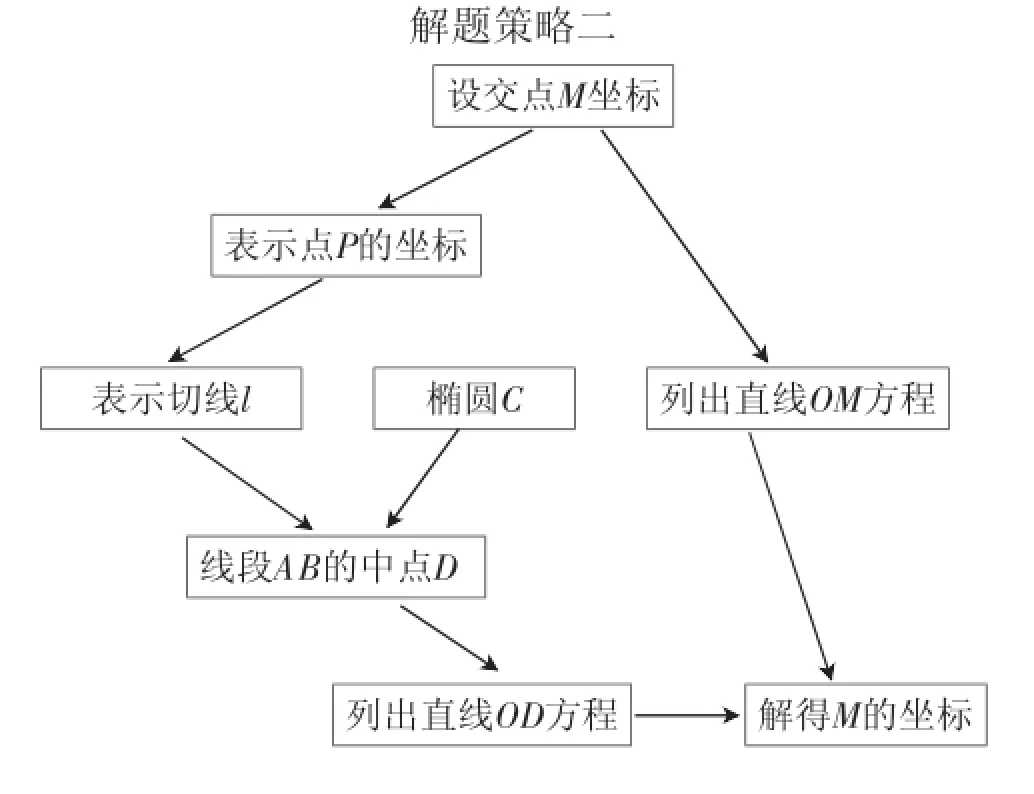
图2

设点M的坐标，就能表示出点P和直线OM；其中由P可列出切线l的方程，与椭圆C联立可得中点D，通过直线OD与直线PM的方程组，解得M的坐标.个人认为待定系数法、韦达定理、函数与方程思想的考查是重点，其中分析法是解决该类问题的好方法.

（众生有异动，意欲表达看法）

师（声调拉长）：嗯……

生7：这种解法是由结论出发寻求满足的条件；但是，运用于本题，预计计算量有点大.其中的原因是，点M是“设而待求”；需要通过“借点M表示点P，列出切线方程，联立方程组表示出中点D，根据直线OD与直线OM是同一直线，待定系数法确定点M的坐标”等一系列带字符的多重运算.

师：解析几何的字符运算能力是考查之一，也是难点，大家还是需要在平时训练中迎难而上，并学会在实施运算过程中遇到障碍而调整运算.本题采用的“执果索因，把握关键”的战术，是解决思维受阻的很好方式.若按生6的思路计算繁杂，既然如此，还有另辟蹊径的处理方法吗？

生8：观察到问题中，涉及原点与弦中点连线斜率及弦所在直线的斜率这两者，这是圆锥曲线“垂径定理”适用的典型背景；所以此题可选用点差法，大致的思路如图3（简记解题策略三）：

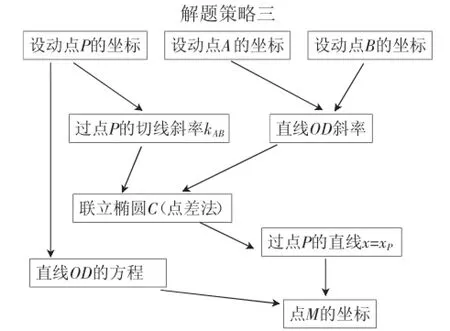
图3

分别设点P，A，B的坐标，如是可以由点P表示出直线x=xP与切线l的方程，由A，B代入椭圆方程获得方程组；利用点差法化简得直线OD斜率与A，B所在直线l的斜率之积.进而得直线OD的方程，直线x=xP与直线OD联立即得点M的坐标.这种方法充分说明，此题考查直线与圆锥曲线的位置关系、韦达定理等知识点，以及设而不求的运算处理和学生创新解题意识.

师：解题切入很巧妙！根据条件中的切线斜率与中间关键结论（直线OD斜率）的关系；于多个变量的纷繁关系中，将减元的策略通过“垂径定理”实现，真有一种“横刀立马”的气概！

设计意图：提供机会让学生深入理解题意，分析条件与结论的关系；以思维导图的形式直观表述出解题思路.一方面，导图提示学生知晓“如何设元”、明晰“有何关联”、确定“怎样联系”；另一方面，图表指引学生选用熟悉的解题策略与解题处理技巧，使得解题的方向明、操作清.这个过程，不仅浸润了解题策略的抉择，也自然成为解题的“导航仪”；把解题思路的设计与对命题意图的理解直观表述出来，让结论在解题前“在观念中存在着”.

简评：解题教学中的“析”，即是课堂中发挥教师的指导功能，并以问题导引学生展现思维过程；给学生时间以“读懂析透”题意，即学生弄清告诉的信息是什么、厘清考查什么思想方法［1］.正如涂荣豹所言“善于解题的人用一半的时间理解题意”.学生在课堂的时空中实践逐项解读条件、逐条转化已知、逐步关联串并，亲身感悟解题“快阅读、慢审题、精分析”的真谛.在突破审题关同时，学生交流获得解题切入方式，在“碰撞”中优化、抽象思维水平在“冲突”中提升.

二、转译导图信息，布局演算推理

前一步，是“谋篇”之始，是算法层面的分析，是与试题的“初步接触、浅层交流”；而后继则是“布局”之时，是推理与运算的主观呈现.若把以上的导图看成绘制“航道”，下面的转译则是破浪“航行”，是分析思路和解题策略的具体化.

课堂简录2译图

师：结合刚才几位同学的思路分析，请从图1和图3中自选一种，写出详细的解题过程.（教师巡视，掌握学情）

设计意图：解题教学中，以问题串“循序渐进”地导引学生结合前面的分析，进行解题的自我设计、统筹谋划，从文字叙述、代数翻译、演算推理等方面合理布局.学生的思维过程在课堂中有机会得以“暴露”，其中推理论证的严谨与创新、解题运算与调整技巧等解题细节能完整呈现.学生完善解题思路、老师点评解题过程，在师生的畅通交流中；学生的解题从“思”的层面，向“行”的层面过渡.

师：请生9、生10分别投影展示解法！

生9：（投影）

所以直线的斜率为m，

直线l方程为y=mx-

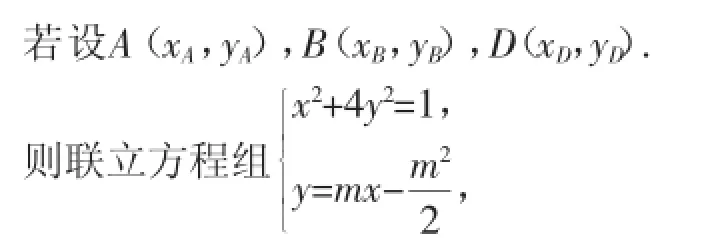
得（4m2+1）x2-4m3x+m4-1=0.

由两者相交于不同的两点A，B知，

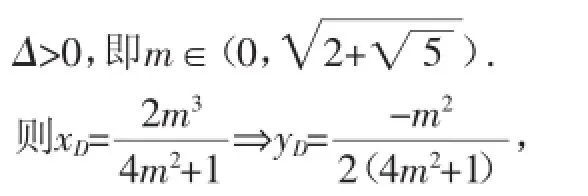
生10：（投影）

解：若设P（xP，）（xP＞0），又设A（xA，yA），B（xB，yB），D（xD，yD）.

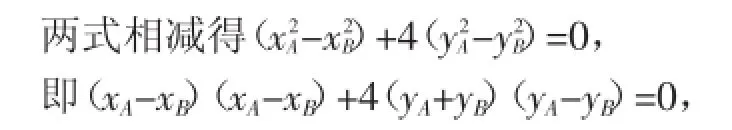
ODAB

另直线与抛物线相切时，由导数的几何意义，可得kAB=xP.

师：生10对策略三的“转译”，抓住题设条件的核心关联，利用圆锥曲线的点差法得到斜率间的关系式kODkAB=-.相对解法一，虽表面所设未知量较多；似“千军万马”，但巧借“垂径定理”，回避了“联立方程，韦达定理”，自然极大程度地降低运算量，解答简约.

师：上述两种解法虽切入不同、解答有异，但殊途同归，即运用参数法推证点M的运动轨迹在一条定直线上；两者都突出考查推理论证、运算求解等能力和转化化归的数学思想［2］.

另外大家要有心理准备，就是数学解题的字符繁多、变量繁杂；常常需要进行条件化归，常通过“消参”来简化.建立条件与结论之间的等式关系，是将复杂问题简单化的“必经之路”，其中结论是“上索下求”确定如何消参的关键.

设计意图：“一题多解”的对比中，是优化解题的实现的基本途径，学生的分析运算条件、探究运算方向、确定运算公式、选择运算程序是各有千秋的.之所以如此安排，一来通过学生的示范和老师点评，“润物无声”地促使全体学生自觉做到解题有条有理、清晰布局、严密推理；二来与学生共同探讨运算调整的时机，以便深化运算求解能力，从而达到运算简化、推理简洁.

三、拓展外延范围，探索内涵思想

解题教学中，基本的任务是确保学生掌握基础、学会方法，但引领学生注重试题背景、重视思维内涵，是学生“迁移应用、形成能力”的最佳途径.即以一题多解透彻分析问题很重要，但挖掘试题的内涵思想方法与拓展外延知识，则是解题教学的核心，使得解题教学的目标直指“研一题、会一类、通一片”.

（一）思想与背景的探索

简录3探源

师：波利亚所言“好问题类似于采蘑菇，采到一个后还应四处看看，也许还有更多”.就本题而言，其知识背景是什么？原题的四个条件与所证明的结论，是否可进行多种组合？

设计意图：圆锥曲线中的典型问题，常常是抽取了本质、隐藏了背景、呈现着表象，内在蕴含着特殊到一般的数学思想.解题的题源探究是弄清背景、探求本质、正本清源，是思维从内隐走向外显.因此，教学中可适当作一般性结论推广的猜想与论证，尔后条件与结论的可逆性分析与外延；特别是圆锥曲线间的拓展，通常会在“蘑菇四周发现蘑菇群”.

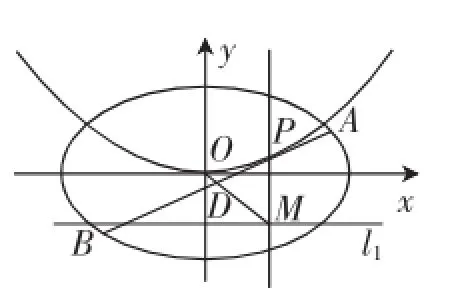
图2

师：下面请生12简单叙述一下.

生12：原题的推导方法和证明过程中，用字符替代即可，得到以下的解题过程：

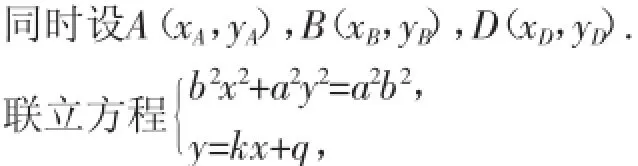
得（b2+a2k2）x2+2a2kqx+a2q2-a2b2=0.

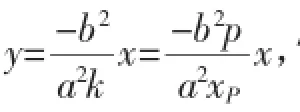
由此，直线OD方程为它与直线x=xP相交于M.

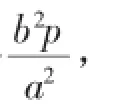
其纵坐标恒为y=-即有点M在定直线y=上.

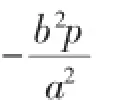
师：很好！生12的证明过程正是有特殊推广至一般，是归纳推理与综合法证明的综合运用，也是山东高考题的一般性推广，更揭示出该考题的知识本源.

生13：我认为一般的推广，还可以得到个更“漂亮”的结论.推理论证获得结论过程之时，代入切线的斜率才使得点M的纵坐标为定值，即点P处的切线l与点M在定直线y=-上是互相制约的.对一个命题从正反两个

角度进行探寻，发现生9的逆命题也成立.结论与证明过程展示如下：

设直线l的方程为y=kx+q，

解析：设点M

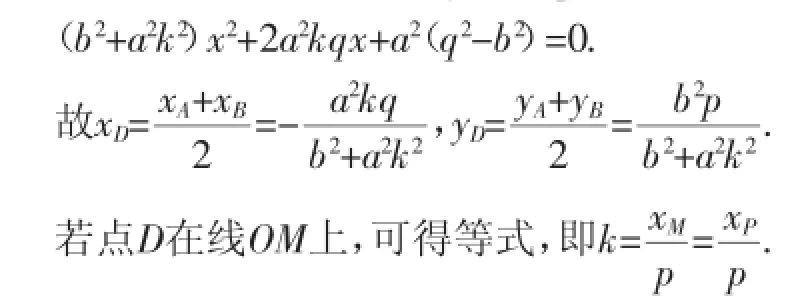
故直线l为E在点P处的切线.

师：能将以上的精彩推理，用一段话总结吗？

师：大家刚才精彩纷呈的问题分析和探究论证，完全可以将上命题归纳为一个定理了.事实上，该结论道出了高考试题的一个深刻的背景，也揭示了内在的奥秘，反映出“动中有定，变与不变”的本质特征.试题将以上定理所蕴含的规律，是利用特殊化思想，将试题其中的本质属性隐藏起来，这就为我们提供了深层思考的好素材和广泛的空间.

设计意图：解题教学中的挖本掘源，是算理的建模过程，也是思维的“蜕变”，多题归一，提炼方法，揭示思想，更是解决“一听似懂、一做就错”顽疾的高效措施.

（二）外延领域拓展

思维的高境界是思维发散性广、思维创造性强.解题教学的外延阶段，是可从特殊情形、简单问题入手，运用类比推理拓展至邻近领域，即数学的“大道至简”.

简录4拓展

师：圆锥曲线中的结论，常具有统一性，那么此定理是否可以进行延伸至其他圆锥曲线？请各组自选方向论证！

设计意图：利用圆锥曲线性质的相似特征，引导学生通过变式和拓展，在发现“蘑菇群”的同时也构建了一个命题网络.于学生而言，登高望远，收获的不仅仅是知识，更重要的是享受了成功的喜悦.在“源与流”的探寻中，思维水平和解题境界有了真真切切的提升.

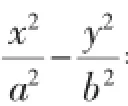
（投影）先探究充分性：

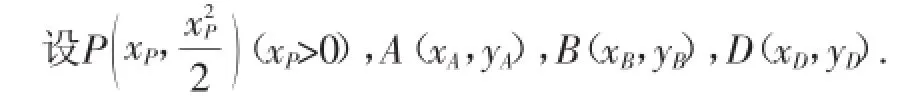
由题设知，直线AB与双曲线相交，则有

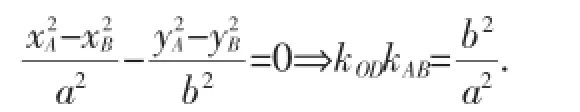
M由直线OD与PM相交而来，

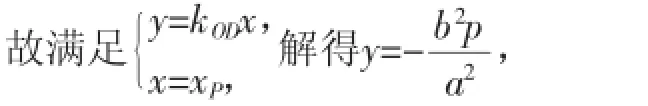
再探究必要性：

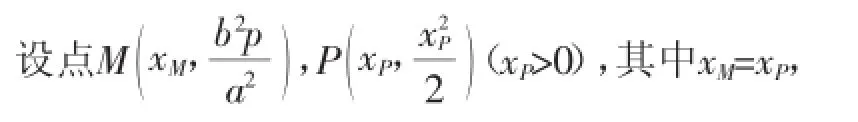
另可设其他点A（xA，yA），B（xB，yB），D（xD，yD）.

设直线l的方程为y=kx+m，

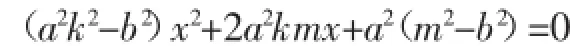
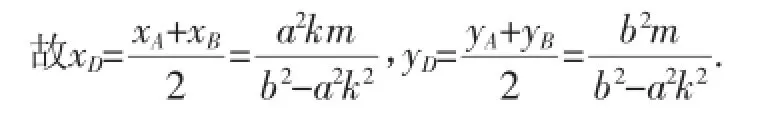
故直线l为E在点P处的切线.

师：推理过程很严密，而且获得结论的同时，也就实现了解题方法的迁移，原始问题的结论可以类比到双曲线.那么抛物线也有相似的结论吗？

组2：我们组探究的是这个方向，在抛物线中没有类似的结论！

师：那我们在抛物线这“滑过”（课前已知不能推广），还有其他需要补充的吗？

组3：我们用了一种特殊情况，也有收获：在平面直角坐标系xOy中，曲线C：x2+y2=m（m＞0），抛物线E：x2=2py（p＞0），设P是E上的动点，且位于第一象限，过E上点P处的直线l，若与C交于不同的两点A，B，线段AB的中点为D，且直线OD与过点P且垂直于x轴的直线交于点M，则直线l为E在点P处的切线的充要条件是点M在定直线y=-p上.证明只需要将椭圆特殊化，就可以轻易证明的.

师：太好了，大家联系一下这几点收获，能有统一的结论吗？

1（mn≠0），抛物线E：x2=2py（p＞0），设P是E上的动点，且位于第一象限，过E上点P处的直线l，若与C交于不同的两点A，B，线段AB的中点为D，且直线OD与过点P且垂直于x轴的直线交于点M，则点M在定直线上的充要条件是直线l为E在点P处的切线.

师：高考试题通常有一个“源”，而呈现的问题是千变万化的.我们需经历层层剖析，透过现象才能看到本质，得到上面的结论.对问题的细致分析是解题的基础，而构建出思路导图是解题策略的展现，解题过程是直观图示的代数化，问题的拓展与延伸是“看山不是山，看水不是水”式思想方法的迁移.

简评：在以上的探究过程中，引导着学生对问题深层次的思考，不断推动学生探究，萌生新的想法，对问题的理解更通透，由然而生解题中“会当凌绝顶，一览众山小”之感.

四、教学思考

罗增儒说：“数学学习中发生数学的地方都一无例外地充满着数学解题活动.”数学教学要“以解题为中心”，任何学习都要“以解题为中心”——有“问题”才需学习.解题过程就是学习新知、发展智力、提高能力的过程，当然也是“学会解题”的过程.如何达成学生的会解题？在解题教学中师生扮演好各自的角色；解决好“以如何发现和提出问题、如何获得数学对象、如何构建研究线索以及掌握解决问题的基本方法等为目标，通过解题逐步让学生学会认识和解决问题的基本方法”.

1.引导分析问题

解题教学是中学数学课堂教学的主旋律，但解题教学的课堂却异化了：解题教学演变为海量讲题、经验传授，结果学生“讲过练过不一定会，没讲没练的一定不会”；解题仅是题型训练、解法套用、试题记忆，最终学生“陷入题海而自拔无门”.其根本原因是在解题教学中，师生审题不清，更不谈“反刍”进而“提取”，建立不了新旧知识与经验的联系，忽视了问题的分析对思维培养的促进作用，

审题要“细”，要阅读每一个已知信息，进行慢推敲、抓细节.首先是读懂字面含义，列出题设中含哪些相关概念、定理、思想方法，有什么隐含信息；将题中的已知条件、潜在条件及要求解决的问题一一标出，做到边读题，边打腹稿，如此，自然分析出题目的要点.再则弄清数学含义，对数学概念准确理解——清楚它们的来龙去脉，内涵与外延，清楚与其他知识间的联系；对公式、性质、定理等要准确掌握——清楚其数学表达的使用前提，适用范围，功能等.而后识别出题目类型，即对问题提供信息及分析所得信息，进行有序的组合；表征为学生头脑中所熟悉的情景与问题类型.

审题过程中，教师要发挥自身的教学智慧，引领学生挖掘试题的信息，揣测命题的意图，将已有信息对比分析，找差别、找共性、找联系、找特点，有意识地训练学生的审题能力，唤醒大脑中有关联的知识，改善学习“固化”的“想当然”的习惯，能够清楚“审什么、怎么审”.

2.取势优化思路

“取势”是“顺势而为”，善教数学者，要能“谋势而动，因势利导”.思路探求的过程，就是条件和结论沟通的过程，也是经由条件进行一系列的推理与演算，探求结论的过程.解题教学中更应以有效的问题链强化学生“运算”“推理”“逻辑”“结构体系”；层层递进地优化解题思路，以展示学生自主思考逻辑思维“循序渐进”的过程.

解题教学中可以将学生对问题的分析这一思维活动过程，由隐性向显性的设计，可借助设可操作流程图或思维导图来直观展示思维的“框架”，再用文字具体表达出来.此过程的顺利与否，是基于学生对问题的条件和结论间的关联把握的程度决定的.教师的主导作用是导引学生找始点、理关系、定方法、选定理、译导图；学生结合自我对知识的理解和掌握情况，规范书写出方法简单、层次清晰、论证准确的解题过程.因师生和生生观察问题的角度的不同，从同一问题中可发现的规律也不尽相同；教师要预知学生的思维特征和学生知晓自身的思维水平，在师生的交流、生生的交流的冲突中碰撞出思考的火花.学生不断地自省自查和修正完善，从解题切入和运算技巧上全盘考虑；在课堂上生成自己的、正确的、优化的解题思路.

3.延拓方可明道

“明道”：明即明白、懂得，道即规律、原则.明道者，明白原则、掌握规律也.“数学是自然的，数学是清楚的”，对有价值的数学问题的解题过程进行回顾和解题方法的重新认识；把具体事例中得到的东西概括到全体中去，就是对透过现象看本质.具体问题中的信息是丰富的、多样的，教师要掌控主要研究方向和设计好的问题串：同样的方法是否可以运用于更一般性的命题？试题的背景是什么？命题可以推广吗？等等，环环相扣地让学生掌握如何观察具体事例，学会归纳、抽象、概括；以期培养学生“从经验中发现规律”的能力.

与学生一同追根溯源的同时，是“教师普度、学生悟道”，是让学生认识到试题有根，于浩瀚题海之中悟法方得是岸，用联系的哲学观看问题，多题归一，是对知识的引申与拓展，也是思想与方法的推广与延伸.

本文得到安徽太和高级教师韩长峰老师的指导和悉心帮助，在此深表感谢！

1.罗增儒.数学试题审什么、怎么审？［J］.中学数学教学参考（上旬），2012（5）.

2.韩长峰，卫小国.2016年高考数学山东卷理科第21题初探.［J］.数学通讯（上半月），2016（10）.

3.李红春，翁华木.活用解题理论打造高效课堂——基于“怎样解题表”理论指导下的一节习题课［J］.中学数学（上），2014（4）.