例析动态立体几何问题的处理策略

☉江苏省海安县立发中学 季小冬

例析动态立体几何问题的处理策略

☉江苏省海安县立发中学 季小冬

动态立体几何中的最值问题，是学生学习的难点，也是高考命题及模拟考试命题的热点.最值问题的求解，通常有两种类型：

1.构造目标函数，将问题转化为函数最值问题，再利用配方法、均值不等式、三角换元、导数方法等求解.

2.通过准确认识题目所给图形中点、线、面的位置关系，明确取得最值的条件，利用转化与化归思想结合平面几何图形的相关性质求最值.

本文针对第2种类型举例说明.

题目（2016年北京高三期末理）在空间直角坐标系O-xyz中，正四面体P-ABC的顶点A，B分别在x轴，y轴上移动.若该正四面体的棱长是2，则点O，P之间距离的取值范围是（）.

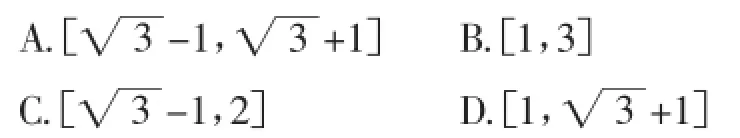
本题以特殊几何体——正四面体为背景，虽然只是一道选择题，但综合程度较高，能有效考查考生灵活运用所学知识解决问题的能力.此类问题因其动态、可变性，有助于学生空间想象能力及综合能力的培养.解题训练中要多方着力、合理转化、准确构造，找到最值取得的条件.

下面通过对此题的解答，探索解决动态立体几何的基本策略.

一、准确认识图形关系

正四面体是最基本的立体几何图形之一，若在平面中直观作出正四面体的图形，其几何性质不易体现出来.因此我们常借助于正方体，即把正四面体还原到正方体中，如图1.

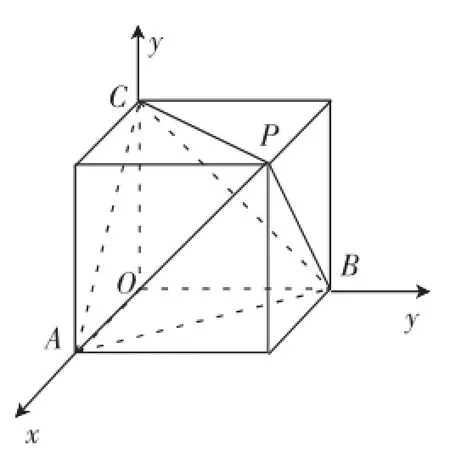
图1

借助于图1我们可清楚地认别题目中的几何图形的本质.

除此之外，在平行、垂直关系判定问题中，准确构造特殊的几何体，可快速解题，如：

变式1已知直线l，m，平面α，β，下列命题正确的是（）.

A.l∥β，l⊂α⇒α∥β

B.l∥β，m∥β，l⊂α，m⊂α⇒α∥β

C.l∥m，l⊂α，m⊂β⇒α∥β

D.l∥β，m∥β，l⊂α，m⊂α，l∩m=M⇒α∥β

解析：如图2所示，构造长方体ABCD-A1B1C1D1，在该长方体中AB∥CD，则AB∥平面DCC1D1，AB⊂平面ABCD，但是平面ABCD与平面DCC1D1不平行，所以选项A错误.

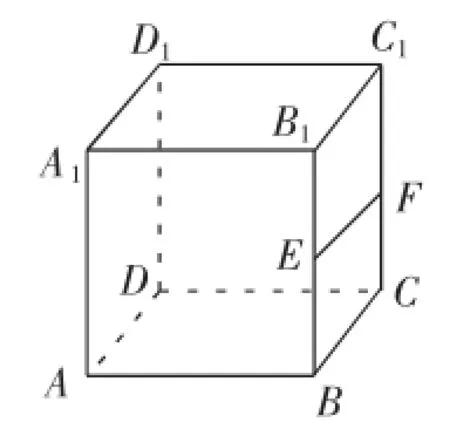
图2

取BB1的中点E，CC1的中点F，则可证EF∥平面ABCD，B1C1∥平面ABCD.EF⊂平面BCC1B1，B1C1⊂平面BCC1B1，但是平面ABCD与平面BCC1B1不平行，所以选项B错误.

由长方体的性质可证得AD∥B1C1，AD⊂平面ABCD，B1C1⊂平面BCC1B1，又平面ABCD与平面BCC1B1不平行，所以选项C错误.

很明显，选项D表述的是面面平行的判定定理，所以D正确.

故正确选项为D.

二、由特殊入手，空间化平面

将A、B置于正方体的两个顶点处，即先将点A、B固定，建立空间直角坐标系，随着点P的移动，|OP|随之变化.

空间问题平面化，是处理立体几何问题常用策略.由前面分析可知，点P的运动过程，即等边三角形PAB的变动，当点P运动到平面OAB内时，有如图3、4两种情况.

如图3所示，因为OA=OB，且三角形PAB为等边三角形，故OP垂直平分AB.设OP交AB于点M，易求得OM=1，PM=，所以|OP|=1+

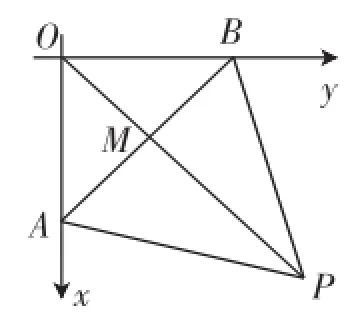
图3

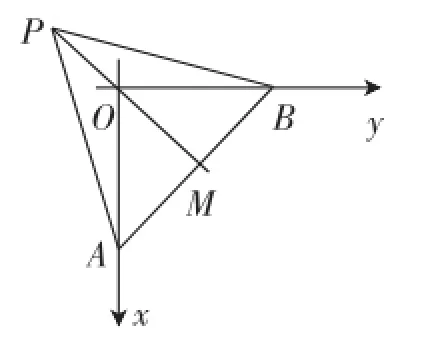
图4

由图4所示，因为OA=OB，且三角形PAB为等边三角形，连接PO并延长，交AB于点M，易知PM垂直平分AB，又PM=，OM=1，所以|OP|=-1.

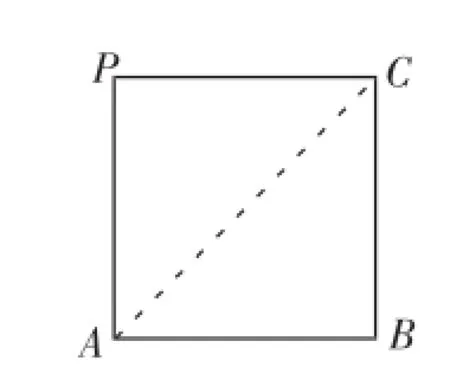
图5

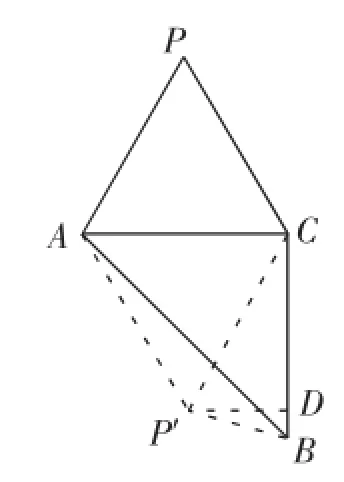
图6

在△PAB中，由余弦定理可得

PB2=PA2+AB2-2PA·ABcos∠PAB

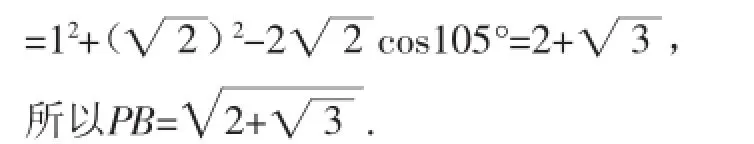
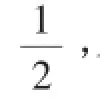
三、探究一般情况，比较见真知

通过以上的探究，其实我们已经得出了正确选项，那么接下来的问题是-1与+1是否就是最小值和最大值呢？

接下来我们再对一般情况进行探究，即当顶点A，B分别在x，y轴上移动时，O、P两点间距离的变化情况.

当点A，B在x，y轴上移动时，

（1）如图7所示，由三角形性质：两边之和大于第三边可知，|OP|≤+1；

（2）如图8所示，由三角形性质：两边之差小于第三边可知，|OP|≥-1.

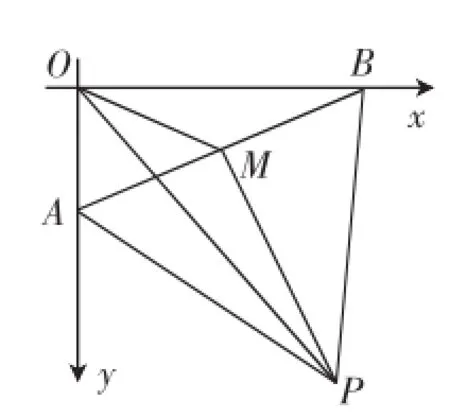
图7

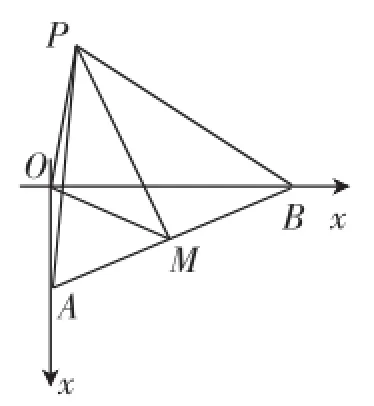
图8

综上，正确选项为A.

变式3如图9，空间直角坐标系O-xyz中，正三角形ABC的顶点A，B分别在平面xOy和z轴上移动.若AB=2，则点C到原点O的最远距离为（）.

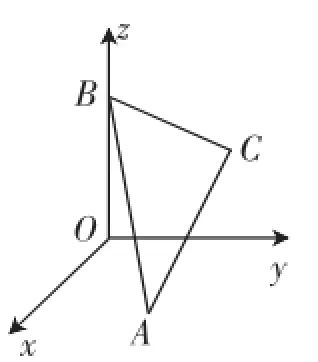
图9

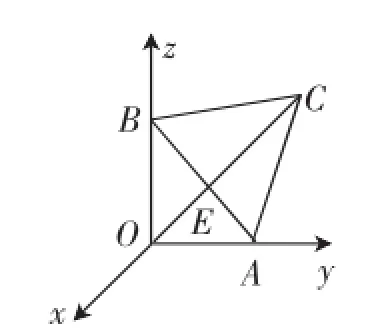
图10

解析：如图10，连接OA，取AB的中点E，连接OE，CE.因为Rt△AOB中，斜边AB=2，所以OE=1AB=1.又因为2正三角形ABC的边长为2，所以CE=AB=

观察图形知，当A，B分别在面xOy和z轴上移动时，可得当O、E、C三点共线时，C到原点O的距离最远，且最远距离等于+1.

故正确选项为C.

数学因运动、变化而精彩纷呈.动态问题的引入使立体几何的命题更加丰富多彩，以动态几何问题为基架而精心设计的考题题目灵活多变，动中有静、动静结合，能够在运动变化中发展学生空间想象能力和综合分析能力.