通用解法:数学解题教学的核心关注点
——以一道例题的教学为例
2017-04-21江苏海门市实验初级中学徐标
☉江苏海门市实验初级中学 徐标
通用解法:数学解题教学的核心关注点
——以一道例题的教学为例
☉江苏海门市实验初级中学 徐标
数学问题的解决方法很多,为了给学生多样化的解题路径,我们常会将“一题多解”问题作为数学教学的重要内容.然而,解法的拓展还是要适度的,我们更多地应将教学的重心放在一些通用方法上,因为,这些方法才是学生最容易接受,在今后的问题解决中最容易被应用的方法.在教学中,我们应找寻出这些方法,并将其呈现给学生,让他们在对比辨析中,实现解法的优选,从而获取问题解决的典型方法和常用套路.基于此,课前,教师应充分准备,对解题方法从多角度分析,找出与学生认知匹配的典型解法;课上,应认真观察、细致分析,努力发现学生给出的众多解法中与预设相符的通用方法,适时将其在全班展示、共享.现呈现“二次函数”复习课一道例题的教学历程,并谈一些个人的思考,希望能给你带来启示.
一、例题简析及其教学历程
1.例题及其简析.
在平面直角坐标系中,一个二次函数的图像经过A(1,0)、B(3,0)两点.设这个二次函数的顶点为D,与y轴交于点C,它的对称轴与x轴交于点E,连接AC、DE和DB,当△AOC与△DEB相似时,求这个二次函数的表达式.
简析:本题改编自陕西的一道中考题,为了突出对待定系数法、相似三角形等核心知识的考查,编题时,删去了原题第(1)题“写出这个二次函数的对称轴”.解答本题,可以根据A、B两点的特点,先用“交点式”设出函数的解析式,再利用二次函数图像的对称性将顶点D与E的坐标表示出来,从而将两个三角形的边长表示出来,最后,根据相似三角形的性质进行充分的分类讨论,求出解析式中的未知系数即可.
2.教学过程简录.
学生自主解答,10分钟后开始全班交流.
师:下面我们一起来交流一下这道例题的求解过程.
生1:根据题意,我设这个二次函数的解析式为y=a(x-1)(x-3),即y=ax2-4ax+3a.
师:你是怎样想到这样设的?
生2:这里给出的两个点A(1,0)、B(3,0),正好是抛物线与x轴的两个交点,所以,我自然而然就想到交点式y=a(x-x1)(x-x2)了,这是我们求二次函数解析式的常用方法.
师:是的,用待定系数法求二次函数的解析式,要结合所给点的特点从一般式、顶点式、交点式中“优选”.对于这道题,从交点式入手,回避了烦琐的解方程组,节省了很多解题时间.接下来该怎么做呢?
生3:利用得到的y=ax2-4ax+3a,可以分别求出点C、D和E的坐标,即C(0,3a)、E(2,0)、D(2,-a).
师:求出这些点有什么用呢?
生4:可以将△AOC与△DEB的直角边分别表示出来.
师:你是怎么发现这里的直角三角形的?
生5:作图,我将求出的这些点大致在图1中标出(C点也可以在y轴的负半轴上).显然,∠AOC=∠DEB=90°.这样,我就找到了这对相似三角形的一对对应角,确定了一对对应顶点.
师:这一步叫什么?生(齐):找对应顶点.
师:很好!找到了一对对应顶点,下面该做什么了?
生6:用对应边分类,共分两类,AO与BE为对应边;AO与DE为对应边.根据“抓关系式求解”,由两种情况可以分别列出,从而求出a的值.
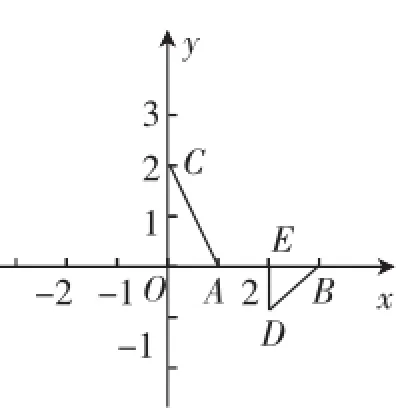
图1
师:你说得真好!“找对应顶点,用对应边分类,抓关系式求解”,是我们解决函数视角下的相似三角形问题的通用方法,这一方法在解答本题时,得到了很好的应用.下面我们一起来看一下这道题的完整解题过程.
(教师投影展示一名学生给出的通用解法,并让学生对照调整)
二、教学过程简析
本题涉及的待定系数法和相似三角形都是初中数学的核心知识,这道例题的教学一方面要回顾这两个知识,同时还要培养学生应用与这两个知识相关的典型解法的意识.案例中,学生首先交流了求二次函数解析式的历程,将“优选”的解法直接与全班同学作了分享;接下来,交流了用作图将数向形转化的过程,找出了数与形的结合点;最后,紧扣问题解决过程,对相似三角形的“找对应顶点,用对应边分类,抓关系式求解”的典型解法进行了再梳理.语言的陈述和书面的展示,学生个体的展示实现了解法的共享,所有学生获得典型解法的同时,还都能感受到这些方法在问题解决中的巨大价值.
三、几点思考
1.例题教学应突出通解、通法教学.
通解、通法是解决数学问题的一般方法,在学生解题中是应用得最多的方法.因此,例题教学时,我们应突出通解、通法的教学,力求让学生掌握一类问题解答的一般套路或常用方法.本文中,教师所设计的例题,指向的正是用待定系数法求二次函数的解析式和基于函数图像之上的相似三角形的求解常用套路——“找对应顶点,用对应边分类,抓关系式求解”.显然,教师对例题的教学处置很好地将例题的教学核心凸显了出来.仅就解法交流而言,教师选取了本题最为常用的解法进行交流,弱化了“边缘”解法,将例题需要交流的核心内容推到了学生认知活动的最前沿,其教学成效还是比较显著的.
2.例题教学应重视思维过程展示.
例题教学除了解题方法的教学,还要关注学生思维过程的分享.教师在教学过程中,应该努力找寻学生中出现的具有示范意义的思路分析历程,将这些具有代表性的思维历程通过全班交流,实现共享,以全面提升学生分析问题和解决问题的能力.我想,本文案例中的老师可能正是基于这样的思考才通过步步紧逼的追问,让学生将自己获得通解、通法的思维过程完整展示在全班同学面前,这样的交流,不纠结于具体的解题步骤和解题结果,而是由学生陈述带有明显个性特征的分析问题和解决问题的思路获得过程.这种来自于学生的思路交流,对于处于同一情境中的学生而言,是可以学习、可以借鉴,甚至是可以复制的.我想,在此过程中,每一名学生都能从中收获到自己认同的东西,不只是知识,经验可能更为重要.
3.例题教学应强化数学思想交流.
例题的通解、通法教学,除了上面所述的常用方法和典型思维过程,还应包括基本数学思想的教学.在数学教学中,数学思想一直是最为重要的教学内容.基于数学思想的可应用性和可生长性,它理应成为例题教学的“常客”,教师在教学时必须予以重点关注.我们还是回到本文中的例题上来,纯文本的陈述并不代表不需要图形,在解题时,学生5作出了图1,而且用图1很好地解决了问题,这就是数形结合的绝佳体现,其富有成效的陈述给全班学生作出了很好的示范,也让数形结合思想再次深入到学生的心中;学生6能给出“两种情形下的方程,正是其对分类讨论思想的深刻认知与反复应用的自然生成,他的展示既是自身对分类讨论思想的再度强化,同时还加深了其他学生的认知……正是教师对数学思想的穷追不舍,一个个潜在的数学工具才逐步显山露水摆放在学生眼前.这样的成效,自然触动着每一名学生的“解题神经”,思想的内化应用是迟早的事.
