解题研究再深入:以一道习题网络研讨为例
2017-04-21重庆市涪陵第十四中学校贺清伦
☉重庆市涪陵第十四中学校 贺清伦
解题研究再深入:以一道习题网络研讨为例
☉重庆市涪陵第十四中学校 贺清伦
网络研题是当前一个热点教研现象,突出表现在一些主题QQ群、微信群里,由于网络平台打破了时空的限制,且交流上没有地位、名气、权威的限制,较能畅所欲言,常常也能见到不少精彩的论述.本文记录一道习题在网络上的深入研讨,并给出跟进反思,供分享.
一、一道几何习题的解法突破
(这是QQ群里某教师提出的一道习题)
题1:请用三角板、圆规或量角器等工具,画∠POQ= 60°,在边OP上截取OA=20mm,在边OQ上截取OB= 30mm,连接AB,画∠AOB的平分线交AB于点C,并求出AC∶OC的值.
网络研讨简记:很快就有人给出该题的思路贯通,限于篇幅不展示原题的解答过程,我们把问题重新表述为题2,当然,不改变原题的结构与求解目标.
题2:如图1,BD为等边三角形
ABC的角平分线,点P为边BC上一
点,且BP=2CP,连接AP交BD于Q,求
PQ∶BQ的值.
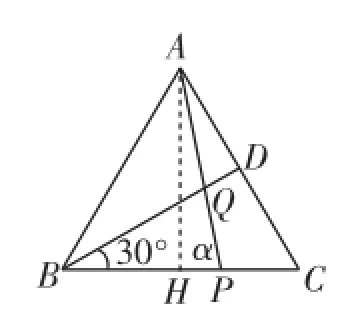
图1
在△ABP中,由角平分线性质,可得PQ∶AQ=2∶3,于是
在△BPQ中,利用正弦定理,BQ∶sinα=PQ∶sin30°,代入计算,得出PQ∶BQ的值为
思路2:如图2,再补一个等边三角形ACM,则有菱形ABCM,根据相似性质,结合上一问中求出的AP长,容易求出BQ∶QM=BP∶AM=2∶3,从而也可求出BQ的长(避开使用正弦定理).
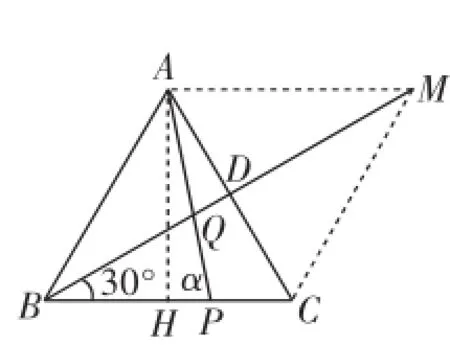
图2
思路3:(九年级学生提供)以B为坐标原点构造平面直角坐标系,解出直线AP、BP的方程,再联立求出交点Q的坐标,然后利用两点间距离公式求出BQ、PQ的长.
典型错误解法:研讨过程中,也有人指出问题就是求图1中等腰三角形BPQ的底边与腰之比.这是一种典型错误,该错漏原因在于想当然地认为△BPQ是等腰三角形,我们可以利用几何画板构造图3看清上述观点的错误所在.
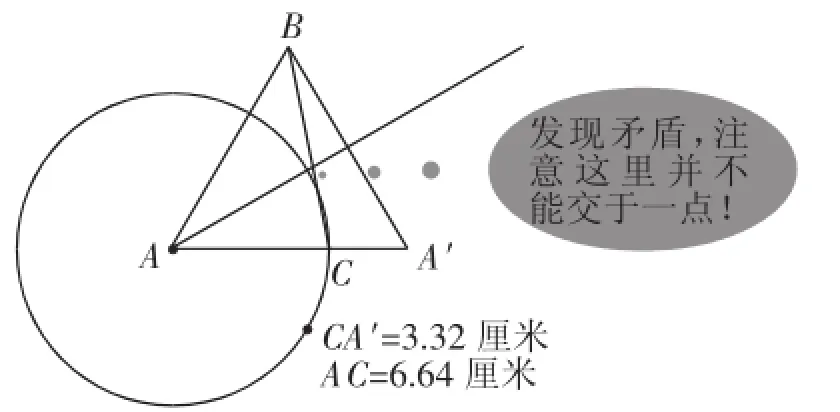
图3
二、变式改编后精彩解法
题3:(题1的变式改编)如图4,△ABC中,∠ABC=60°,BD是角平分线,BC=4,AB=6.求sin∠BDC的值.
思路1:如图5,构造∠BDE=30°,作DF⊥BC于F.依次求出CD、DF、CF、EF、DE、BE、BD的长,最后利用正弦定理带来的面积公式得出等量关系获得突破.
图4
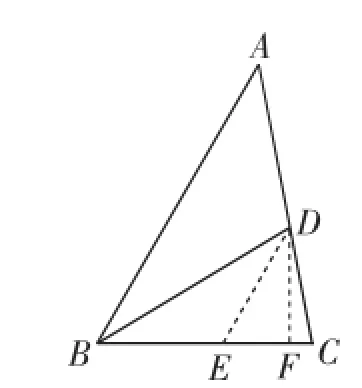
图5
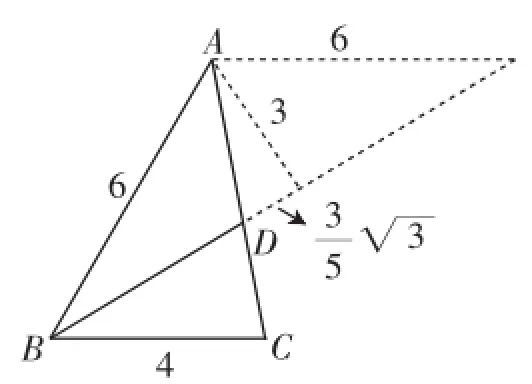
图6
思路2:这是一个老师构造的图形(如图6),并示意了相关求解数据,一目了然.
思路3:如图7,将原△ABC补成等边三角形ABE,并作CG⊥BF于G,延长BD交AE于F点,进而可确认F为AE的中点,容易根据相似三角形求出DF的长,从而获得思路贯通.
后记:笔者将该题作为家庭作业,布置给所教班级学生练习之后,再将上述变式与系列过程进行详细讲评,不少学生课后还以数学写作的方式整理该题的不同解题思路与变式.
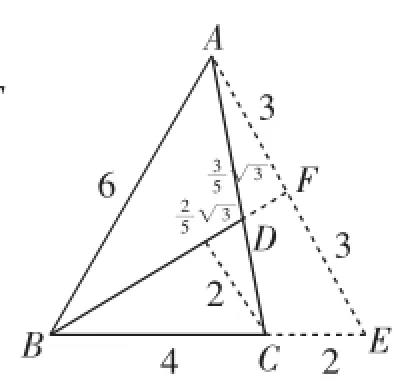
图7
三、关于解题研究的相关思考
1.解题研究要尝试多样化解题路径,在“善于比较”中走向“多解归一”.
教师的解题研究不同于数学家或数学竞赛型选手的研题方式,在较快的思路下贯通难题,就继续下一问题,我们需要追求服务教学,让更多的后进学生、理解有困难的学生能跟进理解.这就需要我们在解题研究时对一道难题的思路不能满足于单一的、狭窄的解题路径,而要设法探求出多样化的解题路径.在获得一道题的多种解法之后,需要思考不同方法之间的关联,比如上文中图2与图6所对应的思路属于同一类;图1与图7所对应的思路也相对接近.当我们对问题的不同思路有了深入比对之后,才能居高临下地看待课堂上学生出现的不同思路,并作出即时而精准的评价或引导.
2.解题研究不能满足于就题论题,应在“洞察结构”之后“变式改编”.
常常见到不少解题爱好者解完一题,也能从不同角度贯通思路,追求一题多解甚至多解归一(这在不少期刊上的一些解题研究的文献中较为多见),然而这类研究还有深入下去的方向,这就是在洞察问题的深层结构之后,可以开展对问题的变式改编,在不破坏问题原来结构、解题目标的前提下,积极开展变式研究,这既是我国数学“双基”教学的特色,也有利于命题基本功、教学基本功的自主提升.比如上文中的题1到题2、题3,都可看成是这一方向的努力与尝试.事实上,我们见到很多优秀的中考试题,多数都是由之前大家很熟悉的某一类经典问题通过恰当的改编,包括改变问题呈现方式,改编设问角度,设计出来的.这种基于“多元表征”的变式研究是值得很多同行积极实践的,根据笔者的教学研究、命题研究的经验,能否在洞察问题结构的基础上进行恰当的改编设计,常常是一份试卷质量高低的重要指标,或者是一份教案中例题、习题选编的重要表征.
3.解题研究后注意素材归类搜集,并研发适合学生的专题学案.
作为必要素材收集与归类整理,我们在研究一些有价值问题之后要及时进行收集与归类整理,目前网络研讨之后不少有心的同行利用自媒体如微信、博客、QQ空间等平台坚持整理发布一些系列思考,并引发不少传播,是值得我们学习的.此外,我们还可把这些优秀的素材进行适当整理,研发适合学生的专题学案或微课教案.作为本文的最后,我们也将上文中的这道习题的研究资料整理成一份微课学案,抛砖引玉,供分享.
四、微课学案设计
设计教学时间20分钟.
教学环节(一)从等边三角形出发.
引例问题:如图8,BD为等边三角形ABC的角平分线,点P为边BC上一点,且BP=2CP,连接AP交BD于Q.
(1)设CP=2,求AD的长;
(2)设CD=3,求△ACP的面积;
(3)求tan∠APB的值;
(4)求PQ∶AQ的值.
教学环节(二)例题讲评
例题:(题1的变式改编)如图9,△ABC中,∠ABC=60°,BD是角平分线,BC=4,AB=6.
(1)求CD的长;
(2)求△ABC的面积;
(3)求△BCD中CD边上高的长;(4)求sin∠BDC的值.
教学环节(三)变式反馈.
变式题∶如图9,△ABC中,∠ABC=60°,BD是角平分线,BC=2,AB=3.
(1)求AD的长;
(2)求点A到BC边的距离;
(3)求BD的长;
(4)以点B为坐标原点、BC所在直线为x轴,构造平面直角坐标系xBy,求D点的坐标.
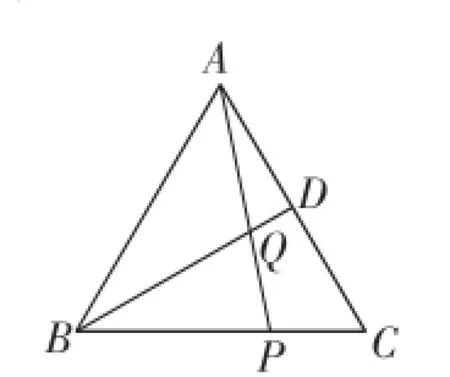
图8

图9
1.鲍建生,顾冷沅,等.变式教学研究[J].数学教学,2003(1、2、3).
2.朱金祥,刘东升.数学教学中例题变式的策略——基于教学追问的视角[J].教育研究与评论(中学教育教学版),2016(09).
3.郑毓信.善于优化[J].人民教育,2008(20).
4.郑毓信.多元表征与概念教学[J].小学数学教育,2011(10).
