聚焦微专题:中考二轮复习的实践与思考
——以一组“关联试题”复习为例
2017-04-21江苏苏州市吴江区松陵第一中学沈丽婧
☉江苏苏州市吴江区松陵第一中学 沈丽婧
聚焦微专题:中考二轮复习的实践与思考
——以一组“关联试题”复习为例
☉江苏苏州市吴江区松陵第一中学 沈丽婧
中考二轮复习期间,大量的复习资料、专题复习、模考试题需要讲评,常常在讲评之后发现不少看似形式差异较大的综合题,在解题思想、结构上却有一定的关联或相似之处.本文结合新近讲评过的一些习题作一些例析和跟进思考,供研讨.
一、关联试题思路简述与结构反思
(1)求k的值.
(2)如图2,将∠MON绕点O旋转,射线OM始终在第一象限,交l1于点C,射线ON交l2于点D,连接CD交y轴于点Q,在旋转的过程中,∠OCD的大小是否发生变化?若不变化,求出tan∠OCD的值;若变化,请说明理由.
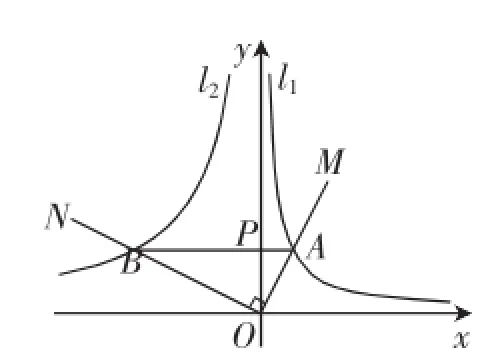
图1
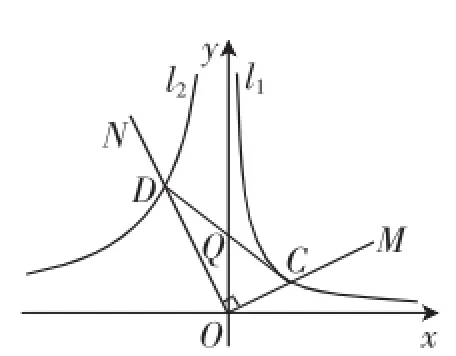
图2
思路简述:(1)限于篇幅不给出过程,k=-8.
(2)首先猜想∠OCD的大小不变.可以构造相似三角形来证明这一结论.如图3,过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F.
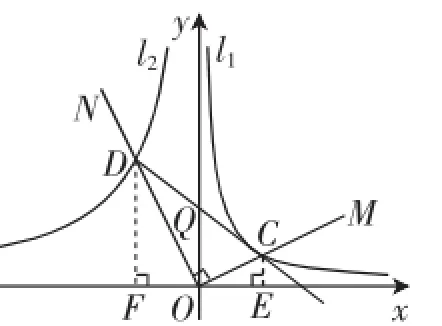
图3
结构反思:第(2)问的难点在于构造出△DFO∽△OEC,利用这组相似三角形的两条直角边对应成比例来贯通思路,而它们的直角边恰与直线与“双曲线”的两个交点的坐标有关!
题2:(2013年江苏南通中考,第28题)如图4,直线y= kx+b(b>0)与抛物线相交于A(x1,y1)、B(x2,y2)两点,与x轴的正半轴相交于点D,与y轴相交于点C.设△OCD的面积为S,且kS+32=0.
(1)求b的值;
(2)求证点(y1,y2)在反比例函数的图像上;
(3)求证x1·OB+y2·OA=0.
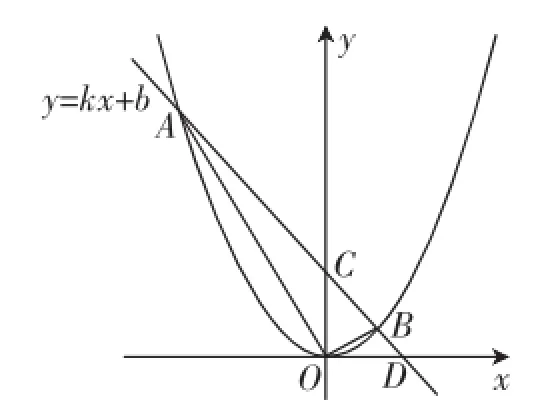
图4
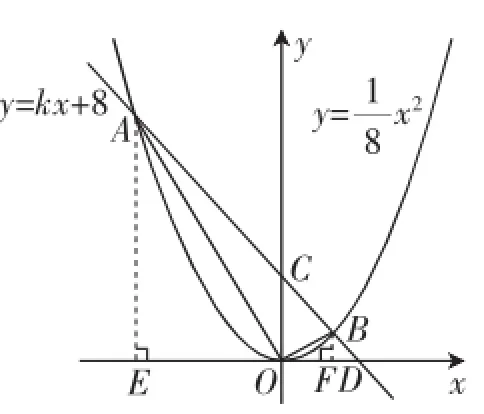
图5
思路简述:(1)限于篇幅,直接给出b=8.
则点(y1,y2)在反比例函数的图像上.
(3)如图5,分别过点A和点B作AE⊥x轴,BF⊥x轴,垂足分别为E、F,则OE=-x1,AE=y1,OF=x2,BF=y2.由(2)得y1y2=-x1x2,则又∠AEO=∠OFB=90°,则△AEO∽△OFB.则以-x1·OB= y2·OA,即x1·OB+y2·OA=0.
结构反思:如图4,直线y=kx+b(b>0)与抛物线y=ax2相交于A(x1,y1)、B(x2,y2)两点,与x轴的正半轴相交于点D,与y轴相交于点C.当ab=1时,△AOB一定是直角三角形.
我们曾改编过如下一道变式考题安排学生练习,这里可附出这一素材:
题3:(变式题)如图4,直线y=kx+b(b>0)与抛物线y= ax2相交于A(x1,y1)、B(x2,y2)两点,与x轴的正半轴相交于点D,与y轴相交于点C.
(2)在(1)的条件下,求证点(y1,y2)在反比例函数y=的图像上.
(3)小乐经过演算发现:当ab=1时,△AOB一定是直角三角形.请判断“小乐发现”的真假,并说明理由.
教学手记:前两问只是题2的简单数据的改编,第(3)问则引导学生走一般,说明理由.以下是一个优秀学生给出的解法(如图6),思路能够贯通,但在处理“y1y2= -x1x2”这一步时略显跳跃.
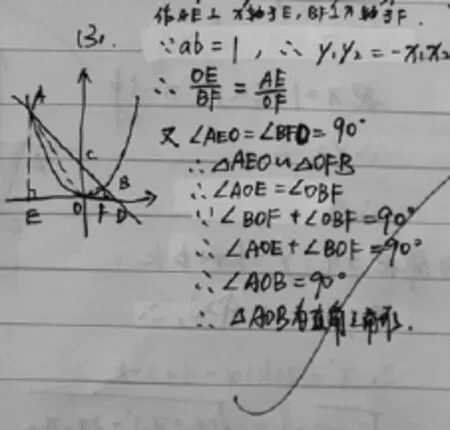
图6
题4:(2014年四川宜宾,有精减)如图7,已知抛物线y=x2+bx+c的顶点坐标为M(0,-1),与x轴交于A、B两点.设正比例函数y=kx的图像与抛物线交于C、D两点,连接MC、MD,求证MC⊥MD.
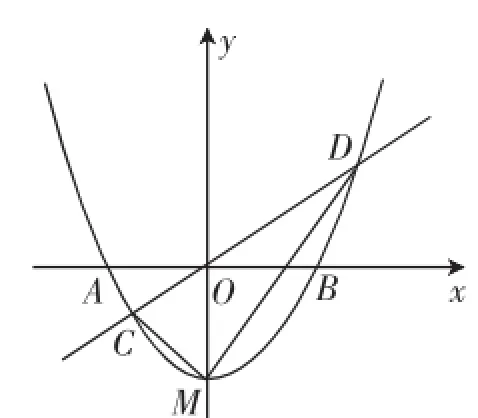
图7
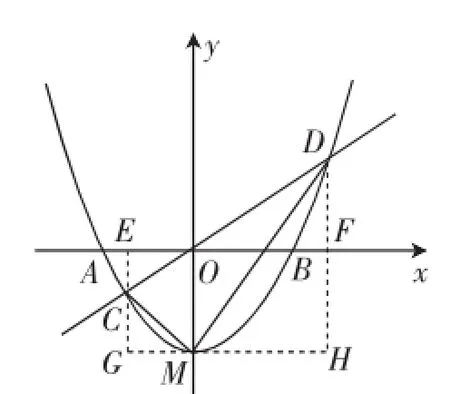
图8
思路简述:如图8,分别过点C、D作y轴的平行线,交x轴于E、F,过M点作x轴的平行线,交EC于G,交DF于H.
设D(m,m2-1)、C(n,n2-1).联立抛物线、直线方程转化为一元二次方程:y=x2-kx-1.这样由根与系数的关系得mn=-1.CG=yC-yG=n2-1-(-1)=n2,DH=yD-yH=m2-1-(-1)=m2,于是CG·DH=m2·n2=1,于是GM·MH=CG·DH,从而得出△CGM∽△MHD,即可贯通思路.
结构反思:可以发现,题4的证明思路与题2、题3是一致的,只是题4将x轴向上平移了1个单位而已,证明思路仍然是构造一组直角三角形相似.
二、关于中考专题复习的初步思考
上面这个素材是我们在中考二轮专题复习时的一些积累,主要还是来自于解后的教学手记,这启示着我们关于中考专题复习的一些思路.
1.专题复习的切入口宜小,不宜广种薄收,力争一课一得.
我们注意到不少教辅资料上对于中考专题复习常常划分为:最值问题、新定义问题、设计优化问题、图表信息问题、实际应用问题、阅读理解问题、开放探究问题、动态探究问题等形式化、表面化的分类专题.比如,一节阅读理解题的专题复习中所选例题之间只是形式上有阅读理解的外貌,却在各自解法上南辕北辙,缺少内在的关联.我们认为这种广种薄收的专题复习虽然十分流行,但是值得商榷,有很大的改进空间.上文中我们把一类形式不同的综合题归到一个小专题进行研究,就是从解题思路、问题结构上关联思考,训练学生的眼力、洞察具有相同结构的难题.
2.专题复习的习题需精选,削枝强干,突出专题训练重点.
中考复习课通常只有40分钟左右,而一道综合题的答题时间从命题预设的角度也在30分钟以上,所以中考专题复习如果定位在综合题的讲评辅导,对入选试题需要进行删减,特别是要削枝强干,突破本节课训练的重点.比如,上文中题4原是一道中考压轴题(设有系列3个小问),但我们将其选入专题复习,为了使其与前面3个试题具有高度相关性,我们将其删减,保留了第(3)问的求证方向,也就突出了本专题的训练重点.
3.专题复习后需变式再练,简单改编与拓展思考相结合.
由于中考二轮复习常常聚焦于中考较难题、把关题、压轴题,这些试题往往源于各级模考、中考试题中承载区分功能的难题,所以仅仅是在课堂上合作探究、贯通思路,根据教学经验,仍然有很多学生难以当堂消化理解,所以必要的跟进变式再练十分重要.这也是我们在上面提供“题3”的原因,根据我们对题3训练效果的反馈,学生对简单改编的前两问训练效果还不错,但是最后一问的拓展思考,全班只有少数几个学生能贯通思路或看出解题方向,但在演算上仍然缺少规范、严谨的步骤.
三、写在后面
中考复习“岁岁年年花相似,但年年岁岁花不同”.因为中考复习没有课标的规定、缺少教材的支持,教学内容需要靠教师自主研发,这就给广大教师带来了专业自主的空间,能否使多年来的“八股化”题型复习走向更具内在关联的微专题复习,是值得深入思考的研讨方向.我们的努力还很初步,期待更多的批判与实践跟进.
1.何明.由博返约,追求简洁——一道“双曲线”综合题的命题过程[J].中学数学(下),2015(11).
2.章建跃.“题型+技巧”的危害[J].中小学数学(高中版),2010(11).
3.刘东升.我们需要怎样的“问题”驱动课堂——由美国莎维女士执教的函数图像课说起[J].教育研究与评论(课堂观察版),2016(11).
4.王友峰.专业自主增设内容,回看陈题洞察结构——九年级“探究四点共圆”教学设计与解读[J].中学数学(下),2016(12).
