双层桨搅拌槽的混合过程研究

徐 金, 逄启寿, 郜飘飘， 罗 松

(江西理工大学 机电工程学院， 江西 赣州 341000)

双层桨搅拌槽的混合过程研究

徐 金, 逄启寿, 郜飘飘， 罗 松

(江西理工大学 机电工程学院， 江西 赣州 341000)

为了提高双层桨酸溶搅拌槽的混合速率，本文利用数值模拟的方法对双层桨以及改变结构参数后的搅拌桨的混合过程进行了研究。结果表明：桨叶直径、叶片角度、挡板宽度等五个结构参数对混合过程的影响不同，其中桨叶直径的增大能有效缩短混合时间，叶片角度的增加主要影响搅拌槽内的流场流型，挡板宽度对混合过程基本无影响。

混合过程； 数值模拟； 结构参数

0 引言

搅拌混合过程的研究是设计搅拌设备的重要依据，一直是国内外学者所关注的问题。计算流体力学(CFD)方法因其较实验方法具有操作简单、耗时较短、性能预测强、内部流场可视化等优点广泛应用在搅拌混合过程的研究中。施力田等[1]采用数值模拟的方法对双层涡轮桨搅拌反应器内流体的流动和混合进行了研究，并试验测试了混合过程，两个结果吻合良好。赵静等[2]研究了三层组合桨搅拌槽内流场，通过改变桨的三个结构参数得到了4种不同流型。逄启寿[3]对直斜组合桨不同安装顺序下的混合过程进行了数值模拟，并分析了加料点和监测点的位置对混合时间的影响。

本文利用数值模拟的方法对双层折叶桨以及改变结构参数后的搅拌桨的混合过程进行研究。分析了初始桨的示踪剂扩散过程和响应曲线，并重点讨论了双层桨酸溶槽的5个结构参数对混合过程的影响。

1 研究对象

1.1 几何模型

以赣州某企业的钕铁硼酸溶搅拌槽为研究对象，该搅拌槽为弧形底的圆桶，桶径D=3 000 mm，桶高H=3 000 mm，有效液面高度H1=2 800 mm。内部有对称分布的4块挡板，挡板宽度Wb=250 mm，挡板离桶壁距离Sb=50 mm。初始搅拌桨为双层折叶桨，两层桨叶交叉90°，桨叶直径d=1 200 mm，桨叶宽度b=120 mm，叶片角度θ=60°，层距SP=500 mm，下桨叶离槽底部距离Sc=600 mm。

1.2 参数设计

本文以初始桨叶和挡板宽度结构尺寸作为基础并根据多层桨叶和挡板宽度的尺寸设计推荐公式，选取了五个结构参数：桨叶直径d、叶片角度θ、挡板宽度Wb、下桨叶离底部距离Sc、两桨叶之间的层距SP，经过计算后在合适的取值范围内各结构参数选取五组数值作为研究对象。各结构参数的选取值如表1。

2 数值模拟方法

2.1 网格划分

利用GAMBIT软件采用非结构化网格的方式对三维模型进行网格划分。由于搅拌桨的结构不规则，因此，划分桨叶旋转区域和外部桶体静止区域的网格时采用不同增长率，同时对搅拌旋转区域内进行适当的加密处理，提高该区域的计算精度。搅拌槽整体网格划分结果如图1所示。

2.2 模拟计算方法和物料属性

模拟计算方法与文献[3]中提供的方法一致。采用多重参考系法处理旋转区域与静止区域，模拟选用标准k-ε模型，采用隐式分离求解器，先进行稳态求解流场，待流场稳定后，加入示踪剂进行非稳态

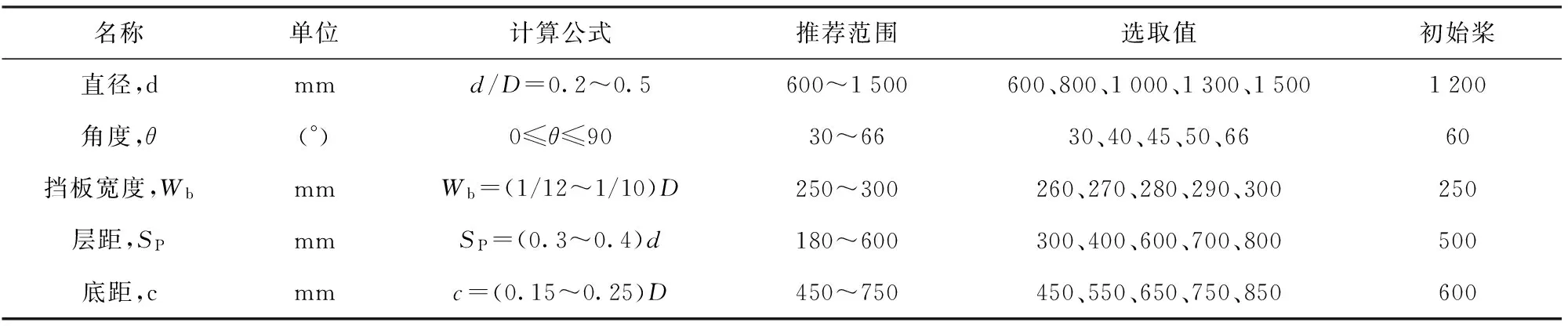
表1 搅拌桨参数选取值

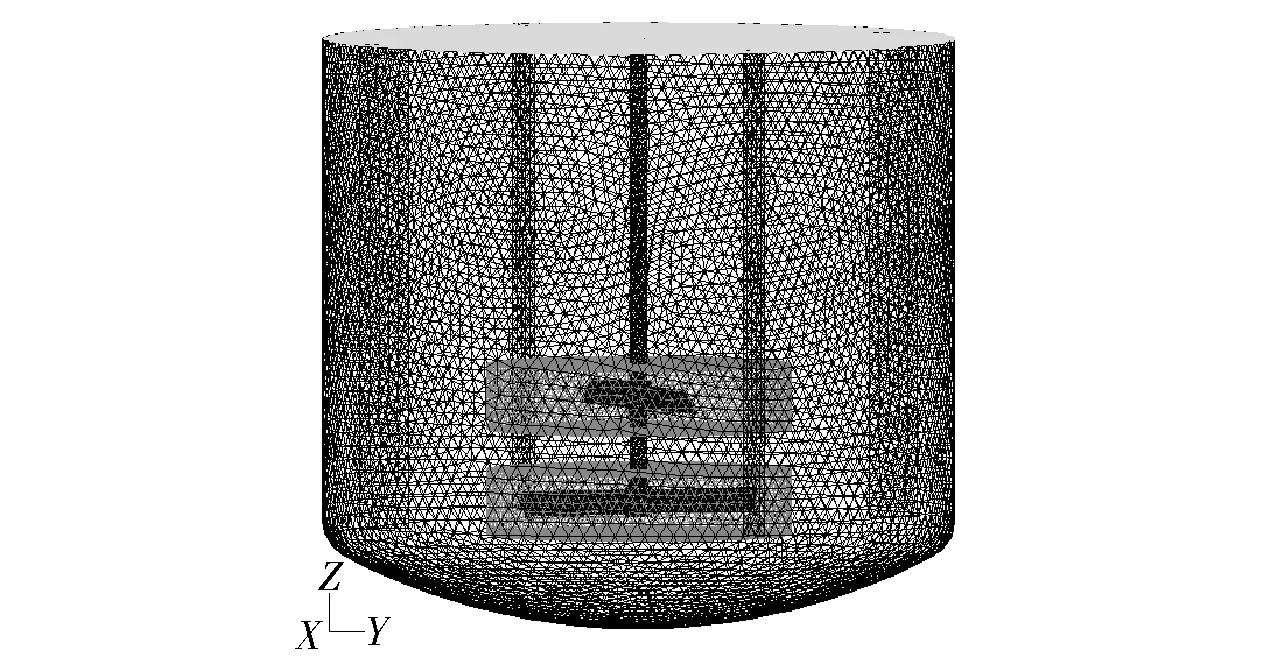
图1 搅拌槽整体网格划分

求解浓度场。示踪剂一般选能和工作介质互溶的物质，通常选用NaCl或KCl[4]，本文模拟选用NaCl作为示踪剂材料，其密度(20 ℃)为1 186 kg/m3，粘度μ=2.3×10-3Pa·s。它的加入是通过设置好的投料点作为球心，将半径为100 mm的球体所包含的区域作为示踪剂，将其浓度值定义为1，槽内其他区域浓度值定义为0。利用Fluent初始化功能中的补丁功能，通过补丁的方式加入到计算当中。

物料属性：本模拟选用的工作介质为水和甘油的混合物，参照实际生产物料溶解后的料液宏观上类似污水，粘度范围一般在5×10-3Pa·s～10×10-3Pa·s之间，根据化学化工物性手册- 有机卷查得58%甘油水溶液其密度(20 ℃)为1 148.3 kg/m3，粘度μ=9.586×10-3Pa·s。

2.3 模拟条件与参数

混合时间是描述混合过程的一个重要参量，它是通过监测槽内设定点的示踪剂浓度值得来的，当所有设定点的示踪剂浓度值达到稳定浓度的±5%且后续波动不超过该范围[5]，则认为最后达到该浓度值的监测点所需时间为最终混合时间。本文选取靠近液面的一点T作为加料点。在相邻两挡板之间选取四个监测点，分别为P1、P2、P3、P4，且各监测点离桶壁距离相等。监测点及加料点具体分布如图2所。

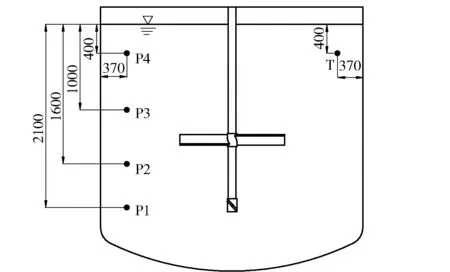
图2 监测点与加料点位置示意图

3 结果与讨论

3.1 示踪剂扩散分析

图3是初始桨在转速为75 rpm下不同时刻的示踪剂扩散云图，云图观测面是处于相邻两挡板之间夹角45°的中间面。由于示踪剂在前期扩散运动不是太明显，因此，云图截取时间选10 s～35 s，时间间隔为5 s，在该段时间内示踪剂扩散运动较为剧烈和明显。从图中明显看到示踪剂扩散表现出轴向循环排液的特点，液面加料点处的示踪剂首先向叶轮区靠近，后沿桨叶向下排液方向运动碰触槽底后反向沿槽壁向上运动，到达液面处后又沿搅拌轴向叶轮区运动形成一个大循环，这与轴向搅拌桨的“单循环”流动相一致；由于示踪剂的扩散与速度场密切相关[6]，从t=25 s时刻的示踪剂扩散云图可知搅拌轴远离桨叶的上部分区域介质流速比较低，示踪剂向此处的扩散主要靠浓度差。

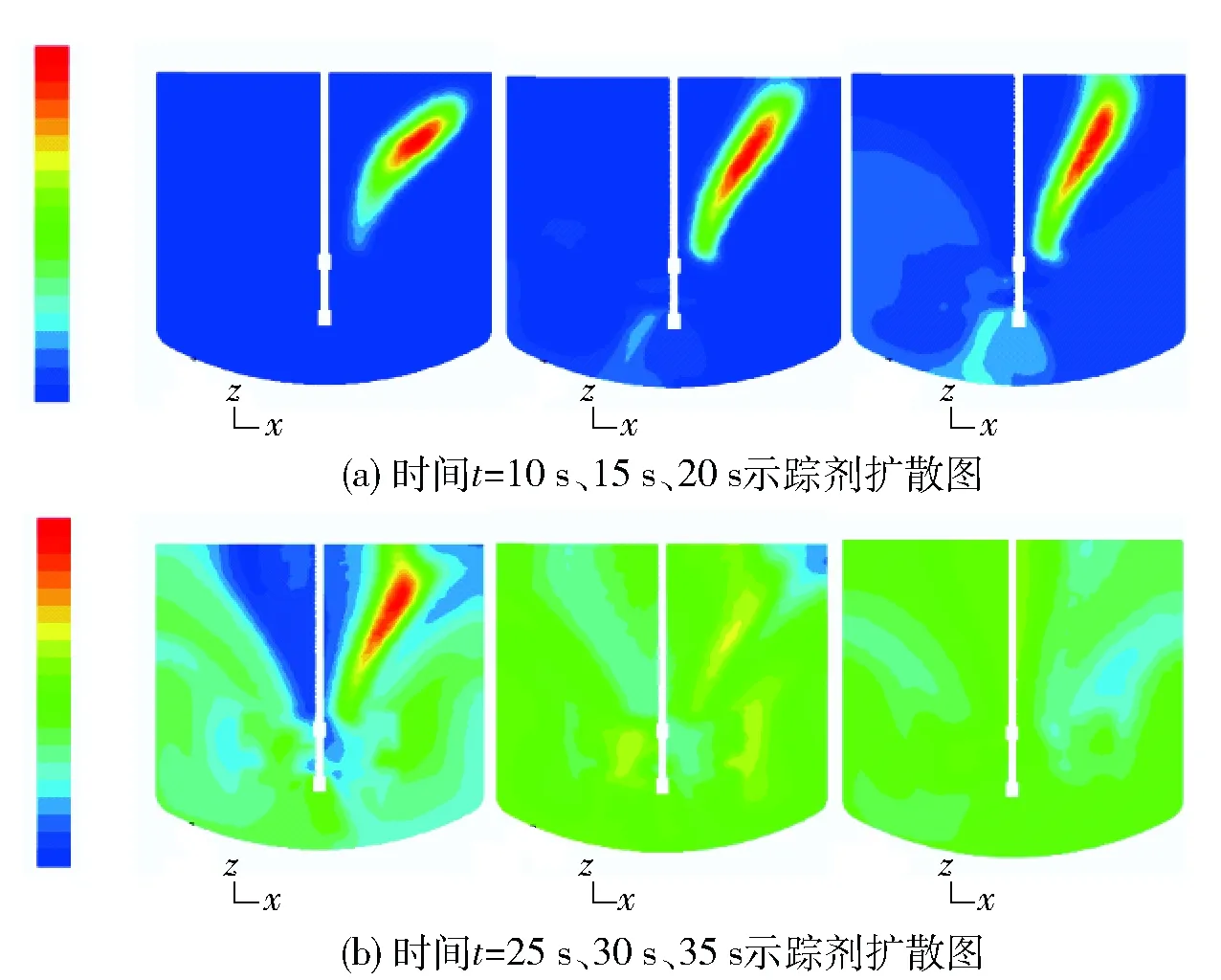
图3 不同时刻示踪剂扩散云图

3.2 混合时间与混合准数分析

根据设置的监测点，通过监测得到每一时刻下的浓度值进而绘制出时间浓度曲线，得到混合时间，由于监测数据较多，在这里只给出了初始桨叶的浓度时间变化曲线，如图4所示。其余监测数据均在表2中给出。

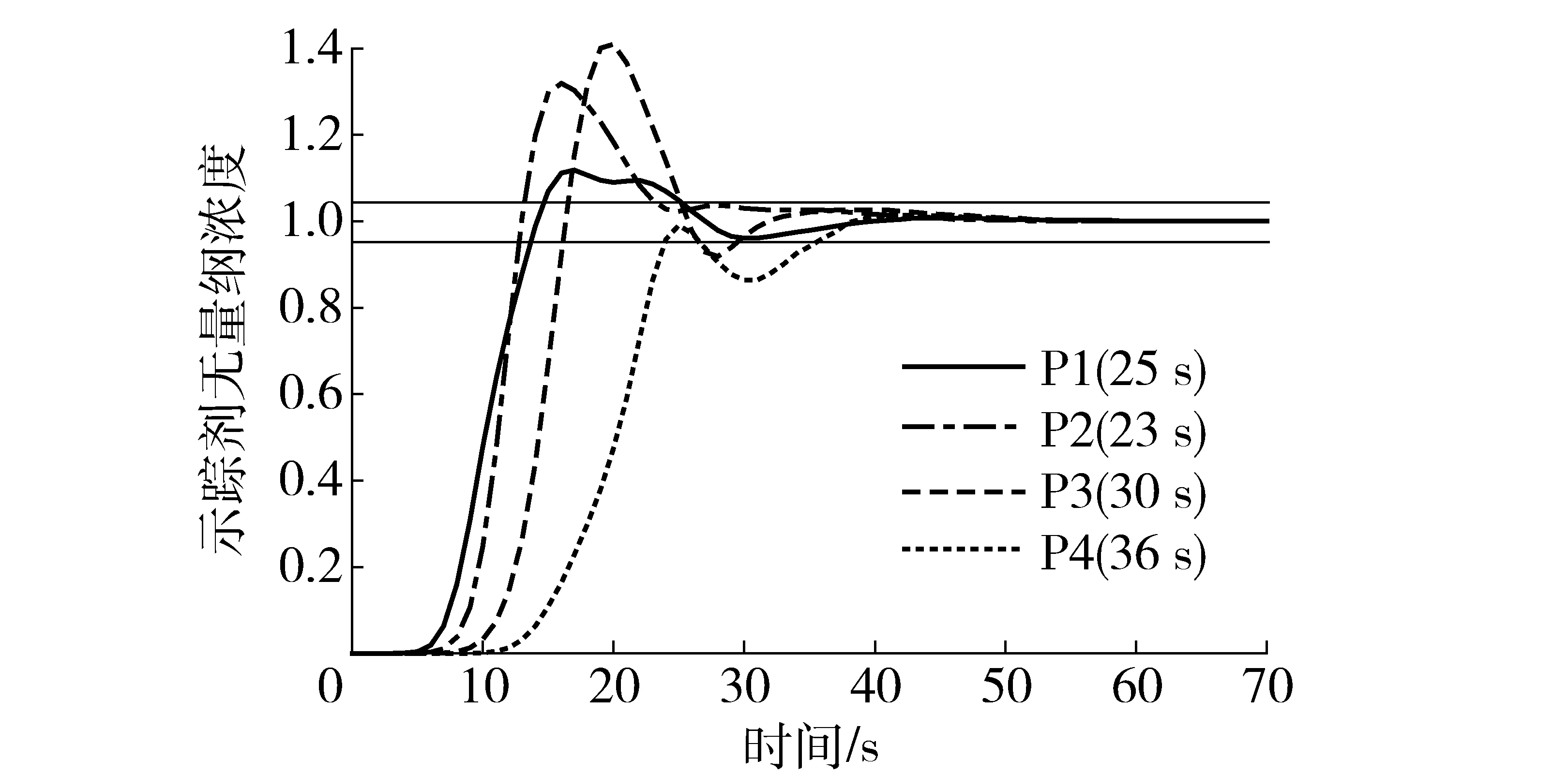
图4 监测点浓度随时间变化曲线

从图4中可以看出，在同一槽体内各监测点所得到的浓度响应曲线不相同，虽然都有明显的浓度峰值，峰值的大小不同，出现的时刻也不同，P1点和P2点基本同时出现峰值，随后P3点出现峰值，最后P4点出现峰值，这与前面的浓度扩散云图相一致，再次证明了槽内的流场是“单循环流”。由于桨叶结构尺寸改变而引起槽内流场变化，使得在同一位置上的监测点所获得的浓度响应曲线也不尽相同，监测点得到的混合时间也不同。

为了更好地对混合效果进行评价，在这里引入搅拌桨的混合准数：通常用无量纲为一的物理量来表示，由搅拌桨转速与混合时间的乘积而得到[7]：

Tm=θmN

(1)

式中：θm——最终混合时间，s；

N——搅拌转速，rpm。

Tm的物理意义为达到所设定的混合效果，搅拌桨需要旋转圈数的数值越小，则说明搅拌桨的混合速率越高。因此，混合准数也常作为评价搅拌桨混合性能好坏的指标之一。各变量下的混合准数计算结果见下表2。

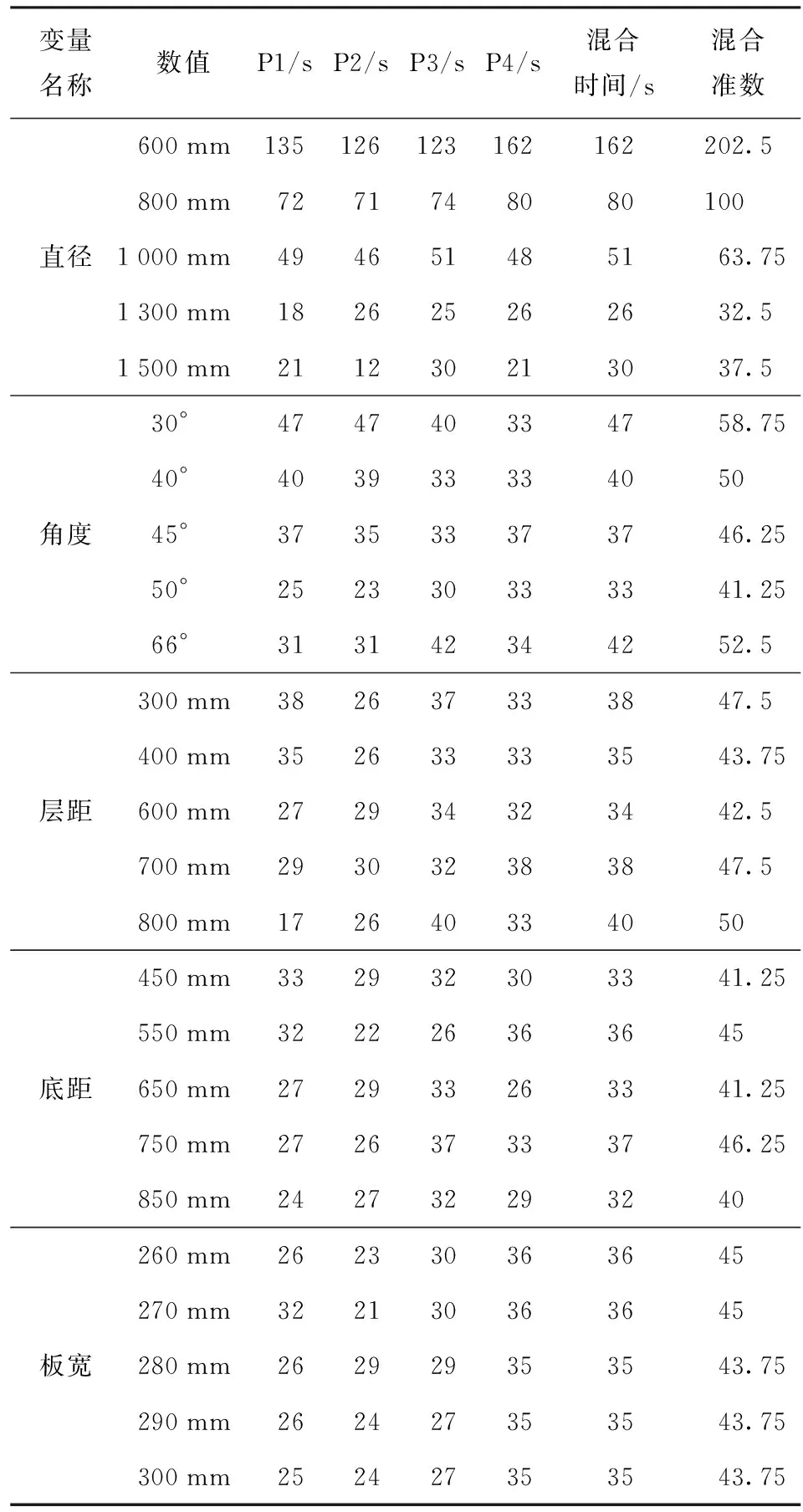
表2 各监测点所得混合时间与 混合准数的计算结果

从表2中可以看出，桨叶直径对各监测点的混合时间影响较大，直径<1 000 mm时，远离桨叶的监测点P4的混合时间明显比其他监测点的混合时间长，而直径≥1 000 mm时此现象消失；桨叶直径增加能有效缩短最终混合时间且变化范围差值接近100 s，但缩短趋势逐渐减弱且未随着直径增加而一直减小，说明直径对混合时间的缩短作用在一定的尺寸范围内。在角度影响下所得到的最终混合时间作用规律类似直径变化产生的效果，角度对混合时间缩短作用同样存在着一个的范围；角度为30°时P4点最先混合均匀，这是因为加料点与P4点处在同一水平面，此角度下流场表现为切向流为主，随着角度的增加，最短混合时间由P4点逐渐变到P1点，说明切向流逐渐转为轴向流，这与文献[8]结果一致。随着层距的增加最终混合时间呈现出先减小后增大的“波谷”状，这与文献[9]结果一致。随着底距的增加，最终混合时间出现“M”状，在底距为550 mm和750 mm处最终混合时间比较长，混合效率比较低。挡板宽度对最终混合时间基本无影响，且最终混合时间均由离桨叶最远的监测点P4决定。

由表2中计算得到的混合准数可以看出，在桨叶直径为1 300 mm的情况下大约只需要旋转33圈即可达到规定的混合效果，而直径在为600 mm的情况下则要转203圈才能达到，相差近6倍关系。同时混合准数的最小与最大值均在直径组当中出现，可见直径对于混合速率的影响是非常大的。折叶角度在本文所选取的最大值66°时，其达到混合均匀要求时需要转动的圈数却不是该变量组中最少的，角度在30°-50°内增加时对于混合速率有一定的提高作用，当折叶角度超过这个范围时混合速率没有提高反而出现下降。层距在300 mm～600 mm时混合速率会随着层距增大而出现小幅提高，在超过600 mm同样出了混合速率下降的情况。

4 结论

(1)在转速不变的情况下，桨叶直径增大，叶片末端线速度增大，湍动能增大，因此能有效缩短最终混合时间，提高混合速率，但其作用效果逐渐降低，且在一定的尺寸范围内。

(2)随着折叶桨叶片角度的增加，流场逐渐从切向流过渡到轴向流，这和叶片的排液方式相关，其和层距对混合速率的影响类似，都存在一个最佳值。

(3)挡板宽度在推荐值范围内对混合速率基本无影响，当超过推荐值时对混合速率的影响还有待研究。

[1] 施力田,高正明,闵健.双层涡轮桨搅拌反应器内混合时间的大涡模拟[J].华东理工大学学报:自然科学版,2006,32(3):352-356.

[2] 赵静,程先明,高正明.组合桨液相搅拌槽内流动特性的实验研究及数值模拟[J].北京化工大学学报:自然科学版,2011,38(3):22-27.

[3] 逄启寿,罗松,徐金.直斜组合桨叶片不同位置顺序的流场数值分析[J].机械设计与制造,2016,(4):234-237.

[4] Satish D. Shewale, Aniruddha B. Pandit. Studies in multiple impeller agitated gas-liquid contactors[J]. Chemical Engineering Science,2006,61(02):489-504.

[5] 梁瑛娜,高殿荣,拜亮.双层桨搅拌槽内层流流场与混合时间的数值模拟[J].机械工程学报,2015,51(16):185-195.

[6] 苗一,潘家祯.轴流式搅拌桨搅拌槽内混合时间的数值模拟[J].合成橡胶工业,2007,30(1):5-9.

[7] 陈志平,章序文,林兴华.搅拌与混合设备设计选用手册[M].北京:化学工业出版社,2004,53-54,109-115.

[8] 龚姚腾,曾令挥,肖顺根.不同搅拌形式对稀土萃取槽内搅拌效果的影响模拟分析[J].湿法冶金,2009,28(108):49-52.

[9] 吴富姬.搅拌混合槽内混合过程的数值模拟[J].湿法冶金,2014,33(4):328-331.

Research of mixing process in stirred tanks with dual impeller

XU Jin, PANG Qi-shou, GAO Piao-piao， LUO Song

To increase the mixing rate of acid-soluble stirred tanks with dual impeller, this paper studies on the mixing process of dual impeller and agitating impeller after adjusting structure parameters by numerical simulation. The results show that five structure parameters, such as impeller diameter and angle, width of baffle had different effects on nixing process. The increase of the impeller diameter could significantly shorten the mixing time. The impeller angle mainly affects the flow field of the stirred tank. The width of baffle hardly effects on mixing process.

mixing process; numerical simulation; structure parameter

徐 金(1990—),女，山东沂南人，硕士，主要研究方向：机械制造与冶金设备。

2016-04-21

TQ051.7

B

1672-6103(2017)01-0046-04