基于人工蜂群算法的柔性工艺与车间调度集成优化

宋栓军，杨佩莉，石雯丽

(西安工程大学 机电工程学院，西安 710048)

(*通信作者电子邮箱447090664@qq.com)

基于人工蜂群算法的柔性工艺与车间调度集成优化

宋栓军，杨佩莉*，石雯丽

(西安工程大学 机电工程学院，西安 710048)

(*通信作者电子邮箱447090664@qq.com)

为实现柔性工艺与车间调度集成优化，在考虑工件特征的加工工艺、次序及加工机器的柔性基础上，以最小化最大完工时间为优化目标，提出一种基于交叉变异的人工蜂群算法。该算法针对柔性工艺与车间调度集成问题的离散性特征，对工艺路线进行序列编码，工件调度采用基于工序的编码方式。通过工艺种群与调度种群的交叉变异操作，分别使采蜜蜂及观察蜂进行局部寻优，侦查蜂进行全局寻优，以此提高算法性能。在此基础上用两部分测试实例分别验证了集成研究的必要性及改进算法的有效性。

柔性工艺规划；车间调度；人工蜂群算法

0 引言

工艺规划与车间调度集成(Integrated Process Planning and Scheduling，IPPS)是制造系统中急需解决的关键问题之一。在传统的企业生产过程中，工艺规划和车间调度往往被当作独立的系统进行研究，导致了工艺与调度的脱节[1]。如果将工艺规划和车间调度系统进行集成，则可避免制造资源的浪费，优化生产节拍，提高制造系统的工作效率[2-3]。

Chryssolouris等[4]首先提出了工艺规划与车间调度集成的构想；之后Beckendorff等[5]在二者集成时考虑了工艺路线的柔性问题，首次在IPPS问题中考虑到工艺的柔性特点。上述研究使学者们开始关注工艺与调度集成问题的研究。刘倩雯[6]利用人工蜂群算法(Artificial Bee Colony， ABC)求解作业车间调度问题，通过仿真实验验证了算法的有效性；瞿璨[7]将人工蜂群与模拟退火算法相结合求解面向绿色制造的工艺路线优化，通过算例测试获得了高效稳定的解。这两个研究都是将工艺与调度系统进行独立研究。吕盛坪等[8-9]对工艺规划与车间调度集成现状和趋势以及集成模型作了分析，为IPPS问题的后续研究奠定基础；崔晓康等[10]提出三阶段工艺与调度的集成方法，并通过实例验证了方法的有效性；王进峰等[11]对蚁群算法中信息素挥发速度以及蚂蚁转移概率进行改进，将其应用于IPPS优化中，最后通过仿真实例表明了算法的有效性。这四个研究都是针对单目标IPPS问题，并且没有考虑工艺的柔性特征。Liu等[12]提出一种多目标微型人工蜂群算法，对有约束条件的多目标弹性作业车间调度问题求解，优化目标是尽量减少机器的工作量以及生产周期；文笑雨[13]采用蜜蜂繁殖优化算法，分别对多目标及多目标不确定性IPPS问题进行研究，之后研究了多目标IPPS决策方法，最后通过实例验证算法的有效性。这两篇文章都是针对多目标IPPS问题进行研究。从上述研究看，虽然针对IPPS的研究较多，但考虑到工艺柔性的较少；人工蜂群算法本身具备全局收敛优势[14]，通过三种蜂的转换，借助启发式搜索策略，具有很好的局部搜索及全局寻优的能力，因此本文在研究以上方法的基础上，考虑到工件的柔性特征，提出了一种基于交叉变异的人工蜂群算法，对柔性工艺与车间调度集成(Integrated Flexible Process Planning and Scheduling，IFPPS)问题进行优化求解，并通过工艺的序列编码及基于工序的调度编码使算法能够适应IFPPS问题的离散性特征，提出工艺种群与调度种群的交叉变异操作，不仅使产生的新解能够满足工序的顺序约束，还能够通过此算法最终获得更优的加工路线和调度方案。

1 IFPPS优化数学模型

本文以单目标IFPPS问题为例，以加工任务的最大完工时间(makespan)最小为目标进行优化研究，车间调度问题为作业车间调度。在建立优化数学模型前作如下假设[15-16]：

1)初始时刻，制造车间的所有机器均可正常使用；

2)在进行排产优化时，不同工件相互之间没有优先级，不同工件的加工工序之间也没有优先级，同一工件的各个工序之间存在优先级；

3)在同一时间，每台机器仅可加工一道工序；

4)所有工序的加工时间是指其实际加工与其准备加工时间之和。

基于以上假设，本文研究的IFPPS数学模型如下所示，其中：A表示一个非常大的正数；n表示需要加工的工件总数；m表示机器数；gi表示工件i可选工艺路线数；pil表示工件i的第l条工艺路线中的工序数；oijl表示工件i在第l条工艺路线下的第j道工序；k表示工序oijl的可选加工机器；bijlk表示工序oijl在机器k上的开工时间；tijlk表示工序oijl在机器k上的加工时间；cijlk表示工序oijl在机器k上的完工时间；ci(j-1)lq表示工序oijl的上一道加工工序oi(j-1)l在其加工机器q上的完工时间；cxylk表示机器k上排在工序oijl紧前加工的工序oxyl的完工时间；zi(j-1，j)l(q，k)表示工序oi(j-1)l的加工机器q转向工序oijl的加工机器k的机器转换时间；ci表示工件i的完工时间；vijlk表示工序oijl在机器k上的加工成本；

Yijlpqsk=

目标函数如式(1)所示：

f1=min{makespan=max(ci)}

(1)

约束条件如式(2)～(10)所示：

1)工件i第l条工艺路线的首道加工工序的最早完工时间大于或等于其加工时间：

(ci1lk×Zi1lk×Xil)+A(1-Xil)≥(ti1lk×Zi1lk×Xil);

∀i∈[1,n], ∀l∈[1,gi], ∀k∈[1,m]

(2)

2)工件i第l条工艺路线的末道加工工序的最早完工时间小于或等于工件i的最大完工时间：

(cipillk×Zipillk×Xil)-A(1-Xil)≤makespan;

∀i∈[1,n], ∀l∈[1,gi], ∀k∈[1,m]

(3)

3)一个工件同一时刻仅可有一道工序被加工：

(cijlk×Zijlk×Xil)-(ci(j-1)lk1×Zi(j-1)lk1×Xil)+

A(1-Xil)≥(tijlk×Zijlk×Xil); ∀i∈[1,n],

∀j∈[1,pil], ∀l∈[1,gi], ∀k,k1∈[1,m]

(4)

4)每台机器同一时刻仅可加工一道工序：

(5)

5)工件i仅可选取一条工艺路线输入到调度系统：

(6)

6)一道工序仅可选取一台加工机器：

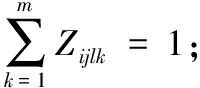
(7)

7)所有工序的开工时间大于或等于0：

bijlk×Zijlk×Xil≥0; ∀i∈[1,n], ∀j∈[1,pil],

∀l∈[1,gi], ∀k∈[1,m]

(8)

8)工序oijl在机器k上的完工时间等于其开工时间与加工时间之和：

cijlk×Zijlk×Xil=(bijlk+tijlk×Zijlk×Xil; ∀i∈[1,n],

∀j∈[1,pil], ∀l∈[1,gi], ∀k∈[1,m]

(9)

9)工序oijl在机器k上的开工时间等于工序oi(j-1)l在其加工机器q上的完工时间与工序oi(j-1)l的加工机器q转向工序oijl的加工机器k的机器转换时间之和以及之前最后一个在加工机器k上进行加工的工序完工时间中较大的数：

bijlk=max(oi(j-1)lq+zi(j-1, j),l(q,k),cxylk); ∀i∈[1,n],

∀j∈[2,pil], ∀l∈[1,gi], ∀k,q∈[1,m]

(10)

2 IFPPS优化算法设计

2.1 柔性工艺调度的编码及解码

1)柔性工艺规划编码及解码。

根据工艺的柔性特征，本文创新性地提出一种序列编码方式对工艺规划部分的各个序列进行编码，表1为工件1的加工工艺信息。对工件1加工工艺信息进行序列编码，编码结果如图1所示。

表1 工件1加工工艺信息表

图1 工件1加工工艺信息序列编码方案

特征序列中的第n个数字m表示特征m的加工顺序是n；工序序列中的第a个数字b表示工件第a个特征选择第b种可选工艺加工；机器序列中的第i个数字j表示第i个工艺用j号机器进行加工。用序列编码方式很容易实现解码，首先根据特征序列，可以获得工件1各个特征的加工顺序为F4—F2—F1—F6—F3—F5；然后根据工序序列获得各特征所选的加工工艺，再按照特征顺序进行排列，可以得到工件1具体的加工工序序列为O5—O2—O1—O7—O4—O6；最后根据机器序列，结合加工工艺得到各个工艺所选择的加工机器，从而确定出该工件的一条可行工艺路线O5(M3)—O2(M4)—O1(M1)—O7(M1)—O4(M1)—O6(M4)。

2)车间调度编码及解码。

在车间调度编码的相关研究中，用得最多的是基于工序的编码方法，本文也利用此方式对个体进行编码[17]。设一个企业制造车间中的待加工工件数为4，在初始工艺路线中按照适应度函数值挑选出各工件较优的路线后，就可以知道要加工的工序总数。假设工件1共包含6道工序，工件2包含5道工序，工件3包含3道工序，工件4包含5道工序， 那么[1 1 2 3 4 4 2 4 1 1 2 4 2 1 1 4 2 3 3]就为一种可行的调度编码方案。在此方案中，工件序号出现的次数与其所包含的工序数相同，例如工件1包含6道工序，那么1就在调度编码方案中一共出现6次。此外方案中第6个位置上的4是从左到右数数字4出现的第2次，所以第6个位置代表了工件4的工艺路线中第2道要加工的工序。

由于本文选用的优化目标为最小化最大完工时间，属于正规调度指标，并且基于工序的编码方式产生的调度方案均为可行的调度方案，因此选择使用文献[18]中的贪婪解码方法将编码方案解码为活动调度类型。贪婪解码方法的具体步骤可由文献[18]获得，此处不再赘述。

2.2 基于交叉变异的人工蜂群算法

使用人工蜂群算法求解IFPPS优化问题时，每个蜜源代表一个可行的调度方案，每个蜜源的参数从开始到结束代表某个任务中各工序可能的工作顺序，因此可由改变蜜源参数来改变各工序的加工顺序，并计算其完工时间，寻找最优方案[14]。为了保证种群的多样性，本文对基本人工蜂群算法进行改进，提出了一种基于交叉变异的人工蜂群算法，并设计了算法求解的主要内容。

1)蜂群初始化。

由于工艺及工件顺序的表示需要是一个大于或等于1的整数，而基本人工蜂群算法中，种群初始化方法是产生连续的随机数，会出现非整数的情况，因此本文对人工蜂群算法的初始化方式进行了改进。通过Matlab程序直接产生符合要求的可行性随机解，在工艺规划阶段，由于工序有次序约束，因此随机生成的特征序列可能不符合要求，采用文献[18]中的约束调整方法对特征序列进行调整，使生成的各工件的初始工艺路线可行。由于基于工序的编码方式不会生成不可行解，因此本文对车间调度部分的初始化蜂群进行随机生成，然后将编码方案解码后，计算蜂群中每个蜜蜂所代表的IFPPS方案的完工时间。

2)工艺种群交叉变异操作。

为了使工艺规划系统可以源源不断地为调度系统输入各个工件不同的工艺路线方案，在进行柔性工艺规划与车间调度集成优化时，集成优化总流程每迭代一次，就需要对工艺种群更新一次。针对工艺的序列编码方式，本文提出工艺种群交叉变异操作对其进行种群更新，保证种群的多样性。

在工艺种群交叉变异操作中，使采蜜蜂和观察蜂利用变异操作进行局部搜索。具体步骤如下：

步骤1 将特征序列中两个随机位置的数值进行交换，产生新的特征序列，并通过约束调整方法对其进行调整，使其符合特征之间的次序约束条件；

步骤2 将工艺序列中一个随机位置所选择的加工工艺转变成另一种可选加工工艺；

步骤3 将机器序列中一个随机位置所选择的加工机器转变成另一种可选加工机器。

在工艺种群交叉变异操作中，使侦查蜂利用交叉操作进行全局搜索。当侦查蜂进行全局搜索随机产生新蜜源时，由于算法初始化已经产生了符合工件特征顺序约束的序列，优化过程就是适当调整这个序列中参数的顺序，以得到一个能够使某个目标值达到最优的顺序，而不需要重新生成任何参数或信息，因此采用两点交叉操作来对其进行调整，能够使产生的新序列满足工件的特征次序约束。在侦查蜂进行交叉操作时，分别对工件的三个序列进行两点交叉操作，产生新的可行工艺路线。在文献[2]的基础上，对其特征序列交叉操作进行改进，将原始的复制交叉点中断的参数信息到新的特征序列相应位置改为复制交叉点两端的参数信息到新的特征序列的相应位置，此方式可以确保生成的新的可行解满足工序的次序约束条件，具体步骤如下：

步骤1 随机挑选两个蜜源(蜜源1、蜜源2)，对其三个序列分别进行交叉操作。

步骤2 在蜜源的序列中随机选择两个交叉点，特征序列用步骤3交叉操作，工艺序列和机器序列用步骤4进行交叉操作。

步骤3 将特征序列1交叉点两端参数信息复制给新特征序列的相应位置，删掉特征序列2中新特征序列中已有的特征数值，将特征序列2中剩余的数值按顺序依次填入到新特征序列的空位置中，这样就生成了新的特征序列。

步骤4 将工艺序列1交叉点中断参数信息复制到新工艺序列的相应位置，将工艺序列2的交叉点两端的参数信息按顺序填入新工艺序列的空位置中，这样就生成了新的工艺序列，机器序列同工艺序列。

3)调度种群交叉变异操作。

在调度系统的优化流程迭代中，需要不断寻找新的调度方案，对调度种群进行更新。针对基于工序的调度编码方式，本文提出一种调度种群交叉变异操作进行种群更新。

在调度种群交叉变异操作中，使采蜜蜂及观察蜂利用变异操作进行局部搜索。即在原来的调度方案中，随机挑选两个不同的参数，将其位置进行互换，即可得到变异后的调度方案。

在调度种群交叉变异操作中，使侦查蜂利用交叉操作进行全局搜索。本文采用基于工序先后顺序的交叉操作[2]，具体步骤如下：

步骤1 在调度种群中随机挑选两个蜜源(可行解)；

步骤2 将工件集{1,2,…，n}随机划分为两个非空子集JobSet1和JobSet2；

步骤3 将蜜源1、蜜源2中与JobSet1相同的工件分别复制到新蜜源1、新蜜源2的对应位置，并保持顺序不变；

步骤4 将蜜源1、蜜源2中与JobSet2相同的工件分别复制到新蜜源2、新蜜源1中，并保持顺序不变。

以图1的编码方案为例，对上述蜜源进行交叉操作，结果如图2所示。

图2 基于工序先后顺序的交叉操作

3 IFPPS优化流程设计

本文采用集成式优化策略，以最大完工时间最小化为优化目标，由于人工蜂群算法中适应度值越大代表蜜源越好，因此使适应度函数等于目标函数的倒数，如式(11)所示,f是目标函数值，Fitness是适应度函数值。

Fitness=1/f

(11)

根据上述基于交叉变异的人工蜂群算法，对工艺规划系统和车间调度系统进行集成优化，最终确定各个工件的最优工艺路线和车间调度方案，具体流程如图3所示。

图3 优化策略流程

求解步骤如下：

步骤1 设加工工件数为n，根据各工件的工艺信息，初始化n个工艺种群。

步骤2 计算每个工件初始路线的适应度函数值，选择值最大的一条工艺路线。

步骤3 把各工件所选择的工艺路线输入车间调度系统。

步骤4 通过基于交叉变异的人工蜂群算法对车间调度系统进行优化，主要包含以下步骤:

1)根据工艺系统输送的工艺路线，初始化调度种群。

2)计算种群中所有个体的适应度值，并将值最大的调度方案记为最优调度方案。

3)判断是否达到车间调度系统优化的终止条件(达到调度系统最大迭代次数时算法结束)：如果是，就输出最优调度方案和各工件对应的工艺路线，并将其记为最优解，之后进行步骤5；不是就进行步骤4中的4)。

4)根据本文2.2节，利用调度种群的交叉变异操作产生新的调度种群。

5)转步骤4中的2)，迭代次数加1。

步骤5 根据基本ABC算法的贪婪准则更新最优解。

步骤6 判断是否满足集成系统的终止条件(达到集成系统最大运行次数时算法结束)，如果是，就输出最优解，不是就转到步骤7。

步骤7 根据本文2.2节工艺种群交叉变异操作方法，更新所有工艺种群。

步骤8 转到步骤2，迭代次数加1。

4 实例验证

本文进行了两组实例测试：第一组是为了验证柔性工艺规划与车间调度集成问题的必要性，对基于交叉变异的人工蜂群算法用于求解柔性工艺规划与车间调度集成和非集成的柔性工艺规划与车间调度(NonIFPPS)的结果进行比较；第二组是为了评估本文基于交叉变异的人工蜂群算法求解该集成问题的有效性，将本文算法求解结果与目前较好的其他算法进行比较。两部分实例算法参数设置如下：初始化蜜蜂总数NP=100(工艺系统与调度系统相同);采蜜蜂数量FoodNumber=NP/2(工艺系统与调度系统相同);侦查蜂数量SearchNumber=5(工艺系统与调度系统相同);集成最大运行次数RunTime=200;调度系统最大迭代次数maxCycle=50;蜜源最大开采次数Limit=5(工艺系统与调度系统相同)。

4.1 集成必要性验证

为了验证研究柔性工艺规划与车间调度集成问题的必要性，以六种工件在五台机器上加工的IFPPS问题为例进行分析，工件的参数信息如表1～3所示。通过Matlab对算法进行编程，柔性工艺规划与车间调度集成优化与非集成优化具体的测试结果对比如表4所示，集成式最优调度方案甘特图如图4所示。

从对比结果可以看出，单就工艺路线优化而言，非集成式中的工件1、工件2、工件4及工件5的最优工艺路线对应的加工时间小于集成式中对应的加工时间，而集成式柔性工艺规划与车间调度的最优调度方案的完工时间小于非集成式柔性工艺规划与车间调度。这是因为在传统的车间生产系统中，车间调度方案往往是在工艺规划之后进行的，在执行调度时，工艺规划必须限定在之前所产生的工艺路线之中，这样车间调度不可避免会受到工艺路线的约束，从而就会限制调度系统产生优化方案的效果。对柔性工艺规划与车间调度进行集成优化研究可以同时考虑工件的工艺路线优化和车间调度优化，不仅能够增加车间生产系统的柔性，同时能够减少工艺路线对调度优化的限制，因此即使单个工件的工艺路线不是最优，但是整体的调度方案却是最优的。由此说明研究柔性工艺规划与车间调度集成优化问题是十分必要的。

4.2 算法有效性验证

由于现有单目标工艺规划与车间调度集成优化研究中，缺乏同时考虑工艺规划多种柔性特征的实例，因此，选用Morad等[19]文章中的一个实例，该实例是5个工件在5台机器上进行加工，每个工件不存在加工工艺柔性及特征次序柔性，只存在加工机器柔性，并且工件在不同机器之间的转换时间忽略不计。具体工件的工艺信息如表5所示。

通过Matlab对实例进行编程，本文基于交叉变异的人工蜂群算法求得的优化结果为makespan=31，与其他优化算法求解结果对比如表6所示。从表6中可以看出，本文人工蜂群算法的优化结果优于其他算法，主要原因在于本文针对柔性工艺规划与车间调度集成优化问题设计了较好的编码方法与搜索策略，使得算法在求解效率及搜索能力上得到增强，因此验证了本文人工蜂群算法的有效性及优越性。本文算法求得的最优调度方案甘特图如图5所示。

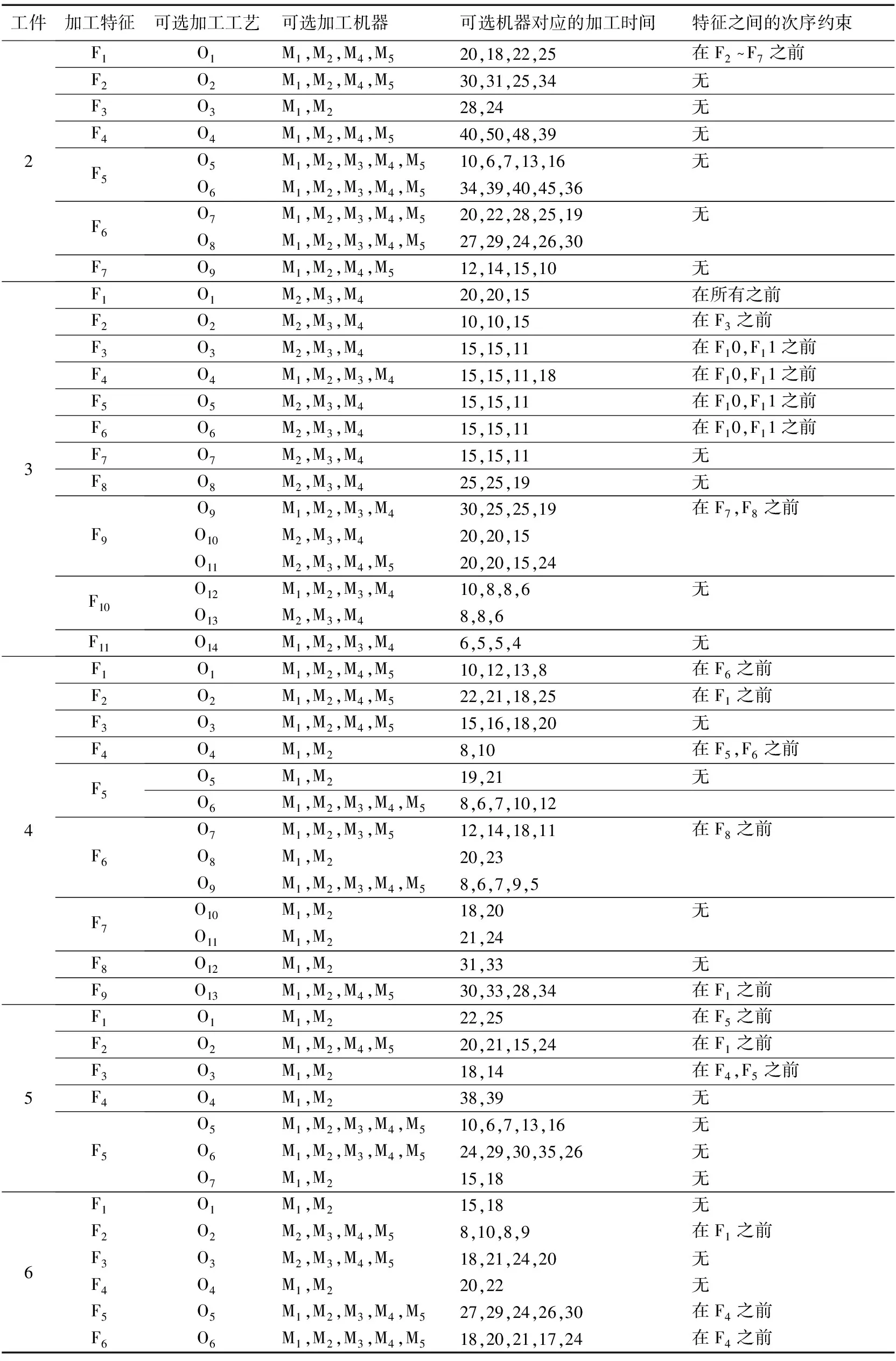
表2 工件的加工工艺信息表(测试1)

表3 工件在不同机器之间的转换时间(测试1)

表4 集成必要性验证测试结果(测试1)

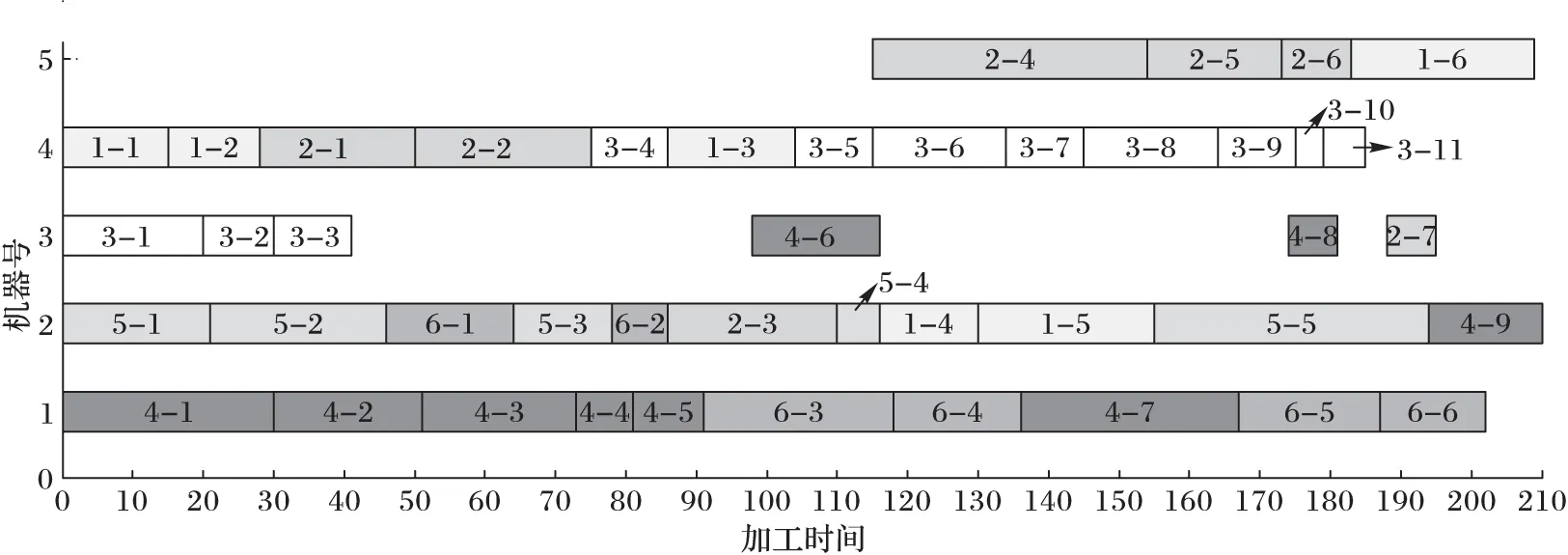
图4 集成式最优调度方案甘特图(测试1)

表5 工件的工艺信息[19](测试2)

Tab.5Processinformationofworkpieces(test2)

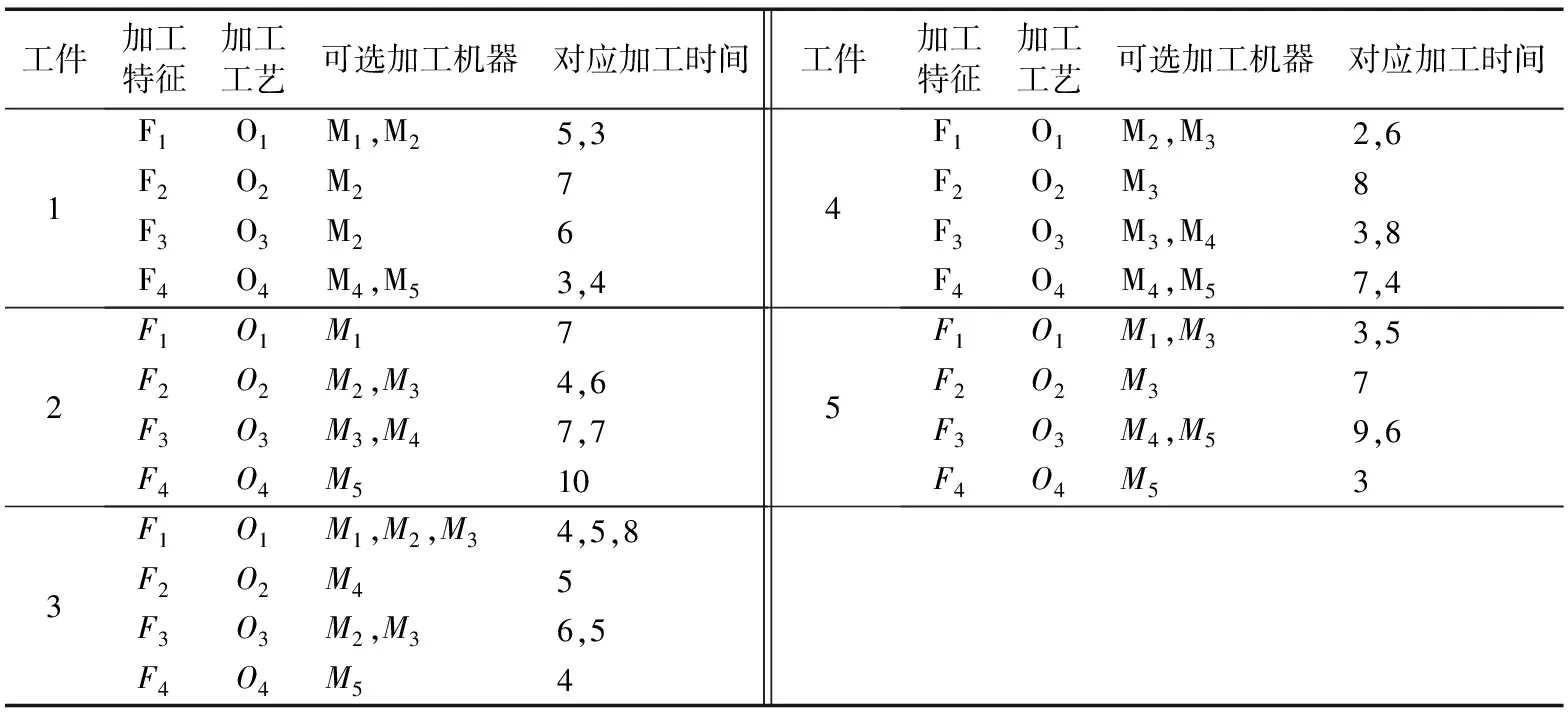
工件加工特征加工工艺可选加工机器对应加工时间工件加工特征加工工艺可选加工机器对应加工时间1F1O1M1，M25，3F2O2M27F3O3M26F4O4M4，M53，44F1O1M2，M32，6F2O2M38F3O3M3，M43，8F4O4M4，M57，42F1O1M17F2O2M2，M34，6F3O3M3，M47，7F4O4M5105F1O1M1，M33，5F2O2M37F3O3M4，M59，6F4O4M533F1O1M1，M2，M34，5，8F2O2M45F3O3M2，M36，5F4O4M54

图5 车间调度甘特图(makespan=31) (测试2)

表6 算法有效性验证测试结果(测试2)

Tab.6 Algorithm verification results (test 2)

方法makespan方法makespanHeuristic[19]38IGA[1]33SA[19]33ABC31Agent⁃based[20]33

5 结语

为了使制造车间能够及时响应订单的个性化需求，消除缺乏柔性的缺陷，提高其生产效率，本文提出一种基于交叉变异的人工蜂群算法对柔性工艺规划与车间调度集成进行优化求解，重点对算法的具体操作及工艺与调度集成优化流程进行了设计，最后选取最小化最大完工时间为优化目标，通过两部分实例对集成研究的必要性以及算法求解的有效性进行了验证。

References)

[1] 高亮，李新宇.工艺规划与车间调度集成研究现状及进展[J].中国机械工程，2011，22(8): 1001-1007.(GAO L, LI X Y.Current research on integrated process planning and scheduling [J].China Mechanical Engineering, 2011, 22(8): 1001-1007.)

[2] 宋栓军，杨佩莉,石雯丽.考虑多目标的柔性工艺与调度集成优化算法[J/OL].计算机应用研究，2017 [2016- 08- 05].http://www.arocmag.com/getarticle?aid=912497cbe6174f12.(SONG S J, YANG P L, SHI W L.Integrated optimization algorithm of flexible process planning and shop scheduling with consideration of multi-objectives [J/OL].Application Research of Computers, 2017 [2016- 08- 05].http://www.arocmag.com/getarticle?aid=912497cbe6174f12.

[3] 巴黎，李言，杨明顺，等.考虑不确定加工时间的工艺规划与调度集成问题研究[J].中国机械工程，2015，26(24):3348-3355.(BA L, LI Y, YANG M S, et al.Research on integrated process planning and scheduling problem with consideration of uncertain processing time [J].China Mechanical Engineering, 2015, 26(24): 3348-3355.)

[4] CHRYSSOLOURIS G, CHAN S, SUH N P.An integrated approach to process planning and scheduling [J].CIRP Annals — Manufacturing Technology, 1985, 34(1): 413- 417.

[5] BECKENDORFF U, KREUTZFELDT J.Reactive workshop scheduling based on alternative routings [C]// Proceedings of a Conference on Factory Automation and Information Management.Bocaraton, Florida: CRC Press, 1991: 875-885.

[6] 刘倩雯.人工蜂群算法及其在调度问题中的应用研究[D].北京: 北京交通大学，2014: 5-61.(LIU Q W.Research on artificial bee colony and its application in scheduling problems [D].Beijing: Beijing Jiaotong University, 2014: 5-61.)

[7] 瞿璨.面向绿色制造的工艺规划决策研究[D].武汉: 华中科技大学，2013:2-54.(QU C.Study on the process planning for green manufacturing [D].Wuhan: Huazhong University of Science and Technology, 2013: 2-54.)

[8] 吕盛坪，乔立红.工艺规划与车间调度及两者集成的研究现状和发展趋势[J].计算机集成制造系统，2014，20(2):290-300.(LYU S P, QIAO L H.Current status and developing trend of process planning and job shop scheduling [J].Computer Integrated Manufacturing Systems, 2014, 20(2): 290-300.)

[9] 吕盛坪，乔立红.工艺规划与车间调度复合式集成模型[J].计算机集成制造系统，2014，20(1):111-120.(LYU S P, QIAO L H.Hybrid integration model for process planning and scheduling [J].Computer Integrated Manufacturing Systems, 2014, 20(1): 111-120.)

[10] 崔晓康，肖艳秋，王磊,等.面向工艺规划与车间调度的集成方法研究[J].机床与液压，2015，43(3): 134-137.(CUI X K, XIAO Y Q, WANG L, et al.Research on integrated method of process planning and job-shop scheduling [J].Machine Tool & Hydraulics, 2015, 43(3): 134-137.)

[11] 王进峰，阴国富，雷前召，等.蚁群算法在工艺规划与车间调度集成优化中的应用[J].东南大学学报(自然科学版)，2012，42(S1): 173-177.(WANG J F, YIN G F, LEI Q Z, et al.Integrated process planning and scheduling based on an ant colony algorithm [J].Journal of Southeast Universit (Natural Science Edition), 2012, 42(S1): 173-177.)

[12] LIU Z, MA S, SHI Y, et al.Solving multi-objective flexible job shop scheduling with transportation constraints using a micro artificial bee colony algorithm [C]// Proceedings of the 2013 IEEE 17th International Conference on Computer Supported Cooperative Work in Design.Piscataway, NJ: IEEE, 2013: 427-432.

[13] 文笑雨.多目标集成式工艺规划与车间调度问题的求解方法研究[D].武汉:华中科技大学，2014: 5-61.(WEN X Y.Research on the solution methods for multi-objective integrated process planning and scheduling problem [D].Wuhan: Huazhong University of Science and Technology, 2014: 5-61.)

[14] 江铭炎，袁东风.人工蜂群算法及其应用[M].北京：科学出版,2014:16-264.(JIANG M Y, YUAN D F.Artificial Bee Colony Algorithm and Its Application [M].Beijing: Science Press, 2014: 16-264.)

[15] 吴正佳，罗月胜，周玉琼,等.一种求解典型JSP的改进离散粒子群优化算法[J].计算机应用研究，2013，30(8):2405-2409.(WU Z J, LUO Y S, ZHOU Y Q, et al.Improved discrete particle swarm optimization algorithm for typical Job-Shop scheduling problem [J].Application Research of Computers, 2013, 30(8): 2405-2409.)

[16] 张国辉，张凌杰，吴立辉,等.精英进化策略求解柔性作业车间调度问题[J].计算机应用研究，2016，33(12): 1-5.(ZHANG G H, ZHANG L J, WU L H, et al.Solving flexible Job-Shop scheduling with elite evolution strategy [J].Application Research of Computers, 2016, 33(12): 1-5.)

[17] 李新宇.工艺规划与车间调度集成问题的求解方法研究[D].武汉:华中科技大学，2009:58.(LI X Y.Research on the solution methods of integrated process planning and scheduling [D].Wuhan: Huazhong University of Science and Technology, 2009: 58.)[18] FANG H-L, ROSS P, CORNE D.A promising genetic algorithm approach to job-shop scheduling, re-scheduling and open-shop scheduling problems [C]// Proceedings of the 5th International Conference on Genetic Algorithms.San Mateo, CA: Morgan Kaufmann Publishers, 1993: 375-382.

[19] MORAD N, ZALZALA A M S.Genetic algorithms in integrated process planning and scheduling [J].Journal of Intelligent Manufacturing, 1999, 10(2): 169-179.

[20] FUJI N, INOUE R, UEDA K.Integration of process planning and scheduling using multi-Agent learning [C]// Proceedings of the 41st CIRP Conference on Manufacturing Systems.Berlin: Springer-Verlag, 2008: 297-300.

This work is partially supported by the Scientific Research Fund by Shaanxi Provincial Education Department (15JK1311), Research Start-up Fund for Doctor of Xi’an Polytechnic University (BS1301), Innovation Fund for Graduate Students of Xi’an Polytechnic University (CX201628).

SONG Shuanjun, born in 1974, Ph.D., associate professor.His research interests include optimization of production system, supply chain management.

YANG Peili, born in 1992, M.S.candidate.Her research interests include optimization of production system.

SHI Wenli, born in 1991, M.S.candidate.Her research interests include supply chain management.

Optimization of integrated flexible process planning and job shop scheduling based on artificial bee colony

SONG Shuanjun, YANG Peili*, SHI Wenli

(CollegeofMechanicalandElectricalEngineering,Xi’anPolytechnicUniversity,Xi’anShaanxi710048,China)

To achieve the optimization of integrated flexible process planning and job shop scheduling, taking the flexibility of manufacturing process and order and manufacturing machine of the workpieces into account, for minimizing the maximum completion time of the product processing task, an artificial bee colony algorithm based on crossover and mutation was proposed.Aiming at the discrete characteristics of integrated flexible process and job shop scheduling, the process route was coded in sequence, and the job scheduling was based on the working procedure.To improve the performance of the algorithm, by means of crossover and mutation operation of process population and scheduling population, the employed foragers and onlookers bees seeked local optimality, and the scouts seeked global optimality.On this basis, the necessity of the integration research and the effectiveness of the improved algorithm were verified by two test cases.

flexible process planning; job shop scheduling; Artificial Bee Colony (ABC)

2016- 07- 18;

2016- 08- 24。 基金项目:陕西省教育厅科研基金资助项目(15JK1311)；西安工程大学博士科研启动基金资助项目(BS1301)；西安工程大学研究生创新基金资助项目(CX201628)。

宋栓军(1974—)，男，陕西西安人，副教授，博士，主要研究方向：生产系统优化、供应链管理； 杨佩莉(1992—)，女，陕西兴平人，硕士研究生，主要研究方向：生产系统优化； 石雯丽(1991—)，女，甘肃陇南人，硕士研究生，主要研究方向：供应链管理。

1001- 9081(2017)02- 0523- 07

10.11772/j.issn.1001- 9081.2017.02.0523

TH166;TP

A