由一道高考题谈三角换元法

辽宁省铁岭县高级中学(112000)

杨宁宁●

由一道高考题谈三角换元法

辽宁省铁岭县高级中学(112000)

杨宁宁●

解决数学问题时，换个角度思考，往往会有意想不到的收获，甚至有时可以把复杂的问题简单化，换元法——三角换元，可以把陌生的问题转化为熟悉的问题，对具备某些条件的问题能起到事半功倍的效果.在保证换元前后变量范围一致的前提条件下，三角换元法在求最值，求某些函数值域，证明不等式问题上，可以化繁为简，优化解题过程.

三角换元；值域；不等式

一、求表达式最值

解 设x=2cosθ,y-1=2sinθ,0≤θ<2π,

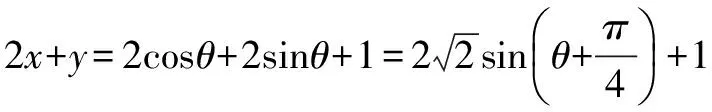
例2 在椭圆4x2+9y2=36上存在一点P,求点P到直线x+2y+36=0的距离最小值.

设x=3cosθ,y=2sinθ

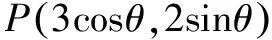
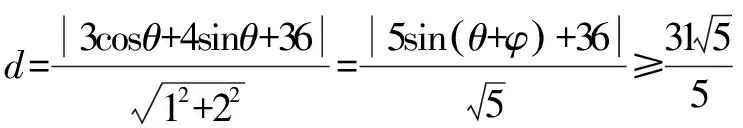
例3a,b为实数，a2-ab+b2=1,求a+b的最大值.

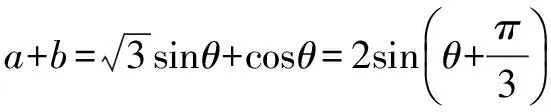
例4x,y∈R,4x2+y2+xy=1.求2x+y的最大值.

二、求函数值域

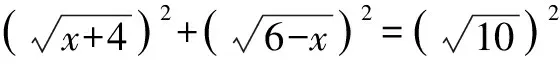
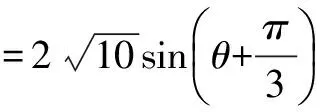
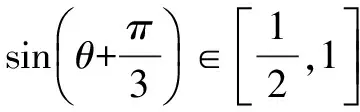
三、证明条件不等式

例6 设a2+b2=1,c2+d2=1.求证：ac+bd≤1.

证明 设a=sinθ,b=cosθ,c=sinφ,d=cosφ,

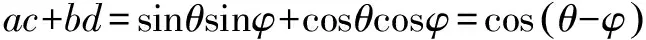
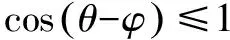
∴ac+bd≤1.

例7 设x2+y2≤1，求证：x2-y2+2xy≤2.

证明 设x=rcosθ,y=rsinθ(0≤r≤1).

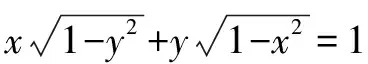
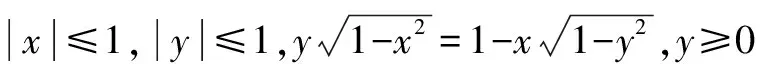
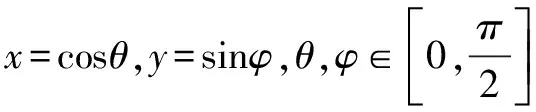
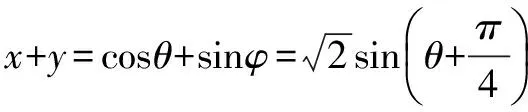
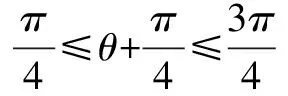
三角换元，关键是选择合适的换元对象，目的是变换研究对象，把复杂的问题简单化，在保证换元过程是等量代换的前提下，合理地把条件和结论联起来，甚至在解决数列，方程等问题中也有广泛的应用.

G632

B

1008-0333(2017)07-0024-01