一道有关二项式定理高考题的解法探究

江苏省常州市北郊高级中学(213000)

陈 鸾●

一道有关二项式定理高考题的解法探究

江苏省常州市北郊高级中学(213000)

陈 鸾●

2016年江苏高考数学的附加第24题

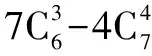
(2)设m,n∈N*，n≥m,求证：

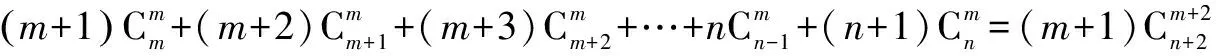
在去年高考的这道题中，笔者发现得分很低，对学生来说很难，但其实笔者研究下来，发现方法还是很多的，下面就分析出来的几种方法整理如下：

法一：也是标准答案的方法

当n=m时，结论显然成立.当n>m时,

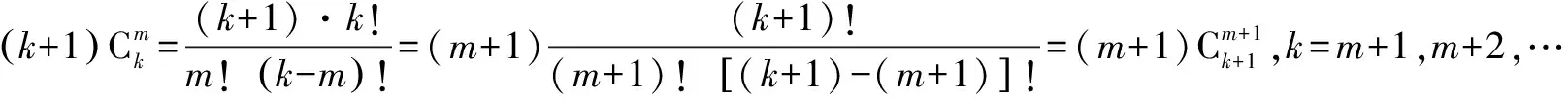
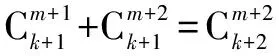
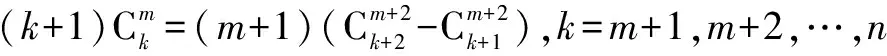
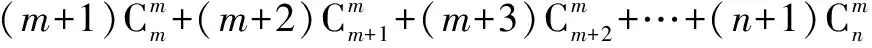
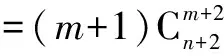
这种方法过程很简洁，但是公式运用要非常熟练，学生不太容易想到.

法二：构造函数F(x)

F(x)=(m+1)(1+x)m+(m+2)(1+x)m+1+(m+3)(1+x)m+2+…+(n+1)(1+x)n①.

要求的式子的左边即为F(x)的xm项前的系数,

再对函数进行等差比求和的化简，得

(1+x)F(x)=(m+1)(1+x)m+1+(m+2)(1+x)m+2+…+n(1+x)n+(n+1)(1+x)n+1②

①-②：

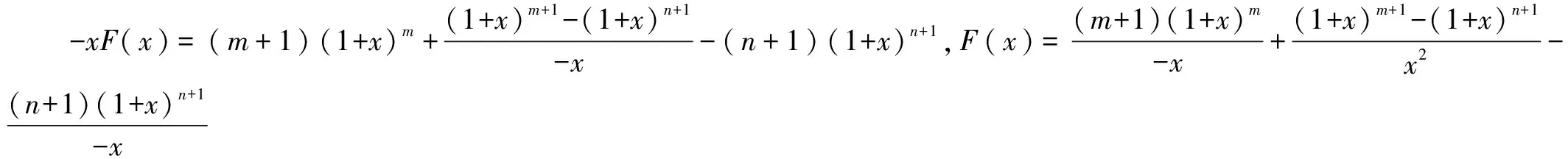
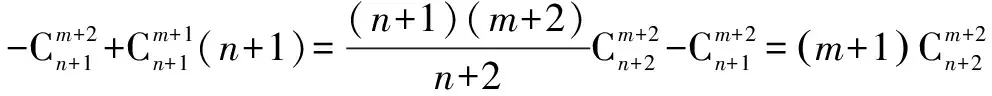
评析 在进行构造函数时，发现还可以构造h(x)=(1+x)m+1+(1+x)m+2+…+(1+x)n+1.

求导之后就是上面构造的F(x)，但是计算相对较简单，不需要等差等比数列求和.

这种方法学生比较能够想到，但是过程中计算也是很大的.

法三：利用拆补一轮又一轮进行计算

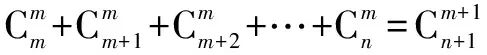
原式

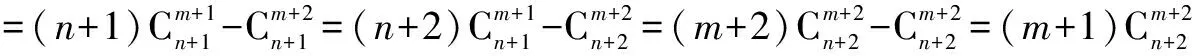
这种方法也是很不错的.

G632

B

1008-0333(2017)07-0026-01