小组合作学习中关于学习内容选择的几点思考

浙江省温岭市泽国二中 黄丹萍

小组合作学习中关于学习内容选择的几点思考

浙江省温岭市泽国二中 黄丹萍

小组合作学习能给学生自主、合作的机会，既能培养学生的团体合作意识，发展学生的交往能力，又能培养学生的竞争意识和个人责任感，提高了学习效率，培养学生良好的学习习惯和团体意识。选择具有合作价值的学习内容是开展小组合作学习的重要前提。

小组合作；学习内容；积极参与

自主、合作、探究是新课改倡导的三大学习方式。新课改明确要求学生是课堂的主体，是学习的主人，在课堂教学中，应让学生主动参与到学习过程、实践过程中来，要把课堂充分地交还给学生，而教师要当好课堂教学的组织者、学生学习的引导者和合作者的角色。小组合作学习恰好能给学生自主、合作的机会，既能培养学生的团体合作意识，发展学生的交往能力，又能培养学生的竞争意识和个人责任感。小组合作学习的目的是提高学习效率，培养学生良好的学习习惯和团体意识，而是否能达到学习目标的要求取决于小组合作是否有效，也只有有效的小组合作，才能使课堂达到高效。教师作为课堂的组织者和引导者，必须先对学习内容进行充分理解，对症下药，克服小组合作学习的弊端，让每位学生能积极地参与到小组讨论中来，使小组合作学习不会流于形式，而是实实在在地体现出它的优势。要开展有效的小组合作学习，就需要选择恰当的任务和时机，不是所有内容都需要进行小组讨论的，选择具有合作价值的学习内容是开展小组合作学习的重要前提，笔者针对这一方面进行了以下几点思考归纳：

一、一题多拓型

一题多拓意在以旧带新，既避免题海战术给学生带来的烦闷，又可在遇到新问题时萌发创新灵感。教师在教学过程中，可引导各小组去探求“变异”的结果，培养学生的发散性思维，激发小组成员的创造精神，发展他们的创新思维。

例如：在△ABC 中，AB=3厘米，BC=4厘米，B=90°，点P从点A开始沿AB边向点B以1厘米/秒的速度移动，点Q从点B开始沿BC边向点C以2厘米/秒的速度移动，如果P，Q分别从A，B同时出发，几秒后△PBQ的面积等于8平方厘米？

变式一：原题中的题设条件不变，求解下题：

如果P、Q分别从A、B同时出发，并且P到B后继续在BC边上前进，Q到C点后又继续在CA边上前进，经过几秒钟，能使△PCQ的面积等于12.6平方厘米？

变式二：将原题中题设条件变为：以B点为原点，AB所在直线为x轴，建立平面直角坐标系，其余条件不变，求解下列各题：

（1）求当∠BPQ=45°时，PQ所在直线的解析式；

（2）AC所在直线与PQ所在直线可能平行吗？若平行，运动到何时平行？

通过一题多拓对小组成员进行训练，使学生掌握变式题与原题的内在联系以及本质，达到一把钥匙开几把锁的效果，这不仅能培养学生善于发现问题、分析问题和解决问题的能力，而且能训练学生的创新思维，发展他们的思维空间，开发学生的创造力。

二、类比猜想型

众所周知，数学知识本身具有抽象性、复杂性。教师在教学中若能引导学生进行观察、类比，对问题产生猜想，则能减少掌握抽象知识的困难，化抽象为直观，化复杂为简单，化未知为已知，从而激发学生的学习兴趣。类比和归纳这两种合情推理方法与学生的学习生活和社会生活的联系比较紧密，以此作为改变“重结果，轻过程；重结论，轻发现；重知识，轻能力”的弊端、培养学生创造和发现能力的入口，具有较强的操作性。产生疑难，猜想辨析，能促进学生积极思维，激发学习的积极性。在教学过程中向学生提出新颖、巧妙的问题，使学生头脑里产生疑问，造成学生“心求通而未能得、口欲言而不能说”的情势，从而唤起学生强烈的求知欲，使他们积极踊跃地投入到小组讨论中去。

例如：在学习《一元一次不等式》时，通过类比等式性质的探究方法，思考：

用“＜”或“＞”填空，并总结其中的规律：

（1）5＞3，5+2 ______ 3+2，5-2_______ 3-2;

（2）-1＜3，-1+2______ 3+2，-1-3_______ 3-3;

（3）6＞2，6×5_______ 2×5，6×(-5)______ 2×(-5)；

（4）-2＜3，(-2)×6______ 3×6，(-2) ×(-6)______ 3×(-6)。

类比等式的两条性质，有些同学会得出不等式的两条性质，但也有些同学会有疑问：不等式的性质和等式的性质完全一样吗？显然，根据我们的计算可以发现，当两边同时乘以一个负数时，不等号的方向是要改变的。因此，这里既经历了类比归纳，又需要进行新的猜想判定，得出新的性质。

通过类比猜想，小组成员的质疑、释疑最后总结归纳，既调动了学生学习的积极性，活跃了课堂气氛，加深了记忆，又培养了学生的能力。这比教师马上给出定理性质，然后由学生去硬记要强得多。

三、设疑质疑型

常有疑问，才能有思考。在数学教学中，要鼓励学生设疑、释疑，能对所观察的对象大胆提出疑问，通过组内讨论，组间辩论，细心探索、创立新举。

例如：在教学反比例函数的性质时：已知y关于x成反比例函数，当x=-1时，y=4；当x=2时，y=-2，求这个反比例函数关系式，并说明这个反比例函数的增减性。

有的学生求出解析式后得k=-4＜0，故y随x的增大而增大，但也有学生当即提出疑问，由已知条件中的数据显示，显然是y随x的增大而减小的。于是反比例函数增减性的问题就成了一个疑点，它将学生的思维过程毫无拘束地暴露，调动了小组成员积极参与思维活动，积极讨论中来。小组成员通过设疑、释疑，使得学生对反比例函数的性质有了完整、深刻的理解。在小组学习中，要引导小组成员善于提出问题，进而提出问题的解决方法；引导小组成员把有待解决的问题，通过某种转化过程归结到比较容易解决的问题中去。数学课堂要为学生提供“做”数学的机会，使学生在具体的操作、整理、分析和探索交流活动中，变抽象为具体，获得广泛的活动经验，从而实现有效学习。

四、开放探究型

开放性习题是相对于常规问题而言的，常规问题的条件和结论已由题目给出，是确定的、完备的，学生解答时目标明确，解题模式一般都是固定的，但思维方式有一定的局限性。而开放性习题由其特点所致，学生需要通过观察、比较、分析、综合甚至猜想，展开发散性思维，需要小组成员运用已学过的数学知识和数学方法，经过必要的推理才能得出结论。

例如：某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料生产A，B两种产品共50件，已知生产一件A种产品需甲种原料9千克、乙种原料3千克，可获利700元；生产一件B产品需用甲种原料4千克、乙种原料10千克，可获利1200元。

（1）按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来；

（2）设生产A、B两种产品获总利润为y元，其中一种产品生产件数为x件，试写出y与x的函数关系式，并利用函数性质说明（1）中哪种方案获利最大？最大利润是多少？

这是一道具有实际应用意义的开放题。安排生产方案往往用不等式解确定考虑范围，解答（2）中的函数虽是一次函数，但其符合题目实际意义的自变量x的范围只是三个孤立的点，这种情况在实际问题中大量存在。这一类题，小组讨论过程突出了思维的多样性，调动了学生积极、主动参与学习的兴趣，不知不觉地把“强制性”的枯燥教学活动变成了“自觉性”的趣味横生的小组活动，激发了学生学习数学的兴趣。

加强数学课外活动的指导，创设和优化数学教学环境，是实施本课题的有效途径。小组合作教学模式充分体现了以教师为主导，学生为主体的教学原则，有利于建立新型的师生关系，有利于调动和发挥学生学习的积极性，提高数学学习效率。

[1]陈艳飞．浅谈初中数学教学中的小组合作学习[J]．教育科学学刊，2015．

[2]甘迎平．浅谈初中数学课堂教学的有效性[J]．新课程·中学，2014（3）．图形则又有所变化，如下图所示：

除了正弦函数之外，三角函数中还包含了余弦函数、正切函数等等，我们学完基本的三角函数图象和性质之后，通过大量的练习进行综合考察。根据学习经验，我们在做三角函数的练习时通过水波变化演示图象可以更好地解题。

二、三角函数例题中的水波变化演示

三角函数在高考中占有一定比例，我们在做题的过程当中，利用数形结合的思想，以图象的形式可以更快更准确地解题。

1．三角函数的对称性呈现

例1 设函数f(x)的图象与直线x=a，x=b及x轴所围成图形的面积称为函数f(x)在[a，b]上的面积。已知函数y=sinnx在上的面积为，求y=sin(3x-π)+1在上的面积。

根据这道题的已知条件，通过画图的方式进行解答，首先作函数y=sin(3x-π)+1在上的图象，如图1所示：

图1

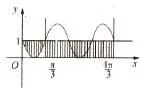
图2

2．三角函数的周期性呈现

（1）求w的值及函数f（x）的值域；

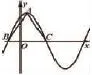
图3

这道题考查了三角函数诱导公式以及图象变换等的知识。我们必须通过图象并对题目给出的已知条件进行分析，对于较为复杂的三角函数的性质，一般情况下先要将复杂的三角函数转化为我们已知和熟悉的形式：y=Asin（wx+ψ），用正弦函数y=Asin（wx+ψ）（w＞0，，x∈R）呈现图象，在定义域范围内先确定图象的最高点和最低点，求出半个周期，再画出图象。在解较为复杂的三角函数时，利用数形结合的思想，依据三角函数的图象以及水波变化演示呈现出的特征，求出w的值及函数f（x）的值域。

3．三角函数水波变化演示取值范围

在三角函数当中，水波变化演示对帮助解不同类的题目有很大的好处，比如求三角函数的最值问题、求取值范围等等，以下则是水波变化演示求取值范围的具体例子。

图4

总而言之，水波变化演示实际上就是以图象的形式呈现三角函数，图象则可以更为形象直观地表现三角函数的性质，如三角函数的值域、定义域、周期等，并由此可以帮助我们更好地理解三角函数，帮助我们更好地解题。在一些看似很难并且复杂的三角函数题目中，通过水波变化演示就能很快呈现出一些必要的条件，最终可以更简单地呈现答案。在学习三角函数的过程中，我们也能更好地理解关于函数的许多公式，从而更快记下公式并运用到练习当中，降低了我们学习三角函数的难度。本文主要通过三角函数图象的变换以及例题，分析水波变化演示与三角函数的特征，其中还有不全面和不完善的地方，还请广大教师批评指正。

【参考文献】

[1]赖彩玲．论高中数学中的三角函数变换[J]．教育教学论坛，2012（12）：116-117．

[2]杨平荣．对数形结合思想在初中函数教学中的作用探讨[J]．学周刊，2013（22）：144-145．

[3]杨浩云．利用数形结合探讨三角函数的周期性[J]．赤子(中旬)，2014（01）：273-274．

[4]覃桂燕．几何画板在三角函数教学中的应用[J]．广西教育学院学报，2011（01）：174-178．

[5]王洁．高考三角函数题型探析[J]．甘肃联合大学学报(自然科学版)，2012（S4）：50-52+54．

[6]孙旭东．2013年高考“三角函数”专题分析[J]．中国数学教育，2013（Z4）：29-31+54．

[7]张建禄．六种求三角函数最值的思维方法[J]．科教导刊(上旬刊)，2014（02）：185-186．