勾股数及其活动课教学研究
2017-04-14江苏省扬州市竹西中学225000
江苏省扬州市竹西中学(225000)
宋 扬●
勾股数及其活动课教学研究
江苏省扬州市竹西中学(225000)
宋 扬●
勾股定理是数学的一个很重要的定理,在人类的文明史中有着杰出的贡献,由勾股定理引出的“勾股数”也因此崭露头角,继而声名远扬.本文在文【1】的基础上作了修改、补充和拓展,并运用到数学综合与实践的教学活动中,引发了同学们极大的兴趣,取得了令人满意的教学效果.现将活动课的内容和教学要点展示如下,主要是阐明了勾股数的三种计算公式的由来、产生过程及其内在联系,用几种不同的方法探寻勾股数的规律,并形成各种各样的勾股数表达式.同时,明确回答了文【1】和文【2】中相关内容提出的疑难问题,而且有所增强,从理论上和活动课教学实践上都作了较为充分的研究.
数学活动课;勾股数;勾股数计算公式;勾股数表达式;勾股数的性质;活动创新
一、课题:探寻勾股数的规律
二、事前准备:
1.自备计算器一台.
2.熟悉勾股数的基本概念.
3.了解并初步掌握古代数学家给出的勾股数计算公式.
三、活动内容和实施过程
1.从任一大于1的奇数出发,寻求一组勾股数中的另两个数
设a为大于1的奇数,(a,b,c)为一组勾股数,填表:

表1
(1)在表1中,b和c之间的数量关系是____;b、c与a2之间的关系式是____.根据以上规律,写出勾股数(19,____,____);(75,____,____).
(2)一般地,从a=2n+1(n∈Z+)出发,请你推导出计算勾股数的一组公式.
2.从任一大于2的偶数出发,寻求一组勾股数中的另两个数
设a为大于2的偶数,(a,b,c)为一组勾股数,填表:
(1)在表2中,b和c之间的数量关系是____;b、c与a2之间的关系式是____.根据以上规律,写出勾股数(18,____,____);(40,____,____).
(2)一般地,从a=2n(n∈Z+,n>1) 出发,请你推导出计算勾股数的一组公式.
3.尝试从乘法公式入手探索构造勾股数的方法
构造勾股数,就是要寻找三个正整数,使它们满足( )2+( )2=( )2的形式.
(1)联想到乘法公式,显然有(x-y)2+4xy=(x+y)2,从这个恒等式出发,请你推导出计算勾股数的一组公式.
提示:为了使等式左边的4xy也能写成( )2的形式,可令x=m2,y=n2(m,n∈Z+,且m>n).
(2)根据上述探索得到的勾股数表达式,构建下列表格,并填写勾股数,你一定能有所发现.

表3

mnm2-n22mnm2+n2213141516171
(3)观察勾股数:3,4,5;…;16,63,65;20,99,101;…(*)这里的每组勾股数中都有两个数是连续的奇数,你能借助3.(1)中推导出的勾股数计算公式,探索并构造这样的勾股数吗?请试一试.
提示:可先构建下列表格并填写,然后推导出与(*)相应的勾股数表达式(计算公式).
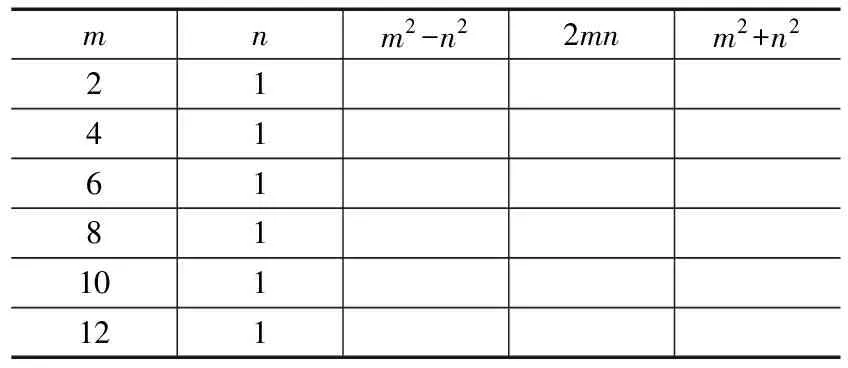
表5

表6
四、活动创新素材
1.探讨勾股数的三种计算公式之间的内在联系
(1)毕达哥拉斯给出的计算公式:
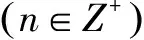
(2)古希腊哲学家柏拉图给出的计算公式:
n2-1,2n,n2+1.(n∈Z+,n>1)②
(3)古希腊数学家丢番图给出的计算公式:
m2-n2,2mn,m2+n2.(m,n∈Z+,m>n)③
2.一位数学家在他找到的勾股数表达式中,用2n2+2n+1(n∈Z+)表示勾股数中最大的一个数,请你找出另两个数的表达式.
3.如果用2n2+2n+1(n∈Z+)表示勾股数(表达式)中最小的一个数,你能找出另外两个数的表达式吗?
4.观察勾股数6,8,10;10,24,26;…;22,120,122;26,168,170;… 这里的每组勾股数中都有两个数是连续的偶数,你能借助1.③探索并求出相应的勾股数表达式吗?
5.设 2n(n∈Z+,n≥2)是勾股数组中的一个数,但不是最大的一个,试寻求勾股数组中的另两个数.
(1)当n=2,3,4,5,6时,请分别求出含有2n的所有勾股数组;
(2)当n=k时,含有2k的全部勾股数组有什么规律?
6.如图1,已知四边形ABCD是长方形,AC为对角线.

图1 图2
如图2,ABCD-A1B1C1D1是长方体.图1中的线段AB、BC、AC分别对应图2中的面ABB1A1、面BCC1B1、面ACC1A1.设这三个面的面积分别为α、β、γ,试问α、β、γ是否满足勾股定理?为什么?α、β、γ是不是一组勾股数?又为什么?
7.是否存在这样的3个非零的整数a、b、c,使得a3+b3=c3成立?你能进行一番探索吗?试一试.
五、部分答案或析解
活动1.(1)c=b+1;b+c=a2;180,181;2812,2813.
(2)解法一:a=2n+1,根据(1)中的两个关系式,有2b+1=a2=(2n+1)2,得b=2n2+2n,c=2n2+2n+1.
解法二:由c=b+1和勾股数定义,有(2n+1)2+b2=(b+1)2,
得b=2n2+2n,c=2n2+2n+1.

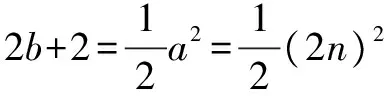


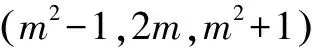
(3)从填表结果可以看到,表5和表6实际上是完全相同的,这说明勾股数表达式

也可由直接进行理论推导而得到:设勾股数中两个连续的奇数为2m-1和2m+1,则显然有(2m+1)2-(2m-1)2=8m,令m=2n2,有(4n2+1)2-(4n2-1)2=(4n)2,故所求勾股数表达式(计算公式)为(4n2-1,4n,4n2+1)(n∈Z+).
活动创新1.①是③当m=n+1时的特殊情形.用集合的观点看,把每一组勾股数看作一个元素,则由①表示的集合是由③表示的集合的子集.类似地,②也是③的特殊情形,集合②也是集合③的子集.
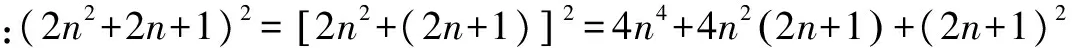

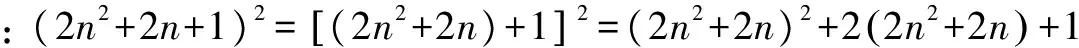

即(2n+1)2+(2n2+2n)2=(2n2+2n+1)2.故所求为2n+1和2n2+2n.


(1)当n=2时,求得1组勾股数:(4,3,5).
当n=3时,求得2组勾股数:(8,17,15),(8,10,6).
当n=4时,求得3组勾股数:(16,65,63),(16,34,30),(16,20,12).
当n=5时,求得4组勾股数:(32,257,255),(32,130,126),(32,68,60),(32,40,24).
当n=6时,求得5组勾股数:(64,1025,1023),(64,1014,1010),(64,260,252),(64,136,120),(64,80,48).
(2)当n=k时,可求得k-1组含有2k的勾股数.能否写出一般的勾股数表达式?留作练习.
当2n为勾股数组中最大的一个数时,能否求出另外两个数?也留作练习.
6.α、β、γ满足勾股定理.证:设AB=a,BC=b,AC=c,BB1=h,则可推得α2+β2=γ2.但α,β,γ不一定是勾股数,因为α,β,γ未必都是整数.
7.先了解一下著名的费马最后定理:“对于任何自然数n(n>2),方程xn+yn=zn关于x,y,z无正整数解”.根据费马最后定理,方程x3+y3=z3没有正整数解.以下分三种情形讨论:
(ⅰ)当a、b都为正整数时,由关系式a3+b3=c3知,c也为正整数,这与费马最后定理相矛盾.
(ⅱ)当a、b都为负整数时,由关系式知,c必为负整数.设a=-u,b=-v,c=-w,则有 (-u)3+(-v)3=(-w)3,从而有u3+v3=w3(其中u、v、w都是正整数),这也与费马最后定理相矛盾.
(ⅲ)当a、b中有一个为负整数时,不妨设a为正整数,b为负整数,设b=-v,则有a3+(-v)3=c3,若a>v,则c>0,从而有c3+v3=a3(其中c、v、a都是正整数),这仍然与费马最后定理相矛盾;若a 综上所述,不存在这样的非零整数a、b、c,使得a3+b3=c3成立. 1.勾股数的定义 定义1.直角三角形三条边的长a、b、c如果都是整数,则称a,b,c为一组勾股数. 定义2.满足关系式a2+b2=c2的3个正整数a,b,c称为一组勾股数,记为(a,b,c).例如(3,4,5)就是一组最简单的勾股数. 定义3.方程x2+y2=z2的任一正整数解(a,b,c),称为一组勾股数. 显然,上述三个定义是等价的. 2.勾股数的性质 (1)勾股数中的三个数不可能全是奇数. (2)勾股数中的三个数只有下列两种类型:要么三个全是偶数,要么只有一个偶数. 思路点睛:根据定义2,等式两边必须同为奇数或同为偶数,即可证得. (3)满足关系式a2-b2=c2的3个正整数a,b,c,是一组勾股数. (4)若(a,b,c)是勾股数,则(ka,kb,kc)(k∈Z+)也是勾股数. (5)勾股数有无数组. (6)对大于2的任何一个整数,都可以找到至少一组勾股数. (7)如果一组勾股数中两个较大的数相差1,那么这两个数的和就是第三个数的平方. (8)如果两个较大的数相差2,那么这两个数中间所夹的整数是第三个数的一半的平方. (9)任一勾股数表达式都不能覆盖所有的勾股数.例如,勾股数表达式 (m2-n2,2mn,m2+n2)(m,n∈Z+且m>n)尽管可表示无数组勾股数,但不能表示所有的勾股数,比如,勾股数(9,12,15)就不能由该表达式算出. 1.认真筹划好活动课事前准备工作.可提前3~5天印发活动课预习单,明确预习要求,让全班每个同学都有所准备. 2.预习单上的主要内容有(1)勾股数的概念:定义和几个有趣的性质;(2)古代数学家给出的计算勾股数的三个公式,要求学生根据勾股数定义分别加以验证;(3)活动1和活动2的内容,包括观察表中数字的规律、填表、填空等.这样,可为活动课大容量教学赢得许多时间. 3.充分发挥数学兴趣小组的助手、先行和引领作用.兴趣小组成员可适当分工,每2~3人领一个专题(比如,对勾股数某个性质的论证)或一项活动内容,各自做好重点准备,以确保活动课顺畅进行. 4.利用板报、墙报或数学之窗(数学角),分阶段公布活动课相关内容,紧密配合活动课的开展. 5.教学方式主要是引导、探究式.采用顶层设计、分项实施,逐步引导、共同探究,举一反三、层层递进,最终到达目标.老师指点少而精,及时、准确到位,并运用好多媒体教学手段,及时展现当前所要解决的问题、解决的过程和结果.让同学们自主探究、分组讨论的时间既紧凑又充分. 6.对具体的勾股数,让同学们适时使用计算器进行演算,帮助探寻规律,以节省时间. 7.与本次活动课链接的课本基础知识有:勾股定理、代数式、乘法公式、恒等变形、方程(组)、不定方程及正整数解、集合、简单的推理论证等. 8.活动创新素材的收集、整理待课后完成.可发动全班同学每人收集1~2项,经汇总、整理、去重、甄别、修订后,印发补充讲义,实现成果共享,扩大教学效应. 实践又一次表明,数学活动课的教学丰富多彩、成效显著,探究性学习越来越展现出强大的生命力.数学新课标已经为我们照亮了胜利前进的航程,乘风破浪、勇敢向前,就一定能够到达理想的境界. [1]《数学综合与实践活动》编写组. 勾股数的探索,数学综合与实践活动(八年级上册).南京:江苏科学技术出版社,2010. [2]杨裕前,董林伟.勾股定理,数学教师教学用书(八年级上册).南京:江苏凤凰科学技术出版社,2016. G632 B 1008-0333(2017)08-0002-03六、勾股数的基本概念

七、本次活动课教学要领
