巧解有理数运算

江西省赣州市安远县鹤子初级中学(342100)

魏煌胜●

巧解有理数运算

江西省赣州市安远县鹤子初级中学(342100)

魏煌胜●

本文根据笔者根据多年的教学经验，对初中数学有理数相关的几种常见解题技巧进行了归纳.

有理数运算；解题技巧；观察

一、 “化零为整”法

例1 计算：99+999+9999+102+1002+10002.

分析：通过观察可以发现，上式中的每个数都与其相邻的整数很接近，如99与100相差1,…, 9999与10000相差1；而102比100多2，…，10002比10000多2.因此可以凑成整百、整千、整万……的方式来快速求解.

解 原式=(100-1)+(1000-1)+(10000-1)+(100+2)+(1000+2)+(10000+2)=(100+1000+10000+100+1000+10000)+(2+2+2-1-1-1)=22200+3=22203.

“化零为整”法是将一个算式中能够近似为整数的部分凑整后，进行计算.目的是简化计算步骤，利用口算来解决复杂有理数的运算.其难点是在“化零为整”的过程中，用来凑整的简单整数的个数和加减关系注意不要混淆.

二、“化整为零”法

分析：上式是一个整数与分数相乘的过程，一般我们先考虑约分，但观察发现，原式无法约分.我们通过将整数部分根据分数的分母“化整为零”，将99转化为(98+1)，97转化为(98-1)，转变为可约分的数来进行计算.

“化整为零”法一般应对整数与分数相乘的习题，将整数部分“化整为零”，拆解为与分数部分可以约分的俩部分来计算.难点是计算过程中要注意分析整数和分数的关系，“化整为零”要恰如其分.

三、结合法

例3 计算：1-2+4-6+8-10+12-…-98+100.

分析 对于上式这类习题，直接计算肯定非常复杂，考察的目的就在于对简便算法的掌握.通过观察发现，从1到100，依次加减的过程，可转化为1+(-2)+4+(-6)+8…，那么从第二个数开始，相邻俩个数的和为-2，可将和为-2的组进行归纳，快速计算出结果.

解 原式=1+(-2+4)+(-6+8)+…+(-98+100)=1+(-2)× 25=-49.

结合法所涉及的题目一般如例3所示，题目较长，这就暗示着题目有一定的规律性.其实结合法就是将题目中有规律部分总结归纳的过程.其难点在于规律的发掘和重叠个数的计算.

四、公式法

例4 计算：

分析 当我们遇到较为复杂的有理数的混合运算时，应首先想到对公式的运用.有理数的混合运算，我们首先应找到公因子，如本题提出公因子0.3和1.2；其次转变运算符号，将÷转变为×；最后运用分配律进行计算.

公式法解决有理数的混合运算，除了考察对题目的转化能力外，还需掌握分配律、结合律、除法的性质这类基本的运算法则.此类题难点在于针对所运用公式，进行试题的转化过程.

五、替换法

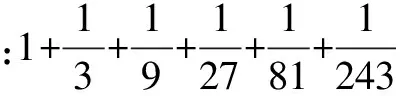
分析 观察发现，上式的后一项是前一项的三分之一，单纯的通分计算繁琐且易错，则考虑用替换的方式来解题.

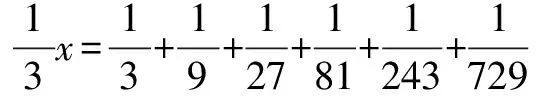
这类题目的规律很明显，题目的各个部分存在是重复或比例关系，用替换法解决这类题目，大大减少运算的步骤和出错的可能.此类题的难点在于识别题目的内在规律并成功替换转化.

六、添项法

例6 计算(1+2)(1+22)(1+24)(1+28).

分析：因为题目涉及平方，通过观察，我们发现题目与平方差公式相似，但缺少项目.所以我们可以进行添项，因为1=2-1，恰能和(2+1)进行组合.

解 因为1=2-1，所以，原式=(2-1)(2+1)(1+22)(1+24)(1+28)=(22-1)(22+1)(1+24)(1+28)=(24-1)(24+1)(1+28)=(28-1)(28+1)=216-1.

添项法的目的在于可以使复杂题目转化成有规律可循的题型，这样有利于快速准确的计算.掌握这个方法的难点在于发掘题目可能遵循的内在规律，设计简便合理的添项.

总之，有理数的运算虽然变化方式多，但百变不离其中.针对每种方法的难点，最有效的解决方式就是通过习题来强化方法的运用.今后若教师能在教学中归纳和引入恰当的解题技巧，学生在学习可以自主的分析题目规律、懂得活学活用.那么师生定能够在有理数运算中各有所获.我们也希望今后的教研和学习中，老师和学生相辅相成，设计更加灵活多变的方法，共克难题.

[1]易思源.有理数计算的常用方法[J]. 初中数学教与学，2011(06)

[2]丁式清.有理数的运算技巧归纳[J]. 数学学习与研究，2014(12)

G632

B

1008-0333(2017)08-0036-01