基于AHP和Floyd算法的农产品物流中心选址研究

赵晏林，李 琴，文忠波,周真丙

(攀枝花学院，四川 攀枝花 617000)

基于AHP和Floyd算法的农产品物流中心选址研究

赵晏林，李 琴，文忠波,周真丙

(攀枝花学院，四川 攀枝花 617000)

以农产品物流中心的选址为研究对象，对国内外农产品物流现状分析的基础上，结合农产品特性，以攀枝花农产品物流为例，构建农产品二级物流节点到枢纽中心的物流网络.基于AHP和Floyd算法，充分分析攀枝花农产品的产地分布情况，考虑影响农产品物流中心选址的主要因素，对农产品物流节点和枢纽中心进行选址研究，设计出最适合攀枝花农产品物流的选址方案，以期解决攀枝花农产品物流成本高、产品损耗大、运输周期长等长期困扰当地农业经济发展的问题.

农产品物流；物流中心；选址；AHP；Floyd算法

生活质量的提高意味着人们对农产品的需求不断增加，对农产品的运输配送有更高的要求.而相较于农业的不断发展，农产品物流方面却存在着较多问题，例如路途运输的时间长，运输成本高，运输过程中农产品的损耗较大、鲜活度降低等.我国水果、蔬菜在物流中的损失率为 25%-30%，国际标准为 5%，而农产品物流业最发达的美国仅为 1%-2%[1-2].物流配送成本占物流总成本的 35%-60%，占商品价格的 4%-10%，而对于农产品物流，这个比例更大，配送费用极大地影响农产品物流企业的经济效益[3].效率低、成本高、流通困难等问题已经成为阻碍我国农业经济发展的关键因素.

物流中心的建设可以提高农产品的物流效率，降低农产品物流成本，减少农产品流通不畅导致的高损耗，促进生产和消费之间的协调与配合，保证物流系统的平衡发展.农产品物流中心的选址是发展农产品物流的基础环节，也是最为重要的环节.物流中心一旦选定将长时间运营，其选址不仅与运行费用直接相关，而且会对工作效率及物流控制水平产生很大影响.此外，物流中心的功能、形态等也会受到地区因素的影响.陈超等对我国城镇化背景下农产品物流发展的现状与对策进行分析，指出了我国农产品物流基础设施薄弱、物流成本高、物流主体发展不完善等问题[4].索志林等对农产品物流中心选址模型的构建和应用进行研究，提出了以物流成本最小为目标的选址优化模型，并采用混合整数规划法对选址模型进行了求解[5].许金立从供应链战略协同角度研究农产品物流运行机制，以建立战略联盟，实现最佳的农产品物流运行[6].总体来看，我国对农产品物流的研究主要集中在政策方针、网络构建和运行管理等方面，对农产品物流中心的选址研究却不够深入.

1 攀枝花农产品生产现状

攀枝花市地处南亚热带，该区域光照充分.近年来，攀枝花市政府充分发挥区域优势，大力发展特色农业，全力打造有地方特色和优势的农产业.以水果为主的农产品，特别是芒果、枇杷、火龙果等在攀枝花大面积种植，每年产出量都很大.其主要产地为仁和区、盐边县和米易县，东区和西区也有少量生产.目前为止，攀枝花市已经初步建成13个品种包括40 多个特色农产品的生产基地，形成了优质粮食基地、特色水果基地、早市蔬菜基地、无公害养殖基地和优质烤烟基地五大主要特色农产品基地.此外，食用菌、蚕桑、花卉、生物药业等特色农产品基地也逐步成为攀枝花市新的亮点.

根据攀枝花市4个区域的农产品生产地分布情况，需要建立3个农产品物流中心为这4个区域的农产品产地服务.经过综合考虑，结合其他选址原则和影响因素，5个可作为备选的地点为格里坪镇、总发乡、红格镇、银江镇和大田镇，可分别设为C1、C2、C3、C4、C5.计划从中选择3个地点作为农产品物流中心建设点，为周边农产品生产地提供服务.农产品物流中心5个备选地点的具体情况如表1所示.

经过分析，以尽可能多地覆盖农产品产地为原则，绘出了农产品物流中心备选地点及辐射面示意图(图1).

图1 农产品物流中心备选地点及辐射面示意

2 农产品物流中心选址影响因素分析

现代农产品物流中心在农产品物流中发挥着至关重要的作用.作为产销沟通桥梁，其合理的选址应达到整个物流系统能够加快物流过程、降低物流成本、提高物流作业效率等效果.考虑到农产品易腐、易变质的特性，本研究从交通条件、农产品产量、配套设施、地方政策和地形条件5个方面进行分析，以便科学合理地进行选址.

(1)交通条件.产品流通对交通运输有很高的要求，农产品物流中心也如此，其选址首先要考虑的因素是交通条件.农产品物流中心修建的地点必须方便产品运输，最好选址在交通枢纽附近.多种交通运输方式的采用有利于提高物流运输效率，对物流中心的发展有很重要的作用.

(2)农产品产量.为了服务于农产品物流中心周围地区的农产品生产和贸易，便于将产地农产品集中于物流中心，农产品物流中心应尽可能将业务辐射到更多的农产品生产基地.在物流中心的业务辐射范围内，必须考虑各农产品产地到物流中心的物流量，即产地的农产品产量.农产品物流中心选址应在靠近农产品产地的基础上考虑农产品产量.

(3)配套设施.农产品物流中心所在地区的配套设施或公共基础设施对物流中心的日常运转与发展影响很大.农产品物流中心选址在考虑其他因素的同时，需要考虑通信、能源、安全、土建、消防和环境等条件.物流中心占地面积较大，所用设施较多，可以尽量利用现有基础设施，以便减少建设费用.

(4)地方政策.农产品物流中心选址地区的物流产业优惠政策对农产品物流中心的经济效益有很重要的影响.地方政策和法规将直接影响农产品物流中心的运作.它包括政府对物流中心建设提供的用地、税收等方面的优惠措施和政策.

(5)地形条件.农产品物流中心应该选址在地势较高、地形较平坦的地方，而且要有足够的面积.完全平坦的地形最为理想，地势稍有坡度或者稍有起伏的地方也可，但不应该选址在山区或是陡坡地区.物流中心的占地外形以长方形较为合适，不宜选址在狭长或不规则外形的区域.

3 基于AHP的农产品二级物流节点选址

层次分析法(AHP)是美国运筹学家Saaty提出的一种多目标、多准则的分析方法，是一种定量与定性分析相结合的科学合理的决策方法.层次分析法适用于存在不确定性和主观信息的情况，最大的优点是提出了层次本身，能够认真地考虑和衡量指标的相对重要性.在AHP中，首先，复杂问题被分解成各个组成因素，并按照从属关系将这些因素分组，构成递阶的层次结构；其次，通过各因素之间两两相互对比的方式确定在层次结构中各个因素的相对重要性；然后，结合相关人员的评价判断，按照备选方案的相对重要性对其进行总排序.其整个过程体现了人们在解决问题时，先对问题进行分解，再判断，最后综合的思维特性.

3.1 AHP的相关参数及计算公式

i、j：影响选址的的因素Bi和Bj的i、j行列.

n：总的因素个数.

ai j：因素Bi与因素Bj相比较的重要性标度.

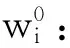
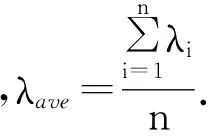
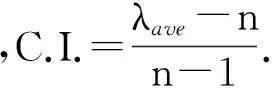
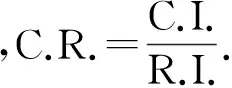
R.I.：平均随机一致性指标[7].

3.2 农产品物流中心选址评价指标体系

在进行选址时，需要充分考虑选址的影响因素以及选址的基本原则和要求，分析后，根据基本要素之间的关系建立系统的递阶层次结构即评价指标体系.在农产品物流中心选址方案(A)中，对农产品物流中心选址影响因素进行分析，得出影响物流中心选址的5个重要因素，即交通条件、农产品产量、配套设施、地方政策和地形条件，并分别设为B1、B2、B3、B4、B5，以此建立农产品物流中心的选址评价指标体系(图2).

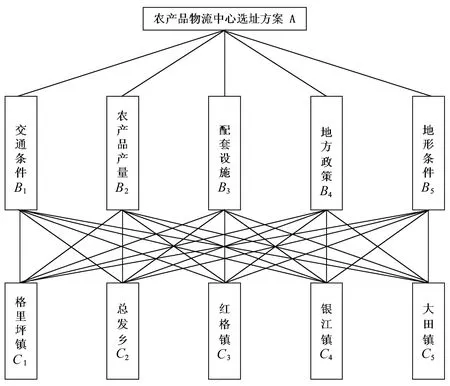
图2 农产品物流中心的选址评价指标体系

3.3 评价指标体系的要素判断矩阵及计算

3.3.1 AHP目标层判断矩阵及计算

采用德尔菲法进行评价打分，确定各因素的权重.根据德尔菲法对农产品物流中心选址影响因素进行评价打分，得出选址影响因素判断矩阵后，采用AHP进行重要度计算和一致性检验(表2).

3.3.1.1 要素重要度计算

归一化重要度为：

w1=(1×1×3×3×5)1/5=2.141,w2=2.141,w3=0.803,w4=0.803,w5=0.336.

相对归一化重要度为：

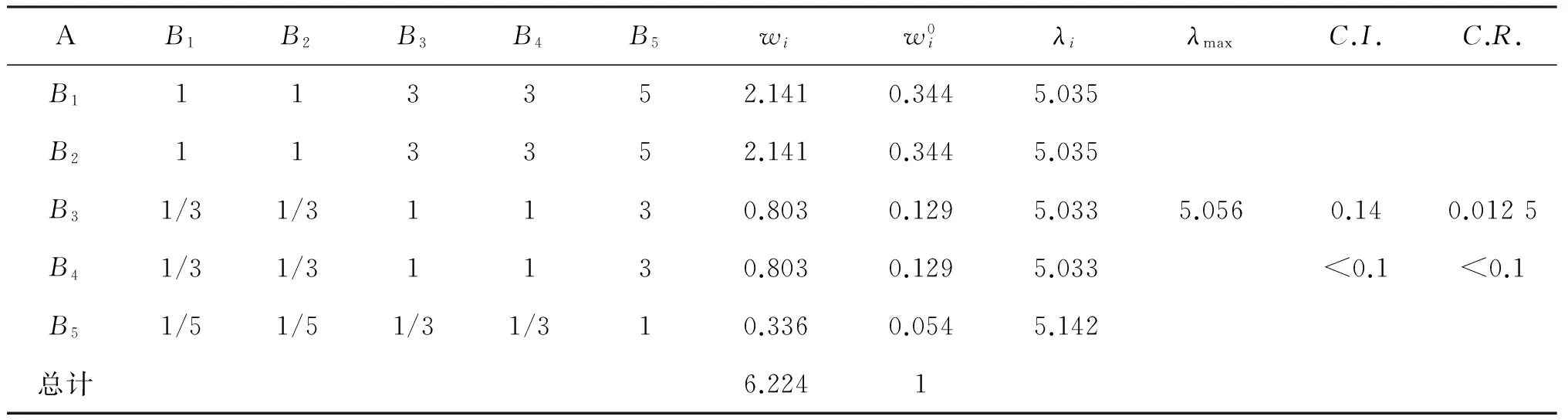
表2 AHP目标层判断矩阵重要度计算和一致性检验的结果

注：表中计算及检验结果数据无量纲.

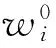
3.3.1.2 一致性指标C.I. 计算

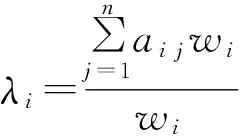
λ2=5.035,λ3=5.033,λ4=5.033,λ5=5.142.

计算结果如表2中λi所示.

3.3.1.3 一致性比例C.R. 计算

平均随机一致性指标R.I.是同阶随机判断矩阵一致性指标的平均值(表3)[7].引入它，可在一定程度上克服一致性判断指标随n增大而明显增大的弊端.

表3 平均随机一致性指标

注：表中数据无量纲.

当n=5时，R.I.=1.12，所以

对于3阶以上的判断矩阵，当C.R.<0.1时，即专家判断所得一致性和随机判断一致性之比小于10%时，可以认为该判断矩阵的一致性是可行的.反之，当C.R.>0.1时，需要对判断矩阵做适当修正，以确保一定程度的一致性.

由于计算出的C.I.和C.R.都小于0.1，因此选址影响的判断矩阵可行.计算得出，相对于目标方案A层的交通条件、农产品产量、配套设施、地方政策和地形条件的权重分别为：0.344、0.344、0.129、0.129、0.054.

3.3.2 AHP中间层判断矩阵及计算

根据以上计算方法，分别计算在交通条件B1、农产品产量B2、配套设施B3、地方政策B4、地形条件B5不同影响因素下各备选地点的权重(方法与目标层计算相似，此处省略计算步骤).

3.3.2.1 交通条件B1判断矩阵及计算

根据攀枝花各乡镇的交通状况，采用德尔菲法，结合专家意见，得出的交通条件在5个备选地点的相对重要度计算结果如表4所示.

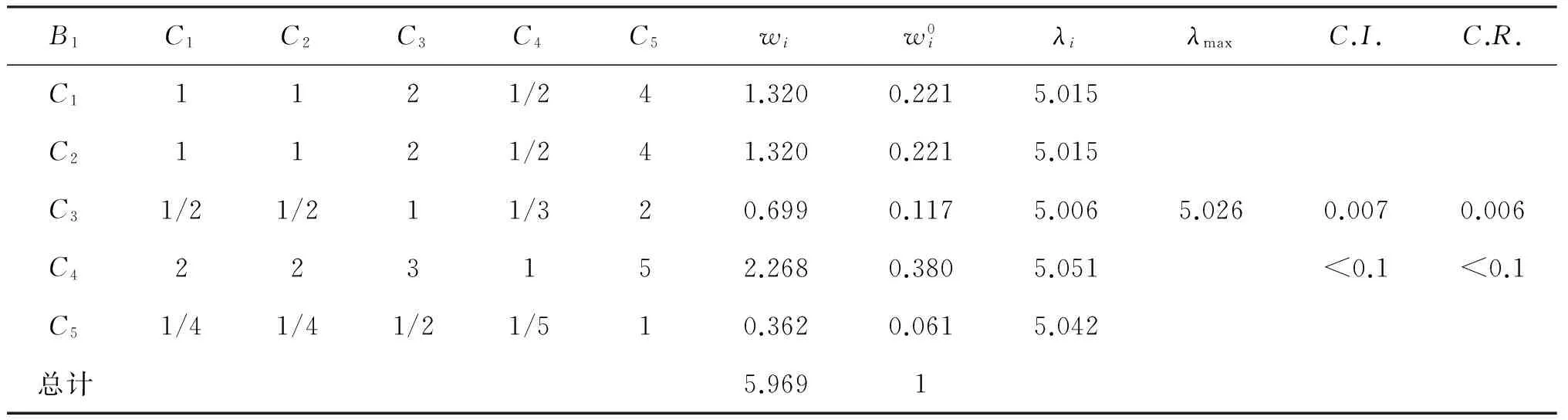
表4 交通条件判断矩阵重要度计算和一致性检验的结果

注：表中计算及检验结果数据无量纲.

通过一致性指标C.I.和一致性比例C.R.计算，得出的C.I.和C.R.都小于0.1.因此，在交通条件影响因素下，5个备选地点相对重要度的判断矩阵可行.

3.3.2.2 农产品产量B2判断矩阵及计算

根据攀枝花农产品产地分布情况以及主要产地的农产品产量，采用德尔菲法，结合专家意见，得出的农产品产量在5个备选地点的相对重要度计算结果如表5所示.

通过一致性指标C.I.和一致性比例C.R.计算，得出的C.I.和C.R.都小于0.1.因此，在农产品产量影响因素下， 5个备选地点相对重要度的判断矩阵可行.

表5 农产品产量判断矩阵重要度计算和一致性检验的结果

注：表中计算及检验结果数据无量纲.

3.3.2.3 配套设施B3判断矩阵及计算

根据攀枝花各区域公共基础设施情况，采用德尔菲法，结合专家意见，得出的配套设施在5个备选地点的相对重要度计算结果如表6所示.

通过一致性指标C.I.和一致性比例C.R.计算，得出的C.I.和C.R.都小于0.1.因此，在配套设施影响因素下，5个备选地点相对重要度的判断矩阵可行.

表6 配套设施判断矩阵重要度计算和一致性检验的结果

注：表中计算及检验结果数据无量纲.

3.3.2.4 地方政策B4判断矩阵及计算

根据攀枝花市政府对各区域农产品生产基地采取的各项政策以及各乡镇对农产品生产实施的优惠政策情况，采用德尔菲法，结合专家意见，得出的地方政策在5个备选地点的相对重要度计算结果如表7所示.

表7 地方政策判断矩阵重要度计算和一致性检验的结果

注：表中计算及性检验结果数据无量纲.

通过一致性指标C.I.和一致性比例C.R.计算，得出的C.I.和C.R.都小于0.1.因此，在地方政策影响因素下，5个备选地点相对重要度的判断矩阵可行.

3.3.2.5 地形条件B5判断矩阵及计算

根据攀枝花地形地貌，对各区域主要地形进行分析比较，采用德尔菲法，结合专家意见，得出的地形条件在5个备选地点的相对重要度计算结果如表8所示.

通过一致性指标C.I.和一致性比例C.R.计算，得出的C.I.和C.R.都小于0.1.因此，在地形条件影响因素下，5个备选地点相对重要度的判断矩阵可行.

表8 地形条件判断矩阵重要度计算和一致性检验的结果

注：表中计算及检验结果数据无量纲.

3.3.3 AHP方案总重要度矩阵及计算

计算得出各影响因素下各备选地点重要度后，可计算各备选地点总重要度(表9)，并进行排序.

表9 备选地点总重要度计算列表

注：表中数据无量纲.

计算各备选地点重要度：

C1=0.344×0.221+0.344×0.168+0.129×0.378+0.129×0.260+0.054×0.160=0.225

同理，计算出C2、C3、C4、C5的权重.显然，各备选地点C1、C2、C3、C4、C5所对应的权重为0.225、0.306、0.201、0.195、0.073，权重从大到小的顺序为C2、C1、C3、C4、C5.因此，物流中心选址应选在C1、C2、C33个地点，即对应的格里坪镇、总发乡和红格镇.

4 基于Floyd算法的农产品物流枢纽中心选址

4.1 Floyd算法的相关参数

i、j、r：农产品物流节点.

n：农产品物流节点总数.

ci j：节点i到节点j的距离.

4.2 农产品生产地交通关系图

在攀枝花物流系统中，选择一个农产品枢纽中心作为快速反应中心，既可以负责物流中心的各项运营，也可以对物流中心出现的问题进行快速应对，以保证攀枝花物流系统的正常运行.本文采用Floyd算法对农产品枢纽中心进行选址，以“使最大服务距离达到最小”为标准进行计算.

以农产品产量较大且较为主要的生产地来考虑枢纽中心的选址，包括农产品物流中心选址的几个主要备选地点总共8个可供选择的地点，分别为格里坪镇、务本乡、银江镇、太平乡、桐子林镇、红格镇、总发乡和大田镇.其中大田镇最为特殊，除总发乡以外并无其他备选地点可以直接到达大田镇，要到达大田镇必须经过总发乡.若在选址计算过程中将大田镇作为一个备选地点进行选址会影响计算结果，造成选址结果不正确.因此，选址计算不将大田镇作为备选地点.这样，备选地点为除去大田镇的7个地点，可分别设为V1、V2、V3、V4、V5、V6、V7，使用Floyd算法计算任意两点之间的最短距离.

图3所示为7个备选地点的交通关系图.

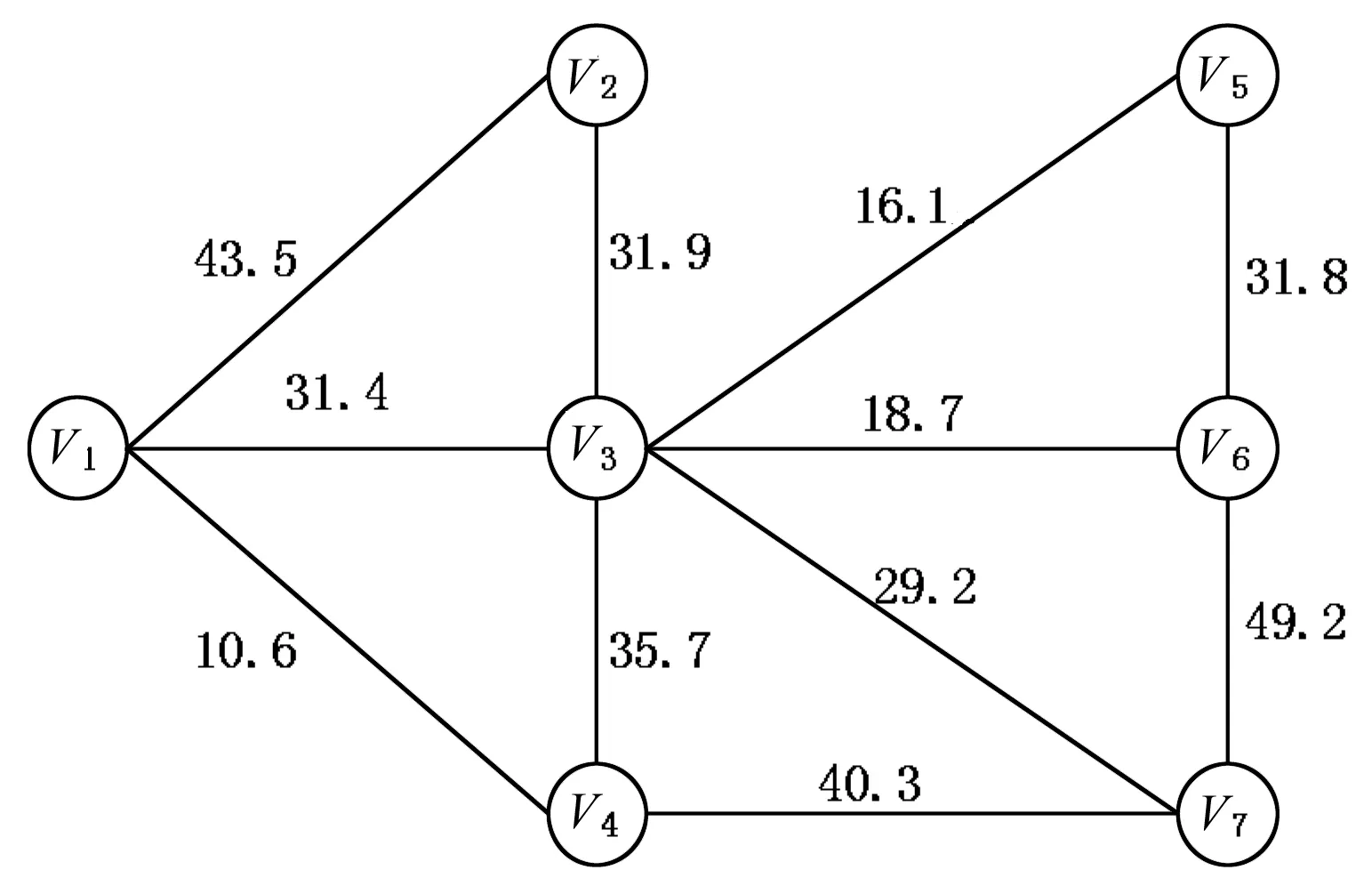
注：图中数据的单位为km.图3 备选地点的交通关系图

4.3 Floyd算法的最短距离表及最佳选择地

求得最短距离L3(表11).L3表与L4表相同.分析可知，L3表是最优表.

表10 最短距离L1表 km

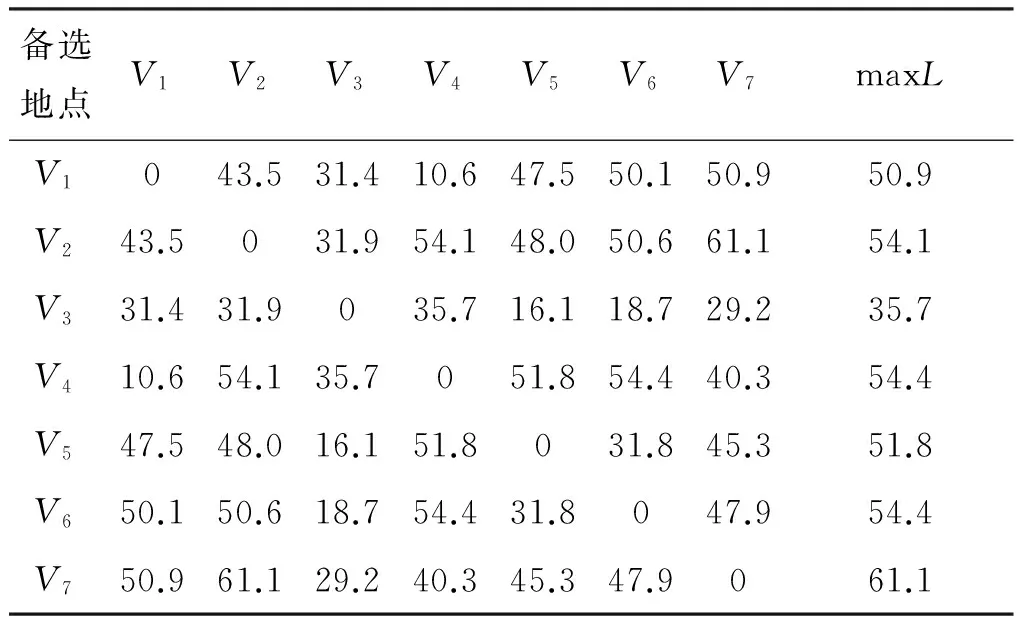
表11 最短距离L3表 km

根据L3表，由L=minmax{Li j}计算最短距离表中每行的最大距离的最小值，得出的L所在行对应的点就是最佳的选址地点.

最小值L=min{50.9,54.1,35.7,54.4,51.8,54.4,61.1}=35.7.在表11中，35.7位于第三行，则表示V3最佳.因此，选择V3对应的银江镇为攀枝花农产品枢纽中心选址地点.

进行攀枝花农产品物流中心选址研究后，得到格里坪镇、红格镇和总发乡3个物流中心以及银江镇1个农产品物流枢纽中心.图4所示为攀枝花农产品物流中心和枢纽中心以及几个农产品主要产地连线.

图4 农产品物流中心及枢纽中心与产地连线

5 结束语

本文分析了农产品物流现状，结合农产品特性，以攀枝花农产品为实例，构建农产品二级物流节点至物流中心的物流网络.用AHP对农产品二级物流节点进行了定量和定性的选址分析，设计了最适合农产品集散的物流中心建设地址和数量.用Floyd算法确定了攀枝花市的农产品物流枢纽中心的选址方案，构建了攀枝花市农产品物流网络，为当地农业经济发展起到了一定的促进作用.

[1] Holmberg K. Exact solution methods for uncapacitated location problem with convex transportation costs[J]. European Journal of Operational Research,1999,114(1): 127-140.

[2] 黄祖辉,刘东英.我国农产品物流体系建设与制度分析[J].农业经济问题,2005(4):49-53.

[3] 黄湘民,刘大成.剖析我国农产品物流发展现状及挑战[J].商场现代化,2006(16):117-120.

[4] 陈 超,李 冰.城镇化背景下我国农产品物流发展现状和问题及对策[J].农业现代化研究,2013,34(3):328-332.

[5] 索志林,王 栋.农产品物流中心选址模型及其应用研究[J].农业技术经济，2007(6):51-55.

[6] 许金立.基于供应链战略协同的农产品物流运行机制研究[D].北京:北京交通大学,2012.

Research on Site Selection of Agricultural Products Logistics Centers Based on AHP & Floyd Algorithm

ZHAO Yan-lin, LI Qin,WEN Zhong-bo, ZHOU Zhen-bing

(Panzhihua University, Panzhihua 617000, China)

This paper takes the site selection of agricultural products logistics centers as the research object and the agricultural products of Panzhihua as example to establish the logistic net from villages to the logisric centers combined with the features of the agricultural products based on the analysis of current conditions of agricultural products both home and abroad. And then, designing the most suitable location & number as well as the feasible plan for site selection of the logistic centers for the agricultural products of Panzhihua based on AHP and Floyd algorithm by fully analyzing the distribution conditions of the agricultural products of Panzhihua and fully considering the main factors and delivery route as well as the site selection of village nodes and zone centers to improve the problems which limit the economic development of Panzhihua, such as high logistic cost, high loss of the products and long delivery period etc.

agricultural products logistics;logistics center;site selection;AHP;Floyd algorithm

2016-11-14

赵晏林(1988-)，男，四川广安人，硕士，助教，研究方向为物流管理、工业工程和精益生产.

1006-3269(2017)01-0039-09

U116.2

A

10.3969/j.issn.1006-3269.2017.01.009