情境:接轨经验,促进认知
2017-04-14罗永军
◇罗永军
一、情境创设是为了促进数学理解
为什么在教学时要创设情境?大致有三个原因:(1)在情境中学习有一种浸入感,有利于激发学生积极的学习情感;(2)在情境中学习有一种代入感,有利于唤起学生原有认知经验,促使学生主动地、富有个性地学习;(3)在情境中学习有一种认同感,有利于建立数学与生活、数学内部之间的联系,促进数学理解,提升问题解决能力。
情境这么重要,每节课都要创设吗?不同的课型有不同的学习任务和目标,不是每节课都需要创设情境。我们应该尽可能创设内容丰富的情境,但我们也要明白创设情境是教学手段,而不是目的。从数学课标要求看,并没有要求情境必须联系生活,能与学生原有知识背景相联系,同时会使其产生新的认知冲突,从而获得良好的数学发展的情境,都是好情境。
二、生活情境与纯数学情境各有所长
两类情境哪一类更重要呢?数学课标强调的是情境的教学价值,我们对“生活情境”和“纯数学情境”的理解与应用也不妨聚焦于它们的教学价值。
1.生活情境。
在小学阶段,几乎所有的数学知识,都可以在生活实际中找到背景。
在小学低年级阶段,学生所感知的生活面比较窄,可以从他们身边熟悉的、有趣的事物中选取学习素材,创设情境。这样做容易激发学生学习数学的兴趣,使他们感受到数学就在自己的身边,易于他们理解相关的数学知识,体会到数学的作用。
例如,对于“乘法的认识”,现有各版本教材都引入了生活情境。浙教版教材用的是图1所示的“游乐场”情境。在图1所示的各个场景中,学生进行连加运算:坐在椅子上的人有3+2+4+3(个),玩转盘的人有4+4+4+4+4(个)……进而,在运算的比较中自然地引出了“乘法”。
同时我们要理解,对低龄儿童来说,小动物、植物、太阳、月亮等自然对象与人一样,是他们生活的一部分,是生活情境的重要素材。

图1 浙教版(修订前)一年级下册
从小学三年级开始,进入到皮亚杰划分的具体运算阶段、形式运算阶段,学生的活动空间有较大的扩展,他们感兴趣的问题已拓展到客观世界的许多方面,他们关注的对象逐渐转向自然界、社会生活中更为广泛的现象和问题,对具有挑战性的内容表现出更大兴趣。因此,教学时所创设的情境应尽量来源于自然界、社会生活中的现象和问题,如与现实生活有关的图片和视频,以使学生感受到数学的价值和趣味。
2.纯数学情境。
创设纯数学情境,不仅有利于学生理解所学知识的内涵,还能更好地揭示相关数学知识间的内在关联,有利于学生从整体上理解数学,构建数学认知结构。
例如,素数与合数的认识,在生活中当然也能找到相关案例,如“周期蝉的生命周期”。但像图2所示的情境“同学排队哪些能成长方形”就不那么直观且容易引起异议。事实上,每次引用这一情境时,学生都会认为7个同学排成的不是长方形,而是一条“线”。像这样难以和经验接轨、不利于生成数学对象的情境,与其这样牵强附会,不如直接聚焦于纯数学情境。因此,2010年浙教版修订时把这一情境更改为“用小正方形拼组成长方形”的操作情境(如图3)。通过操作、分类、比较,学生发现长方形的种类和数本身的分解属性有关,有的数(素数)只能分解为2个因数,有的数(合数)有更多的因数。

图2 浙教版(修订前)四年级下册
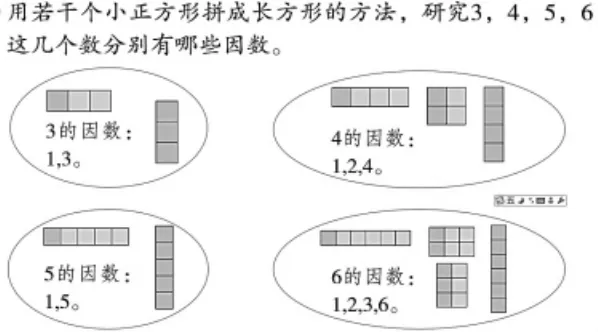
图3 浙教版(修订后)四年级下册
与“数的整除”单元类似,“分数的乘、除法”也常以纯数学情境引入。一般来说,数学内部发展出来的数学知识宜遵循知识的生长脉络,不要硬套生活情境。事实上,生活情境和纯数学情境都能落实课程目标,都有丰富的教学价值,同样重要。
三、数学情境构建的建议
1.纯数学情境。
构建纯数学情境的方式和途径有以下几种:
(1)知识迁移。在知识链中利用知识点之间的关系构建、创设问题情境,促进概念同化。比如,异分母分数加、减法的学习。
(2)几何直观。构建图形情境,利用图形的直观性呈现数学对象的内涵。比如,分数乘分数的教学。
(3)实验操作。构建实验情境,在实验过程中感悟数学对象、算理、算法,适合概念教学、问题解决等综合实践活动。比如,素数与合数的认识。
2.生活情境。
生活情境虽然对学生的数学学习有较大促进作用,但使用不当,效果会适得其反。比如,常见的学生“被春游”“被购物”情境,反让学生产生“数学很假”的认识。如何让数学情境更有效呢?
(1)动态素材,贯通课堂。尽可能设计或选择能衍生出一连串环环相扣、由浅入深的问题的动态情境贯穿整个课堂,使学生能从局部、整体、不同视角理解数学。以“乘法的认识”为例,常用的是“游乐场”情境(如图1),在情境中学生发现“同数连加”进而引出“乘法”,毫无疑问,这是好情境。我们再推荐一个更开放的“魔术表演”的情境(如图4),在这个表演剧场里,不仅有静态的同数连加:彩灯总数、灯笼总数等,更有神奇的魔术表演,魔术师从帽子里已经“变”出了2+2+2=6(枝)花,下一束花正要“飞”出来,孩子们看着魔术帽不由自主地想象着一连串的“2”,一共有多少呢?这就是“同数连加”。当然,也有学生想到可能会变出其他数量的花朵,毕竟魔术是很神奇的,常常令人意想不到,而这正好可以用来对比“同数连加”“不同数连加”之间的区别与联系。同样,另一位魔术师则变出了一缸缸金鱼,总共是4+4+4+4=16(条)或更多。像这样的情境,之所以能贯穿课堂,是因为其中的内容具有不充分性,必须进行“脑补”,学习素材由学生提供,进而加工、提炼,形成数学概念、法则。这是一种值得关注的情境构建方法,它的特点是学生能在情境中由消费者转变为创造者。

图4 青岛版二年级上册
(2)设置冲突,聚焦问题。在具体情境中设置挑战性问题,形成思维空间,激发学生的问题意识和解决问题的求知欲是一种重要的情境构建策略。比如,小数除法中,当除数是小数时,学生容易出现错误。因此,我们可以在教学中引入情境“谁打电话的时间长”(如图5)。它会引起学生怎样的冲突呢?
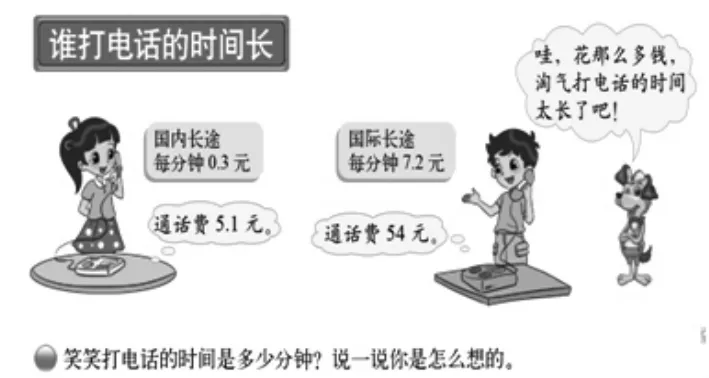
图5 北师大版五年级上册
我们曾对105位同学做过前测,90.5%的同学以为淘气打电话的时间长,因为通话费多,这是以往经验在起干扰作用。这种“错觉”与“冲突”为进一步的笔算、精算学习提供了情感铺垫和认知准备。此外,这一情境能和学生的经验自然接轨,所以它还能提供算法的校验功能:计算的结果是否正确。在前测中,我们发现计算结果是5.1÷0.3=0.17的学生最多(71.4%)。在教学时,有学生再次得到这个结果时,引起了其他人的质疑:0.17分钟?1分钟都不到?生活经验提醒学生,就算通话时间不到1分钟也按1分钟收费,5.1元比0.3元多多了,所以会大大超过1分钟。像这样的情境,不仅提供了内容背景,更提供了认知冲突,使得学习自然、深入。
(3)合理高仿,通情达理。改造现实情境,使其中的背景信息符合现实生活场景、儿童认知场景,且能聚焦其中的数学信息。情境固然需要真实,但不需要过多的细节,这个“度”的把握以有利于提炼出数学概念、方法和模型为宜。以乘法的认识为例,“游乐场”是常用的生活情境,不少教材都在使用。“游乐场”其实是对现实的一种高仿、一种处理过的真实。现实中游乐场中的信息大多是随机的,如游人总数、游客手中的气球数等,像“转盘”这些不热门的项目更是常有空位,同数连加的现象并不多。但作为教学任务的“游乐场”,情境中的“小火车”“转盘”“摩天轮”“气球”“杂技”“小黄花”“长椅上休息的人”等项目、对象,都是为了让学生去生成“同数连加、不同数连加”,从而构建出来的理想的模型。
事实上,我们在讨论要不要情境、要构建什么类型的情境、如何以情境为中心展开教学等问题时,都要清醒地认识到这些现象层面的问题,最重要的是要反思以下更为基础的本质问题:为什么要用情境?所用的情境能不能帮助学生接轨经验从而促进认知?等等。
