巧设情境，妙明算理，重育思想——“异分母分数加、减法”教学设计及评析

◇设计、执教/沈　强　评析/蓝海鹏

【教学过程】

一、数形结合，理解减法算理

1.比鞋跟的高度。

情境：在你家的鞋柜里，你爸爸的鞋多还是你妈妈的鞋多？在我家的鞋柜里，是我爱人的鞋多，我们来看看（出示图1）,如果我爱人穿上内增高鞋，比穿帆布鞋高多少分米？你能算一算吗？

学生列式解答。

选取学生的两种解答：

师：你能看懂这两种方法吗？

生：第一种是把分数化成小数，再相减。

生：第二种是把分数通分，把分母化成10，变成同分母分数，再相减。

师：异分母分数为什么不能直接相减？为什么通分后可以相减呢？

学生思考片刻，教师出示线段图（如图2）。

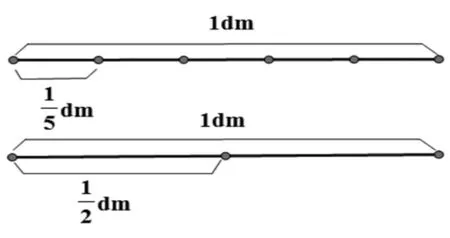
图2

生：看不出来。

师：怎么做才能让大家一看就知道相差多少？

生：可以再分一分。

生：可以把两条线段都平均分成10份。

师：请你在练习纸上分一分。

学生动手分，然后同桌之间交流。

师：（出示学生的作品，如图3）现在你们能一眼看出来吗？

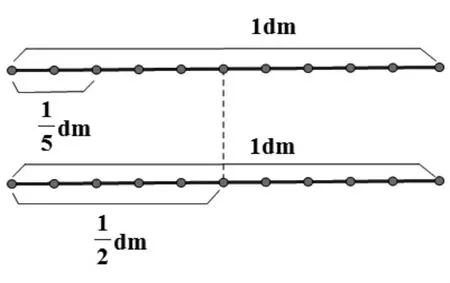
图3

师：现在为什么就行了？

生：因为都平均分成了10份，一个有2份，另一个有5份，相差3份。

评析：通过创设熟悉的生活情境提出问题，激励学生调用经验尝试解决新问题。学生通过课前预习，初步了解了通分的方法，但不清楚“为什么”。利用线段图，让学生直观地发现：分母不同的分数相减不能一眼看出结果，启发学生把异分母分数转化为同分母分数后再计算。通过对比、分析多种算法，理解各种算法蕴含的算理，为进一步开展通分教学打下基础，使学生初步感受通分在异分母分数加、减运算中的必要性。

2.比上班的时间。

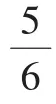
生：谁先到办公室？

生：谁走得快？

师：你们帮我算一算：谁走得快？快几时？

学生列式计算。

选取学生的两种算式：

师：还有其他方法吗？

生：化成小数再计算。

师：可以吗？

学生在小组内交流自己的想法。

生：相同点是：都进行了通分，化成了同分母分数。

生：不同点是：一种是把分母通分成最小公倍数12，另一种是把分母通分成公倍数24。

师：用这两种方法都能算出结果，第一种更简便，因为公分母12是两个分母的最小公倍数。

评析：借助恰当的生活情境，提出异分母分数减法运算的问题，鼓励学生从情境中提出问题。从多种算法中，学生感受到化为小数已经不能精确地解决此问题，必须通过通分来计算，进一步感受到学习通分的必要性。通过情境教学，学生进一步学会了通分的基本方法。

二、利用七巧板，理解加法算理

师：刚才我们学习了异分母分数减法，接下来我们看看异分母分数加法，看看算理是否一样。

出示七巧板，提出问题。

师：这里有一幅七巧板拼图（出示图4），把整个图形看作“1”。

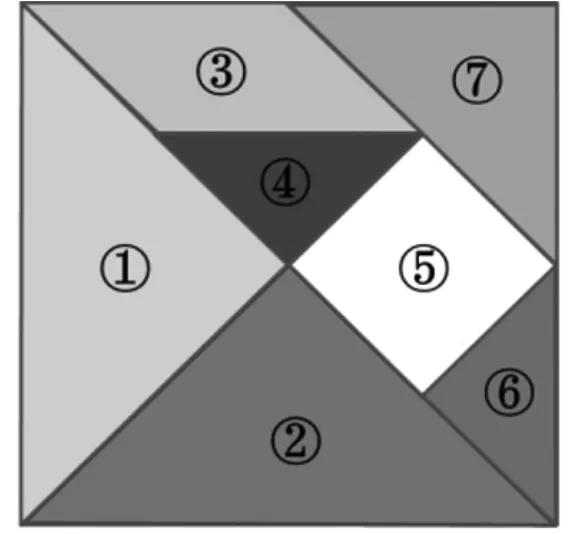
图4

问题1：各部分分别占了几分之几？

学生动手在“七巧板练习纸”上画线、分析，并回答。

问题2：②+⑦=？请列式计算，并跟同伴说说你是怎么想的。

学生独立思考、操作后回答。

师：你能从图中看出它们合起来是多少吗？

生：看不出来。

师：你是怎么操作的？

生：把整个图形平均分成8份（如图5）。

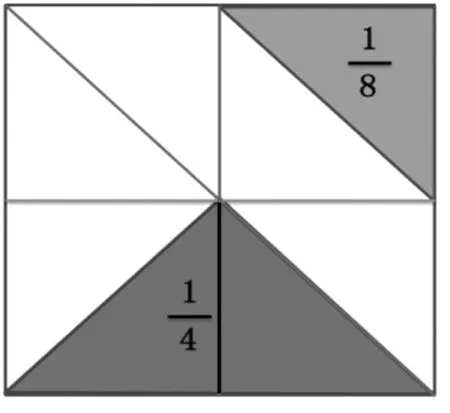
图5

师：现在你能看出它们合起来是多少吗？

师：刚才我们把整个图形平均分成了8份，正好可以解释通分的过程。

学生讨论，用图形展示通分的过程，教师演示。

小结：异分母分数加法计算的方法，跟减法一样，都是先通过通分化成同分母分数，再计算。

问题4：你能说说异分母分数加、减法的计算方法吗？计算的关键是什么？需要注意哪些问题？

评析：借助七巧板情境，提出异分母分数加法问题。以梯度问题为引导，通过学生操作、几何画板动画演示等手段，利用图形表征、解释通分的过程，帮助学生理解算理。学生在经历以上三个情境问题解决的基础上，总结出异分母分数加、减运算的方法。

三、沟通小学阶段加、减法的算理

问题1：回顾一下，在列竖式时，我总是提醒你们小数点对齐或末位对齐，这是为什么?

问题2：在小学阶段，我们学习过整数的加、减法和小数的加、减法，它们的算理跟今天学习的分数加、减法一样吗？

师生共同交流，得出结论：数位对齐了，计数单位也就对齐了。小学阶段所学的整数、小数、分数加、减法，都是相同计数单位个数相加、减。

师板书：相同计数单位个数的加、减。

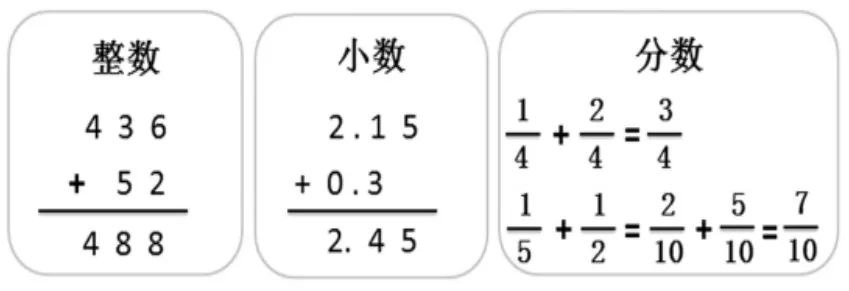
图6

评析：通过分析整数、小数、分数加、减法的算理，沟通它们的内在联系，点明本质：相同计数单位个数的加、减。

四、利用游戏，提高计算能力

1.卡片游戏。

2.全班交流，小组派代表进行比拼。

评析：单纯的计算训练是枯燥的，创设游戏情境，能激发学生参与练习的积极性，在寓教于乐中巩固所学方法。

【总评】

一、巧设情景，活用教材

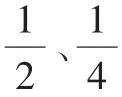
二、妙明算理，重育思想

1.重视转化思想的培养。

（1）“在旧知中发现新知”“迁移旧方法解决新问题”：从熟悉的情境中发现新问题，并用生活经验和旧知（转化为小数的方法）解决异分母分数加、减法情境问题，实现了把已知方法迁移运用到新问题情境中。

（2）“化未知为已知”：整个教学过程，非常重视把未知的异分母分数加、减转化为已知的同分母分数加、减来计算的理解、运用过程。

2.重视利用数形结合思想，理解算理。

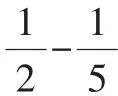
3.注重知识联系，突出思想本质。

借助竖式，对比整数、小数、分数加、减法的计算方法，说明计算时相同计数单位要对齐，也是在沟通不同计算模块的算理，点明三种计算模块共同的本质。

三、对比算法，优化思维