多做题，会做题，巧做题

彭慧

[摘 要] 自主高效的数学学习离不开兴趣与热情的激励. 高中数学抽象、枯燥，想要让学生从心底焕发出主动学习的动力，为了能让学生在完成必要习题的同时不失学习热情，教师就需要从习题本身入手，通过增加习题趣味的方式来提升教学实效.

[关键词] 数学；趣味；习题

学习数学总是少不了做题，在高中阶段的知识学习当中，更是出现了数量较多、难度较大的习题. 对于学生来讲，想要高质量地接受这些习题并不是一件容易的事情. 一方面，数量增加的习题，为学生添加了不小的课业负担；另一方面，难度增加的习题，对学生的思维能力来讲提出了很大的挑战. 这些都难免会引发学生对于高中数学学习的畏惧与抵触心理，而这也必然成为阻碍高效学习推进的内在因素. 为了能让学生在完成必要习题的同时不失学习热情，教师们就需要从习题本身入手，通过增加习题趣味的方式来提升教学实效.

[?] 运用创新性习题，增加关注趣味

数学学习进入到高中阶段之后，灵活性顯著增强. 也正是这种灵活性的存在，为题目趣味的挖掘提供了多种可能. 对题目呈现的方式进行细致分析便会发现，虽然都是对知识内容进行训练，题目形式却不一定都要以一成不变的形态来进行. 将题目形式加以创新，将待考查的内容与全新的途径融合起来，将会为学生带来不一样的练习感受.

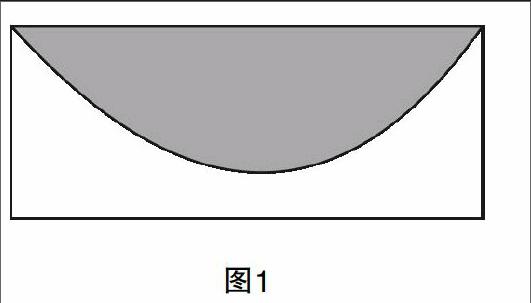
例如，在对概率统计的内容进行教学时，笔者多次引入了创新性习题. 这部分知识内容虽然不是各类考试当中的得分重点，却是在每次测试当中都会出现的. 若掌握得好，将会成为历次测试中的平稳得分点；而若是掌握不好，即使其他部分答得再好，也无法弥补这部分问题的失分. 对于这部分内容的教学，需要在不耗费过多时间、精力的基础上达到优质效果. 为此，笔者选择从习题设计形式上加以趣味创新，让兴趣推动高效学习的进行. 如图1所示，在一个水平放置的矩形平面上随机撒出300个小球，且该矩形的宽是2，长是5. 经统计，在图中阴影部分里散落了138个小球. 由此，能否估算出阴影部分的面积？表面看来，阴影部分是一个不规则图形，运用公式计算面积显然是不可能的. 当学生想到了概率统计的方法之后，立刻恍然大悟. 这种创新性的问题设置，刷新了学生对于这部分知识考查的惯常理解，新颖性和趣味性都提升了不少.

从问题形式上加以创新，能够让学生从接触习题一开始就有一个耳目一新的感觉. 这种新鲜感往往就是推动学生启动思考的原动力. 将知识内容隐藏得深一些，为习题多添加一些单纯题目之外的叙述与形态，便可以为习题增加诸多趣味，引导学生快乐地展开思考.

[?] 运用层次性习题，增加思考趣味

将一个难度较大的问题直截了当地摆出来，总是会对学生的思维能力提出严峻考验，这也很容易让学生失去对思考的激情. 这时，如果能够将习题进行一种层次化设计，将一个难度较大的问题拆分为两个或是更多数量的小问题予以提出，在降低思考难度的同时，也会为习题本身增加不少趣味.

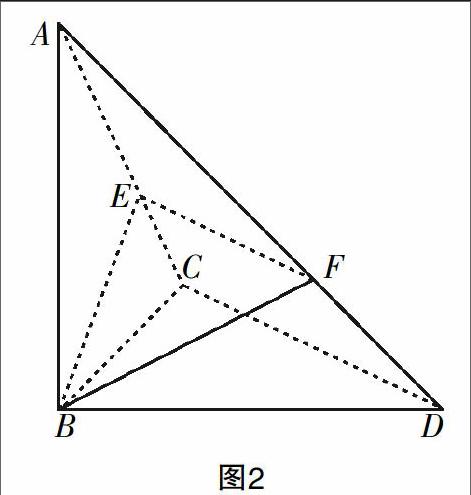
例如，在对立体几何内容进行教学时，笔者曾经在课堂上设计了这样一道习题：如图2所示，在四面体的底面△BCD中，∠BCD是一个直角，BC边与CD边的长均为1，且AB与底面BCD垂直，∠ADB的度数是60°. 在AC边与AD边上分别有动点E，F，其中，AE与AC的长度之比同AF与AD的长度之比相等，均为λ（0<λ<1）. （1）求证：无论λ的取值如何，都有平面ABC与平面BEF垂直. （2）若要使得平面ACD与平面BEF垂直，应当将λ的值确定为多少？

如果直接将第二个问题提出，对于学生思维的挑战是很大的，也很容易让知识能力一般的学生畏惧、远离. 而多设置了第一问进行铺垫之后，习题的分析难度有所降低，也在无形之中提示了解题方向. 在这种层次性解题的搭建之下，学生更加乐于投入到逐个问题的思考当中. 一次次小问题的成功解答，也会持续不断地为学生提供心理上的自信，鼓励他们的思考逐渐走向深入.

每个问题的推理思考都是存在一个循序渐进的思维过程的，将这个思维过程当中的重要节点摘要出来，设计成为一个问题，就会形成一个层次性深化的问题串. 这种层次性习题的设置，从教学技术角度来讲并不困难，却可以为整个习题思考过程增加很多思考趣味.

[?] 运用实践性习题，增加应用趣味

让学生感到高中数学知识枯燥的原因主要是其理论性过强. 的确，对于这个年龄阶段的学生来讲，大面积、持续性的纯理论覆盖，很容易让他们觉得毫无学习兴趣可言. 这时，如果能在理论之中适当加入一些实际应用的元素，便能够大大改善这种现状. 应用的过程本身就是一种趣味，它不仅可以为单一的学习过程转换气氛，还可以为学生带来学以致用的成就感.

例如，在对球体的内容进行教学时，笔者先向学生介绍了基本概念与公式等内容. 待大家对这部分知识较好地掌握之后，笔者在课堂上引入了这样一道习题：如图3所示，在水平地面上有一个透明材料制成的正方体容器，且正上方没有盖子，容器的边长是8厘米. 有一个球形物体，其大小正好可以卡在正方体容器口上. 现向该容器中加水，直至水面正好与球面相接触，此时容器内的水深度达到了6厘米. 若容器侧壁与底面的厚度可以忽略不计，则这个球体的体积是多少？这个问题虽然很明确地对球体的体积计算知识进行了考查，但却是以一个实践的形态加以呈现的. 这个方式很好地让学生体会到了应用的趣味，在实际操作的感知下提升了知识适用的效果.

应用问题在高中数学的各类测试当中并不鲜见，将之运用到课堂教学过程之中去也很方便. 在实践性习题的带动下，学生的数学思维很自然地从课本上迁移到了生活中，不仅看到了数学知识的全新面貌，更在应用的同时完成了更为深化灵活的知识理解，显著提升了习题训练的实际效果.

[?] 运用灵活性习题，增加延伸趣味

每一个模块的数学知识都不是停滞不动的，而总是存在着拓展与延伸的空间. 这既是高中数学学习的挑战所在，也是趣味之处. 将基础性的习题不断进行灵活变化，引导学生的知识思维走向开阔，也是增加习题趣味的另一个有效途径. 这样的习题常常可以将数学的生命力展现出来，让学生逐渐喜欢上思考的感觉.

例如，在对三角函数的内容进行教学时，为了能够将学生的思维打开，笔者特意设计了这样一道习题：一调研小组希望掌握某海域海浪高度的变化规律，进而制定出一份关于该海域是否适合开展冲浪运动的报告. 他们构建了一个函数y=f（t），其中，y（单位：m）表示该海域的海浪高度，t（单位：时）（0≤t≤24）则表示时间. 通过对海浪高度进行全天候测量，记录数据如表1所示. 观察分析后发现，函数y=f（t）的曲线可以近似地视为函数y=Acosωt+b（ω>0）. （1）结合表格当中的数据，写出函数y=Acosωt+b的表达式及其振幅A和最小正周期T. （2）为了保证安全，只有海浪高度超过1 m时，才能进行冲浪运动. 那么，在每天8：00至20：00的时间区间内，适合进行冲浪运动的时间有多少？这个问题在三角函数基本知识的基础上进行了一个灵活拓展，成功摆脱了死板的公式套用，借助探究问题调动了知识运用. 在这样的过程中，学生的参与热情得到了显著提升.

从上述范例当中不难看出，运用灵活性习题开展教学对于高中数学教学来讲具有双重价值：一是实现了教学目标的要求，将学生的知识水平提升了一个档次；二是为问题的思考过程增加了很多灵活乐趣，成功吸引了学生的自发关注. 在教学过程当中多加入一些这样的习题，对于学习兴趣提示与知识理解延伸都是很有益处的.

自主高效的数学学习离不开兴趣与热情的激励. 特别是对于高中阶段的学习来讲，面对愈发抽象枯燥的知识内容，想要让学生从心底焕发主动学习的动力，就要从知识本身的优化入手. 高中数学内容虽然从抽象性与难度性上都有了不小提升，但是，其中的学习趣味仍然很多. 只要教师们能够将这些趣味发掘出来，就必然可以激发学生对之进行关注和探索的热情. 从本文当中的论述也不难发现，数学习题的趣味散发点是很多的，抓住这些切入点，便可以很顺利地在保质、保量的习题训练当中实现教学实效的提升.