向量表示：一种重要的数学问题解决思想

杨越

[摘 要] 向量具有丰富的物理背景，也是几何与代数的研究对象，是沟通几何与代数的桥梁的重要数学模型. 在高中数学中，向量是一个较为特殊的核心概念. 本文结合高中数学应用向量思想方法解决数学问题的三种主要表示形式，具体分析了利用向量表示优化解题的一般策略. 它将突出向量的工具性作用与解题的简洁性特点，能够有效地培养数学的创造性思维品质.

[关键词] 向量；向量表示；高中数学

数学思想，是数学内容的精髓，是知识转化为能力的桥梁. 向量具有丰富的物理背景，它同时也是几何与代数的研究对象，是沟通几何与代数的桥梁的重要数学模型思想. 在高中数学中，向量是一个较为特殊的核心概念. 一方面，向量具有方向、位置、长度、夹角等“形”的特征；另一方面，向量亦具有大小、正负、能像数一样运算等“数”的属性. 为了突出向量这一形数兼备的“二重性”，目前教材中先后提供了三种不同的表示方法：几何表示、数乘表示与坐标表示. 这些向量表示思想方法不仅深刻地揭示了向量知识的本质属性，其蕴含的数学思想也为我们理解数学问题与优化解题策略提供了更加广阔的思维发展空间.

[?] 向量的表示形式

在数学上，一个数学对象可以用某一特定的形式来表示，也可以用与其特定形式等价的另一种形式来表示. 对数学对象的思维、操作和运算是借助于它的表示形式来实现的. 适合的表示形式不仅能够直观地反映数学对象的特征，也有助于研究、建构数学对象之间的结构和关系. 对于向量，为了表示其有向线段的特性，通常用符号或a来表示. 此外，对于某一特定的非零向量而言，还有如下三种表示形式.

几何表示：向量可以表示为向量与的和，或向量与的差，即=+或=-. 向量的几何表示遵循平行四边形法则或三角形法则，其实质是，对某一特定向量，可以通过两个不同向量的组合来实现. 向量的几何表示反映了向量在方向、位置等“形”的方面的关系和属性，突显向量作为“有向线段”与“线段”的根本差异.

数乘表示：向量可以表示为与其平行的单位向量e与一个常数的乘积，即若向量的长度为k，则向量=ke. 在此基础上，我们可以进一步得出，平面上的任一非零向量都可以表示为两个单位向量的线性组合，即存在两个单位向量e1，e2，使得=k1e1+k2e2. 向量的数乘表示形式直观地反映了向量在大小和方向两个方面的特征.

坐标表示：以向量的始点A为坐标原点建立平面直角坐标系，若设向量在x轴、y轴上的投影坐标分别a，b，则向量=（a，b）. 向量的坐标表示实现了“形”与“数”的完美统一，即一个有向线段和一对有序实数对之间存在一一对应关系，实现了从“形的推理”到“数的运算”的转换.

三种表示形式试图从“形”和“数”两方面揭示向量的本质属性. 几何表示强调向量的“形”，可以刻画直线、平面、空间等几何对象的位置关系和度量性质. 坐标表示强调向量的“量”，可以参与代数运算. 数乘表示则二者兼具. 另外，三种表示形式之间并非完全独立，而是可以相互转化. 例如，在坐标表示中引入单位向量，即设x轴、y轴上的单位向量为i， j，则=（a，b）=ai+bj. 同样，在几何表示中引入单位向量，则可以实现几何表示与数乘表示的转换. 需要指出的是，上述二维平面的向量表示很容易推广到三维空间的向量表示.

[?] 利用向量表示优化解题策略

向量是数形结合的化身. 向量表示实现了从“形”到“数”或者从“数”到“形”的转化，为解决数学问题提供了强有力的工具. 适当选择向量的不同表示形式，将代数问题几何化，或者将几何问题代数化，有助于揭示数学问题背后所隐藏的数量关系、几何特征，理解数学问题的实质，优化解题策略. 下面举例说明利用向量表示解决问题的一般策略.

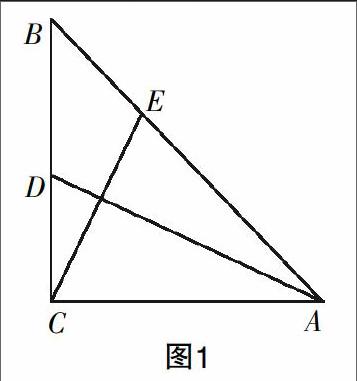
证明：根据向量的数量积，若两个非零向量的数量积为0，则这两个向量相互垂直. 要证AD⊥CE，即证明·=0成立即可. 为此，设CA=CB=m，注意到=+，=-，

于是·=（+）（-）=·-·+·-·

=m·m·-m·m·1+m·m·+m·m·0

=m2-m2+m2+0=0.

即·=0. 根据向量乘法性质可知，AD⊥CE.

上述证明的关键是，用向量表示问题所涉及的几何元素，将几何问题（AD⊥CE）转化为向量问题（·=0）. 通过向量运算，特别是向量的数量积运算，研究几何元素之间的关系，如垂直、平行、长度、角度等. 最后利用向量数量积的性质对运算结果做出几何解释.

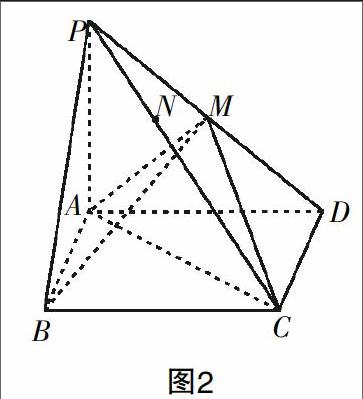
例2：如图2，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2. 以AC的中点O为球心、AC为直径的球面交PD于点M.

（1）求证：平面ABM⊥平面PCD；

（2）求直线CD与平面ACM所成的角的大小.

解：以A为坐标原点，AB，AD，AP所在的直线分别为x轴、y轴、z轴建立空间直角坐标系. 于是，A（0，0，0），B（2，0，0），D（0，4，0），P（0，0，4）.

（1）平面ABM⊥平面PCD的问题可以转化为证明PD与AB，AM或BM垂直的问题.

由于=（0，4，-4），=（2，0，0），=（0，2，2），

于是·=0，·=0，即PD⊥AB且PD⊥AM，

所以PD⊥平面ABM.

因为PD?平面PCD，

所以平面ABM⊥平面PCD.

（2）求直线CD与平面ACM的夹角可以转化为求直线CD与平面ACM的一条垂线所成的角.

设平面的法向量为n=（x，y，z），注意到=+=（2，0，0）+（0，4，0）=（2，4，0）.

根据n⊥且n⊥，得n·=（x，y，z）（2，4，0）=2x+4y=0 ①.

且n·=（x，y，z）（0，2，2）=2y+2z=0 ②.

联立①②求解，且取y=1，得法向量n=（-2，1，-1）.

设所求的夹角为α，于是可得cosα====.

所以直线CD与平面ACM的夹角是arccos.

利用向量表示，将几何对象向量化、数量化，最终运用代数运算处理面面、线线、线面等位置关系和度量性质的基本思路. 与几何方法相比，向量法是一种较为程序化的方法，其关键在于建立适当的坐标系并用向量表示其中的有关对象，进而将几何的推理转化为代数的运算.

例3：证明不等式+≥（m+n）2当0

证明：由a，b的数量积a·b=

可知，≥m+n>0.

所以+≥（m+n）2，當且仅当a∥b，即=时等号成立.

[?] 研究小结

代数符号的抽象表达有时构成了理解和解决问题的障碍. 对于诸如不等式、函数最值、解析几何、三角函数等一类解证问题，如果我们能够构造向量表示其中的数量关系，再借助于向量的几何直观或者运算性质，就容易发现或找到解决问题的思路和突破口，达到优化解题过程、降低解题难度的目的.

向量集“数”“形”于一身，是高中数学最基本的概念之一. 作为“数”，向量具有代数的一些运算性质；作为“形”，向量具有几何的直观推理属性. 因此，向量是数形结合思想的一般体现，是实现几何问题与代数问题相互转化的中介. 作为一种思想方法，向量法解决问题的关键在于用适当的向量表示其中的数学对象，从而将几何问题或代数问题转化为向量问题，进而利用向量的代数运算或直观推理获得问题的解答. 用向量表示解决数学问题的一般步骤可以归纳如下（见图3）：

[数学问题][向量问题][解 答][向量

表示] [代数运算] [直观

推理]

图3

概括起来，应用向量数学思想来解决问题，其目的是突出向量的工具性作用，发挥向量思想方法解题的简洁性和优越性的特点，在解题过程中发现数学原型，建立起更新的数学模型，推动数学学科发展，更主要的是可以有效地培养学生的数学创造性思维能力，提升数学学习的品质.