基于约化相对轨道拟平根数的长期稳定高精度卫星编队导航技术*

杨盛庆，杜耀珂，贾艳胜，王文妍

(1.上海航天控制技术研究所，上海201109;2.上海市空间智能控制技术重点实验室，上海201109)

基于约化相对轨道拟平根数的长期稳定高精度卫星编队导航技术*

杨盛庆1，2，杜耀珂1，2，贾艳胜1，2，王文妍1，2

(1.上海航天控制技术研究所，上海201109;2.上海市空间智能控制技术重点实验室，上海201109)

针对基于星间相对测量的相对导航算法中由测量方程将相对轨道拟平根数转化为相对位置过程导致的模型非线性，提出一种基于约化相对轨道拟平根数的卫星编队导航方法.该方法通过编队卫星之间一段时间的切向漂移估计半长轴偏差，合理处理半长轴偏差对双星相对动力学的影响，克服了模型线性化造成的误差，能够实现长期稳定的高精度卫星编队导航.

卫星编队;长期稳定;相对导航;约化相对轨道拟平根数;半长轴偏差

0 引言

随着卫星应用技术的发展，部分空间应用任务难以依靠单一的卫星来实现［1］.卫星编队的协同工作，是卫星技术发展的必然趋势.目前，卫星的编队任务大致可以分为合作目标的编队保持、空间交会对接和空间服务几大类.卫星相对运动、导航与控制的研究是实现编队任务的基础.卫星编队相对运动的研究，初期主要基于C-W方程，分析了卫星编队的自然周期相对运动解的存在性［2-4］，继而采用EKF/UKF算法实现了基于相对位置、速度的编队导航［5］.

针对近地观测卫星普遍选用近圆轨道的特点，国内外学者提出了基于相对轨道拟平根数的编队相对运动模型［6-8］.此类相对运动模型利用相对轨道拟平根数，克服了短周期项对导航模型的影响.由该模型衍生的编队构型参数是设计编队保持控制策略的有效依据.针对相对轨道拟平根数设计卫星编队导航算法，具有重要的研究意义.基于相对轨道拟平根数的编队相对运动模型是在等半长轴、等轨道倾角假设下得到的近似模型，描述的是卫星编队的自然周期相对运动［9-10］.近地卫星受大气阻力的影响较明显，设计长期稳定的编队导航算法时，必须考虑半长轴偏差造成的影响.

本文介绍了基于相对轨道拟平根数的编队导航算法，通过分析导航模型的非线性因素，定位导航算法中线性化误差的来源.通过引入半长轴偏差对模型的影响，提出了基于星间相对测量与相对轨道拟平根数的卫星编队导航方法，能够提供长期稳定和高精度的编队导航结果.

1 基于相对轨道拟平根数的编队相对运动

1.1 相对轨道拟平根数

定义相对轨道拟平根数［9-10］

式中，ak，ek，ik，ωk，Ωk，uk(k=1，2)均取轨道平根数，下标1表示目标星，下标2表示跟随星.同时定义标量δe，δi满足

基于相对轨道拟平根数的编队构型参数满足

式中，l可以理解为对升交点赤经偏差引起的切向偏差的估计值.不能简单地由纬度幅角偏差造成的a1Δu表述该切向偏差，因此引入补偿项a1coti1ΔiY，该公式对等半长轴的假设依赖性较强.

1.2 卫星编队的相对运动及其构型参数

［9］给出了卫星编队的相对运动方程.本文在其基础上考虑半长轴偏差Δa和切向偏差l的影响.图1为球面三角间的关系，由于ΔΩ为小量，ΔN1N2N3中边长N2N3=a1ΔΩsini1.根据等角关系有ΔN12N2N3～ΔN12S1S2，满足三角形相似定理N2N3/(a1sinφ)=S1S2/［a1sin(u1-φ)］.因此，相对位置可以表述为

式中，xH，yH，zH为编队坐标系下三轴变量.本文在参考文献［9］的基础上，分别在xH上加入半长轴偏差Δa，在yH上加入切向偏差l.

不妨记p=a1δe，s=a1δi，式(5)可改写为

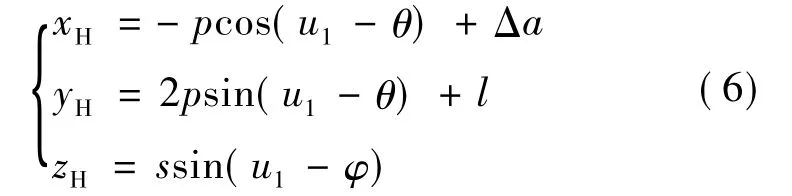
对式(6)求导得

图1 卫星编队的球面几何关系Fig.1 Spherical relationship of satellites formation

依据式(6)～(7)，编队构型参数p，s，θ，φ，l满足

2 基于星间测量的编队导航

2.1 观测量与编队导航方法

目前，星间相对测量的精度已满足编队导航的任务要求［11］.本文设计了基于星间相对测量的编队导航方法，即将星间测量的相对位置Z=［xHyHzH］T作为编队导航的观测量.

编队导航的关键是要描述好测量方程和状态方程.滤波器的状态变量为相对轨道拟平根数，而观测量为编队坐标系下的相对位置.测量方程表示两者之间的转换关系，根据球面几何的原理，测量方程和测量矩阵可以表述为［9-10］

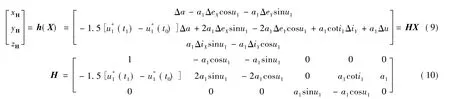
2.2 编队导航模型的线性化误差

编队导航滤波算法中，将每一步的状态预测值与测量值进行比较，以两者之间产生的偏差作为修正量的依据.由于测量值为相对位置，导航滤波的状态变量为相对轨道拟平根数，需要进行变量转换.记观测量为Z，则偏差为Δ=Z-HX.H矩阵中的-1.5［u*1(t1)-u*1(t0)］Δa表示目标星与跟随星之间由半长轴偏差时间积累导致的切向漂移线性化近似，u*1(t0)为编队导航初始时刻目标星的纬度幅角.取Δu*1=u*1(t1)-u*1(t0)代表的是目标星在轨道面内运动经历的弧度，为一个递增的值，不能简单地将其中的u*1(t1)理解为目标星当前时刻的纬度幅角.

在进行长期编队导航时，Δu*1与Δa的匹配存在问题，具体表现为Δu*1累积的时间越长，当前时刻计算-1.5［u*1(t1)-u*1(t0)］Δa使用的Δa越大，这使得乘积项-1.5［u*1(t1)-u*1(t0)］Δa不能准确体现半长轴偏差导致的切向漂移随时间变化的过程.

3 基于约化相对轨道拟平根数的编队导航方法

针对上述模型的线性化误差，设计基于约化相对轨道拟平根数的编队导航方法，其主要特点为:

(1)考虑半长轴偏差Δa对模型的影响，导航时不再对Δa进行滤波，直接由累积的切向漂移进行估计并用于状态预测;

(2)使用约化相对轨道拟平根数进行滤波，其中Δu为卫星之间纬度幅角平根的偏差.半长轴偏差造成的切向漂移已体现在公式(9)中a1Δu项，因此使用约化相对轨道拟平根数表述测量方程和测量矩阵显然更为合理.

3.1 相对轨道拟平根数的运动学方程及状态预测

导航算法的状态预测需要考虑半长轴偏差的影响，使用相对轨道拟平根数的运动方程，其形式如下［12-13］:

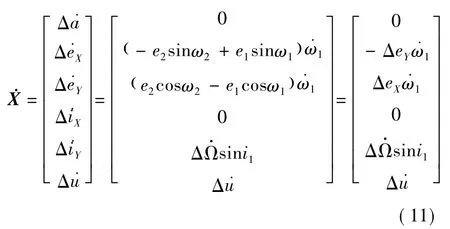
式中，

3.2 约化相对轨道拟平根数及其导航模型

约化相对轨道拟平根数定义为

测量矩阵定义为

测量方程满足

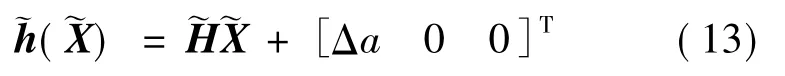
考虑到Δa的数值稳定性，Δa根据一段时间积累的切向漂移Δl结合公式Δl=-1.5ntΔa进行估算，其中n为轨道角速度.一般取经历一轨约6 000 s积累的Δl=l(t0+6 000)-l(t0)，l(t)的计算公式参见式(8).综上所述，半长轴偏差满足

3.3 扩展卡尔曼滤波

运行在近圆轨道上的编队卫星，当满足两星相对距离远小于轨道半长轴的假设，可以采用EKF进行导航滤波.EKF的标准算法如下［15-16］:

其中:Zk表示当前时刻观测量;表示前一时刻滤波状态量;表示由状态方程和RK4方法计算得到的状态预测量;的形式参见式(11);为测量矩阵，其形式参见式(12);表示的是测量方程，其形式参见式(13);Φk，k-1为状态矩阵，其形式参见式(14);Pk-1表示前一时刻状态误差协方差阵;Pk/k-1表示预测的当前时刻状态误差协方差阵;Q为系统状态噪声协方差矩阵;R为测量噪声协方差矩阵;Kk为当前时刻的卡尔曼增益矩阵.

4 数值实验

4.1 数值实验设计及仿真条件

考虑如下形式的SAR卫星编队工况:编队构型参数为p=388 m，s=3 060 m，θ=84°，φ=90°，l= 100 m，Δa=-1 m.GNSS接收机通过星间链路进行载波相位差分得到相对位置观测数据，测量精度为单轴0.1 m.目标星与跟随星的大气阻力摄动设置10%的偏差量.

4.2 仿真分析

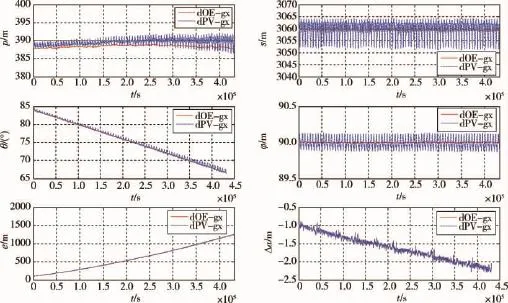
图2 两种不同的编队构型参数确定方法的比较Fig.2 Comparison of different formation determinations

根据上述条件仿真5天，得到仿真结果如下.图2为针对轨道动力学数据，两种不同编队构型参数确定方法的比较，由相对轨道拟平根数求得的构型参数稳定形更佳.图3为改进前后编队导航结果的比较，改进后的导航算法构型参数的准确精度更高且稳定性更好.

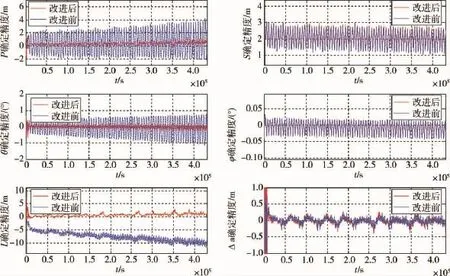
图3 改进前后编队导航结果的比较Fig.3 Comparison of navigation results between the improved approach and old approach

特别是改进后的算法克服了参数l确定精度的单向发散问题.改进前后的编队构型参数确定精度如表1所示.

表1 编队构型参数的确定精度Tab.1 Precision of formation feature determination

5 结论

本文介绍了一种基于星间相对测量与相对轨道拟平根数的卫星编队导航方法.文中指出，编队导航模型的线性化误差主要体现为半长轴偏差造成的切向漂移的状态预测与观测量不匹配.针对上述问题，本文提出了根据切向漂移进行半长轴偏差估计和针对约化相对轨道拟平根数进行导航滤波的编队导航方法.该导航方法对大气阻力造成的半长轴随时间累积的偏差具有良好的辨识能力，能够输出长期稳定的高精度编队导航结果.

参考文 献

［1］杨乐平，朱彦伟，黄涣.航天器相对运动轨迹规划与控制［M］.北京:国防工业出版社，2010.

［2］ALFRIEND K T，VADALI S R，GURFIL P，et al.Space formation flying:dynamic，control and navigation［M］.Elsevier，2009.

［3］林来兴，车汝才.卫星编队飞行精确动力学模型与三维定位系统［J］.宇航学报，2008，29(3):831-837.LIN L X，CHE R C.Accurate dynamics models of satellite formation flying and 3-dimension positioning system［J］.Journal of Astronautic，2008，29(3):831-837.

［4］杨维廉.基于轨道摄动解的卫星编队飞行［J］.宇航学报，2008，29(4):1166-1171.YANG W L.Formation flying based on orbit perturbation solution［J］.Journal of Astronautic，29(4):1166-1171.

［5］楚瑞.EKF/UKF在编队飞行卫星GPS相对导航中的应用［J］.空间控制技术与应用，2008，34(5):57-60.CHU R.Application of EKF/UKF in the GPS relative navigation for formation flying of spacecraft［J］.Aerospace Control and Application，2008，34(5):57-60.

［6］刘付成，完备，杜辉珂，郑科宇.近地轨道编队飞行卫星构形保持控制方法研究［J］.上海航天，2014，31 (4):6-10.LIU F C，WAN B，DU Y K，ZHENG K Y.Researchon satellites formation-keeping control method in low earth orbit［J］.Aerospace Shanghai，2014，31(4):6-10.

［7］Amico S D，Gill E，Montenbruck O.Relative orbit control design for the PRISMA formation flying mission［C］//Proceedings of the Conference of AIAA Guidance，Navigation and Control.Washingtong D.C.: AIAA，2006.

［8］GILL E，MONTENBRUCK O，AMICO S D.Autonomous formation flying for the PRISMA mission［J］.Journal of Spacecraft and Rockets，2006，44(3):671-681.

［9］杜耀珂，阳光，王文妍.InSAR卫星编队构型的e/i矢量设计方法［J］.上海航天，2011，28(5):8-13.DU Y K，YANG G，WANG W Y.e/i vector design method for InSAR formation flying orbit［J］.Aerospace Shanghai，2011，28(5):8-13.

［10］SIMONE D A，ARDAENS J S，LARSSON R.Spaceborne autonomous formation-flying experiment on the PRISMA mission［J］.Journal of Guidance，Control，and Dynamics，2012，35(3):834-850.

［11］涂佳，谷德峰，吴翊等.基于星载双频GPS的长基线卫星编队高精度快速星间相对定位［J］.系统工程与电子技术，2011，33(8):1850-1855.TU J，GU D F，WU Y，et al.Precise and rapid intersatellite relative positioning for long baseline satellite formation using onboard dual-frequency GPS［J］.Systems Engineering and Electronics，2011，33(8):1850-1855.

［12］刘林.航天器轨道理论［M］.北京:国防工业出版社，2000.

［13］OLIVER M，EBERHARD G.卫星轨道-模型、方法和应用［M］.王家松，祝开建，胡小工，等译.北京:国防工业出版社，2012.

［14］章仁为.卫星轨道姿态动力学与控制［M］.北京:北京航空航天大学出版社，1998.

［15］付梦印，邓志红，闫莉萍.Kalaman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003.

［16］杜耀珂，彭仁军.近地卫星利用光学敏感器的自主导航方法［J］.空间控制技术与应用，2008，34(4):55-59.DU Y K，PENG R J.Autonomous navigation for the near-earth satellite using the optical sensors［J］.Aerospace Control and Application，2008，34(4):55-59.

Long-Term Stable and High-Precision Relative Navigation Method for Satellites Formation Based on Reduced Relative Orbit Elements

YANG Shengqing1，2，DU Yaoke1，2，JIA Yansheng1，2，WANG Wenyan1，2
(1.Shanghai Institute of Spaceflight Control Technology，Shanghai 201109，China; 2.Shanghai Key Laboratory of Aerospace Intelligent Control Technology，Shanghai 201109，China)

Based on inter-satellite measurement and reduced relative orbit elements of satellites，an improved approach of formation navigation is investigated.The traditional navigation algorithm transforms the relative orbit elements into the relative position by measuring equations，which results in nonlinearity of the navigation model.In the improved approach，the difference of semi-axis is estimated via the excursion in along-track.The problem of linearization error can be solved by using the difference of semi-axis，which has an important influence on relative dynamic of satellites.The method can realize a long-term stable and high-precision navigation of satellites formation.

satellites formation;long-term stabilization;relative navigation;reduced relative orbit elements;difference of semi-axis

V474.1

A

1674-1579(2017)01-0030-06

10.3969/j.issn.1674-1579.2017.01.005

杨盛庆(1985—)，男，高级工程师，研究方向为卫星轨道动力学、卫星编队导航;杜耀珂(1982—)，男，高级工程师，研究方向为卫星编队导航与控制;贾艳胜(1983—)，男，工程师，研究方向为卫星编队导航;王文妍(1975—)，女，研究员，研究方向为卫星编队导航与控制.

*上海市青年科技启明星计划资助项目(17QB1401400).

2016-08-01