拟蛇算法在蛋白质折叠模拟中的应用可行性研究

张 菁，郭 丹,2

拟蛇算法在蛋白质折叠模拟中的应用可行性研究

张 菁1，郭 丹1,2

(1. 哈尔滨工程大学，计算机科学与技术学院，黑龙江 哈尔滨 150001；2. 哈尔滨商业大学，计算机与信息工程学院，黑龙江 哈尔滨 150028)

本文以计算分子生物学中的蛋白质折叠模拟为研究对象，通过对一种新算法的可行性研究，意旨为领域内的算法研究提供一种可验证性的算法。本文从收敛性和稳定性的角度，分析了拟蛇算法的核心函数，验证该算法在蛋白质折叠模拟中的应用具有全局最优值的收敛性，并且进一步研究了这种仿生算法的运动稳定性，验证了拟蛇算法的运动轨迹会达到一个稳定状态，这与蛋白质折叠最后形成能量最小的稳定状态的理论相吻合，验证结果表明，拟蛇算法在蛋白质折叠模拟中应用具有可行性。

拟蛇算法；蛋白质折叠；可行性研究；摆

0 引言

计算分子生物学[1]是运用计算机软件理论和技术，以分子生物学数据为研究对象的交叉研究领域。分子生物学的海量数据需要计算机学科的高效处理方法作为实验前数据预处理、数据筛选、数据预测，以及实验后的数据分析处理的重要技术支撑；另一方面，计算机对复杂大数据的处理研究，需要真实的有意义的训练数据集，分子生物学的迅速发展，产生了大量的数据，而其间的关系也日趋复杂，这些庞大的复杂数据集合正是一个好的算法研究的数据验证对象。

计算机模拟技术运用高速计算算法可以有效的对真实实验中的复杂大数据集进行分析和处理，并且通过对不同实验环境和实验因素的计算机模拟可控性，得到更多实验的可能性和更精确的理想化结论，也可以清晰的通过构象的变化来分析被模拟过程中哪些因素的影响格外重要，从而对功能关系的相互作用得出预测性的实验依据帮助研究人员理解。

蛋白质折叠是分子生物学上生物自我组织的一个典型实证。计算分子生物学中的蛋白质折叠模拟算法是一个重要的研究对象。通过氨基酸长链弯曲、扭曲和折叠，蛋白质可以在三维结构上具有不同的构象。结构生物学已经验证，蛋白质二维或三维结构决定了蛋白质的特定功能[2]。

目前人类对于折叠机制的了解程度还不足以精确的预测一个特定的序列如何折叠到天然构象，或用逆折叠方法设计出能折叠到具有稳定结构的真实蛋白的新序列[3]。虽然这种结构上的改变在自然界中只需要几秒到几分钟，但到目前为止，即便是速度最快的计算机也无法完成。

蛋白质由数目庞大的氨基酸组成，氨基酸不同结构的排列可能性，决定了蛋白质构象可能具有无穷种结构性状，这也就意味着模拟算法的机制尽可能的要接近真实折叠机制，在众多预测算法中，很多仿生预测算法应运而生，用自然界已知的生物具有的自身特征性算法去解决未知的生物问题，如人工鱼群算法[4,5]、遗传算法[6,7]、人工神经网络[8,9]、粒子群算法[10,11]、蚁群算法[12,13]等。拟蛇算法[14]是一种新颖的蛋白质折叠预测算法，本文对这一算法在蛋白质折叠模拟中的应用可行性进行研究，以推动该算法在领域研究中的运用。

1 拟蛇算法

自然界中，蛇不具有四肢，但它可以靠躯体的形状的改变来获得移动的动力。在这一点上，它与蛋白质无论从形状到运动形式都有相似的地方。在粗糙得地面上蛇作一连串的波浪状弯曲，体侧不断向地面施加压力，由于地表的反作用力关系，所以能推动蛇体向前前进。躯体较粗的蛇或接近猎物时，常常采取直线运动方式爬行。这类蛇的特点是腹鳞与其下方的组织之间较疏松，由于肋骨与腹鳞间的肋皮肌有节奏的收缩，使宽大的腹鳞依次竖立于地面，于是蛇体就能不停地呈直线向前运动。捕捉到猎物后，蛇会将自身盘紧促使猎物窒息死亡。蛇的运动具有运动稳定性好，适应地形环境能力强等特点。

其运动具有以下特点：1）能在凹凸不平的地面上移动，有良好的地形自适应性；2）适合于在沼泽、沙漠等松软环境中行进；3）能通过孔洞等狭小而又弯曲的通路，有较强的过障碍能力；4）能经常保持力学的稳定状态。

蛋白质折叠的结果也是趋于形成低能量的力学的稳定状态的物质。蛋白质的折叠过程经历了一个中间状态的，这种状态被科学家形容为熔球[15]。熔球不像正常折叠后结构紧密地蛋白那样脆弱，这样的结构可以进行拉扯，不会被轻易破坏。熔球具有正常蛋白所有的二级结构，但是这种二级结构尚未正确折叠形成更高级的结构。当蛋白质折叠成稳定构型时，其能量是最低的。蛇的运动与蛋白质折叠在形状和运动形式上有相似之处，因此研究和制作蛇形仿生算法来解决蛋白质折叠问题具有一定的研究可能性。

拟蛇算法作为一种仿生算法，主要以蛋白质折叠过程为研究对象，通过对蛇捕获猎物的过程模拟蛋白质折叠过程。以蛇的三种运动模式：波浪运动、直线式运动和盘绕运动，去模拟蛋白质折叠过程：折叠初期的波浪运动、折叠过程中短暂的直线式运动和折叠后期的盘绕运动。

对于蛇捕食过程的描述：在其未发现捕食目标前的觅食过程中蛇做波浪运动，通过随机探测目标的位置，即，当其与食物（外力）距离远时（折叠开始时），或当区域空间大，拥挤浓度低时，蛇的躯体作波浪运动，其从头部至尾部，形成若干个波峰和波谷，波峰和波谷随时间交替改变，肽链的移动路径是正弦波；一旦锁定捕食目标，进入攻击状态，即，当其与食物（外力）距离近时（折叠中期），其改波浪运动为直线移动以快速接近猎物，长的肽链的移动路径为直线式；当捕获食物后（折叠后期），其做盘绕运动，将猎物盘紧以稳定捕获状态，进而完成整个捕食过程，肽链的移动路径是螺旋曲线。

在蛋白质折叠模拟过程中拟蛇算法的实现步骤：1）初始状态：随机产生一条蛋白质序列的构型。给出氨基酸残基个数，设定肽链折叠的最大距离参数，更新速度步长，给肽链最小能量设初值；2）当折叠距离小于折叠的最大距离时，做波浪运动，并计算肽链总的最小能量值；3）当折叠距离等于折叠的最大距离时，做直线运动，并计算肽链总的最小能量值；4）当折叠距离大于折叠的最大距离时，做盘绕运动，并计算肽链总的最小能量值。5）肽链总的最小能量不再变化时，输出蛋白质构型，算法结束[16]。

拟蛇算法根据六个典型的蛋白质空间结构，在蛋白质折叠模拟过程中，通过改变参数演化两种函数形式，圆型和扣型两种类型。拟蛇算法的核心函数是：

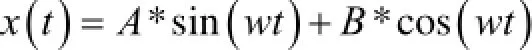
本文从收敛性和稳定性两个方面，通过对核心函数的分析，验证拟蛇在蛋白质折叠模拟中的应用可行性。

2 收敛性的分析

对于一种算法，其收敛性往往是人们所首要关心的问题。在拟蛇算法中，蛇的正弦移动行为奠定了算法收敛的基础，直线移动行为增强了算法收敛的稳定性和全局性，盘绕行为则增强了算法收敛的快速性和全局性，其行为过程也对算法收敛的速度和稳定性提供了保障。总的来说，算法中对各参数的取值范围还是很宽容的，并且对算法的初值也基本无要求。

拟蛇算法中残基个数，残基移动的最大速度和步长在迭代次数100时，这三个参数对算法收敛性的影响都是有限的，而合理选择迭代次数是提高算法效率的关键。这一规律是否具有一般性还有待进一步研究。

由于算法参数不同，收敛过程和结果也存在一定的差异，所以在以下的讨论中，将针对每一种参数连续多次进行全局寻优收敛实验作为一组数据，然后对多组数据进行统计分析，从而确定各参数的性质。通常数据的均值(Mean)表征本组数据的优劣，其标准误差(SE)则可以反映该组数据的稳定性。

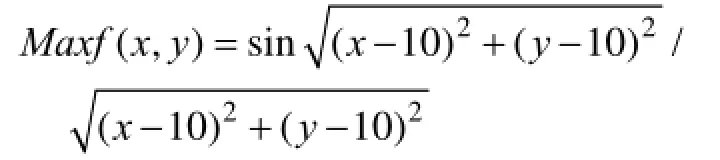
基于上面的二维正弦函数分析算法的收敛性，其中，0≤x≤20,0≤y≤20。该函数的全局极大值的周围被无穷个极小值(波谷)所包围，再外围是无穷个局部极大值(波峰)，在最远端的四个角上又是处于局部极大值。使用该函数作为实验函数应该具有一定的代表性。对于该函数，从拟蛇算法的任何初始值出发，都能收敛到全局最优值，并且收敛时间最短为几秒。

3 稳定性分析

拟蛇算法的核心是一种振荡形式[16]。一个理想的摆，力是Fkx=-，位置坐标x，质量为m。位置坐标可以表示为：x=x(t)，速度函数为v=v(t)。这两个函数彼此间有以下的关系：

方程式1定义速度函数，方程式2是牛顿定律用之于震荡的摆，对式2两边对t求导，然后将式1带入式2的求导，结果消去dx(t)/dt便得到一个二阶常系数线性微分方程，可以解出v(t)

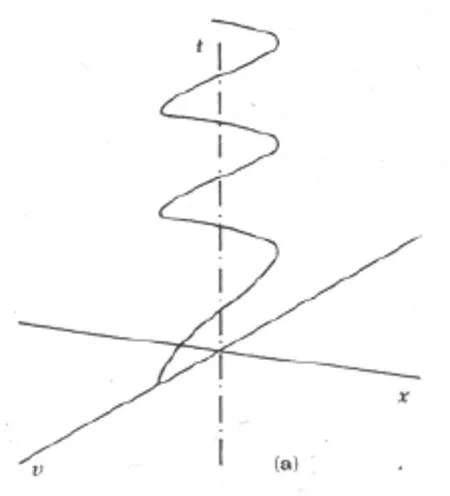
图1a 速度v随时间的t的变化Fig.1 a velocity change according to time

图1给出由公式4所给出的摆状态的时间演化图。这个摆既在时间上有位置的移动，又在时间上有速度的变化，所以这系统的点的轨迹是上升的螺旋线。

相轨线[12-14]的概念在有关耦合非线性微分方程的讨论中是很重要的，在缺乏完整分析一个动力学系统的情况下，摆的相轨线可用于有关运动本质的稳定性的分析。

相轨线是三维螺旋在v-x平面上的投影。也就是说我们要构造一个函数v=v(x)。这可以由公式5，6消去时间而做到。

所以我们可以得到：

对给出的初始条件来说，或者等价地说，对一个固定值K，公式（7）代表v-x平面上的一个椭圆如图2所示。每一个K值，有一个椭圆与之对应。

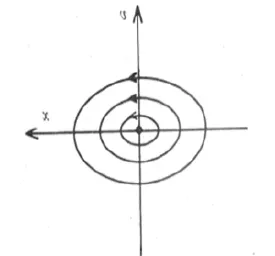
图2 一个理想摆在相平面上的轨迹Fig.2 An idea Gradual stable focus

当相平面轨线的螺旋线趋向于奇点，如图3，从而这个奇点叫做稳定焦点。在这种情况下，总的解趋向于一种振荡运动中的定态，是渐近稳定的。

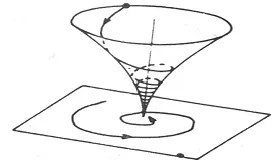
图3 渐近稳定焦点，螺旋轨迹收敛于奇点Fig.3 Gradually to stable focus, screw track to odd spot

理想状态下，拟蛇算法的核心函数在振荡模型下，摆的特征方程：

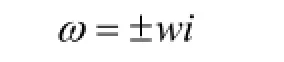
即iωω=±虚

摆有两个纯虚根，并且有，摆反映在坐标x与v上的代表点在相平面上随时间而作周期的变化。因此，其相轨迹线必然都是一些围绕奇点的封闭曲线。

摆是在小的瞬时的位移x=δx，摆就开始摇动，而此运动是x=x(t)与v=v(t)随时间而减少，并最后为零，则摆的位置x=0，v=0,是一个稳定的状态，我们把这一点叫做稳定奇点。

对于施加在摆上的每个初始力，会出现一条新的封闭的相轨线，如图2所示。一个理想的摆可以规律性地振荡着，只要没有新的扰动去干扰它的运动，此时的奇点是稳定的。摆运动轨迹的稳定性恰好与蛋白质折叠最后形成能量最小的稳定状态的理论相吻合。

4 结论

本文针对蛋白质折叠模拟研究中一种新算法的可行性研究，对拟蛇算法的核心函数进行了收敛性和稳定性分析。通过对算法收敛性的分析，以迭代次数100为限制，验证该算法核心函数从任意初始值出发，都能收敛到全局最优值，并具有较快收敛速度，能有效地对蛋白质折叠进行模拟预测。通过对算法稳定性分析，从振荡理论的摆轨迹的相平面稳定性研究，验证了在理想状态下拟蛇算法的运动轨迹在能达到一个稳定状态，这与蛋白质折叠最后形成能量最小的稳定状态的理论相吻合。拟蛇算法仅使用了目标问题的函数值，算法简单，具有很强的跳出局部极值的能力，算法的稳定性确保其能快速跟踪随着工作状况或其他因素的变更造成的极值点的漂移变化，获得全局最优解。综上所述，拟蛇算法在蛋白质折叠模拟研究中，具有应用可行性。

[1] ZHANG Y, Min X J. Computational molecular biology: an integration of experimental molecular and genome biology with computational technology: computational molecular biology[J]. 2011, 1(1): 1-3.

[2] GEORGINA M, DANCO D. Incorporating several features in the protein ray descriptor for more accurate protein 3D structure retrieval: Proceedings of the ACM workshop on 3Dobject retrieval [C]. 2012, 51-56.

[3] SCHAEFFER R D, DAGGETT V. Protein folds and protein folding: protein engineering design & selection[J]. 2011, 24(1-2): 11-19.

[4] CUI Z H, ZHANG Y. Swarm Intelligence in Bioinformatics: methods and implementations for discovering patterns of multiple sequences: journal of nanoscience and nanotechnology[J]. 2014, 14(2): 1746-1757.

[5] CUI Z H, ZHANG Y. Methods and implementations for discovering patterns of multiple sequences: journal of nanoscience and nanotechnology[J]. 2014, 14(2): 1746-1757.

[6] ISLAM M L, SHATABDA S, RAHMAN M S. GreMuTRRR: A novel genetic algorithm to solve distance geometry problem for protein structures: 2014 international conference on electrical and computer engineering (ICECE)[C]. 2014, 357-360.

[7] SHIN JM, LEE B, CHO KH. A new efficient conformational search method for ab initio protein folding study: window growth evolutionary algorithm: bulletin of the Korean chemical society[J]. 2016, 37(12) 1971-1976

[8] FLORIDO J P, POMARES H, ROJAS I. Prediction of functional associations between proteins by means of a cost-sensitive artificial neural network: lecture notes in computer science[J]. 2011, 6692: 194-201.

[9] THANGSUNAN P, KITTIWACHANA S, MEEPOWPAN P, KUNGWAN N, PRANGKIO P, HANNONGBUA S, SUREE N. Rapid activity prediction of HIV-1 integrase inhibitors: harnessing docking energetic components for empirical scoring by chemometric and artificial neural network approaches: journal of computer-aided molecular design [J]. 2016, 30(6): 471-488.

[10] KONDOV I. Protein structure prediction using distributed parallel particle swarm optimization : natural computing [J]. 2013, 12(1): 29-41.

[11] CHEUNG N J, DING X M,SHEN H B. Protein folds recognized by an intelligent predictor based-on evolutionary end structural information :journal of computational chemistry. 2016, 37(4): 426-436.

[12] OAKLEY M T,RICHARDSON E G, CARR H. Protein structure optimization with a "lamarckian" ant colony algorithm: IEEE-ACM transactions on computational biology and bioinformatics[C]. 2013, 10(6): 1548-1552.

[13] RAY S S,PAL S K. RNA Secondary structure prediction using soft computing: IEEE-ACM transactions on computational biology and bioinformatics[C]. 2013, 10(1): 2-17.

[14] 张天驰, 张菁. 模拟蛋白质折叠过程的新算法研究. 生物信息学[J]. 2011, 9(31): 142-145.

[15] https://en.wikipedia.org/wiki/Molten_globule

[16] 张菁, 张天驰. 蛋白质折叠过程模型. 应用科技[J]. 2011, 38(7): 41-43.

Application Feasibility Study on Snake Algorithm of Protein Folding Simulation

ZHANG Jing1, GUO Dan2
(1. Harbin Engineering University, College of Computer Science and Technology, Heilongjiang Harbin 150001, China; 2. Harbin University of Commerce, School of Computer and Information Engineering, Heilongjiang Harbin 150028, China)

The research object of the paper is a new simulation algorithm for protein folding in computational molecular biology. From the view of the astringency and stability, the algorithm research in the field of the purpose of this paper is to provide a kind of algorithm of verifiability. In this paper, snake algorithm was validated is accord with the global optimum of the astringency in the application of protein folding simulation by analyses the core function. And the project further studies the movement stability of the bionic algorithm. Proved that the proposed algorithm of snake trajectory will reach a steady state, which was consistent with Minimum energy of the formation of stable state theory when protein folding is complete. Results show that the proposed snake algorithm was feasible for application in the numerical simulation of protein folding.

Snake algorithm; Protein folding; Feasibility study; Pendulum

TP39 3.08

A

10.3969/j.issn.1003-6970.2017.02.017

黑龙江省教育厅科学技术研究基金项目(12541211)

张菁(1965-)，女，博士后，教授，博士生导师，研究方向为计算分子生物学，虚拟现实，医学图像处理；郭丹(1978-)，女，博士研究生，副教授，研究方向为计算分子生物学，大数据可视化。

本文著录格式：张菁，郭丹. 拟蛇算法在蛋白质折叠模拟中的应用可行性研究[J]. 软件，2017，38（2）：75-79