一种数值积分算法的改进研究

吴佳惠

一种数值积分算法的改进研究

吴佳惠

(新疆大学 电气工程学院，新疆乌鲁木齐 830047)

本文分析了Matlab软件常用的常系数微分方程的数值积分算法和含有间断特性的微分方程求解方法，重点研究了ODE45算法，并针对其求解不连续问题有可能出现误差，采用条件函数零点搜索法进行了改进，通过用ode45，ode23，ode113，ode15s，ode23s，ode23t和ode23tb求解器求解算例和本文用改进的ODE算法求解算例比较，验证了本文改进算法的有效性和适用性。

数值积分；微分方程；ODE45

0 引言

物理学、机械学、电学和热力学的基本定律通常都是建立在经验性的观测资料之上的，这些观测资料可以解释物理性质和系统状态变化，定律一般不直接描述物理系统的状态，而是通过时间和空间的变化来表达。这些定律定义了变化的机制，一旦与能量、质量或动量等连续性定律结合，就得到了常微分方程[1]。数值积分是求解这类方程非常重要而常用的数值计算方，也是在实际中得到广泛应用的算法[9]。

Matlab软件中一般含有ode45(Ordinary Difference Equation, ODE)，ode23，ode113，ode15s，ode23s，ode23t和ode23tb求解器，ode45是四/五阶龙格-库塔法，适用于大多数连续或离散系统，但不适用于刚性（stiff）系统；ode23是二/三阶龙格-库塔法；ode113是一种阶数可变的解法器；ode113是一种多步解法器；ode113是变阶Adams法；ode15s：是一种基于数字微分公式的解法器；ode23s是一种单步解法器；ode23s是定阶单步法；ode23t是梯形规则的一种自由插值实现；ode23tb是具有两个阶段的隐式龙格-库塔公式。在这些公式中ode45应用最广泛[7][10]，但是，函数的连续性对保证计算精度是十分重要的，单步法要求在一个步长内右端函数连续，K阶多步法则要求在K步内右端函数连续，但是在实际问题中经常遇到不连续的情况，条件函数零点搜索法解决具有一般间断特性时的求解方法[2]。若能事先确定满足条件函数的点，然后就可以恰当地选择步长。根据条件函数的特点，若条件函数仅与时间有关，事先确定满足条件函数的时间点值，计算推进时，每一步均与间断点时间值进行比较，使当前步不跨过间断点[2]。

国内很多学者针对各种情况研究了数值积分算法，取得了大量可以借鉴的成果[3-6][8]。本文针对matlab软件中常用的ODE45算法进行改进研究，采用件函数零点搜索法与ODE45算法结合，可以有效求解含有间断特性的常微分方程问题。

1 RKF45算法改进

RKF（Runge–Kutta–Fehlberg）45即4阶5级龙格-库塔-费尔别格法，也matlab软件中ODE45算法，具体表达式如下：

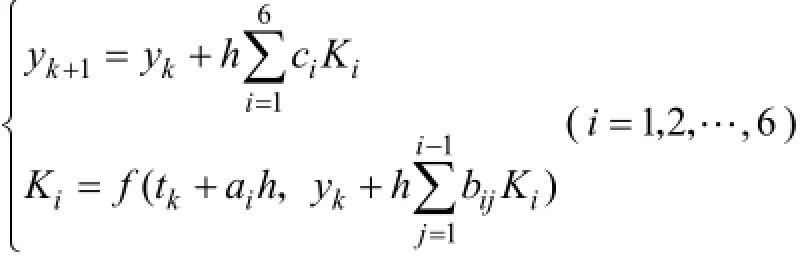
式中的各系数见表1。

主要软件代码为：

while (tout(i)＜=tend)

tout(i+1)=tout(i)+h;

k1=f(yout(i));

k2=f(yout(i)+h*k1*1/4);

k3=f(yout(i)+h*(k1*3/32+k2*9/32));

k4=f(yout(i)+h*(k1*1932/2197–k2*7200/21 97+k3*7296/2197));

k5=f(yout(i)+h*(k1*439/216–k2*8+k3*368 0/513–k4*845/4104));

k6=f(yout(i)+h*(–k1*8/27+k2*2–k3*3544/2 565+k4*1859/4104–k5*11/40));

yout(i+1)=yout(i)+h*(k1*25/216+k2*1408/2565 +k4*2197/4104–k5*1/5);

y_hat=yout(i)+h*(k1*16/135+k3*6656/12825+k 4*28561/56430–k5*9/50+k6*2/55);

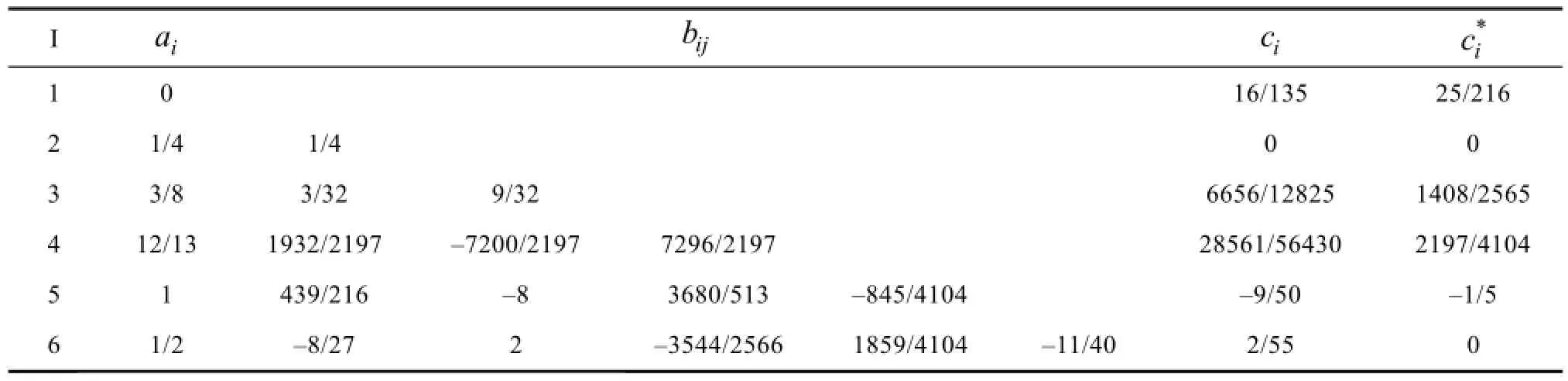
表1 Fehlberg公式中的各系数Tab.1 The Coefficients in Fehlberg Formula

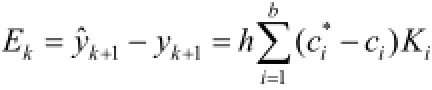
由文献[2]可知，当用经典的数值积分法（包括单步法和多步法）进行数值求解时，右端函数的连续性对保证仿真精度是十分重要的。单步法要求在一个步长内右端函数连续，K阶多步法则要求在K步内右端函数连续，为了使仿真结果达到一定精度，人们往往采用变步长方法。然而，采用变步长方法也会遇到困难。

由文献[2]可知，具有一般间断特性时的微分方程数值求解问题。若系统微分方程y˙=f(y,t)中右端函数f(y,t)不连续，不失一般性，可用以下形式来描述

即右端函数的表达式依赖于条件函数的取值。对上式所描述的系统，若能事先确定f(y,t)满足条件函数的点，即满足φi(y,t)=0的t*，然后就可以恰当地选择步长。根据条件函数的特点，条件函数若仅与时间有关，即φi(y,t)=φ(t)=0；事先确定满足条件函数的时间点值，数值求解推进时，每一步均与间断点时间值进行比较，使当前步不跨过间断点，这就是条件函数零点搜索法。

在经典RKF45算法中加入条件函数零点搜索法，可以使其更好地求解某些含有间断点的微分方程求解问题，其代码为：

if ((yout(i+1)＞=yhigh)&(yout(i+1)＞yout(i)))

if (yout(i+1) – yhigh ＞ tol)

h = h *(yhigh–yout(i))/(yout(i+1) –yout(i));

continue;

end

siphon=1;

elseif(yout(i+1)＜=ylow&(yout(i+1)＜yout(i)))

if (ylow–yout(i+1) ＞ tol)

h = h *(yout(i)–ylow)/(yout(i) –yout(i+1));

continue;

end

siphon=0;

end

2 案例验证

本文案例来自文献[1]，有一座间歇式喷泉，如图1。水以固定的流率Qin注入圆柱形容器，水位达到yhigh时容器被注满。这时候，水通过圆形排出管被虹吸出容器，在管子的尽头形成喷泉。喷泉一直喷射到水位线降至ylow，此时虹吸管中装满了空气，于是喷泉停止喷射。然后重复这个过程，当水位线到达yhigh，即容器被注满时，喷泉又开始喷射。当喷泉喷射时，根据托里切利定律（Torricelli’s law）,流出物Qout可以由下面的公式计算，

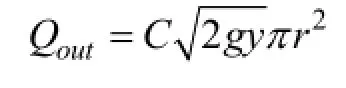
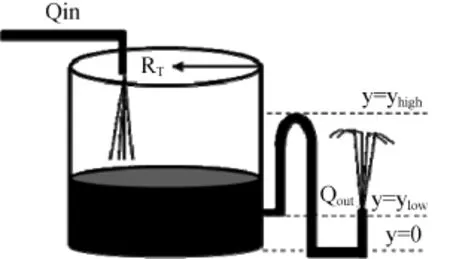
图1 间歇式喷泉Fig.1 Intermittent Fountain

忽略管中水的体积，计算100 s的时间内容器水位线与时间的函数关系并绘制图形，假设空容器的初始条件为y(0)=0，计算时使用下面的参数RT=0.05 m，r=0.007 m，ylow=0.025 m，yhigh=0.1，C=0.6，g=9.81 m/s2，Qin=50x10–6 m3/s。通过ode23，ode113，ode15 s，ode23 s，ode23 t和ode23 tb来求解结果如下图所示。图的结果明显是不正确的，除了最初的注满周期之外，水位线看起来在再次达到yhigh以前就开始下降。类似地，在排水的时候，水位线还没有降至ylow，虹吸管就关上了。

[1]可知，当喷泉喷射时，容器体积V(m3)的变化率由流入减去流出大的简单平衡确定

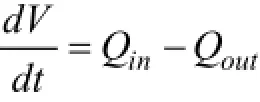
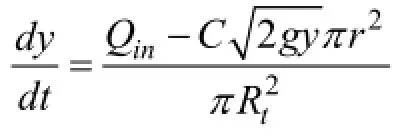
当喷泉停止喷射时，分子的第二项变成0。为此，我们可以在方程中加入一个新的无量纲的变量siphon，当喷泉停止时siphon等于0，当喷泉工作时siphon等于1。

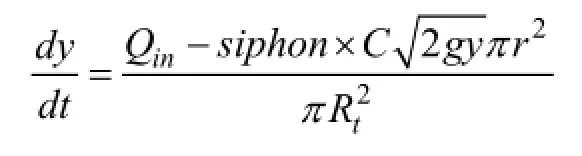
siphon可以被看成是控制喷泉停止和工作的开关。这种只具有两种状态的量被称为布尔变量或者逻辑变量，其中，0相当于假，1相当于真；将siphon与应变量y联系起来。首先，当水位线低于ylow时令siphon等于0。相应地，当水位线高于yhigh时令siphon等于1，下面的M文件函数在计算导数时考虑了这个逻辑关系。

Function dy=plinyode(t,y)

Global siphon

Rt=0.05; r=0.007; yhi=0.1; ylo=0.025

C=0.6; g=9.81; Qin=0.00005;

if y(1)＜=ylo; siphon=0;

elseif y(1)＞=yhi

siphon=1;

end

Qout=siphon*Csqrt(2*g*y(1))*pi*r^2;

Dy=(Qin-Qout)/(pi*Rt^2);

由于siphon的取值必须在函数调用之间被保持，所以它被申明为一个全局变量。虽然，我们不鼓励使用全局变量（特别是对于大型的程序），但是，它在当前的问题中很有用。下面的脚本用内置ode45函数积分Plinyode，并绘制解的图形。

global siphon

siphon=0;

tspan=[0 100]; y0=0;

[tp,yp]=ode113(@plinyode, tspan, y0);

plot(tp, yp);

xlabel(‘time, (s)’) ;

ylabel(‘water level in tank, (m)’)

[tp,yp]=ode15s(@plinyode, tspan, y0);

plot(tp, yp);

xlabel(‘time, (s)’) ;

ylabel(‘water level in tank, (m)’)

[tp, yp]=ode23(@plinyode, tspan, y0);

plot(tp, yp);

xlabel(‘time, (s)’);

ylabel(‘water level in tank, (m)’)

[tp, yp]=ode23s(@plinyode, tspan, y0);

plot(tp, yp);

xlabel(‘time, (s)’);

ylabel(‘water level in tank, (m)’);

[tp, yp]=ode23t(@plinyode, tspan, y0);

plot(tp, yp) ;

xlabel(‘time,(s)’);

ylabel(‘water level in tank, (m)’);

[tp, yp]=ode23tb(@plinyode, tspan, y0);

plot(tp, yp);

xlabel(‘time, (s)’);

ylabel(‘water level in tank, (m)’);

图的结果明显是不正确的。除了最初的注满周期之外，水位线看起来在再次达到yhigh以前就开始下降。类似地，在排水的时候，水位线还没有降至ylow，虹吸管就关上了。

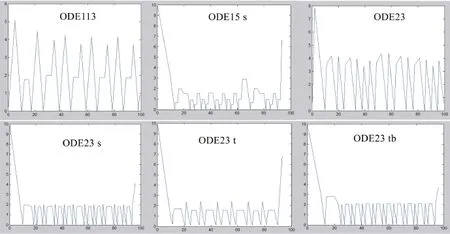
图2 Matlab软件中ODE求解算法求解的结果Fig.2 The results of ode algorithm in MATLAB software

由文献[1]可知，是因为ode在虹吸管开关时并不连续，例如，当容器注水时，导数仅仅依赖于固定的流入物和取值恒为某个参数。然而，一旦水位线到达yhigh，流出开关导通，导数迅速地变为另一个值，虽然Matlab所用的自适应步长程序对于许多问题微分方程求解问题十分有效，但是，它们在处理这类间断问题时往往会失效。我们用ODE45和改进的ODE45算法求解的结果如下，可以看出ODE45同样出现这种困难，是因为ODE在虹吸管开关时并不连续，但是采用改进的ODE45算法，就没有出现问题。因为，通过改进经典ODE45算法，加入了条件函数零点搜索法，所以，使得ODE45算法可以求解某些含有间断特性的微分方程求解问题。

图3 ODE45和改进的ODE45求解结果Fig.3 Ode45 and improved ode45 solution results

3 结论

本文分析了Matlab软件中一般含有ode45(Ordinary Difference Equation, ODE)，ode23，ode113，ode15s，ode23s，ode23t和ode23tb求解器，重点分析了ode45即龙格-库塔-费尔别格法。针对matlab软件中常用的ODE45算法求解含有间断特性的常微分方程会出现困难情况，采用件函数零点搜索法对ODE45算法进行了改进，通过算例验证了本文改进算法可以有效求解某些含有间断特性的常微分方程问题。

参考文献

[1] (美)Steven C.Chapra著; 唐玲燕, 田尊华译.工程与科学数值方法的matlab实现[Z]. 北京: 清华大学出版社, 2009, 5.

[2] 肖田元, 范文慧. 计算机仿真(第2版)[Z]. 北京: 清华大学出版社, 2010, 2.

[3] 杨录峰, 马宁, 赵双锁. 一种变步长和变阶计算的自适应数值积分算法[J]. 云南民族大学学报(自然科学版), 2011, 01.

[4] 张明会, 高婷婷. 一个数值积分公式的推广[J]. 四川文理学院学报, 2011, 02.

[5] 许江浩, 陈志坤, 刘斌. 一个高精度数值积分公式[J]. 四川理工学院学报(自然科学版), 2011, 02.

[6] 邢诚, 王建强, 贾志强. 多种数值积分方法比较分析[J].城市勘测, 2010, 01.

[7] 陈佩宁, 刘竞. 用MATLAB求数值积分的方法[J]. 石家庄职业技术学院学报, 2008, 06.

[8] 龙爱芳, 胡军浩. 一个新的数值积分公式[J]. 数学理论与应用, 2010, 04.

[9] 李海合, 王三福. 数值积分的一种改进方法[J]. 甘肃联合大学学报(自然科学版), 2009, 04.

[10] 张志涌等. 精通MATLAB6.5版(第1版)[Z]. 北京: 北京航空航天大学出版社, 2003.

Research on Improvement of a Numerical Integration Algorithm

WU Jia-hui
(College of Electronic Engineering, Xinjiang University, Urumqi 830047, China)

This paper analyzes the numerical integration algorithm of constant coefficient differential equation in MATLAB software, and solution method of differential equation with discontinuous characteristics. It focuses on the ode45 algorithm, and the error of solving the discontinuous problems, improves the zero search algorithm of conditional function, and verifies the effectiveness and applicability of the improved algorithm by comparing the results of using ode45, ode23, ode113, ode15s, ode23s, ode23t and ode23tb to solve the example with the results of using the improved ode algorithm to solve the example.

Numerical integration; Differential equation; Ode45

TP391.41

: A

10.3969/j.issn.1003-6970.2017.02.007

国家自然科学基金项目(51575469)

一种数值积分算法的改进研究

本文著录格式：吴佳惠. 一种数值积分算法的改进研究[J]. 软件，2017，38（2）：28-32