模糊C均值聚类算法的有效性检验研究

刘来权，陈 燕，雷燕瑞

模糊C均值聚类算法的有效性检验研究

刘来权，陈 燕，雷燕瑞

(海南软件职业技术学院，海南 琼海 571400)

模糊C均值（Fuzzy C-means，FCM）聚类算法是聚类算法中的经典算法，此算法引入了隶属度及模糊度的概念，应用范围及应用行业也更为广泛。FCM聚类算法的聚类划分受到数据分布的影响较大，模糊度参数的选择很容易影响聚类算法的聚类结果，且易陷入局部极值的问题。因此研究FCM聚类算法的有效性检验方法则具有非常意义。

模糊C均值；聚类；有效性；检验

0 引言

随着信息化技术的发展，各方收集的数据也随之呈级数级增加，数据已经在我们的日常生活中无处不在，国际数据公司（IDC）预测2020年全球将拥有35ZB（35*10亿TB）的数据[1]，如果靠人工的方式处理这些数据显然不现实，聚类则是进行数据挖掘中常用的数据分析方法[2]，数据的聚类算法研究也一直是一个非常重要的研究内容。

传统的聚类算法严格将划分对象归属于某一类，划分界限泾渭分明，具有“非此即彼”的特点[3]。而现实世界中的有些对象无法进行这么明显的划分，更适合按照特征进行隶属度的划分。1965年，美国的数学家L.A.Zadeh发表了《模糊集（Fuzzy Sets）》，第一次将模糊性与数学联系在一起[4]。以此为起点，有科学家不断将模糊划分的概念应用于数据挖掘中，人们开始用模糊的划分方法来处理聚类问题，因模糊划分的中介性，能更加客观的反应现实世界的问题，因此成为研究的主流方向[5]，目前也是最广泛应用的聚类算法之一。

模糊聚类算法属于无监督的算法，一般用于分类算法的评价方法不适合评价模糊聚类算法。目前，有关聚类有效性检验的研究也有很多。

1 模糊C均值聚类算法

对于一个包含n个样本的数据集合X=｛x1,x2……,xn｝，样本xk∈X,k=1,2,……,n 。聚类过程将其划分为c类，得到划分矩阵U(X)，用U=■uik■c*n则表示样本对类别的隶属度矩阵，uik则

模糊C-均值聚类算法的基本思想是：表示的是数据集合X的第k个样本数据xk对第i类的隶属度，V=｛vi｝,i=1,2,……,c 则表示的是各个类别的聚类中心[6]。FCM算法定义数据集合X中样本与聚类中心的误差平方为[7]：

Dunn对每个样本点跟每个聚类中心的距离用隶属度平方加权，得到聚类内的加权平方和目标函数：

2 模糊聚类有效性检验

聚类算法是没有先行经验的算法，当确定聚类算法的选择之后，那么对于数据集该划分为多少类较为合理，对聚类的结果又该如何评价其优劣性，这就是聚类的有效性问题。虽然在一些应用中，聚类数可以通过用户的经验和领域知识进行估计，但一般情况下，聚类数是无法预先知道的，评价聚类质量并确定最佳聚类数是一项困难的工作。

聚类算法是没有先行经验的算法，因此待聚类的数据对象没有任何相关的属性标签，因此对于聚类结果的优劣性是没有办法直观评价的。聚类时对于同一种聚类算法，也会因出示聚类中心的选取以及聚类数目的设置不同，而产生不同的聚类结果。因此，评价聚类算法的划分结果并非易事，那么研究聚类的有效性检验问题就是非常关键的一步。

对于聚类算法的有效性研究，可以将其分为三类，第一类是仅考虑数据集集合结构信息的聚类有效性指标、第二类是仅考虑隶属度的聚类有效性指

标，第三类是仅考虑隶属度的聚类有效性指标、第四类是同时考虑数据集集合结构信息和隶属度的聚类有效性指标。由于待聚类数据的多样性特点，单一的评价方式不可能解决不同情况的聚类有效性问题，本文介绍给予几何结构的聚类有效性指标。

2.11991年Xie-Beni提出的有效性指标xieV[9]

其定义如下：

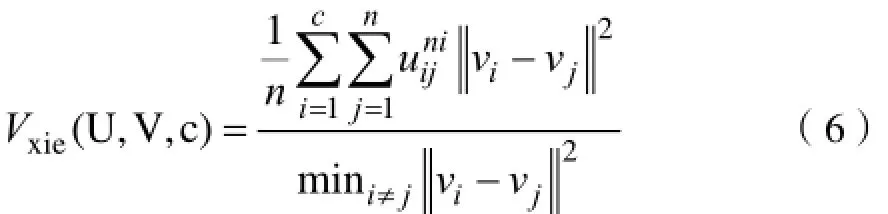
Vxie是聚类后类内部紧凑度以及类和类之间离散度的比例，公式(6)的分子用来衡量类内部的紧凑度，此值小则紧凑度高。Vxie(U,V,c)则是在类内部的紧凑度与类和类之间的分离度之间寻求一个平衡点，如果聚类可以使其值达到最小，则能够获得较好的聚类效果。

2.22011年Zalik K. R.和Zalik B. 提出的有效性指标SV指标[10]

SV指标不同于xieV，它使用最邻近的距离估计聚类的离散性，用边界点到每个类的聚类中心的距离表示类和类之间的紧致性。SV指标定义如下：

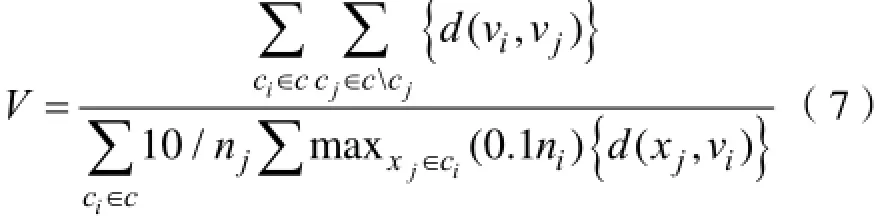
Zalik K.R.和Zalik B.随后提出了SV指标的模糊表达，用于模糊聚类的有效性检验。

关于聚类的有效性指标，有很多学者提出的各种指标，比如还有2001年Halkidi和Vazirgiannisp[11]提出的S_Dbw指标，2006年杨善林[12]提出的距离代价函数等。

3 小结

聚类是数据挖掘和人工智能方面使用非常广泛的方法之一，而聚类的目标是尽可能使得同一类内部紧致，而类和类之间尽可能离散。模糊聚类算法则同时使用模糊度和隶属度的方法，可使得聚类的样本同时隶属于两个或多个类，很大程度增强了模糊聚类的使用范围。虽然模糊聚类算法应用范围广，应用领域也多，但如何评估模糊聚类的有效性也是需要解决的问题。

[1] Gantz J, Reinsel D.Extracting value from chaos[J]. IDCiView, 2011: 1-12.

[2] 朴尚哲. 模糊C均值算法的聚类有效性评价[J]. 模式识别与人工智能, 2015(5): 452-461.

[3] 谢桂林, 詹志强, 李凯. 基于聚类的因子分解机推荐算法研究[J]. 软件, 2016(10): 113-117.

[4] Zadeh L A. Fuzzy sets[J]. Information and Control, 8(1965): 338-353.

[5] 孔攀. 模糊聚类分析及其有效性研究[D]. 西南大学. 重庆: 8-10.

[6] 杜淑颖. 基于大型数据集的聚类算法研究[J]. 软件, 2016, (01): 132-135+138.

[7] Dunn J C．A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well Separated Clusters[J]. Journal of Cybernetics, 1974, 3(3): 32-57.

[8] Pal N R, Bezdek J C. On Cluster Validity for the Fuzzy C-means Model. IEEE Trans on Fuzzy Systems, 1995, 3(3): 370-379.

[9] Xie X L. Beni G.A validity meansure for fuzzy clustering [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1992. 16(9): 954-960.

[10] Zalik K. R., Zalik B. Validity index for clusters of different sizes and densities[J]. Pattern Recognition Letters, 2011, 32(2): 221-234.

[11] Halkidi M., Vazirgiannis M.Clustering validity assessment: Finding the optimal partitioning of a data set[C]. IEEE International Conference on Data Mining(ICDM), 2001: 187-194.

[12] 杨善林, 李永森. K-means算法中的k值优化问题研究[J].系统工程理论与实践, 2006, 26(2): 97-101.

Research on the Validity of Fuzzy C Mean Clustering Algorithm

LIU Lai-quan, CHEN Yan, LEI Yan-rui
(Hainan College of Software Technology, Qionghai 571400, China)

Fuzzy C-means (FCM) clustering algorithm is a classical algorithm in the clustering algorithm, this algorithm introduces the concept of membership and fuzzy degree, the scope of application and the application of the industry is also more extensive C-means. The clustering of FCM clustering algorithm has a great influence on the data distribution, and the selection of fuzzy parameters can easily affect the clustering results of clustering algorithm, and it is easy to fall into the local extremum problem. Therefore, it is of great significance to study the validity of FCM clustering algorithm.

FCM; Clustering; Validity; Test

TP3-0

A

10.3969/j.issn.1003-6970.2017.02.004

海南省自然科学基金(No.20156232)资助

刘来权(1979-)，男，副教授，主要研究方向：项目管理、算法、多媒体应用；陈燕(1978-)，女，讲师，主要研究方向：多媒体应用，算法等；雷燕瑞(1980-)，女，副教授，主要研究方向：算法、数据库应用、程序开发、职业教育。

本文著录格式刘来权，陈燕，雷燕瑞. 模糊C均值聚类算法的有效性检验研究[J]. 软件，2017，38（2）：16-18