基于八邻域的自适应P-Laplace图像修复算法

张 波，徐黎明

(西华师范大学 计算机学院，四川 南充 637009)

基于八邻域的自适应P-Laplace图像修复算法

张 波，徐黎明

(西华师范大学 计算机学院，四川 南充 637009)

针对传统的变分图像修复算法仅仅利用四邻域信息导致的图像过渡不自然、人工干预强等问题，提出一种基于八邻域的自适应P-Laplace修复算法。该算法将待修复像素点的八邻域分为两组四邻域，利用每组四邻域信息，采用中心格式差分方法对待修复像素点进行处理，通过自适应方法确定每组邻域修复的最佳p值，最后再进行加权平均。仿真实验显示，该算法与近几年提出的修复算法相比图像评价较好，PSNR值提高了约5.74%～22.15%，TSSIM值提高约4～30个百分点。

变分图像修复；邻域；P-Laplace；自适应；图像评价

0 引言

图像修复[1]是一种在受损图像上对信息缺失或错误的部分按照特定的规律进行修复以恢复原图像的技术。现阶段图像修复技术主要分为3种：基于变分偏微分方程、基于纹理合成和基于图像分解的修复技术。在基于变分偏微分方程的算法中，以Chan等[2]提出的全变分(Total Variation,TV)算法、Bertamlio等[3]提出的BSCB (Bertamlio Sapiro Caselles Ballester)模型和曲率驱动扩散修复算法[4](Curvature Driven Diffusions,CDD)为典型。针对TV模型因较强的正则化约束引起的梯度效应和假边缘信息，文献[5]、[6]提出了改进的TV算法，较好地避免了梯度效应和假边缘情况。针对CDD算法耗时、容易引起模糊等问题，文献[7]提出的自适应CDD修复算法和文献[8]提出的基于模糊C-均值的自适应TV算法较好地克服了该问题。

文献[9]提出的基于压缩感知的改进TV模型在去噪的同时保护好了纹理和边缘信息，与基于纹理合成等其它算法[10～11]结合使用，增强了图像修复的应用范围。基于高阶扩散的修复算法[12～13]因其良好的扩散特性，使修复图像具有良好的视觉效果，但对图像特征要求高，修复时间较长。

上述几种变分偏微分算法相似之处在于将待修复像素点的四邻域信息作为已知信息，然后采用中心格式差分或半点格式差分的方法进行数值实现。对此，本文提出一种基于八邻域的自适应P-Laplace图像修复方法，充分利用待修复像素点的八邻域内的信息进行修复。

1 P-Laplace修复算法

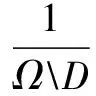
根据Rudin等提出的TV算法，利用拉格朗日乘子法能将约束性问题转化为无约束问题，得到变分修补模型的一般形式为：

(1)

文献[15]选取r(|▽u|)=|▽u|p，得到P-Laplace修复模型。该模型的定义为：

(2)

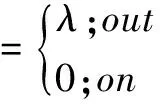
根据变分原理可以得到P-Laplace模型的Euler-Lagrange方程为：

(3)

在半点网格示意图(见图1)中利用半点格式差分法[16]求解式(3)。设目标像素为O(i,j)，其四邻域为：Q∈Λ={E,N,W,S}，e、n、w、s表示相应的半点像素，其四邻域为：q∈α={e,n,w,s}。

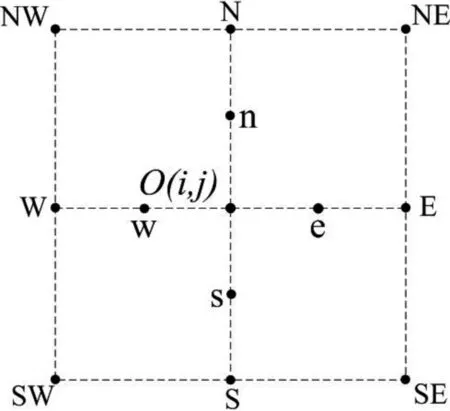
图1 半点网格示意图

对图像进行等间隔采样，步长h=1。令：V=(v1,v2)=|▽u|p-2▽u。divV由差分可以表示为：

(4)

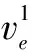
将这四点的逼近带入式(4)，得：

(5)

以点e为例，其梯度模值估计可得：

同理，可求出剩余3个半点像素的梯度模值。

将式(5)代入式(3)，得：

最后利用高斯-雅克比迭代方法进行迭代修复。目前绝大多数基于变分偏微分方程的图像修复技术都采用如上所述的步骤进行修复。修复获得的图像在边缘部分过渡不自然，容易出现模糊的情况，且准确度和精确度不够高，P-Laplace修复算法也不例外。此外，该算法由于需要提前设定p值，其灵活度较低，整个修复过程比较耗时。

2 本文修复算法数值实现

为提高修复图像的精度，充分利用待修复像素的八邻域信息，即Λ={E,N,W,S,NE,NW,SW,SE}，如图2(a)所示。为简化实现过程，将Λ分为Λ1和Λ2两部分，Λ1={E,N,W,S}，Λ2={NE,NW,SW,SE}。相应地，邻域对应的半点像素集为：α1={e,n,w,s}和α2={ne,nw,sw,se}，如图2(b)～(c)所示。

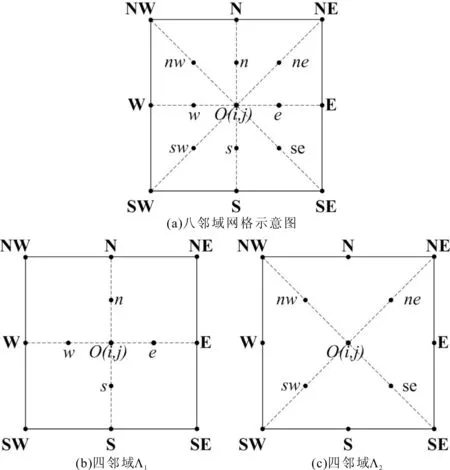
图2 分解网格示意图

在两个四邻域中，分别采用半点差分格式方法进行离散化求解，得到四邻域Λ1中的迭代式子uO1和四邻域Λ2中的迭代式子uO2，最后进行加权平均得到整体的迭代式子uO，具体实现如下。

2.1 算法自适应参数p的实现

文献[15]提出的算法由于需要事先通过大量实验找寻合适的p值，使得算法的灵活性受限。因此，本文采用自适应P-Laplace的图像修复模型，定义为：

(6)

根据梯度模值|▽u|和曲率k的关系可得：

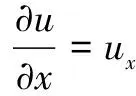
(7)

2.2 四邻域Λ1中的迭代

上述变分偏微分修复算法以及许多改进算法均是利用目标像素O(i,j)的四邻域Λ1={E,N,W,S}作为已知信息进行扩散。根据前述分析，在图2(b)中进行等间隔采样，令步长h=1，Q∈Λ1={E,N,W,S},q∈α1={e,n,w,s}，解得：

(8)

在图2(b)的四邻域Λ1中，令：

(9)

(10)

(11)

(12)

(13)

将式(9)～(13)代入式(7)，便能得到四邻域Λ1中的自适应系数p1。

2.3 四邻域Λ2中的迭代

在图2(c)中进行等间隔采样，令步长h=1，Q∈Λ2={NE,NW,SW,SE},q∈α2={ne,nw,sw,se}

V'=(v1,v2)=|▽u|p-2▽u。

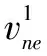
以点ne为例，其梯度模值估计可得：

同理，可求出α2剩余三个半点像素的梯度模值。

解得：

在图2(c)的四邻域Λ2中，令：

(14)

(15)

(16)

(17)

(18)

将式(14)～(18)代入式(7)，便能得到四邻域Λ2中的自适应系数p2。

2.4 八邻域Λ中的迭代

最后采用高斯-雅克比迭代方法，得出待修复点O(i,j)的像素值的迭代公式为：

(19)

3 实验结果及分析

在InterCorei3-3200 3.30GHz/4GB/Windows7 /MTALAB7.0环境中，对500×375pixels的灰度图像(动画图像和pooh图像)与512×384pixels标准测试灰度图像peppers进行处理。为了充分保证实验的客观性，实验中所有的图像像素值归一化到0～1之间，迭代次数为500次。加入文献[5]、[7]、[8]、[15]提到的算法进行分析比较，这几种算法均严格按照原参考文献中作者的要求进行参数设置，以保证实验数据的准确度。

3.1 参数设置

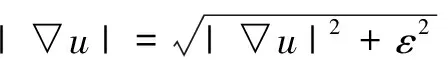
3.2 评价方法

评价方法采用主观感受结合客观方法，客观方法[17～18]利用峰值信噪比(PSNR)，噪声抑制均方误差(MSENS)和纹理结构相似度(TSSIM)进行评价，主观评价[19]采用SA主观分值评价方法。TSSIM与MSENS的定义如下：

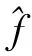
3.3 实验结果分析

图3(a)为原始清晰的动画图像，图3(b)为原始的peppers图像。图4(a)为文字受损的动画图像，图5(a)为划痕受损的peppers图像。

图3 原始图像

利用文献[5]、文献[7]、文献[8]和文献[15]及本文提出的算法分别处理图4(a)，处理结果如图4(b)～(f)所示。

图4 无噪文字受损修复结果

从图4(a)可以看出，该图受损尺度较大，掩码为黑色的文字。经过几种算法修复后，图4(d)和图4(f)的视觉效果较好，最接近原始图像。图4(e)能够看到明显的梯度效应(图中表现为黑点)，图4(b)和图4(c)在左边第二只羊的耳朵和羊角处出现了大小不一的“空缺”。同样采用上述几种算法分别处理图5(a)，结果如图5(b)～(f)所示。

图5显示，划痕受损图像经过几种算法修复后，图(d)和图(f)的修复效果最佳，比较接近原始图像。对比原始图像发现，图(b)和(c)都有不同程度的模糊，图(c)在其中一个“辣椒”还出现了小部分的空缺。图(e)的视觉效果较差，梯度效应比较明显。

图5 无噪划痕受损修复结果

3.4 实验评价

图4和图5显示，在处理无噪声的受损图像时，文献[8]提出的基于模糊C-均值的自适应TV算法和本文提出的八邻域自适应P-Laplace算法修复图像获得的视觉效果较好，另外三种利用四邻域信息的算法得到的修复图像出现了梯度效应和大小不一的“空缺”，图像过渡不自然，甚至还有模糊的现象。图6显示，采用相同的算法去除高斯噪声获得的修复图像，利用八邻域信息更能保护图像的纹理和细节。

表1、表2和表3分别列出了几种修复算法修复得到的客观评价。

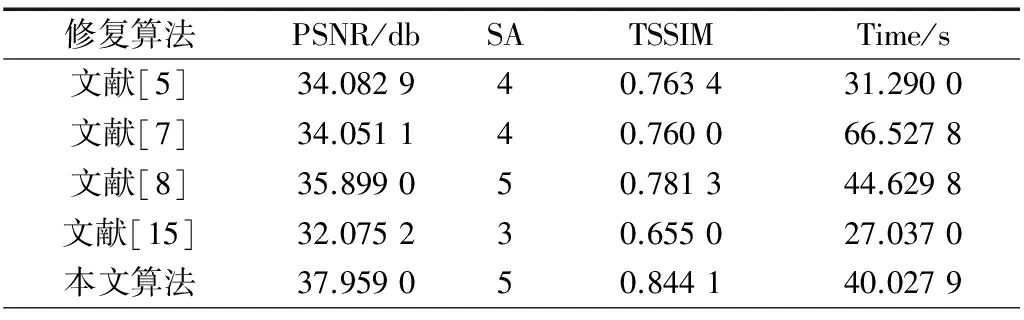
表1 不同算法修复动画受损图像的结果评价比较

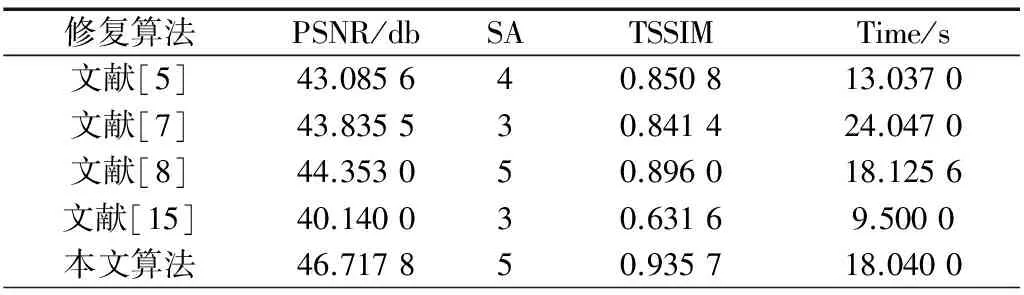
表2 不同算法修复peppers受损图像的结果评价比较

从表1和表2不难看出，本文提出的基于八邻域的自适应P-Laplace算法获的PSNR值和SA值最高，修复时间比较合理，TSSIM系数最高。需注意的是，表1、表2中的修复时间存在误差，尤其是文献[5]、文献[7]和文献[15]所提的算法。由于这3种算法都需要预先通过大量实验以获取利于图像修复的最佳修复参数，所以从整体的修复过程来看，耗费的时间绝对超出表中得到的时间。此外，相同参数对于不同的测试图像会导致不同的结果，人为操作繁琐，并且无法保证获得的修复图像是最佳的。

4 结语

本文针对变分偏微分算法只利用待修复像素点的四邻域信息进行修复的不足，充分利用八邻域信息进行修复，较好地克服了梯度效应，修复图像精度不高以及噪声抑制不充分等问题。此外，为解决因参数过多而造成的人工操作繁琐，修复结果不准确等问题，提出了自适应算法，根据受损图像自身像素变化特征自动修复，缩短了因事先通过实验确定参数所耗费的时间。实验证明此算法在主客观评价上优于传统的基于四邻域的变分偏微分修复算法。实验中的动画图像和peppers图像受损大小不同，前者受损尺度较大，修复获得的PSNR值和TSSIM值与后者相比较低，间接反映此方法更适合修复小尺寸的受损图像。下一步将考虑与基于纹理的方法有机结合以解决该问题。

[1] CHAN R,CHAN T F,YIP A,et al.Numerical methods and applications in total variation image restoration[J].Springer Reference,2015,1(1):1-28.

[2] RUDIN L,OSHER S.Nonlinear total variation based on noise removal algorithms[J].Physica D,1992,60(4):259-263.

[3] BERTALMIO M,SAPIRO G,CASELLES V,et al.Image inpainting[C].Proceeding of ACM SIGGRAPH 2000,New York,USA:ACM Press,2000:417-424.

[4] CHAN T F,SHEN J.Nontexture inpainting by curvature driven diffusions[J].Journal of Visual Communication & Image Representation,2001,12(4):436-449.

[5] 何凯,张涛,梁然.一种基于全变分模型的图像修复改进算法[J].光电子·激光,2010,21(12):1890-1893.

[6] GUARMAH E M,BOUJENA S,BELLAJ K,et al.An improved nonlinear model for image inpainting[J].Applied Mathematical Sciences,2015(9):6189-6205..

[7] 印勇,李丁,胡琳昀.采用CDD模型的自适应图像修复算法[J].重庆大学学报,2013,36(4):80-86.

[8] LIU J S,LIU H,QIAO S P,et al.An Automatic Image Inpainting Algorithm Based on FCM[J].Scientific World Journal,2014(3):983-990.

[9] 徐立军,杨秋翔,雷海卫.一种基于压缩感知的改进全变分图像去噪方法[J].微电子学与计算机,2016,33(6):100-103.

[10] 任澍,唐向宏,康佳伦.利用纹理和边缘特征的Criminisi改进算法[J].中国图象图形学报,2012,17 (9):1085-1091.

[11] 江平,张锦.一种结合CDD模型和Criminisi算法的图像修复算法[J].图学学报,2014,35(5):741-746.

[12] LI Y,JEONG D,CHOI J I,et al.Fast local image inpainting based on the Allen-Cahn model[J].Digital Signal Processing,2015,37(1):65-74.

[13] BELHACHMI Z,KALLEL M,MOAKHER M,et al.Weighted harmonic and ginzburg-landau equations in image inpainting[J].International Journal of Numerical Analysis & Modeling,2015,21(4) :12-16.

[14] 老大中.变分法基础[M].第3版.北京:国防工业出版社,2015:53-61.

[15] 李丹,仲崇权,王世强等.基于全变差和P-Laplace模型的混合图像修复算法[J].大连理工大学学报,2014,54(6):676-681.

[16] CHAN T F,SHEN J.Mathematical models for local nontexture inpaintings[J].Siam Journal on Applied Mathematics,2015,62(3):1019-1043.

[17] 赵雪青.降质图像复原方法研究[D].西安:陕西师范大学,2013.

[18] 王威,刘婧,杨蔚蔚,等.基于DCT域纹理结构相似度的模糊图像质量评价[J].计算机工程,2015,41(11):253-256.

[19] MA L,LI S,NGAN K N,et al.Reduced-reference image quality assessment in reorganized DCT domain[J].Signal Processing:Image Communication,2013,28(8):884-902.

(责任编辑：陈福时)

Adaptive P-Laplace Image Inpainting Algorithm Based on Eight Neighbors

To solve the problems of traditional variation inpainting algorithms caused by simply utilizing four neighbors,like unnatural image transition and strong manual intervention,an adaptive P-Laplace algorithm is devised based on eight neighbors.Firstly,it divides eight neighbors into two four-neighbors,and discretizes points to be repaired by central format difference in each four-neighbor.Then,determines the best p value of each four-neighbor with the adaptive method.Finally,weights and averages two four-neighbors.The simulation experiment results show that we get better PSNR and TSSIM values through the algorithm proposed in this paper,compared with other algorithms in recent years.And the PSNR values are increased by 5.74%～ 22.15%.The TSSIM values are increased by 4～30 percentage points.

Variational Image Inpainting;Neighbors;P-Laplace；Adaptive;Image Evaluation

张波(1992-)，男，四川泸州人，西华师范大学计算机学院硕士研究生，研究方向为数值计算和路由转发；徐黎明(1991-)，男，四川攀枝花人，西华师范大学计算机学院硕士研究生，研究方向为图像处理。

10.11907/rjdk.162894

TP312

A

1672-7800(2017)003-0037-05