基于小波变换和二维随机共振的图像去噪算法

刘玉欣，余 雷，刘 珊，程 伟，林 江，高仕龙

(乐山师范学院 数学与信息科学学院，四川 乐山 614000)

基于小波变换和二维随机共振的图像去噪算法

刘玉欣，余 雷，刘 珊，程 伟，林 江，高仕龙

(乐山师范学院 数学与信息科学学院，四川 乐山 614000)

小波变换能对信号特征进行自适应分类提取，并快速有效地将图像信号分解成不同频带范围内的图像分量，利于图像去噪。随机共振能将部分噪声转换成信号能量，达到增大图像对比度、提高图像质量的效果。提出了一种基于小波变换和二维随机共振的图像去噪方法，实验结果表明，该方法取得了不错的去噪效果。

小波变换；二维随机共振；图像去噪；双稳态系统

0 引言

在科学研究、军事技术、医学及天文学等领域，人们开始更多地利用图像信息来认识和判断事物，并解决实际问题。然而人们获得的图像通常会被噪声污染。为解决此问题，人们提出了许多图像去噪方法。比较常见的有各种线性滤波方法，如均值滤波、维纳滤波[1]等，还有各种变换域方法，如傅立叶变换、小波变换[2]等。1974年，法国从事石油信号处理的工程师Morlet首先提出小波变换，它是对空间(时间)和频率的局部变换，通过伸缩和平移等功能对信号进行多尺度的细化分析，从而更有效地从信号中提取信息。

噪声具有两面性。一方面，传统观点认为噪声是对信号的一种干扰，因此需要尽可能地消除或抑制它；另一方面，研究表明，噪声不是在所有情况下都起消极作用，噪声通过某些非线性系统的协同作用可以对信号起到一定增强作用。1981年，意大利学者Benzi[3]在研究古气象冰川问题时，最早提出随机共振(Stochastic Resonance)的概念。当随机噪声、输入信号和非线性系统三者达到协同时，一部分噪声将转换成信号，使原本输入的信号得到增强，进而提高输出信噪比。目前，对于随机共振在微弱周期信号的提取和参数估计方面的研究已比较成熟，但对于其在非周期信号处理，尤其是图像处理方面的应用研究还较少。因此，本文结合小波变换的频带分割特性和随机共振对噪声信号的增强功能，提出一种基于小波变换和二维随机共振的图像去噪方法。

1 小波变换图像去噪原理

小波变换是近年来应用广泛的一种数学工具，是一种多分辨率分析方法，在时频两域都具有表征信号局部特征的能力，利用它可以聚焦分析对象的任意细节。通过两个一维的高通和低通分解滤波器先后作用于数字图像的行和列，可以实现图像的二维小波分解。在每一个分解尺度上都得到4个不同的次级子带，其中LL是低频子带，它代表图像的主要内容信息，集中了图像的绝大部分能量，而LH、HL和HH是中高频部分，分别代表图像水平方向、垂直方向和对角线方向的细节。如果对图像的低频部分进一步作小波分解，则可得到多个尺度的图像时频信息。

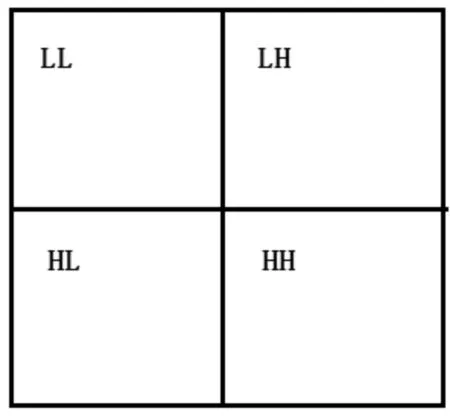
图1 小波分解

数字图像的小波分解实质上是把图像信号分解成不同频带范围内的图像分量。每一层小波分解都将图像分解成4个子带，很好地分离出表示图像内容的低频信息与表示图像细节的高频信息。因此，在不同的小波尺度上，采用不同方法来增强不同频率范围内图像的细节分量，再把处理后的系数进行小波重建，从而能够在突出图像细节特征的同时，有效抑制噪声的影响，使图像更加清晰。

2 双稳态随机共振

在随机共振的研究中，非线性双稳态模型应用较为广泛。该系统可由非线性方程来表示：

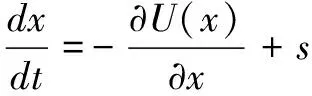
(1)

式中，U(x)是势函数，s(t)是系统的输入，分别表示为：

(2)

(3)

其中a和b为系统参数，决定势函数的形态。f(t)为周期或非周期输入信号，ξ(t)为随机噪声。从物理角度上看，双稳系统的输出模拟了粒子在势阱内的运动轨迹。

假设A为输入信号的幅值，当输入系统噪声为零时，系统存在临界值Ac。当AAc时，粒子才能在两势阱间做大范围的跃迁；当引入噪声后，在噪声的作用下，即使在A<

3 算法分析

双稳系统和小波变换均具有低通滤波器的特性。小波变换通过频域分解，可以有效地去除高频噪声成分。双稳系统利用随机共振机制能将噪声能量转化为图像信息，从而达到提高图像质量的效果。本文算法主要分为以下步骤：

(1)小波变换。将灰度噪声图像进行一层二维小波分解，得到一个低频子带LL，两个中频子带LH、HL和一个高频子带HH。图像经二维离散小波分解后,绝大部分图像信息都集中在低频部分LL，而高频噪声则集中在高频子带HH。因此,将得到的低频子带LL进行小波重构得到一个低频子图，从而达到去噪的目的。

(2)二维随机共振。根据绝热近似[4]或线性响应理论[5]，系统输入必须符合SR的小参数要求，即信号的幅度和频率以及噪声强度均远远小于1。因此，在小波重构的低频子图输入随机共振系统之前，需要先进行归一化处理，然后利用二维随机共振原理[6]，对归一化后的图像按行和列分别转化为向量输入双稳系统进行处理，以此实现对噪声的抑制和对图像的增强。

(3)直方图均衡。由于随机共振会导致图像的像素统计直方图分布在一个狭窄区域，使图像亮度增加。因此，最后利用直方图均衡，使处理后的图像像素统计分布更加均匀，从而达到增强视觉效果的作用。

4 实验效果

实验对象选取640×640的灰度图像。添加强度为D的高斯白噪声，先进行二维离散小波变换，再按上述算法对含噪图像进行随机共振。在双稳系统求解中，计算步长为h=0.1，系统参数a=4,b=80,在不同噪声强度下的实验效果如图2～图4所示。其中，(a)图是添加噪声后的图像，(b)图是小波去噪后的图像，(c)图是经小波去噪和行向量随机共振后的图像，(d)图是经小波去噪和二维随机共振后的图像。从实验效果看，本文算法能很好地达到去除噪声、增强图像清晰度的目的。既使在噪声强度达到D=0.2,噪声图像破坏程度很高的情况下，也能达到较好的复原效果。

图2 小波变换和二维随机共振去噪效果(D=0.02)

图3 小波变换和二维随机共振去噪效果(D=0.1)

图4 小波变换和二维随机共振去噪效果(D=0.2)

小波变换能将图像信息中的高、中、低频成分进行有效分离，从而达到去除噪声的目的。从实验结果看，尽管采用小波低频子带重构的复原图像与噪声图像相比，图像质量具有一定程度提高，但是小波在去除中高频成分中噪声的同时，也带走了一些图像的细节信息。利用双稳系统的随机共振机制可实现图像信号的增强功能，从而达到提高图像清晰度的目的。同时，双稳系统能将部分噪声能量转化为图像信息，从而弥补小波去噪中因舍弃中高频子带而丢失的图像细节信息。因此，从理论上而言，将小波变换和二维随机共振相结合，能达到更好的噪声图像复原效果。

假设有m行n列的灰度图像K和处理后的图像I,其峰值信噪比定义为：

(4)

其中，maxI为图像I的灰度最大值，均方差mse定义为：

(5)

图5是本文算法和小波去噪、二维随机共振去噪的效果比较。其中，(a)图是添加强度为D=0.15的高斯白噪声后的图像，(b)图是小波去噪后的图像，(c)图是经二维随机共振去噪后的图像，(d)图是本文基于小波和二维随机共振去噪后的图像。从视觉效果看，小波变换和二维随机共振均能有效地去除噪声，但是将两种方法结合后，复原效果好于单一算法。

图6是本文算法和小波去噪、二维随机共振去噪结果的峰值信噪比(PSNR)的比较。从定量角度看，只有在噪声极少的情况下，小波去噪的效果优于随机共振方法和本文算法，但当噪声强度增大，本文基于小波和随机共振的图像去噪算法取得的峰值信噪比好于单一的小波去噪和随机共振去噪。因此，本文提出的算法具有一定的实际应用价值。

5 结语

本文提出一种基于小波变换和二维随机共振的图像去噪声算法。小波变换处理噪声图像后，大部分图像信息位于低频子带，将其重构后的低频子图向量化后输入双稳系统进行二维随机共振处理。从实验结果看，能取得较好的复原效果。另外，由于随机共振后的图像像素统计直方图集中于比较狭窄的区域，因此借助于直方图均衡，能有效地增加图像对比度，从而获得更好的去噪效果。最后，由于很难界定非周期输入的双稳系统是否达到最佳的随机共振状态，因此只能通过手动调节系统参数a、b，使二维随机共振的效果达到最佳，这需要在理论上作进一步研究。

图5 去噪算法效果比较(D=0.05)

图6 去噪算法峰值信噪比比较(D=0.05)

[1] ANGELOPOULOS G, PITAS I. Multichannel wiener filters in color image restoration[J].IEEET Transactions on Circuits and Systems for Video Technology ,1994, 4(1): 83-87.

[2] 陈武凡.小波分析及其在图像处理中的应用[M].北京:科学出版社，2002.

[3] BENZI R, SUTERA A, VULPIANA A.The mechanism of stochastic resonance[J]. Phys. A, 1981, 14 (11): L453-L457.

[4] MCNAMARA B，WIESENFELD K，ROY R. Observation of stochastic resonance in a ring laser[J]. Phys. Rev Lett., 1988, 60 (25): 2626-2629.

[5] DYKMAN M I, LUCHINSKY D G, MANNELLA R, et al. Stochastic resonance: linear response theory and giant nonlinearity[J]. J Sat Phys, 1993, 70(1/2):463-479.

[6] 赵尔华，冷永刚.图像二维随机共振研究[D].天津：天津大学,2011.

(责任编辑：黄 健)

四川省教育厅资助科研项目(16TD0029)；乐山师范学院创新创业训练计划资助项目(201510649004，201610649020)

高仕龙(1975-)，男，四川仁寿人，博士，乐山师范学院数学与信息科学学院教授，研究方向为分数阶微积分、随机共振。本文通讯作者为高仕龙。

10.11907/rjdk.162550

TP312

A

1672-7800(2017)003-0034-03