直线与圆锥曲线的位置关系专题讲解

山东省聊城第一中学 崔金霞

直线与圆锥曲线的位置关系专题讲解

山东省聊城第一中学 崔金霞

一、高考目标

（1）能用坐标法解决一些与圆锥曲线有关的简单几何问题（直线与圆锥曲线的位置关系）和实际问题；

（2）进一步感受数形结合的思想、函数与方程思想、等价转化思想。

二、要点再现

1.直线与圆锥曲线的位置关系

从几何角度看，可分为三类：有两个公共点，有一个公共点及没有公共点。

从代数角度看，将表示直线的一次方程和表示圆锥曲线的二次方程联立成方程组，实际上是研究方程组解的个数问题.通过消元后得到关于x(或y)的一元二次方程，最终化归为该方程解的情况。特别提示：二次项系数为零的情况。

2.弦长问题

（1）联立方程组求两交点的坐标，然后运用两点间的距离公式求解。

（2）若直线的斜率为k,被圆锥曲线截得弦AB两端点坐标为（x1,y1）,(x2,y2),则弦长公式为或

（3）含焦点的弦长问题，要注意应用圆锥曲线的定义。

分 析： 设 椭 圆 截 直 线l于A(x1，y1)，B(x2，y2)两 点， 由消去y，得5x2＋8tx＋4(t2－1)＝0。

计算完毕后，比较竣工和设计标高差异值。其中在公式（2）中的可以直接作为实际施工立模标高。正向分析法主要是按照实际施工的步骤顺序进行桥梁施工数据的分析测算，合理解决了传统的倒装分析法不可避免的桥梁连续施工混凝土收缩不变的计算问题[3]。假设在实际计算过程中，桥梁施工单位在第一阶段应力并没有通过，也可以及时进行调整。此外，正向分析法可以充分考虑设计资料和相应施工方案，对桥梁结构工程、施工工作以及后续的工程监管融为一体，保证监管工作的现实性和针对性。

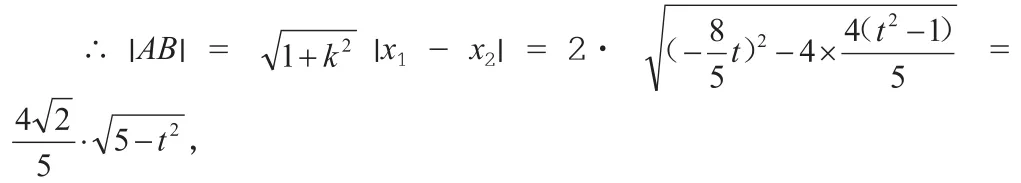
3.弦的中点问题

（1）先求弦的两端点的坐标，然后利用中点坐标公式。

（2）联立成方程组,消元后得到关于x(或y)的一元二次方程,然后利用判别式和根与系数的关系。

例3 直线y＝kx－2与抛物线y2＝8x交于A、B不同的两点，且AB的中点横坐标为2，求k的值。

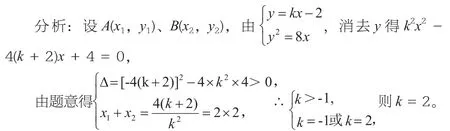
4.直线与圆锥曲线相离时,求曲线上的点到直线的最短（长）距离

主要求法有：（1）函数法，（2）数形结合法。

例4 在抛物线y2＝4x上求一点P，使得点P到直线y=x+3的距离最短。

解法一：在同一个坐标系中画出抛物线与直线的方程，发现直线与抛物线相离，最短距离就是抛物线的一条与y=x+3平行的切线到直线y=x+3的距离，从而转化成求切点即为P点坐标。

当取得最小值时y0=2，x0=1，则P点坐标为（1,2）。

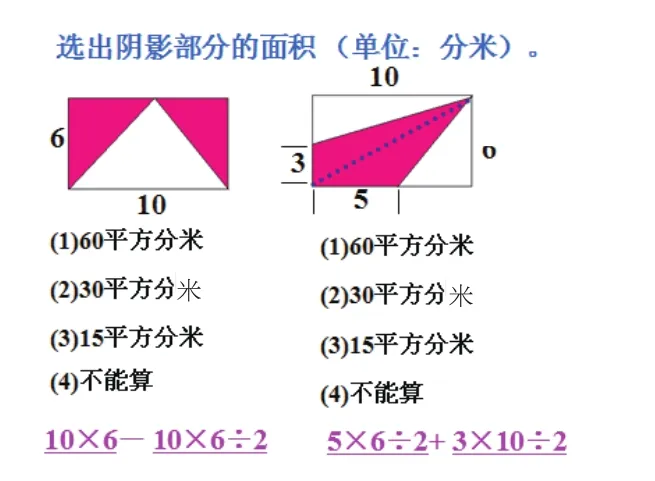
3.实践活动

请你计算一面少先队中队旗的面积，需要测量哪些数据。请找一面中队旗测量并计算。

通过组合图形的巩固练习，让学生在实践中获得分块、加减及割补的方法，并在不断的思考中将思维引向更深处，使解决问题的能力获得进一步的提高。