勾股定理的发现及证明方法杂谈

江苏省宜兴市树人中学 黄 尧

勾股定理的发现及证明方法杂谈

江苏省宜兴市树人中学 黄 尧

在科学的殿堂里，对于理论的研究是亘古不息的，不论是哲学还是自然科学，对于数学而言，更是如此，对于数学理论进行研究，不仅仅能在数学的殿堂里看见光明，更能在现实的应用中找到答案。作为一名初中数学教师，在闲暇的时间里，颇爱对于数学的一些定理进行研究，借此文章与大家共勉。

勾股定理；发现证明

发现与证明是数学研究的两个基本的主题，数学的历史发展正是由于发现与证明而光彩熠熠的。本文主要对勾股定理的发现过程及其证明过程进行简述。

一、勾股定理的发现

勾股定理是世界数学史上的第一个里程碑，但是中西方对于它的发现优先权一直存在着争议。中国对于勾股定理的发现最早能追溯到公元前一世纪的《周髀算经》，这本书里面主要涉及的数学内容是：勾股定理，测量术与分数运算。书中记载的内容是：“若求邪至日者，以日下为勾，日高为股，勾股各自乘，并而开方除之，得邪至日。”（《周髀算经》上卷二）。

国外对于勾股定理统一称之为“毕达哥拉斯定理”。传说中，为了庆祝发现毕达哥拉斯定理，毕达哥拉斯的学派曾经宰牛来庆祝。之所以被称之为“毕达哥拉斯定理”，是因为大家相信它是由古希腊的数学家“毕达哥拉斯”所发现的，或者至少是他最先证明的，但是这些说法都没有十分确切的证据来支撑，但是由于古希腊的另外一位学者阿波罗多洛斯写的一首诗中曾经提到过毕达哥拉斯证明过一个很重要的定理，此时对于是否是勾股定理尚未有明确认识，之后的阿特纳奥斯，波菲利，第欧根尼，普罗科洛斯等一些学者根据阿波罗多洛斯的话进行推断，都相信是由毕达哥拉斯所证明的，于是在公元三世纪后，“毕达哥拉斯定理”便被国外一直沿用至今。

除中国和希腊的发现之外，古埃及因为能测量直角三角形的土地，在其中有勾股数的出现，但是尚未有确切的文字证明古埃及人发现过勾股定理；古巴比伦的一些泥板中已经出现了一些很复杂的，比其他当时任何文明都复杂的勾股数，故而我们可以知道，古巴比伦人已经掌握了一般的勾股定理和勾股数的公式，这是不容置疑的。对于古印度而言，在印度古书《测绳的法规》中明确指出了勾股定理：矩形对角线给出的面积，等于长和宽分别给出的面积之和，其中还出现了很多“勾股数”，即的正整数解。

上述所涉及勾股定理的发现，我们可以更进一步来探讨。其中有的国家提出的勾股数的发现无论是多个还是单个，都只能是科学发现的开端，其实并没有完成科学假说的提出。单个特殊值处于发现的最开端，多个特殊值临近具有结构，但是与发现假说相差甚远。只有提出了勾股定理发现假说的一般形式，才能称之为发现。而中国、希腊和印度都于勾股定理做出了发现，但在时间上面，中国与希腊相仿，都是在公元前，虽然中国早50年，但是由于古代科学发现优先权在时间上以几十年为基准，所以两者的发现没有“时间上的差异”。下面笔者将根据自己对于勾股定理的一些思考，对勾股定理的证明做一些简论。

二、勾股定理的证明

数学是一门严格讲究论证的学科，它的任何结论都需要人们的逻辑推理来进行一步步的证实。未经证实的论断只能是命题，只有经过证明的才能叫作定理。对于勾股定理的证明，古今中外有很多人都证明过，直到现在为止仍有人对它进行证明。

1.经典的证明方法

（1）刘徽的证明

在公元三世纪，我国古代学者刘徽注释了《九章算术》这一数学名著，在其中的卷9《勾股》中载明“勾股各自乘，并而开方除之，既弦”，“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也，合成弦方之幂，开方除之，既弦也”。从上述的表达中可以看出刘徽是根据某种图形，借助出入相补来对勾股定理进行证明的。但是刘徽的图已经失传，后人补绘了许多种图形来推测刘徽的证明，以十九世纪清代的数学家李锐《勾股算术细草》、李潢《九章算术细草说》所采用的出入相补图最为典型。图1中，a2+b2=Ⅰ+Ⅱ+Ⅲ+Ⅳ+Ⅴ，令Ⅰ→Ⅰ’，Ⅱ→Ⅱ’，Ⅲ→Ⅲ’，Ⅳ→Ⅳ’，Ⅴ→Ⅴ’，其余部分不动，则有a2+b2=Ⅰ’+Ⅱ’+Ⅲ’+Ⅳ’+Ⅴ’，即a2+b2=c2。由此看出刘徽与赵爽是两种不同的证明方法，刘徽使用的图验法，而赵爽后面需要进一步的代数运算。

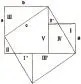
图1

（2）欧几里得的证明方法

现今存在的最早的最完整的证明是古希腊数学家欧几里得的证明。如图2，设正方形AGFB、ACKH与BDEC分别是Rt△ABC三边上的正方形，连接AE、BK，作AL与DE垂直，并且与BC相交于M，与DE相交于L，用边角边判定法可以证明△BKC≌△EAC，但是正方形ACKH的面积是△BKC的2倍，同理，长方形MLEC的面积是△EAC的2倍，故长方形MLEC的面积与正方形ACKH的面积相等。同理可证，正方形AGFB与长方形BDLM的面积相等。于是正方形BDEC的面积等于正方形ACKH与正方形AGFB的面积之和。由此欧几里得所表述的勾股定理便进行了证明。需要注意的是，这里所讲的是纯粹几何图形之间的关系，并没有涉及到数，但是其证明过程却是非常严谨的。

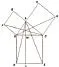
图2

（3）总统证明法

加菲尔德是1876年美国众议院的议员。他独立发现了勾股定理一个很好的证明方法。如图3，设BC、AC、AB是任一直角三角形的三边，在B点做三角形ABC的全等三角形BDE，使C、B、E在同一直线上，可得直角梯形ACED。它的面积S有两种计算方法，一种是三个直角三角形面积之和，一种是梯形面积公式。即+c2/2。由此可以推出a2+b2=c2。在5年之后，加菲尔德被选为美国第20任总统，但是仅仅任职4个月便遭枪击，在当年的9月份去世。他关于勾股定理的证明在1882年被发表，被称之为总统证法。

图3

2.证明方法的思考和总结

勾股定理有多种证明方法，在此笔者就不一一举例了。这些方法是有规律可循的，可以简单分成三类：算法化证明、演绎性证明和代数计算证明。其中算法化证明以古代中国的证明方法为代表，其所应用的“出入相补原理”是我国古代几何学最为基本的思想方法。演绎性证明以古希腊的证明方法为代表。代数计算证明是中西古代数学思想方法的结合。这些方法之中既结合了算法思想，又体现了演绎推理。比如上文所说的“总统证法”。在数学的殿堂里，勾股定理的发现与证明对于几何学的发展十分重要，作为平面几何中的一个基本定理，勾股定理对于解决三角形的问题发挥着重要的作用，同时它也是中国几何的根源，中华数学的精髓。像开方术、方程术、天元术等方法的诞生和发展，寻根溯源，都和勾股定理密不可分。在世界上，勾股定理也推动了几何学的发展。

在新课标以及教材的更新背景下，教育事业慢慢开始重视数学知识的发生和发展过程，其主要目的是为了促进学生的自主探索。作为数学教师，我们的能力或许不足以支撑我们像古往今来的数学专家那样发现、证明数学中的定理、公式，但我们却可以通过自己对新知的不断探索以及对数学理论最新研究成果的关注，不断革新自身的相关理论知识，从而为自己的教学增添丰富的知识储备。中考数学试卷中，勾股定理的命题题型多样，分数占比可观，勾股定理在初中数学学习中的重要性可想而知。为更好地使学生对勾股定理产生深刻的理解，也为了让学生能够切实掌握勾股定理这一数学知识，使他们在中考试题中能够充分运用这一定理进行解题，教师可以对学生进行简单证明方式的讲解，引起学生对于勾股定理的关注，教师将自身的知识经验逐渐传授给学生，帮助他们更好地进行数学学习。

[1]陈洪鹏.勾股定理研究[D].辽宁师范大学，2011.

[2]王锋.重现数学家验证勾股定理的探究之路[J].中学生语数外：初中版，2011.

[3]张程.数学活动课《关于勾股定理的研究》教学案例[J].数学学习与研究，2010.