关于导数解法
2017-04-10王祥厅
数学大世界 2017年9期
关于导数解法
四川省宜宾市龙文实验学校 王祥厅
一、设而不求

二、导数中的主次变换
用常量表示变量,用变量表示常量。

三、转化思想
2个变量转化为一个(x1,x2),则:
①将x1看作常数,x2作为变量;
②用x2表示x1,最终化为关于x2的函数;
例3 已知函数f(x)=ln(1+x)-x,g(x)=xlnx,0<a<b,求证:

即原不等式成立。
设x1<x2,则有x1<1<x2。
要证x1+x2<2,即证x1<2-x2,
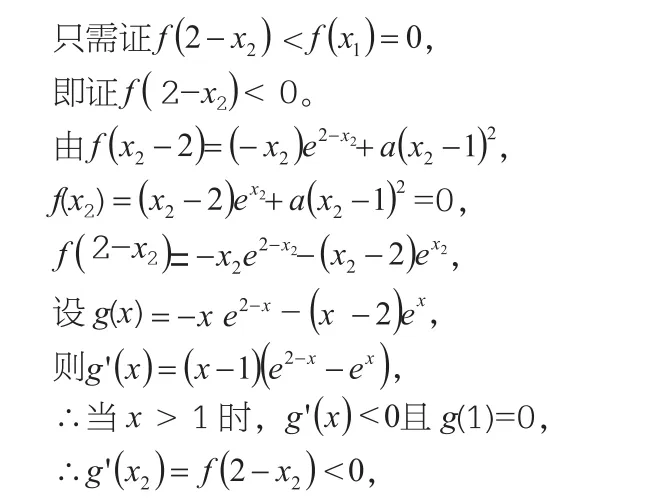
即x1+x2<2成立。

四、先必要再充分
求字母参数的取值范围时,可先求出其必要条件,将需要讨论的范围压缩,再进一步求出充分条件。

五、洛必达法则
在求f(x0)的值时,x0在定义域之外或代入x0却使得f(x0)的分母为零,无意义,这时可以使用洛必达法则计算。
