斜楔块条件下超声换能器的声场仿真

董 明， 马宏伟，陈 渊， 张旭辉， 曹现刚

(1.西安科技大学 机械工程学院，西安 710054；2.长安大学 高速公路施工机械陕西省重点实验室，西安 710054；3.西安科技大学 理学院，西安 710054)

斜楔块条件下超声换能器的声场仿真

董 明1,2， 马宏伟1，陈 渊3， 张旭辉1， 曹现刚1

(1.西安科技大学 机械工程学院，西安 710054；2.长安大学 高速公路施工机械陕西省重点实验室，西安 710054；3.西安科技大学 理学院，西安 710054)

各种大型轴类零件形状复杂，体积和质量大，拆卸困难，主要用小角度纵波探头在轴端面实施探伤。小角度纵波超声检测方法在工业中有着大量的应用，对于小角度纵波探头的声场研究还较少。以空间脉冲响应为理论基础，根据界面条件下的波形转换以及超声波的透射规律，建立了小角度纵波超声探头在斜楔块条件下的空间声压模型，给出了其空间脉冲响应的计算公式，并仿真得到了不同斜楔块角度时介质中的声压分布图，利用半圆阶梯试块测试了声轴线的声压和指向性图，实验结果和仿真计算基本一致。该方法可用于不同参数的超声探头倾斜入射时的声场仿真，为制定轴类零件非拆卸情况下的检测策略，提高检测可靠性奠定基础。

空间脉冲响应；斜楔块；小角度纵波；超声检测

大型轴类零件长期在重载条件下运行，容易产生疲劳裂纹，直接影响到重大装备的安全运行[1]。各种大型轴类零件形状复杂，体积和质量大，拆卸困难，主要用小角度纵波探头在轴的端面实施探伤[2]，小角度纵波超声检测方法在工业中有着大量的应用[3-7]，但对于小角度纵波探头的声场仿真研究还相对较少。在现代无损检测领域，提高检测的可靠性一直是热点问题[8]，在对零件进行超声检测之前，都要制作试块确定探头类型、频率、角度及适用范围，费时耗力。因此，研究斜楔块条件下超声波在工件内部的传播规律和声压分布规律，以辅助制定关键轴类零件非拆卸情况下的检测策略，对节约人力物力，特别是保证重大装备关键轴类零件超声检测的可靠性和准确性有重要意义。

小角度纵波探头的晶片安装在有一定角度的斜楔块上，晶片发射的纵波倾斜入射到界面上，从而在工件中形成折射纵波，其本质是超声波在非平行界面传播的问题。对于界面条件下的声场，很多学者都进行了研究，严仁博研究了楔形换能器在各向同性介质中纵波和横波指向性图[9]，卢超采用边界元对脉冲波激励下的临界折射纵波的传播特性和声束指向特性进行数值分析和实验测量[10]。SONG等[11]将固固界面简化为液固界面，研究了带有斜楔块的一维超声相控阵探头在不同偏转角度和聚焦深度时的声场特性，孙芳等[12]基于该方法和射线声学理论，推导了聚焦法则，得到了超声线型阵在液固界面的声场和位移场表达式，仿真了斜楔块条件下一维相控阵换能器的辐射声场，并讨论了聚焦对换能器轴向和横向声场的影响，卢超等[13]结合三维空间超声场的界面折射定律和空间几何关系，推导了二维面阵相控阵的聚焦法则，并详细分析了不同偏转角和不同聚焦深度时检测材料中的声场特性。张碧星等[14]利用射线近似方法，得到了凹面一维相控阵聚焦声场在液固界面上反射和折射后的声场渐近解析表达式，对液固界面上的反射和折射声场进行了分析和讨论。计算效率严重决定了声场仿真模型的工程应用，而空间脉冲响应是一种高效准确的暂态声场计算方法[15]，其主要还是应用于单一介质的声场计算，其在界面条件下的声场计算研究还较少，因此，研究基于空间脉冲响应斜楔块条件下的声场模型，可以扩展空间脉冲响应的适用范围，提供一种快速准确的界面条件下声场仿真方法。

本文主要研究斜楔块界面条件下的暂态声场，首先分析了斜楔块条件下不同区域声场的组成，然后根据界面条件下声透射和声反射规律，得到空间点的空间脉冲响应的计算公式，最后仿真了不同斜楔块角度时的声场分布，并进行了实验验证。

1 理论模型

1.1 半无限空间的空间脉冲响应

换能器嵌于无限大刚性板中，刚板表面振幅为零，并且假设声源上各质点振动幅值和相位相同，声波在各向同性、无衰减的介质中传播。在小振幅声波的假设条件下，声波在介质中的传播规律可以看作是线性的，超声探头发射的声场可以看作激励脉冲与空间脉冲响应函数的时域卷积。空间脉冲响应计算模型如图1所示，空间任意点P(x,y,z)处声压为

(1)

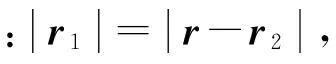
(2)

h(r,t)即换能器在空间点r处的脉冲响应函数。将求得换能器的空间脉冲响应h(r,t)代入式(1)就可以得到换能器的声场。对于不同形状的换能器，h(r,t)有成熟的求解过程，本文不再介绍。而要得到斜楔块条件下换能器的声场，就是计算斜楔块条件下的空间脉冲响应。

图1 空间脉冲响应声场计算模型Fig.1 Geometry and coordinate system used forthe spatial impulse response of a piston transducer

1.2 斜楔块条件下的空间脉冲响应

斜楔块使晶片和被检工件表面形成一个严格的夹角，以保证晶片发射的超声波按照入射角倾斜入射到分界面，从而在界面处产生波形转换，在工件内得到特定形式和角度的声束。根据Snell定理，对于给定的材料，斜楔块的角度决定着转换声波的类型与折射角度。如图2所示，换能器所在楔块平面与界面的夹角为α，晶片发射的超声纵波以入射角α倾斜入射到界面上，对于小角度纵波探头，其入射角α很小，一般小于第一临界角，在界面处发生波形转换，产生折射纵波和折射横波，纵波折射角为βl，横波折射角为βs，而且在固体介质中，纵波声速大于横波声速，所以有βl>βs。在超声波倾斜入射的情况下，工件中的声场由折射横波声场和折射纵波声场两部分组成。

图2 斜楔块条件下的波形转换示意图Fig.2 Mode conversion at the interface

设P(x,y,z)为空间任意一点，当点P位于直达纵波所覆盖的范围内时，即由上端转换的纵波T1L和下端转换横波T2S所确定的区域，如图3所示，P点声压由转换的纵波和横波共同决定，A点处发出的超声纵波在Tl处波形转换，转换纵波传播到P点，B点处发出的超声纵波在Ts处波形转换，转换横波传播到P点，在各点处的波形转换都满足Snell定理。纵波在P点的脉冲响应是：

(3)

式中，cl1是斜楔中的纵波声速，cl2是工件中的纵波声速，ηl是波形转换时纵波对应的折射系数，r1、tl分别表示入射纵波和折射纵波的声程。

同理，横波在P点的脉冲响应是：

(4)

式中，cs2是工件中的横波声速，ηs是波形转换时横波对应的折射系数，r2、ts分别表示入射纵波和折射横波的声程。

P点的脉冲响应为：

h(x,y,z,t)=hs(x,y,z,t)+hl(x,y,z,t)

(5)

图3 斜楔块条件下直达波区域声场计算模型Fig.3 Calculation of direct wave field with wedge

当P点位于直达纵波所直接覆盖的范围以外时，如图4所示，此时P点声压主要来自于边缘波的贡献，即边缘纵波ETs转换的横波TsP和由边缘纵波转换ETl的横波TlP，关于入射点Ts和Tl，可由snell定理确定。

转换纵波在P点的脉冲响应是：

(6)

转换横波在P点的脉冲响应是：

(7)

P点的脉冲响应为：

he(x,y,z,t)=hse(x,y,z,t)+hle(x,y,z,t)

(8)

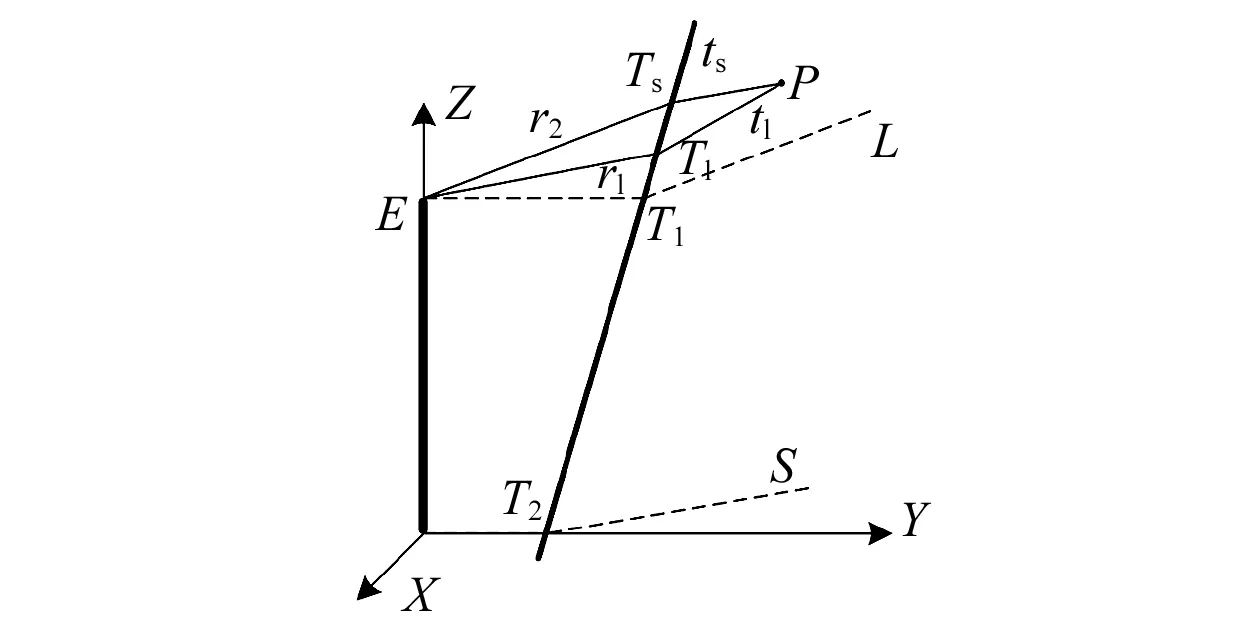
图4 斜楔块条件下边缘波区域声场计算模型Fig.4 Calculation of edge wave field with wedge

1.3 声波在边界上的反射系数和折射系数

超声波传播过程中，当遇到两种声介质的分界面时，因为声阻抗的差异，会产生声波的反射、折射和透射。因此，在界面处的反射和透射系数计算，以及波形转换后的能量分配规律就是超声计算的重点。在界面处的声学边界条件主要是：①分界面处的声压连续；②分界面处法向速度相等。声波斜入射时，一部分声波在界面反射回原介质，另一部分声波则偏离原来的入射方向透过界面，形成折射波，可以得到反射波声压与入射波声压比rp，折射波声压与入射波声压比tp分别为：

(9)

2 斜楔块条件下的声场仿真

对矩形换能器制成的小角度纵波探头空间声压进行仿真研究，晶片尺寸10 mm×8 mm，频率2.5 MHz，换能器中点距离界面10 mm。斜楔块为有机玻璃，密度1.2×103kg/m3，纵波声速2 730 m/s，钢的密度7.8×103kg/m3，纵波声速为5 900 m/s，钢中横波声速为3 200 m/s。用式(5)和(8)可以计算空间各点的空间脉冲响应，然后用式(1)得到空间点的声压，最后将声压进行归一化处理，就可以得到声场分布图。图5是斜楔块角度5°的声场，仿真使用THINKPAD笔记本电脑，CPU是Intel I5-3230，内存4 GB，编程环境为Windows 7系统下的Matlab 8.2.0.701，计算区域为30 mm×80 mm，空间步长为0.2 mm，总耗时3.833 s。

图5 斜楔块倾角为时的声场Fig.5 Simulated acoustic field with wedge of 5°

图6(a)是斜楔块角度分别为3°、4°和5°时声轴线上声压分布曲线，可见声轴线上声压分布规律基本相似，都随着距离的增大而逐渐衰减，近场区衰减较快，远场区衰减较慢。随着斜楔块角度的增大，声轴线上的声压幅值变小，这是因为当超声波入射角小于第一临界角时，折射系数随着入射角度的增大而减小。

图6(b)和图6(c)分别是斜楔块角度分别为3°、4°和5°时，在半径为30 mm和15 mm时的声场指向性曲线，可见近场区能量集中，声束较窄，随着斜楔块角度的增大，声束的偏转角度也在增大，通过改变斜楔块的角度可以得到不同偏转角度的声束。

(a) 小角度纵波探头声轴线声压曲线

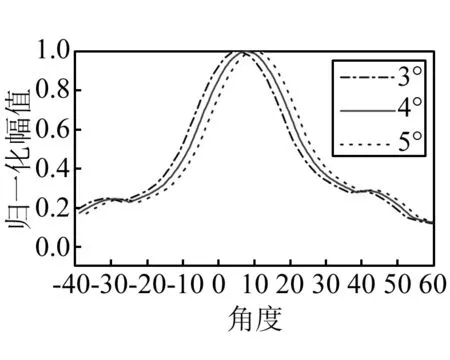
(b) 在半径30 mm圆弧上的指向性曲线

(c) 在半径15 mm圆弧上的指向性曲线

3 实 验

在固体内难以植入传感器进行声场测试，固体内声传播规律的验证是超声界一大难题，本文依据GB/T 18852—2002——《无损检测超声检验 测量接触探头声束特性的参考试块和方法》，利用HS半圆阶梯试块、数字超声探伤仪和示波器测试小角度纵波探头在固体内声场分布特征。实验系统如图7所示，发射探头晶片尺寸为10 mm×8 mm，频率2.5 MHz，为保证接触良好，将超声探头置于磁力探头座中。调节探头位置，使探头入射点置于试块上最小半径弧面圆心处，将回波调整到满屏高度的80%，并记录增益值，然后依次将探头移动到其他弧面圆心处，记录各弧面的增益值，得到声轴线上的声压曲线，最后进行归一化处理。

图7 声场测试实验系统Fig.7 Measurement set-up

图8给出了斜楔块角度为5°时仿真和实验测量得到的轴线声压曲线，两者吻合较好。图9是斜楔块倾角为5°，半径40 mm圆弧的指向性图，由图可见，仿真和实验结果吻合较好，此时折射纵波角度为10 °，与由Snell定理一致。

图8 声轴线声压Fig.8 Measurement acoustic field on axis

图9 小角度纵波探头的指向性图(α=5°)Fig.9 Measurement acoustic field off axisat 40mm with wedge of 5°

4 结 论

以空间脉冲响应为理论基础，根据波形转换规律和声学边界条件，建立了斜楔块条件下超声换能器的空间声压模型，扩展了空间脉冲响应的应用范围。

利用半圆阶梯试块测试了声轴线的声压，用小直径超声探头测试了探头的指向性图，实验结果和仿真计算一致。

该方法可以仿真不同形状、频率、角度超声换能器在斜楔块条件下的声场，为制定检测策略，提高检测可靠性奠定基础。

[ 1 ] 信瑞山, 马庆贤, 单忠德. 内裂纹高温修复组织演化过程分析[J]. 清华大学学报(自然科学版), 2015(3): 304-309. XIN Ruishan, MA Qingxian, SHAN Zhongde. Microstructure evolution of internal crack healing in a low-carbon steel at elevated temperatures[J]. Journal of Tsinghua University (Science and Technology), 2015(3): 304-309.

[ 2 ] 李智明, 寇东英. 小角度纵波探头检测轴类零件表面横向缺陷的可行性[J]. 无损检测, 2008(6): 363-366. LI ZhiMing, KOU Dongying. The feasibility research on detecting surface horizontal cracks on axis by using small-angle longitudinal wave probe[J]. Nondestructive Testing, 2008(6): 363-366.

[ 3 ] 杨平华, 梁菁, 王铮, 等. 航空发动机盘件径轴向裂纹底波监控超声检测方法研究[J]. 航空材料学报, 2014, 34(5): 88-92. YANG Pinghua, LIANG Jing, WANG Zheng, et al. Research on ultrasonic back-wall echo monitoring method for radial-axial crack of aircraft engine disk[J]. Journal of Aeronautical Materials, 2014, 34(5): 88-92.

[ 4 ] AHMED S R, SAKA M. A new ultrasonic angle-beam technique for sensitive evaluation of closed cracks[J]. NDT & E International, 2000, 33(4): 261-271.

[ 5 ] 李晓红, 王敏, 吴敏, 等. 支柱瓷绝缘子的超声检测有效性[J]. 中国电机工程学报, 2006, 26(9): 159-163. LI Xiaohong, WANG Min, WU Min, et al. Ultrasonic testing validity of porcelain post insulators[J]. Proceedings of the CSEE, 2006, 26(9): 159-163.

[ 6 ] 莫润阳. 超声小角度纵波灵敏检测疲劳小裂纹[J]. 西北大学学报(自然科学版), 2004, 34(1): 39-43. MO Runyang. A small angle incidence longitudinal wave for sensitive evaluation of fatigue cracks [J]. Journal of Northwest University (Natural Science Edition), 2004, 34(1): 39-43.

[ 7 ] UCHIMOTO T, TAKAGI T, ICHIHARA T, et al. Evaluation of fatigue cracks by an angle beam EMAT-ET dual probe[J]. NDT & E International, 2015, 72: 10-16.

[ 8 ] 胡宏伟, 彭凌兴, 李雄兵, 等. 多层构件水浸超声自动检测中的水声距优化方法[J]. 仪器仪表学报, 2014, 35(5): 1149-1154. HU Hongwei, PENG Lingxing, LI Xiongbing, et al. Water path length optimization method in automatic immersion ultrasonic testing for multilayer components[J]. Chinese Journal of Scientific Instrument, 2014, 35(5): 1149-1154.

[ 9 ] 严仁博. 超声楔形换能器的体波和瑞利表面波指向性图案[J]. 物理学报, 1974, 23(6): 419-428. YAN Renbo. Directivity patterns of angle probes for ultrasonic bulk waves and surface waves[J]. Acta Physica Sinica, 1974, 23(6): 419-428.

[10] 卢超，黎连修，涂占宽．临界折射纵波探头声束特性的边界元分析与测量[J]．仪器仪表学报，2008，29(12)：2570-2575． LU Chao, LI Lianxiu,TU Zhankuan. Boundary element analysis and measurement for beam profiles of critically refracted longitudinal wave probes[J]．Chinese Journal of Scientific Instrument, 2008，29(12)：2570-2575.

[11] SONG S J, KIM C H. Simulation of 3D radiation beam patterns propagated through a planar interface from ultrasonic phased array transducers[J]. Ultrasonics, 2002, 40(1): 519-524.

[12] 孙芳, 曾周末, 王晓媛, 等. 界面条件下线型超声相控阵声场特性研究[J]. 物理学报, 2011, 60(9): 435-440. SUN Fang, ZENG Zhoumo, WANG Xiaoyuan. et al. Acoustic field characteristics of ultrasonic linear phased array for an interface condition [J]. Acta Physica Sinica, 2011, 60(9): 435-440.

[13] 卢超, 劳巾洁, 戴翔. 带楔块二维面阵列超声相控阵声场特性分析[J]. 声学学报, 2014, 39(6): 714-722. LU Chao, LAO Jinjie, DAI Xiang. Radiation beam field characteristics of 2D ultrasonic phased matrix array transducer mounted on solid wedge[J]. Acta Acustica, 2014, 39(6): 714-722.

[14] 张碧星, 王文龙. 凹面相控阵聚焦声场在液固界面上的反射和折射[J]. 物理学报, 2008, 57(6): 3613-3619. ZHANG Bixing, WANG Wenlong. Reflection and refraction on the fluid-solid interface of acoustic field excited by a concave phased array[J]. Acta Physica Sinica, 2008, 57(6): 3613-3619.

[15] GAO H, HERGUM T, TORP H, et al. Comparison of the performance of different tools for fast simulation of ultrasound data[J]. Ultrasonics, 2012,52(5): 573-577.

Simulation of ultrasonic fields radiated by transducer through a wedge

DONG Ming1,2， MA Hongwei1， CHEN Yuan3， ZHANG Xuhui1， CAO Xiangang1

(1. School of Mechanical Engineering, Xi’an University of Science and Technology, Xi’an 710054, China;2.Key Laboratory of Expressway Construction Machinery of Shaanxi Province, Chang’an University, Xi’an 710054, China;3.School of Science, Xi’an University of Science and Technology, Xi’an 710054, China)

Owing to that a large shaft is very difficult to be disassembled because of its complicated shape, large volume and quality, the fatigue cracks of shaft components are mainly tested by using a small angle longitudinal ultrasonic wave probe arranged on the end face of the shaft.Small angle longitudinal transducers are widely used in industry and for their reliable application, it is essential to have thorough understanding about the characteristics of radiation beam patterns produced in the medium. Considering the mode conversion and refraction at the interface, a model was developed based on the theory of spatial impulse response, which can be used to calculate the ultrasonic field of the small angle longitudinal transducer under wedge conditions. The ultrasonic field distribution patterns at various wedge angles were obtained by simulation. The field distribution in a half-round stair (HS) block was measured as an example, and the measurement results are in good agreement with the simulation results. The method can be used to simulate the acoustic field of small angle longitudinal transducers with different parameters, which is helpful to make the strategy decision for shaft inspection and improve the reliability of ultrasonic testing.

spatial impulse response; wedge; small angle longitudinal wave; ultrasonic testing

国家自然科学基金资助项目(51074121)；中国博士后科学基金资助项目(2015M572653XB)；陕西省教育厅专项科学研究计划项目(15JK1455)：长安大学高速公路施工机械陕西省重点实验室开放基金资助项目(310825161124)

2016-06-22 修改稿收到日期： 2016-07-14

董明 男，博士，讲师，1984年8月生 E-mail:jesunatg@hotmail.com

TB551

A

10.13465/j.cnki.jvs.2017.06.023