基于非线性数学方法的PM2.5中重金属浓度模拟
2017-04-11冷湘梓王勤耕李慧明南京大学环境学院污染控制与资源化研究国家重点实验室江苏南京20023南京信息工程大学江苏省大气环境与装备技术协同创新中心江苏南京20044
冷湘梓,王勤耕,2,钱 新,2*,李慧明*,陆 昊(.南京大学环境学院,污染控制与资源化研究国家重点实验室,江苏 南京 20023;2.南京信息工程大学江苏省大气环境与装备技术协同创新中心,江苏 南京 20044)
基于非线性数学方法的PM2.5中重金属浓度模拟
冷湘梓1,王勤耕1,2,钱 新1,2*,李慧明1*,陆 昊1(1.南京大学环境学院,污染控制与资源化研究国家重点实验室,江苏 南京 210023;2.南京信息工程大学江苏省大气环境与装备技术协同创新中心,江苏 南京 210044)
2013年在南京市南京大学鼓楼校区和仙林校区采集PM2.5,并测试其中重金属浓度,分析重金属在不同季节和地区的污染特征及其与气象因子、常规大气污染物的相关关系.数据经主成分分析预处理后,使用 BP神经网络(BP-ANN)和支持向量机(SVM)两种非线性数学方法构建PM2.5中重金属快速评估模型,并与多元线性回归模型(MLR)进行比较.结果显示:南京PM2.5及其中重金属平均浓度冬季最高,其次为春季,夏季和秋季浓度较低.PM2.5中重金属浓度与气象因子和大气污染物间具有一定相关性.BP-ANN对大部分金属(除了Ba、Cr和V)训练模型的相关系数最高;而SVM对所有金属验证模型的相关系数最高.3种方法对Cd、Cu、Pb、Ni和Zn的模拟效果较好,对Cr、Fe、Sr、Ti和V的模拟效果相对较差.
PM2.5;重金属;BP神经网络;支持向量机;多元线性回归
PM2.5易于富集各种污染物,尤其是重金属.研究表明,PM2.5中重金属与人类呼吸系统疾病和心血管疾病的发生具有重要联系,并可能造成人体生殖发育等各种机能障碍[1-3].目前由于大气颗粒物重金属还不能满足实时监测、预报的需求,因此,建立大气颗粒物中重金属快速评估模型,对我国城市大气重金属污染防控具有重要意义.
人工神经网络(ANN)是一种模仿生物神经网络的数学模型,具有自学习功能、联想存储功能、高速收敛的优点,其中以 BP-ANN应用最为广泛,它通过反向传播误差不断调节权值和阈值,可逼近任何输入和输出间的光滑可测函数,并得到最优解[4].支持向量机(SVM)是通过寻找最大间隔超平面,引入核函数解决将低维向量空间映射到高维向量空间所带来的维数危机问题,从而进行回归分析[5].近年来这 2种非线性数学方法在模拟、预测大气环境中SO2、CO、NO2、O3、PM10和PM2.5等方面均得到了广泛研究和应用[6-13].而目前运用相关技术对大气颗粒物中重金属进行模拟和评估的研究尚未见报道.
本文以南京为研究对象,分析不同季节和地区 PM2.5中重金属污染特征,探讨重金属浓度与气象因子、常规大气污染物的相关性,使用神经网络、支持向量机和多元线性回归方法分别构建PM2.5中不同重金属的浓度模拟模型,为大气重金属污染评估提供一种新的思路.
1 实验与方法
1.1 研究区域概况
南京城区三面环山,不利于污染物的扩散,因此,城北、江北、六合、浦口等地的工业区对城区空气质量存在较大影响.本研究以南京大学鼓楼校区(118°46′E,32°03′N)和仙林校区(118°57′E, 32°07′ N)为研究区域进行颗粒物采样,2个校区分别位于市中心和城北郊区.
1.2 样品采集
使用 TE-6070型大流量颗粒物采样器(流量1.13m3/min)和 PM2.5粒径切割器采集 PM2.5,采样介质为高纯石英滤膜.采样器分别设在南京大学鼓楼校区学生宿舍楼顶和仙林校区环境学院楼顶,采样器大气入口高度距楼顶地面1.5m左右.在2013年按季节在两采样点同步采样,在无雨、无大风天气下,每个季节采集8~11d (春季:4-24~5-5;夏季:8-11~8-28;秋季:10-10~10-18;冬季:12-02~12-10),每天分别采集白天(8:00~18:00)和夜间(19:00~7:00)两个样品,共获得140个样品.
采样期间气象数据和污染物数据从南京大学鼓楼校区和仙林校区环境空气自动监测站及南京市环境监测中心站获取.
1.3 重金属提取与分析
采样前后石英滤膜恒温恒湿(温度 20~25℃,湿度40%~50%)至少24h后称重,以确定PM2.5的质量.取滤膜的1/8用于重金属浓度测定.首先,用陶瓷剪刀将滤膜剪成条状碎片,再使用 HNO3-HCl-HF-HClO4在 85~95℃下消解.使用电感耦合等离子体发射光谱仪(ICP-OES, Perkin Elmer SCIEX, Optima5300)和电感耦合等离子体质谱(ICP-MS, Perkin Elmer SCIEX,Elan9000)测定金属浓度.每批次实验过程中空白样品和质控样品进行同步测定,所有元素回收率为95%~105%.元素分析在南京大学现代分析中心进行.
1.4 PM2.5中重金属模拟模型的建立
1.4.1 数据预处理 由于输入因子较多且共线性较强时,会降低模型训练效率并影响模拟精度,而主成分分析(PCA)可对输入因子降维,消除样本间相关性,加快模型收敛速度[14].因此,本文在建模前,先将气象因子及大气污染物因子进行主成分分析,选取累计贡献度超过 90%的主成分作为新的输入因子.同时,为降低模型误差,对各主成分进行归一化处理.
1.4.2 多元线性回归模型的构建 借助 SPSS 23.0工具,采用多重线性回归(MLR)逐步回归法将气象因子和大气污染物因子作为自变量逐个引入模型,确保每次引入新的变量之前回归方程中只包含显著性变量,最后拟合得到最优的大气重金属模拟模型.模型模拟时,随机选取70%作为训练数据,剩下30%作为验证数据.为确保训练数据的代表性,随机选取区域、季节、白天和夜晚的数据,且包含其中的极大和极小值.
1.4.3 基于 BP神经网络的模型构建 借助matlab R2013a工具,使用最速梯度下降法训练BP-ANN.模型为双隐层,分别设有6和1个神经元,传递函数分别设tansig和purelin.模型训练时数据的选取原则与多元线性回归模型相同.在100次成功建模之中,选择训练模型相关系数最大的一次作为模拟模型,对重金属浓度进行模拟.BP-ANN的工作原理可参考相关书籍[15].
1.4.4 基于支持向量机的模型构建 借助matlab R2013a和libsvm-3.21工具箱,选取径向核函数(RBF核函数),epsilon-SVR 模型构建模拟模型.模型中损失函数 p值取 0.00001,交叉验证折数 v取 3,通过寻找最佳模型对应的惩罚系数c、核参数g来构建模拟模型.模型训练时数据的选取及最优秀模型选择的原则与BP-ANN相同.SVM的工作原理可参考相关书籍[16].
2 结果与讨论
2.1 PM2.5的浓度分布
如图1所示,总体上仙林和鼓楼两采样点白天和夜晚之间的PM2.5浓度无明显差异(P>0.05),春秋两季仙林浓度显著高于鼓楼(P<0.05),而秋冬两季两采样点差异性不明显(P>0.05).冬季PM2.5平均浓度最高,其次为春季,夏季和秋季平均浓度最低,该观测结果与南京的其他报道相一致[17-18].冬季由于大气低空易出现逆温层,阻碍污染物扩散,往往会造成 PM2.5浓度上升,而夏季PM2.5的低浓度可能与南京夏季东南季风及降水冲刷作用影响有关.冬季和春季绝大部分样品的PM2.5浓度超过国家标准日均限值75µg/ m3(GB 3095-2012)[19],夏季和秋季只有部分样品浓度超标.2013年12月初,南京发生严重雾霾天气,而本研究结果显示,雾霾期间,PM2.5最高浓度比国家标准高出近7倍,雾霾天气下大气颗粒物污染不容忽视.
2.2 PM2.5中重金属浓度分布
如表1所示,不同金属浓度的平均值大小为: Fe>Al>Zn>Pb>Mn>Ti>Cu>Cr>Ba>Ni>As>Sr>V>Cd>Co, Zn、Pb和Cu浓度较高,V、Cd和Co浓度较低,这与南京的其他研究报道一致[20].与PM2.5浓度分布情况类似,大部分金属夏季浓度最低,所有金属冬季浓度最高;与秋季相比,大部分金属元素春季浓度也较高.

表1 PM2.5中金属浓度(ng/m3)Table 1 Concentrations of metal elements in PM2.5(ng/m3)
对于不同采样点,春季所有金属在仙林的平均浓度均高于鼓楼,秋季所有元素在鼓楼的平均浓度均高于仙林,夏季大部分金属元素在仙林的平均浓度高于鼓楼(除了Co、Cr、Cu和Zn),冬季大部分金属在鼓楼的平均浓度高于仙林(除了Cd、Sr和V).仙林较高的金属浓度受城北以及江北主要化工园区污染排放的影响较大.而鼓楼地区较高的金属浓度与密集的交通污染、居民日常活动以及郊区大气污染物在市中心的汇集有关.
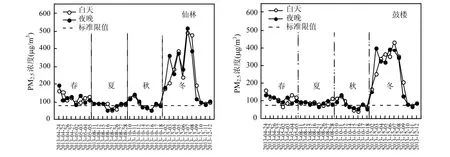
图1 PM2.5浓度的时间趋势Fig.1 Temporal trends of PM2.5concentrations
受地理位置、气象条件及人为源释放的影响,与其他研究相比(表 2),PM2.5中重金属浓度在不同城市差异较大.重庆 PM2.5中大部分重金属(As、Cd、Cr、Mn和Zn)浓度较高,其次是济南、成都和广州,而南京大气重金属污染整体上处于中等水平.
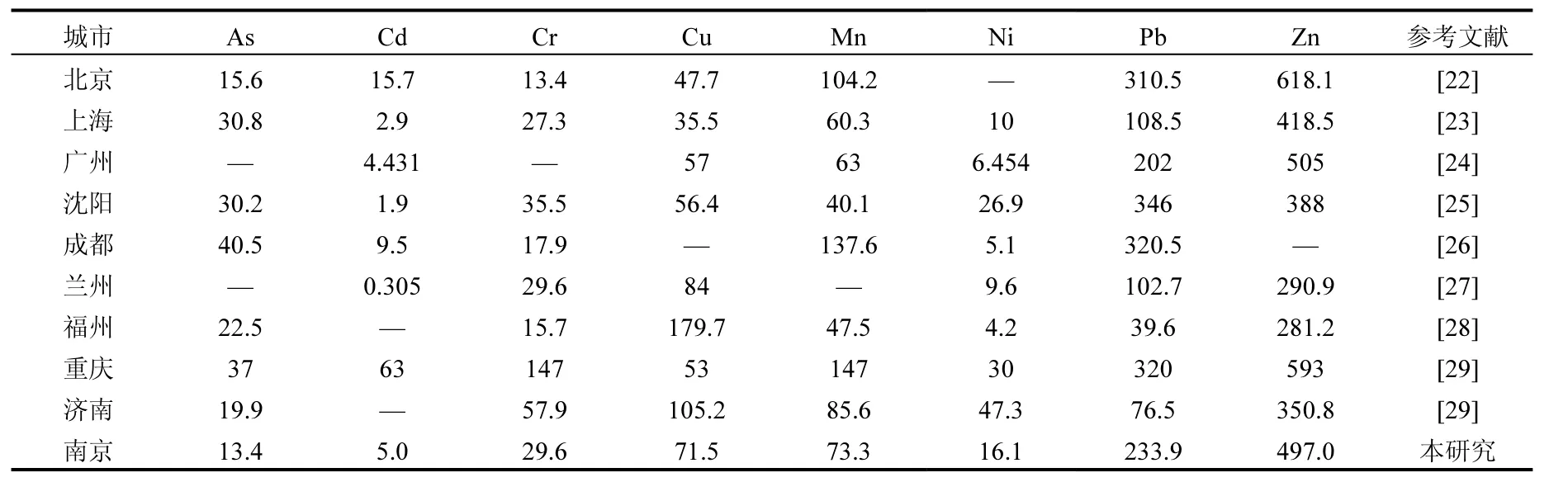
表2 南京PM2.5中重金属浓度与部分城市的比较(ng/m3)Table 2 Comparisons of heavy metal concentrations in PM2.5in Nanjing with other cities(ng/m3)
2.3 PM2.5中重金属与预测因子的相关性
为验证模型输入参数与金属的内在关联,对金属浓度与气象因子和大气污染物的皮尔逊相关系数进行分析.如表3所示,大部分金属与湿度无显著相关性,由于采样尽量选取晴朗无雨天气,因此湿度对大气重金属的影响不太明显.金属浓度与风速、温度呈显著负相关,与气压呈显著正相关.风速对大气污染物有一定稀释作用,风速越高越容易降低大气颗粒物浓度.一般来说,温度越高,大气压越低,空气对流运动越明显,大气颗粒物扩散速率越快,使得 PM2.5中重金属浓度的浓度也越低.金属浓度与SO2、NO2、PM2.5、CO呈显著正相关,这与这些污染物之间具有共同来源如工业排放、交通尾气、日常烹饪、生物质燃烧等[30-32]有关.近地层臭氧主要是由挥发性有机物、氮氧化物和一氧化碳在太阳光的作用下经过一系列复杂的光化学反应生成[33],温度越高,光辐射越强,O3浓度越高,而由于大气颗粒物扩散速率越快,大气颗粒物中重金属浓度也会下降,因此与O3呈负相关.
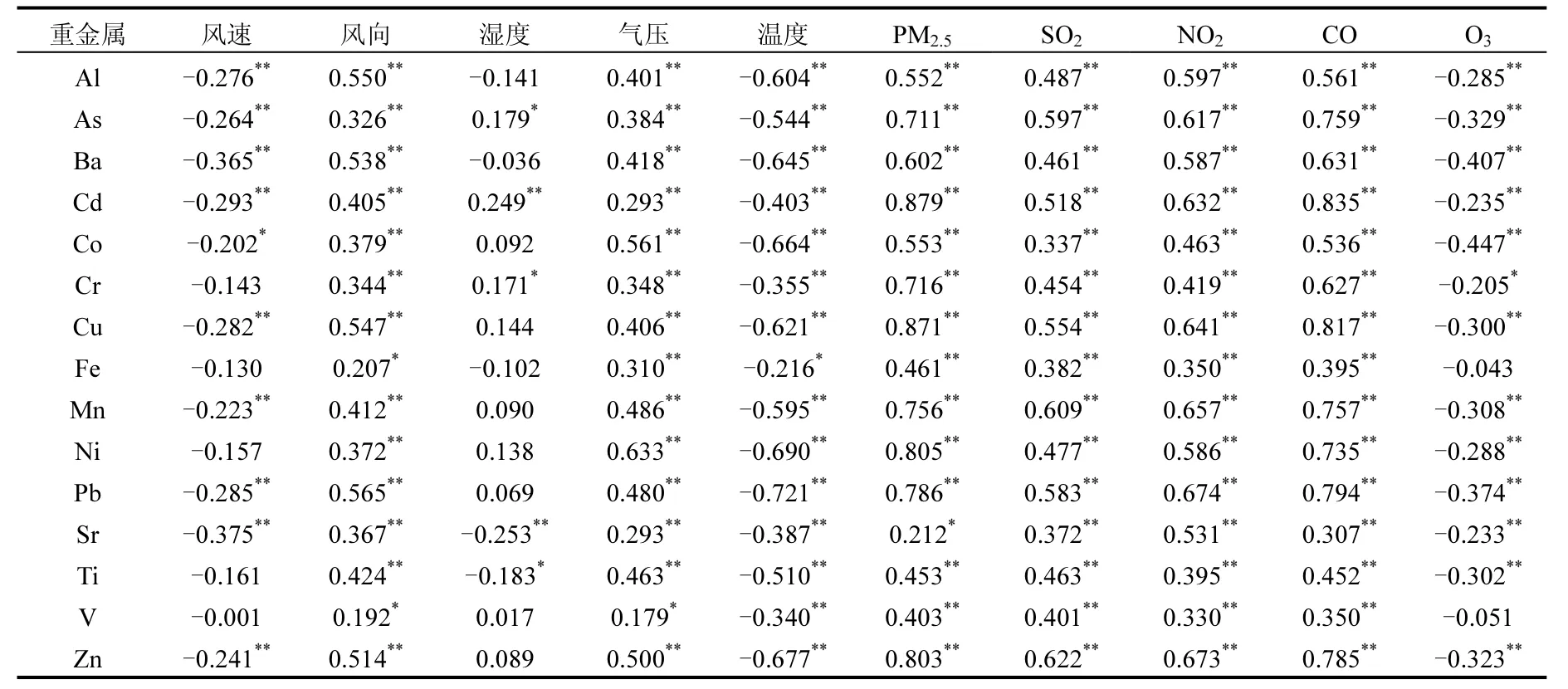
表3 PM2.5中重金属浓度与气象因子和大气污染物的皮尔逊相关系数(n=140)Table 3 Pearson’s correlation coefficients (r) between metal concentrations in PM2.5and meteorological factors/atmospheric pollutants(n=140)
2.4 数据主成分分析预处理
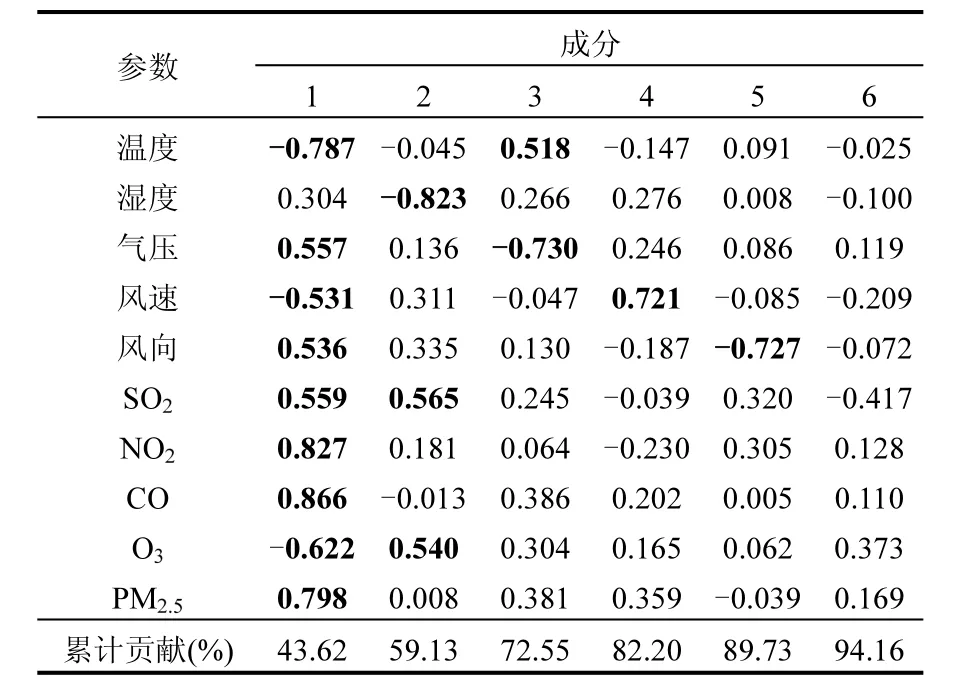
表4 主成分分析结果Table 4 Results of principal component analysis
如表4所示,前6个主成分的累计方差贡献比为 94.16%.温度、气压、风速、风向、SO2、NO2、CO、O3和PM2.5在第1个主成分上有较高载荷,这也说明各大气污染污染因子之间相关性较强.湿度、SO2、O3在第 2个主成分上有较高载荷,温度、气压在第3个主成分上有较高载荷,风速在第 4个主成分上有较高载荷,风向在第 5个主成分上有较高载荷.将原始数据做归一化处理并结合主成分构成系数核算出6个主成分,将其作为模型输入因子.
2.5 多元线性回归法的重金属模拟
多元线性回归法的金属模拟训练和验证的最佳相关系数如表5所示,大部分金属训练模型r值为0.7~0.9,对Pb和Zn训练模型的r值>0.9.验证模型的 r值排序为 Ni>Pb>Cu>Cd>Zn>Mn>Al>Ba>As>Co>Cr>Sr>Fe>Ti>V,其中前7种重金属模拟效果较好(r>0.8),后 4种模拟效果较差(r<0.6).鉴于《环境空气质量标准》[19]中Pb是常规监测指标,以Pb为例绘制模拟图(图2).
2.6 非线性数学方法的重金属模拟
2.6.1 BP神经网络法的重金属模拟结果 BPANN模拟训练和验证的最佳相关系数如表5所示,大部分金属训练模型r值保持在0.7~0.9之间.与MLR和SVM相比,除了Ba、Cr和V,BP-ANN对其他大部分金属训练模型的相关系数最高.验证模型 r值排序为 Cu>Cd>Pb>Ni>Zn>Mn>Al>As>Co>Ba>Sr>Ti>Cr>Fe>V,其中前 7种重金属模拟效果较好(r>0.8),后 3种重金属模拟效果相对较差(r<0.6). Pb监测值与模拟值的结果比对如图2所示.
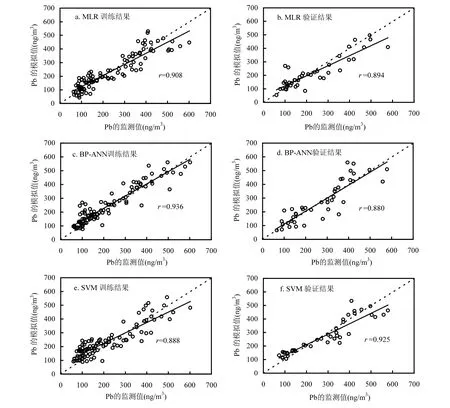
图2 多元线性回归、神经网络法及支持向量机对PM2.5中Pb浓度的模拟结果Fig.2 Simulation results of Pb concentrations in PM2.5by MLR,BP-ANN and SVM
2.6.2 支持向量机法的重金属模拟结果 SVM模拟训练和验证的最佳相关系数如表5所示,大部分金属训练模型r值保持在0.7~0.9之间,验证模型 r值排序为 Cd>Pb>Ni>Zn>Cu>Mn>As>Ba>Co>Al>Ti>V>Cr>Sr>Fe,所有金属浓度验证模型的 r值均>0.7.与 MLR和 BP-ANN相比, SVM 对所有金属验证模型的相关系数都最高. Pb监测值与模拟值的结果比对如图2所示.
2.7 讨论
BP-ANN对大部分金属元素(除了 Ba、Cr和V)训练模型的相关系数最高;而SVM对所有元素验证模型的相关系数最高,SVM对Cd、Pb、Ni、Zn、Cu、Mn模拟的验证相关系数甚至超过0.9,达到了强相关性.大气是复杂的非线性系统,使用非线性数学方法对污染物进行模拟评估具有一定优势.研究表明,SVM综合考虑了样本误差和模型复杂度[5,34],而BP-ANN结构难以确定,易陷入局部最优并引发维数灾难[35],因此,在处理小样本、高维度问题上,SVM往往比BP-ANN更有优势.
相关研究使用温度、湿度、NO、NO2等气象因子和污染物作为输入因子模拟大气污染物浓度,其结果显示,神经网络对 CO、O3、PM10、PM2.5验证模型的相关系数分别为0.8、0.8、0.65、0.75,支持向量机对O3、SO2、NO、NO2、CO、PM10验证模型的相关系数分别为 0.87、0.52、0.72、0.70、0.69、0.42[7,10,13,36].本研究训练模型和验证模型的相关系数大部分在 0.7~0.9之间,部分甚至超过0.9,可见所建立的PM2.5中重金属模拟模型具有一定的适用性和推广性.
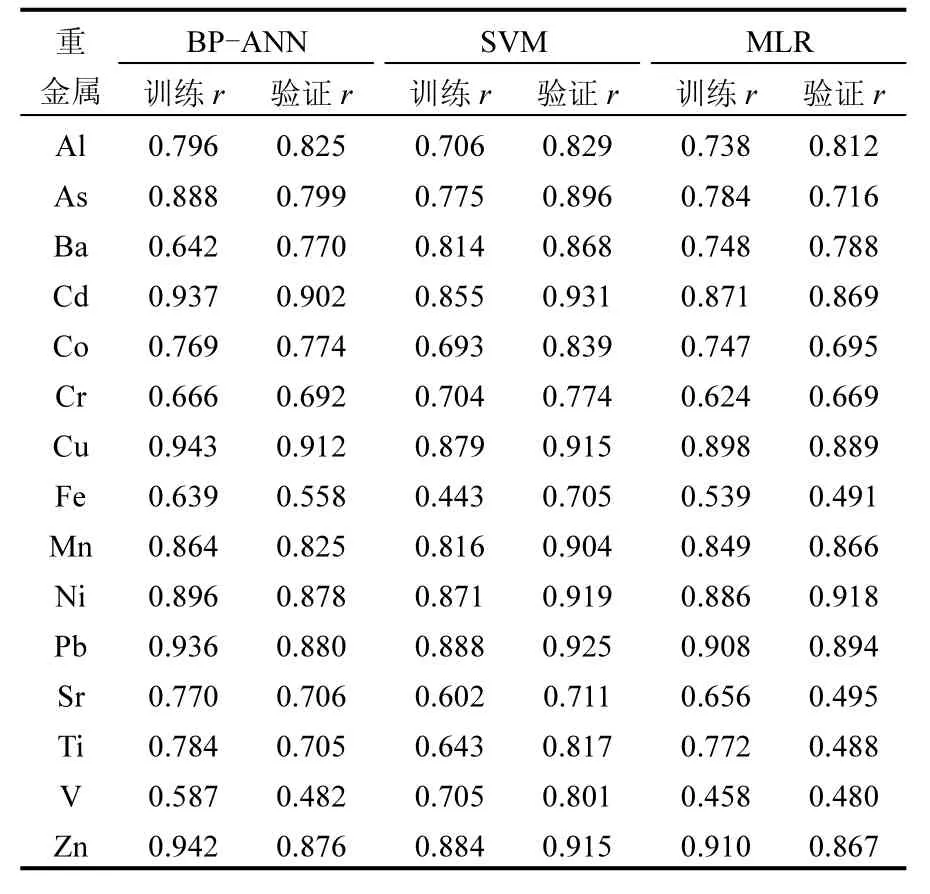
表5 模型模拟相关系数结果对比Table 5 Comparisons of correlation coefficients (r) between the three models
另外,3种方法对Cd、Cu、Pb、Ni和Zn的模拟结果都是最好的,而对Cr、Fe、Sr、Ti和V的模拟效果相对较差.根据作者以前的研究报道
[36], As、Cd、Cr、Cu、Ni和Pb主要来自于人为排放,而Al、Ba、Co、Fe、Mn、Sr、Ti和V主要来自于自然过程如土壤扬尘等.这些金属与输入因子特别是大气污染物之间的相关性存在较大差异,如:PM2.5、SO2、NO2、CO与Cd、Cu、Pb、Ni的相关性均明显高于Cr、Fe、Sr、Ti和V(表 3),这可能是影响其模拟效果的一个重要原因,而具体原理还需进一步验证.
3 结论
3.1 南京 PM2.5浓度及其中重金属在冬季最高,其次为春季,夏季和秋季浓度最低;PM2.5 中Fe、Al、Zn和Pb浓度较高,Cd、Mo和Co较低.与其他城市相比,南京大气重金属污染处于中等水平.
3.2 PM2.5中重金属与气压、SO2、NO2、PM2.5、CO呈显著正相关,与风速、温度和O3显著负相关,说明气象因素对 PM2.5中金属浓度具有不同影响;验证了大气重金属与气态污染物和 PM2.5之间具有显著相关性和共源性.
3.3 以主成分作为模型输入,非线性和线性数学方法对PM2.5中金属模拟的训练模型和验证模型的相关系数大部分在0.7 ~ 0.9之间;BP-ANN验证模型相关性系数大小:Cu>Cd>Pb> Ni>Zn>Mn>Al>As>Co>Ba>Sr>Ti>Cr>Fe>V>Mo;SVM验证模型相关性系数大小:Cd>Pb>Ni>Zn>Cu>Mn>As>Ba>Co>Al>Ti>V>Cr>Sr>Fe>Mo.总体上,使用非线性数学方法对大气重金属浓度进行模拟评估具有一定优势.
3.4 3种方法对Cd、Pb、Ni、Zn、Cu的模拟效果较好,SVM对这几种金属验证模型的r甚至高于0.9;而3种方法对Cr、Fe、Sr、Ti和V的模拟效果都相对较差.在缺乏充足数据情况下,采用非线性数学方法对PM2.5中重金属进行模拟是可行的.
[1] Mohanraj R, Azeez P A, Priscilla T. Heavy Metals in Airborne Particulate Matter of Urban Coimbatore [J]. Archives of Environmental Contamination & Toxicology, 2004,47(2):162-167.
[2] Bollati V, Marinelli B, Apostoli P, et al. Exposure to Metal-Rich Particulate Matter Modifies the Expression of Candidate MicroRNAs in Peripheral Blood Leukocytes [J]. Environmental Health Perspectives, 2010,118(6):763-768.
[3] Ghio A J. Biological effects of Utah Valley ambient air particles in humans: a review [J]. Journal of Aerosol Medicine, 2004,17(2): 157-164.
[4] Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators [J]. Neural Networks, 1989, 2(5):359-366.
[5] 瓦普尼克.统计学习理论的本质 [M]. 北京:清华大学出版社, 2000.
[6] Sait C. Sofuoglu, Aysun Sofuoglu, Savas Birgili, et al. Forecasting Ambient Air SO2Concentrations Using Artificial Neural Networks [J]. Energy Sources Part B Economics Planning& Policy, 2006,1(2):127-136.
[7] Martín M L, Turias I J, González F J, et al. Prediction of CO maximum ground level concentrations in the Bay of Algeciras, Spain using artificial neural networks [J]. Chemosphere, 2008, 70(7):1190-5.
[8] Hoffman S. Short-Time Forecasting of Atmospheric NOxConcentration by Neural Networks [J]. Environmental Engineering Science, 2006,23(4):603-609.
[9] 万显烈,杨凤林,王慧卿.利用人工神经网对空气中 O3浓度进行预测 [J]. 中国环境科学, 2003,23(1):110-112.
[10] Mckendry I G. Evaluation of artificial neural networks for fine particulate pollution (PM10and PM2.5) forecasting [J]. Journal of the Air & Waste Management Association, 2002,52(9):1096-101.
[11] Kukkonen J, Partanen L, Karppinen A, et al. Extensive evaluation of neural network models for the prediction of NO2, and PM10, concentrations, compared with a deterministic modelling system and measurements in central Helsinki [J]. Atmospheric Environment, 2012,37(32):4539-4550.
[12] Lu W Z, Wang W J. Potential assessment of the “support vector machine” method in forecasting ambient air pollutant trends [J]. Chemosphere, 2005,59(5):693-701.
[13] Sánchez A S, Nieto P J G, Fernández P R, et al. Application of an SVM-based regression model to the air quality study at local scale in the Avilés urban area (Spain) [J]. Mathematical & Computer Modelling, 2011,54(5/6):1453-1466.
[14] 于文革,王体健,杨 诚,等. PCA-BP神经网络在SO2浓度预报中的应用 [J]. 气象, 2008,34(6):97-101.
[15] 张徳丰. MATLAB神经网络应用设计 [M]. 北京:机械工业出版社, 2009.
[16] 邓乃扬.数据挖掘中的新方法 [M]. 北京:科学出版社, 2004.
[17] 杨卫芬,银 燕,魏玉香,等.霾天气下南京PM2.5中金属元素污染特征及来源分析 [J]. 中国环境科学, 2010,30(1):12-17.
[18] 张晓茹,孔少飞,银 燕,等.亚青会期间南京大气PM2.5中重金属来源及风险 [J]. 中国环境科学, 2016,36(1):1-11.
[19] GB18918-2002 环境空气质量标准 [S].
[20] 王 伟,孔少飞,刘海彪,等.南京市春节前后大气 PM2.5中重金属来源及健康风险评价 [J]. 中国环境科学, 2016,36(7):2186-2195.
[21] 杨勇杰,王跃思,温天雪,等.采暖期开始前后北京大气颗粒物中化学元素特征及来源 [J]. 环境科学, 2008,29(11):3275-3279.
[22] 王晴晴,马永亮,谭吉华,等.北京市冬季PM2.5中水溶性重金属污染特征 [J]. 中国环境科学, 2014,34(9):2204-2210.
[23] Chen J, Tan M, Li Y, et al. Characteristics of trace elements and lead isotope ratios in PM2.5from four sites in Shanghai. [J]. Journal of Hazardous Materials, 2008,156(1-3):36–43.
[24] 冯茜丹,党 志,黄伟林.广州市秋季PM2.5中重金属的污染水平与化学形态分析 [J]. 环境科学, 2008,29(3):569-575.
[25] Tao Y, Cheng X, Yang Z, et al. Distributional characteristics of heavy metal elements in atmospheric particulate matter and their impact on land quality in Liaoning province. [J]. Earth Science Frontiers, 2008.
[26] 李友平,刘慧芳,周 洪,等.成都市PM2.5中有毒重金属污染特征及健康风险评价 [J]. 中国环境科学, 2015,35(7):2225-2232.
[27] Lin H P, Xiao-Yan W U, Zhan J M, et al. Analysis of atmospheric particles and heavy metals character at the area of Lanzhou City in summer and winter [J]. Zhongguo Huanjing Kexue/china Environmental Science, 2012,32(5):810-815.
[28] Xu L, Chen X, Chen J, et al. Seasonal variations and chemical compositions of PM2.5, aerosol in the urban area of Fuzhou, China [J]. Atmospheric Research, 2012,104(1):264–272.
[29] Duan J, Tan J, Wang S, et al. Size distributions and sources of elements in particulate matter at curbside,urban and rural sites in Beijing [J]. Journal of Environmental Sciences, 2012,24(1):87-94.
[30] Fang G C, Wu Y S, Lee J F, et al. Characteristics and source identification study of ambient suspended particulates and ionic pollutants in an area abutting a highway [J]. Powder Technology, 2008,185(185):223-230.
[31] Juhos I, Makra L, Tóth B. Forecasting of traffic origin NO and NO2, concentrations by Support Vector Machines and neural networks using Principal Component Analysis [J]. Simulation Modelling Practice & Theory, 2008,16(9):1488-1502.
[32] Liao K J, Tagaris E, Napelenok S L, et al. Current and future linked responses of ozone and PM2.5to emission controls. [J]. Environmental Science & Technology, 2008,42(13):4670-5.
[33] Carpenter L J, Clemitshaw K C, Burgess R A, et al. Investigation and evaluation of the NOx/O3, photochemical steady state [J]. Atmospheric Environment, 1998,32(19):3353-3365.
[34] 陈 俏.支持向量机应用于大气污染物浓度预测 [D]. 西安:西安科技大学, 2010.
[35] 周 品. MATLAB神经网络设计与应用 [M]. 北京:清华大学出版社, 2013.
[36] Feng Y, Zhang W, Sun D, et al. Ozone concentration forecast method based on genetic algorithm optimized back propagation neural networks and support vector machine data classification [J]. Atmospheric Environment, 2011,45(45):1979-1985.
[37] Li H, Wang Q, Shao M, et al. Fractionation of airborne particulate-bound elements in haze-fog episode and associated health risks in a megacity of southeast China. [J]. Environmental Pollution, 2015,208:655-662.
致谢:本实验部分大气污染物数据由南京市环境监测中心站提供,在此表示诚挚的感谢!
Simulation of heavy metal concentrations in PM2.5based on nonlinear mathematics methods.
LENG Xiang-zi1, WANG Qin-geng1,2, QIAN Xin1,2*, LI Hui-ming1*, LU Hao1(1.State Key Laboratory of Pollution Control and Resources Reuse, School of the Environment, Nanjing University, Nanjing 210023, China;2.Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science & Technology, Nanjing 210044, China). China Environmental Science, 2017,37(3):821~828
Heavy metal concentrations were determined in PM2.5samples collected from Gulou and Pukou campus of Nanjing University in 2013. The pollution characteristics of heavy metals in different districts and different seasons were analysed, respectively. The correlations between heavy metal concentrations with meteorological factors or conventional air pollutants were investigated, respectively. The obtained data were pre-processed by principal component analysis, followed by the establishment of rapid evaluation models based on Back Propagation Artificial Neural Network (BP-ANN) and Support Vector Machine (SVM), respectively. Then models obtained from these two nonlinear mathematics methods were compared with those from multiple linear regression model (MLR). The results showed that PM2.5concentrations and the average heavy metal concentrations in PM2.5were all highest in winner, followed by spring, whereas the lowest in summer and autumn. The significant linear correlations were found between heavy metal concentrations with meteorological factors or air pollutant concentrations. BP-ANN showed the highest correlation coefficients of training models for most tested heavy metals (except for Ba, Cr, and V). SVM showed the highest correlation coefficients of verified models for all the tested heavy metals. All three methods showed good modelling effects on the evaluation of Cd, Cu, Pb, Ni, and Zn, but relatively poor modelling effects on the evaluation of Cr, Fe, Sr, Ti, and V.
PM2.5;heavy metals;back propagation artificial neural network;support vector machine;multiple linear regression
X513
A
1000-6923(2017)03-0821-08
冷湘梓(1992-),女,江苏宜兴人,南京大学硕士研究生,主要从事大气污染管理、环境模拟研究等.
2016-07-15
国家自然科学基金项目( 41271511,41501549)
* 责任作者, 钱新, 教授, xqian@nju.edu.cn; 李慧明, 博士, lihm0203@163.com
