基于弹丸激波的弹目偏差测试与反演研究

顾国华， 张良， 吴海兵， 崔逊学， 俞波

(陆军军官学院， 安徽 合肥 230031)

基于弹丸激波的弹目偏差测试与反演研究

顾国华， 张良， 吴海兵， 崔逊学， 俞波

(陆军军官学院， 安徽 合肥 230031)

由于空中超声速弹丸激波的复杂性和易被干扰性而难以捕捉，其弹目偏差测试是一大难题。为研究基于弹丸激波特性的弹目偏差测试原理和方法，在描述弹目偏差测试场景的基础上，分析激波形成机理和激波形成前后参数关系，建立弹目偏差测试模型和基于弹群激波环境简化的线性及非线性干扰模型。综合采用时间宽度测试原理进行外场试验与采用激波压力场累积效应的压力测试进行仿真反演相结合，结果表明仿真反演与工程测试相符合，为超声速运动目标声学定位和跟踪提供了一种新思路和方法。

兵器科学与技术； 弹道激波； 弹目偏差测试； 声场反演； 声压

0 引言

早在20世纪五六十年代学者们就对空中飞行物产生的激波理论进行了相关探索[1]，后来的研究[2-4]集中在对超音速飞行器环境和噪声影响的评估上。然而，由于激波干扰复杂、厚度难以感知、湍流不确定性等因素，常用数值模拟方法来探讨有关激波的空气动力学问题和飞机设计[5]。

当前，空中弹丸射击弹目偏差的测试方法主要有光电交汇、图像判读、雷达探测、声学探测、人工观测等[6]。这些方法各有优点和不足：1)光学交汇法的优点[7]是，实时性强、测量精度高、自动化程度高，不足[8]是视场交汇重叠区不能覆盖弹着点则无法测量，安装调试复杂，环境影响因素多；2)图像(录像)判读法的优点[9]在于，测量、存储方便直观，缺点[10]在于弹丸来自不同方向对精度影响大，难以实现实时成绩评定和报送；3)雷达探测法适用于大口径弹丸，小口径弹丸分辨率较差；4)声学探测法优点[11]在于定位精度高、安全性好，能实现全天候工作，不受光线和能见度影响，缺点是在复杂声场探测困难。前3种方法，还存在难以工作在弹群环境中，不能辨识重叠(弹丸相距很近)弹丸。

因而声学探测法具有其独特的优势。然而水下声探测研究成熟，空中声探测研究少；空中声标量探测研究较多，空中声矢量探测研究甚少。为发挥声学测试方法的优势，本文结合所在团队和前人多年在声学测试研究的基础上[12-16]，进一步研究空中激波环境中超音速弹丸的弹目偏差测试和仿真反演。在研究和分析弹丸弹目偏差解算时，为方便建立理论数学模型，进行了如下假设与简化：1)将“N”形波传播圆锥面理想化为2个几何上的圆锥面，未考虑激波厚度[17-18]；2)将有一定几何尺寸的传感器阵简化为一个点；3) 将一传感器到圆锥面距离近似简化为到其切平面距离；4) 仿真时将空气定为理想气体[19-20](绝热，传播均匀，未考虑风速、气温等影响)；5) 拖靶飞行速度为匀速；6) 其他理想化的因素。这些因素值得继续深入研究和细化。

1 弹道激波形成

弹道激波是弹丸以超音速飞行时产生的一种非线性大气声学现象。如图1所示，弹丸飞出炮口后，以超音速飞行时，前方的空气被挤压来不及向外扩散而形成一定程度的高压；而弹丸后方的空气被排开而膨胀，形成较为突然的负压。大气中压缩区(高压区)和膨胀区(负压区)结合起来，产生了空气动力学中的凹角转折和凸角转折现象，便在弹头、弹带和弹尾部形成近似圆锥形的稠密空气层，就形成弹道激波，同时，在弹尾底部后面呈现低真空的涡流区。该现象在空气动力学中称为激波(也称声爆)，在弹道学中分别称为弹头波、弹带波和弹尾波，统称为弹道波[21]。

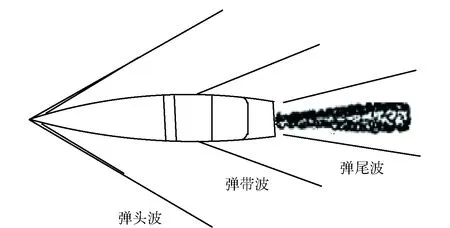
图1 弹丸飞行产生的弹道波Fig.1 Ballistic shock wave of flying projectile

空气的压缩或膨胀使空气流波形变陡，其过程实际上气体的压力、密度、温度和速度等空气参量的微扰动迅速累积而产生突变。显然，激波具有一定厚度，可用空气分子的自由行程加以计量，此处略。为更方便分析激波产生前后空气参数的变化，认为激波是一种不连续面，忽略其厚度[22]。

弹丸产生的激波在空气中向四周传播，由于空气介质的非均匀性(声阻、气温、风)，使得非线性因素产生累积效应，激波中的高压区传播速度快于声速，而激波的低压区传播则低于声速。传播时使得弹丸激波高压区和低压区容易形成一个渐进的外形，形似英文字母“N”，所以通常又将其称为“N”形波。

弹丸激波的形成大体上可由4个过程来描述[11]，如图2所示。弹丸头部锥体形成的凹角转折使压力从常压p0急速上升至p0+p1，锥柱界面形成的凸角转折使压力从p0+p1降至p0，柱面膨胀又使压力从p0渐降至p0-p2，弹丸底端的界面变化又使压力从p0-p2急速回升至p0. 图2中，TF为激波时间宽度，ti为砰发点时刻，τ1、τ2为前后沿上升时间。

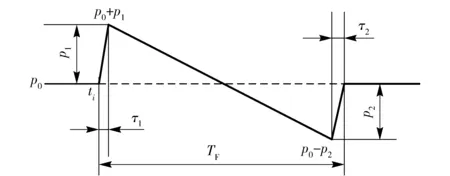
图2 “N”形波Fig.2 “N”shock wave

经进一步研究表明，理想“N”形波前后沿上升时间τ1=τ2，幅值p1=p2.

2 弹目偏差测试场景与激波声场

2.1 弹目偏差测试场景

当弹丸从靶标附近飞过，其弹道距靶心的最短距离称为弹目偏差(也称脱靶量)。其基本场景和主要参数关系如图3所示。可知理论上弹目标偏差可表示为dcosμ(d为“N”形波传播距离)，而现实中由于炮弹、拖靶、探测器阵都在运动，以及环境、气象等因素影响，实时情况非常复杂，而给理论模型和工程实践带来了难度。

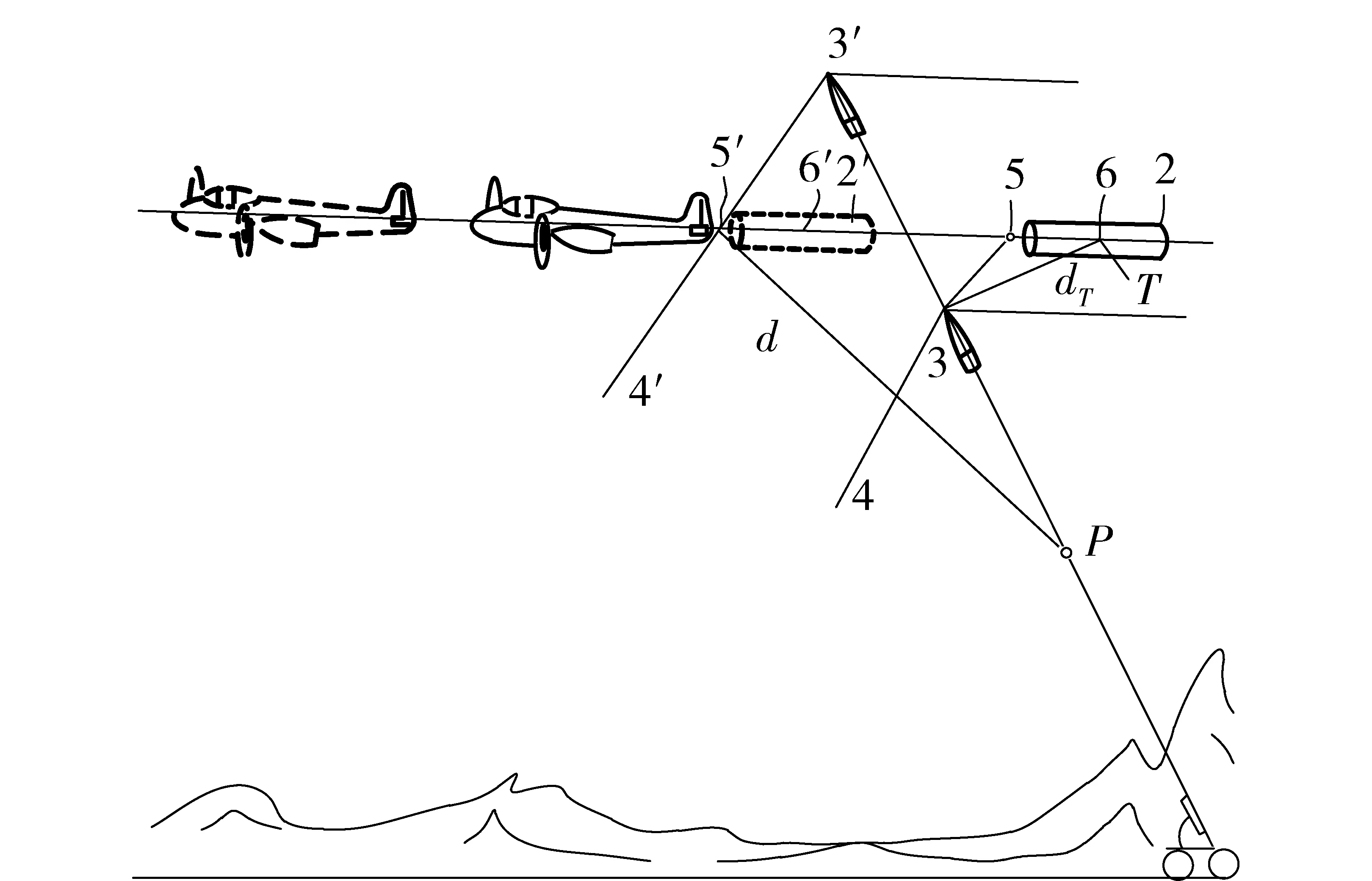
图3 弹目偏差向量测试原理Fig.3 Test principle of vector miss distance

当弹丸向拖靶发射时，通常瞄向其靶心的未来点。当弹丸运到某一位置P点时，“N”形波前沿4以平行于线d的方向传播。当弹丸到达3′位置时“N”形波前沿4′到达靶前部探测器5′，此时靶在位置2′，在P点产生的“N”形波将遇见在位置5′的探测器，将P点称作砰发点。

由于“N”形波传输到传感器期间自身的运动和靶的运动，因而P到“N”形波接收点的距离并不是弹目偏差距离。图3中用实线表示的拖靶是弹丸在位置3时距其最近时所处的位置，此时弹丸3到靶心T的距离(位置6)dT即为弹目偏差距离。

由于实践测试的困难性，工程上是通过测量的“N”形波时间宽度来计算dT的。

2.2 运动声场激波前后关系分析

为进行试验反演，首先对激波前后参数关系进行建模[22-24]分析，描述弹丸激波前后关系如图4所示。将超音速弹丸(速度vb)运动转化为超音速来流状态。产生激波前，来流为vb，气流速度沿弹丸切线方向分量vbt，气流速度沿弹丸法线的方向分量vbn；产生激波时，激波倾角为β；产生激波后，气流的切线分量为vat，法向分量为van，激波转折角为ω.

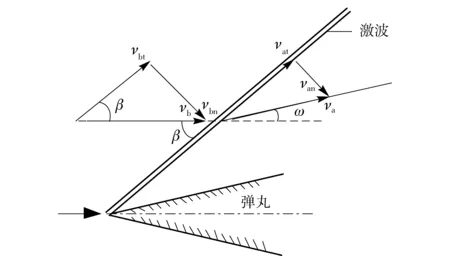
图4 激波前后参数关系Fig.4 Parameter relations before and after shock wave forming

由克拉珀龙方程得

(1)

式中：k为热容；ρ表示气体密度，ρb为激波产生前空气密度，ρa为激波产生后空气密度；p为单位体积空气压力，pb为激波产生前空气压力，pa为激波产生后空气压力；m为单位空气质量；M为气体摩尔质量；R为气体常量；vs为考虑热消耗时激波产生后的速度；c0为理想状态空气声速。

由能量守恒，激波产生前后认为空气是绝热的，以及由激波前后的质量流量相等原理，求解(1)式，可得

(2)

(3)

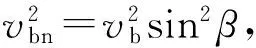
(4)

(5)

式中：Mab为激波产生前气流的瞬时马赫数。

根据能量方程及郎金- 雨贡纽关系式，有

(6)

(7)

在空气中，气流通过激波时可认为总温度保持不变，有

(8)

至此，可建立激波产生前后的迭代关系，为解算弹目偏差提供试验理论依据。

3 弹目偏差测试基本模型

所谓弹目偏差是指火炮在瞄准靶射击过程中，弹丸飞经靶附近时距靶心的最短距离[12]。为提高脱靶量测试精度和判别射弹散布区域，工程实现是采用了4个声传感器Mi(i=1,2,3,4)并组成一个阵列，布置在一个平面上，每个传感器代表一个象限，方位信息则通过首遇“N”形波的传感器得到，如图5所示，图中vt为拖靶运动方向。

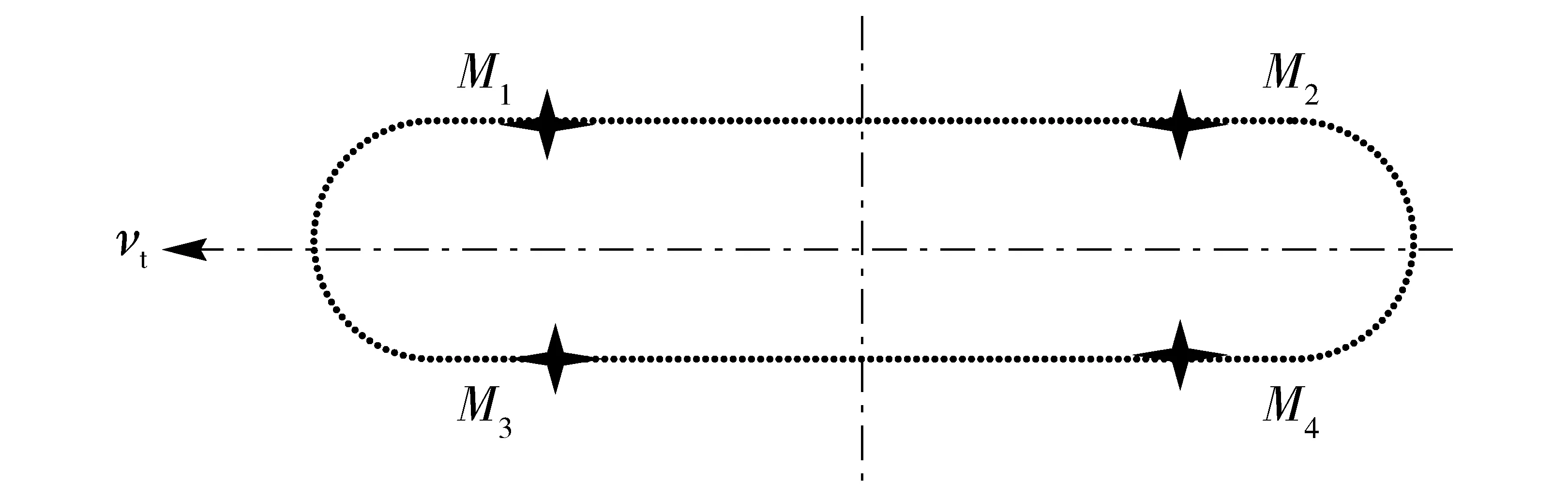
图5 传感器布局示意图Fig.5 Layout diagram of sensors

传感器M1和M2、M3和M4分别为一组，用于误差修正。用4个传感器检测和计算脱靶距离R，弹目偏差各参量关系如图6所示。

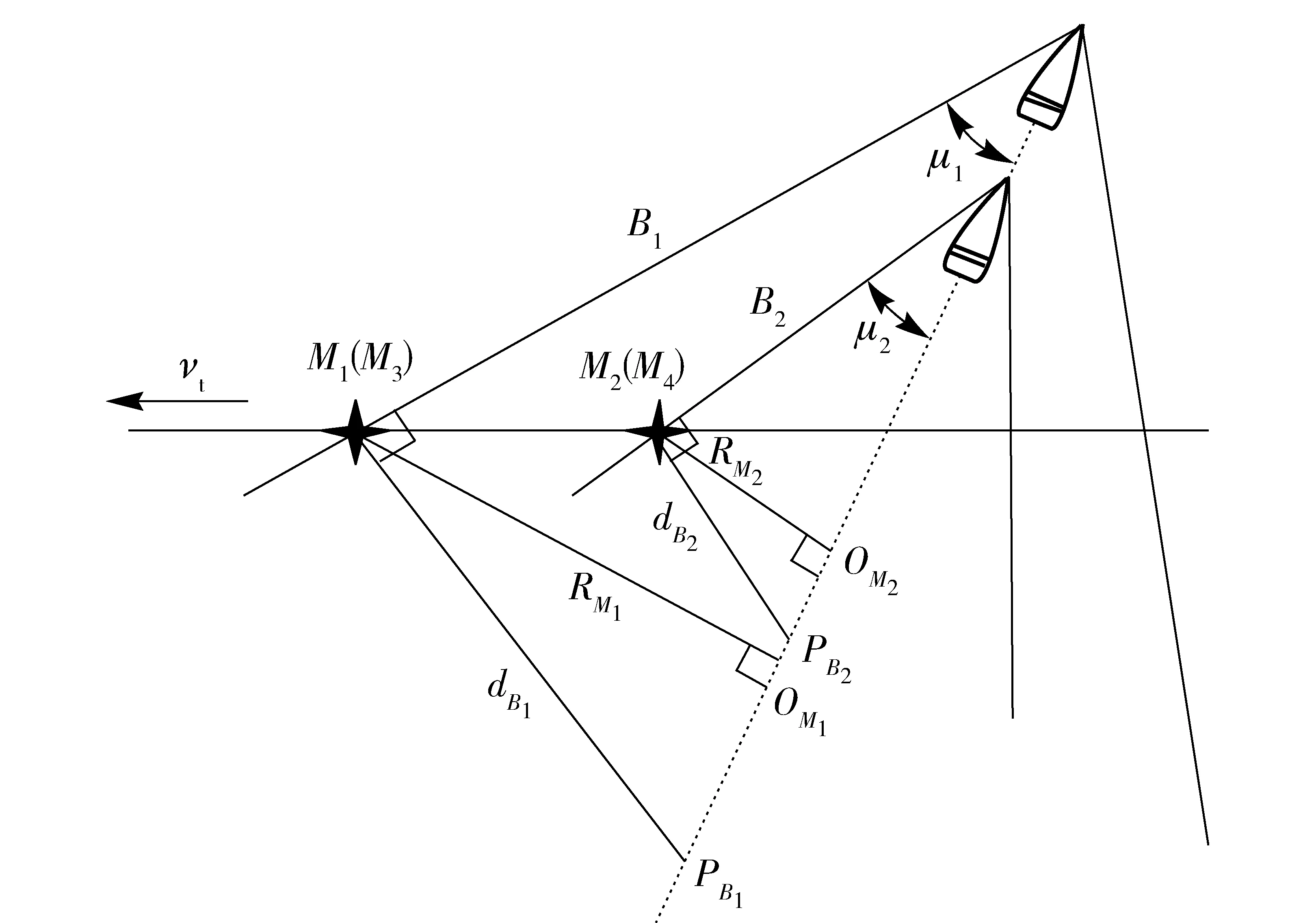
图6 弹目偏差各参量关系图Fig.6 Parameter relations of miss distance

根据sinμ=c0/vp=1/Ma，有

(9)

式中：vp为弹丸速度。

第1节中指出，弹丸激波为一圆锥面，为更好分析激波传播情况，确定任意时刻激波参数，根据Whitham理论在文献[16]基础上建立激波面模型：

(10)

式中：A(r)为激波某区域的面积，r为区域半径；uf为气流速度。由(10)式可推导出：

1.1.2 父本来源。父本由皖芝2164 Co60辐射诱变系选，单秆型，一般株高160 cm。叶绿色，白花，一叶三蒴，蒴果四棱，单株蒴果数82.5个。始蒴部位较低，中长果型，结蒴较密，每蒴粒数60.8粒左右，千粒重3.02 g，种皮白色。耐旱性较强，抗枯萎病。正常夏播全生育期90 d左右。2013年参加安徽省区试，平均产量为1 479.0 kg/hm2，比豫芝4号增产0.68%。2014年通过安徽省鉴定。

(11)

(12)

根据速度势[25]

(13)

求出推迟时间可表示为

(14)

式中：R为有效辐射半径；Q0为声源原始强度；Ma0为声源原始马赫数；ct为声源传播速度；x为接受点处位置，y为声源在传播方向所处位置；x1、x2、x3分别为某3个位置接收点。

激波面上有

(15)

式中：ρ0为声源处空气原始密度。

因而，超声速声源传播(辐射)距离可表示为(根号前取正号)

(16)

(17)

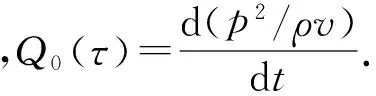
至此，可解算出任意时刻，激所处的位置极其压力。

4 弹群激波干扰分析

(18)

式中：U、V为激波在x、y方向上的速度；E为单位质量气体总能量；u、v为弹丸在x、y方向上的速度；Θx、Θz为x、z方向上张力瞬态值；τxx、τzz、τxz、τzx为黏性应力张量在不同方向上的分量。

假设在扰动情况下，流场矢量q的扰动前为q0，扰动量为q′，则q=q0+q′，扰动的通量包含了非线性的扰动项。在忽略了扰动黏性项后，可对(18)式进行分析，将扰动分为线性和非线性扰动。设ρ0、p0、u0、v0、e0分别是密度、压强、速度以及总能量的各方向平均量，其对应的扰动量分别为ρ′、p′、u′、v′、e′；E0为总能量，对应的扰动量为E′.

1)当为线性扰动时，有

(19)

2)当为非线性扰动时，有

(20)

由完全气体的状态方程(γ为比热比)，E可表示为

5 外场试验

为验证模型的有效性和系统功能，在某试验场进行了野外试验。工况为：地面立靶2 m×2 m，靶中心高出地面2.4 m，靶面下边缘离开地面1.4 m. 现场布置示意图如图7所示。

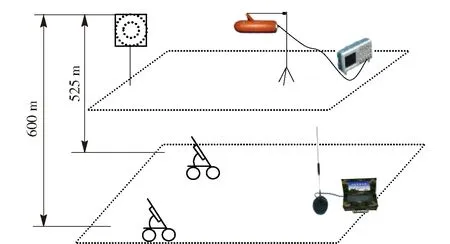
图7 外场试验布置Fig.7 Field test arrangement

5.1 现场布置

试验仪器包括，指示器(2传感器系统和4传感器系统各一套)、地面站主机、示波器及打印机等。

设置A型炮射击距离为525 m、B型炮射击距离为600 m，指示器先后放在距靶心5 m、10 m、

15 m、20 m、25 m、30 m、35 m的位置上，在每一处接收3发能同时测到弹丸存速的原始数据，并测量出M1到靶洞的脱靶距离。

调整指示器支架使传感器M1、M2、M3和M4在同一平面上，且上面两传感器与下面两传感所在直线平行。调整指示器使指示器平面与立靶平面在同一平面上。

试验所采用的弹目偏差的经验公式[12,15]，即

(21)

式中：C1、C2为校准系数。

5.2 试验数据

I型高炮某试验场的部分试验数据见表1.

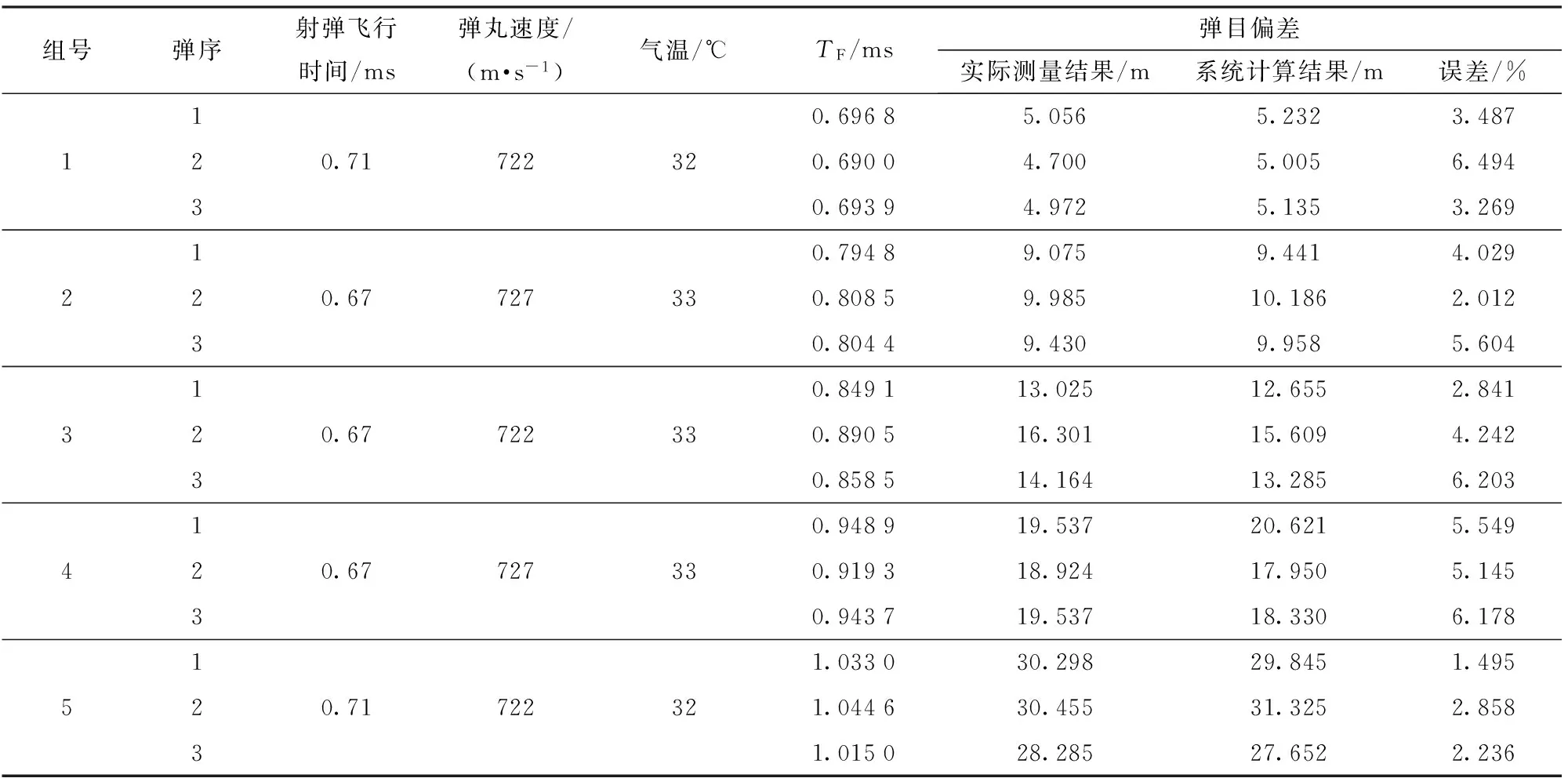
表1 A型高炮部分试验数据Tab.1 Some experimental data of antiaircraft gun A

注：指示器采用4传感器系统，炮目距离为550 m，指示器位于靶平面前侧3 m.

采用Levenberg-Marquardt法和通用全局优化法进行拟合，得出：均方根误差(RMSE)为0.666 346 546，残差平方和(SSE)为6.660 265 800，相关系数R为0.997 007 629，相关系数之平方R2为0.994 024 213，决定系数(DC)为0.993 966 89，Chi-Square系数为0.207 317 434， F-Statistic统计为2 162.445 651. 结果得出C1=253.902，C2=30.884. 实测试验数据与拟合的理论数据线曲线与如图8所示，误差如表1所示。精度较高，符合系统测试需求。

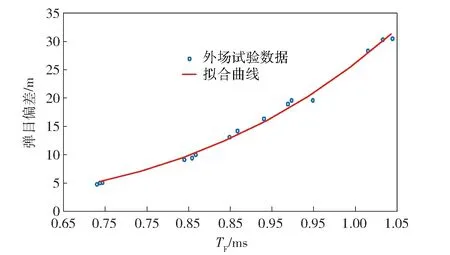
图8 外场试验数据点分布拟合图Fig.8 Field test data points and their fitted curve

6 仿真反演与分析

为了验证模型和方法的有效性，对2发超声速弹丸邻近干扰情况进行了仿真模拟和计算。初始条件来流为理想空气，Ma=2.12，静压为101 325 Pa，来流静温为103.2 K，弹丸攻角为3°，通过计算流体力学(CFD)软件计算结果如图9～图13所示。

残差结果如图9所示，空气密度分布等值图如图10所示，弹丸I、弹丸II压力分布如图11所示，图12为上下边界所受的压力图。

图9 残差曲线图Fig.9 Residual error plot

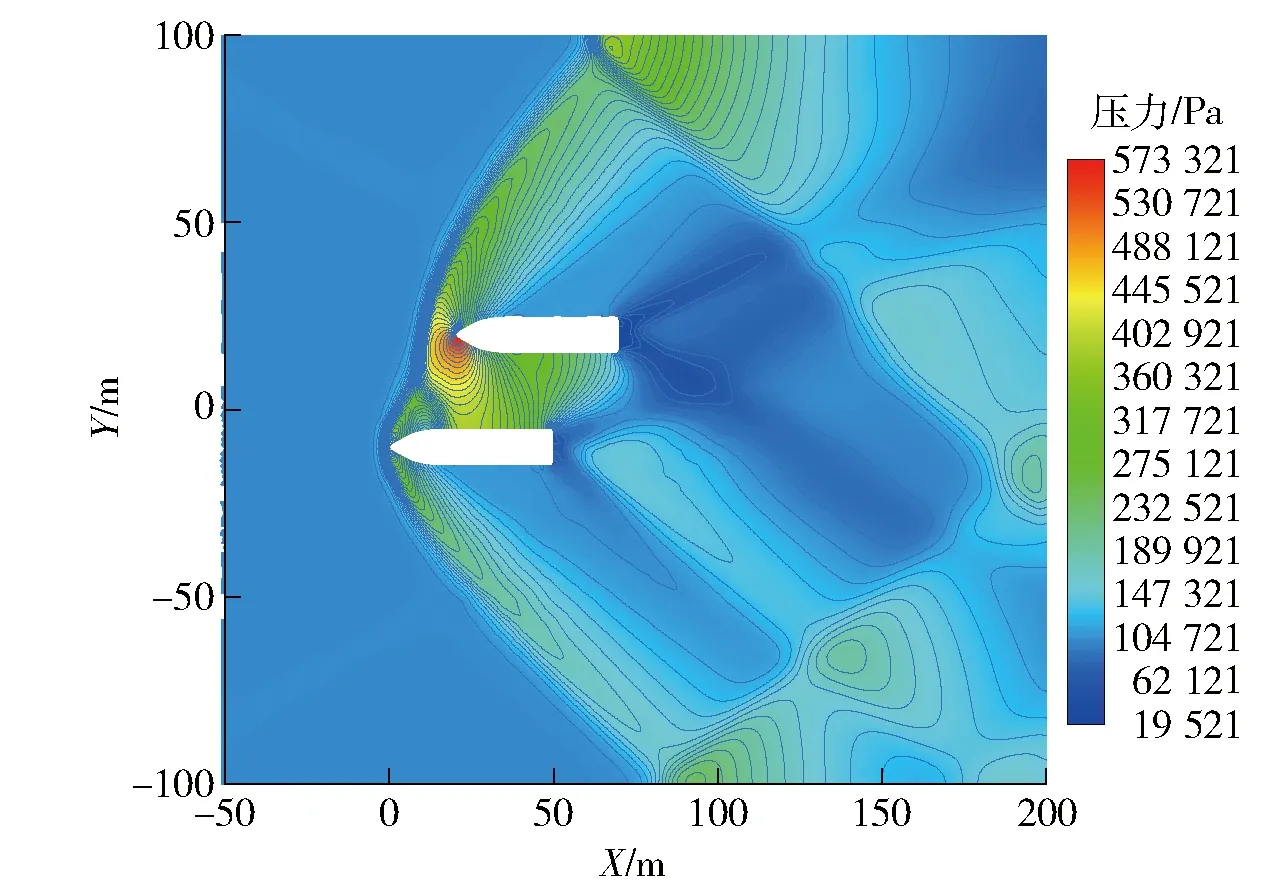
图10 压力分布等值图Fig.10 Pressure distribution contour map

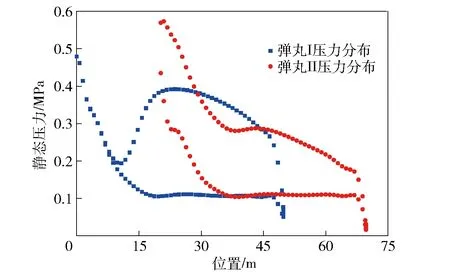
图11 弹丸Ⅰ与弹丸Ⅱ压力分布图Fig.11 Pressure profile of Projectile Ⅰ and Projectile Ⅱ

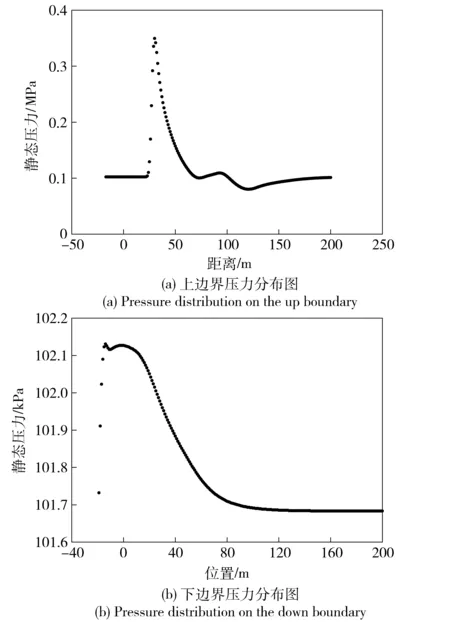
图12 边界压力分布图Fig.12 Pressure distribution at boundary

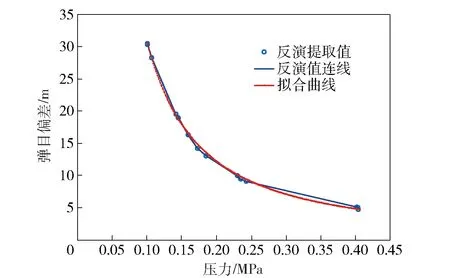
图13 仿真拟合数据Fig.13 Simulated data and its fitted curves

通过计算仿真，根据弹丸飞行参数，对指示器在距靶心5 m、10 m、15 m、20 m、30 m的位置上抽取每组3项弹丸的压力幅值如表2所示。

通过压力解算得出反演的弹目偏差，采用粒子群算法，拟合结果如图13所示。得出：RMSE为0.302 236 05，SSE为1.370 199 46，R为0.999 458 7，R2为0.998 917 66，DC为0.998 758 82，Chi-Square系数为0.056 691 626，F-Statistic统计为1 997.941 786，将弹目偏差结果与实测比较，得出误差小于5%，压力幅值反演误差小于4%.

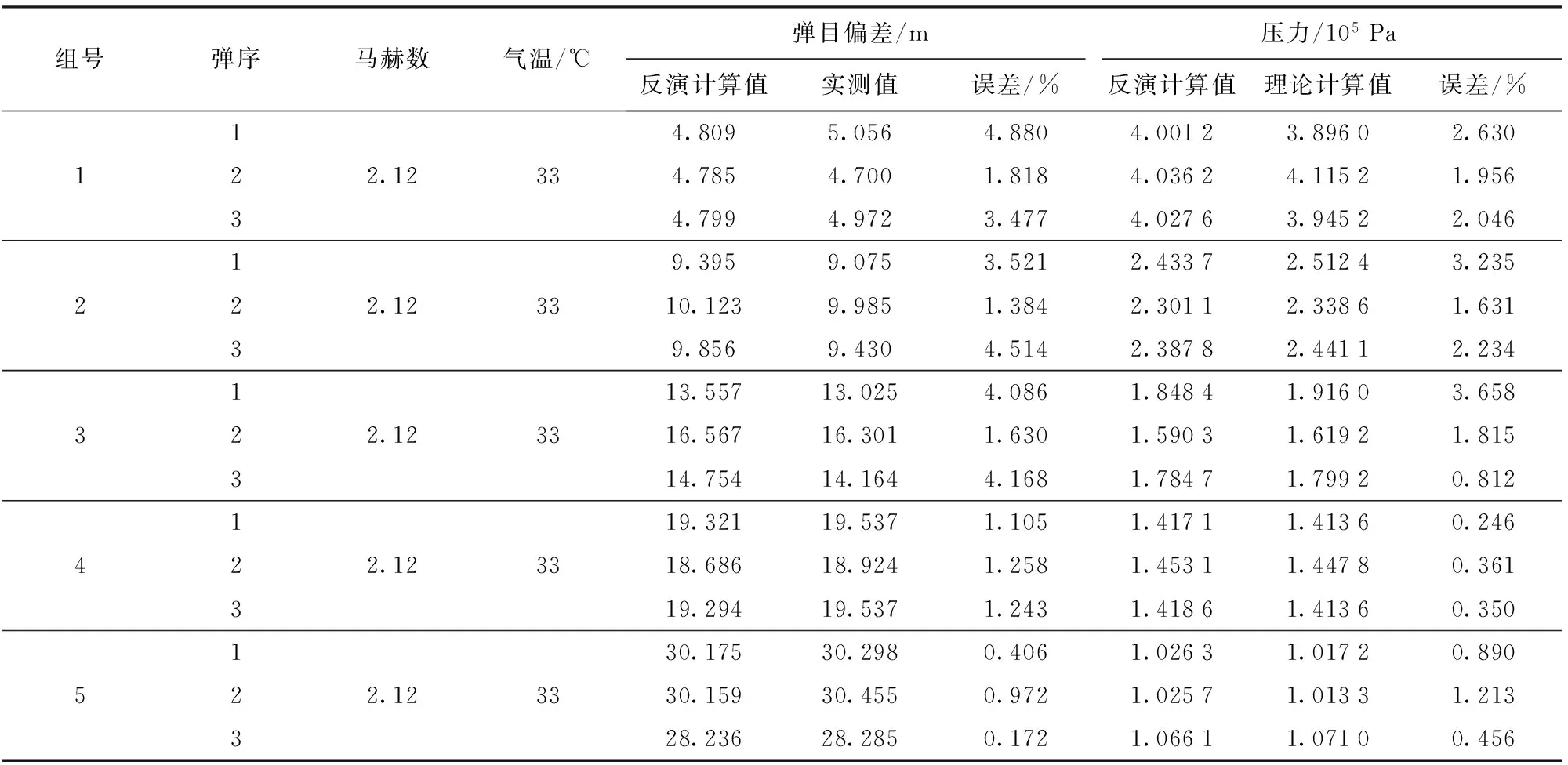
表2 仿真反演数据及误差Tab.2 Inversion data and its errors

注：仿真反演计算时忽略弹速、气温的微小差别。

7 结论

仿真反演是气动声学研究的重要手段，通过数值仿真和外场试验的结合能更有效地检验理论研究，优化工程应用效果。

1)实测试验数据与拟合的理论数据表明基于弹丸激波的弹目偏差测试精度较高，误差为7%以内，符合实际需求。

2)对2发超声速弹丸邻近干扰情况进行了仿真模拟和计算表明，采用压力解算仿真反演得出的弹目偏差与外场试验接近，得出距离误差小于5%，压力幅值反演误差小于4%.

研究结果表明，仿真反演与工程测试相符，方法可行，为超声速运动目标声学定位和跟踪提供了一种新思路和方法。

References)

[1] DV Gaitonde. Progress in shock wave/boundary layer interactions[J]. Progress in Aerospace Sciences,2013(72):80-99

[2] Libal U, Spyra K. Wavelet based shock wave and muzzle blast classification for different supersonic projectiles[J]. Expert Systems with Applications, 2014, 41(11):5097-5104.

[3] Heimbs S, Ritzer J, Markmiller J. A numerical method for blast shock wave analysis of missile launch from aircraft[J]. International Journal of Aerospace Engineering, 2015, 2015:1-8.

[4] Aswin G, Chakraborty D. Numerical simulation of tansverse side jet interaction with supersonic free stream[J]. Aerospace Science and Technology, 2010, 14(5):295-301.

[5] 杨训仁, 陈宇. 大气声学[M]. 北京:科学出版社, 2007:256-257. YANG Xun-ren, CHEN Yu. Atmospheric sound[M]. Beijing:Science Press, 2007:256-257.(in Chinese)

[6] 国蓉, 何镇安, 王伟. 被动声探测技术与弹着点定位方法综述[J]. 电声技术, 2010, 34(11):48-49. GUO Rong, HE Zhen-an, WANG Wei. Review of passive acoustic localization technique and impact point location methods[J]. Elementary Electroacoustics, 2010, 34(11):48-49.(in Chinese)

[7] 于雪媛, 左乾县, 李永锋. 一种测试弹丸落炸点的数学模型[J]. 火炮发射与控制学报, 2008(4):123-126. YU Xue-yuan, ZUO Qian-xian, LI Yong-feng. A mathematical model of gun ball fall explosion point measurement[J]. Journal of Gun Launch & Control，2008(4):123-126.(in Chinese)

[8] 王英, 曾光宇. 双线阵CCD交汇测量立靶精度系统研究[J]. 光电工程, 2011, 38(10):33-38. WANG ying, ZENG Guang-yu. Intersection measuring system of erecting target with dual liner CCD[J]. Opto-Electronic Engineering, 2011, 38(10):33-38.(in Chinese)

[9] 张先叶, 高俊钗, 李亚强. 弹丸立靶坐标的图像处理算法研究[J]. 科学技术与工程, 2008, 8(11):3018-3021. ZHANG Xian-ye, GAO Jun-cha, LI ya-qiang. Image processing algorithm of the pill coordinates[J]. Seience Technology and Engineering, 2008, 8(11):3018-3021.(in Chinese)

[10] 田会, 倪晋平, 鲁倩, 等. 光幕与图像融合式自动报靶系统[J]. 西安工业大学学报, 2012, 32(8):617-621. TIAN hui, NI jin-ping, LU qian, et al. Automatic target scoring system based on light screen and image porcessing[J]. Journal of Xi’an Technological University, 2012, 32(8):617-621.(in Chinese)

[11] 顾国华, 陈栋, 王彩, 等. 基于声学靶传感器的弹着点测试研究与实现[J]. 电子测量技术, 2007, 30(2): 154-156. GU Guo-hua, CHEN Dong, WANG Cai, et al. Research and implement of acoustics testing impact points based on target sensor[J]. Electronic Measurement Technology, 2007, 30(2):154-156.(in Chinese)

[12] 张飞猛, 马春茂. 对空射击声学靶脱靶量测试系统的精度分析[J]. 兵工学报, 2000, 21(1):23-26. ZHANG Fei-meng, MA Chun-mao. Accuracy analysis for the measuring system of target deviation for projectiles shooting an acoustic target[J]. Acta Armamentarii, 2000, 21(1):23-26.(in Chinese)

[13] 张飞猛, 徐长根. 高炮射击效果实时评价系统测量误差修正[J]. 测试技术学报, 2007, 21(6):505-509. ZHANG Fei-meng, XU Chang-gen. Test error revision of real time evaluation system for anti-aircraft firing effect[J]. Journal of Test and Measurement Technology, 2007, 21(6):505-509.(in Chinese)

[14] Levin D, Gannot S, Habet S. Direction-of-arrival estimation using acoustic vector sensors in the presence of noise[C]∥2011 IEEE International Conference on Acoustics, Speech and Signal Processing. Prague, CZ:IEEE, 2011:105-108.

[15] 张飞猛. 火炮对悬吊靶射击的脱靶向量测试系统[J]. 测试技术学报, 1999, 13(1):28-31. ZHANG Fei-meng. The missing target vector measurement system of the hang targets fired by the gun[J]. Journal of Test and Measurement Technology, 1999,13(1):28-31.(in Chinese)

[16] 吴寿荣. 球面激波对平面的马赫反射的简化处理[J]. 空气动力学报， 1990(4):480-481. WU Shou-rong. Simple disposal of mach reflection of spherical shock wave on a plane[J]. Acta Aerodynamica Sinica, 1990(4):480-481.(in Chinese)

[17] Wagner B, Schmidt W. Theoretical investigations on shock wave-boundary layer interaction in cryogenic nitrogen[J]. Springer International Publishing, 2015, 365(3):341-350.

[18] 陶如意, 王浩, 赵润祥. 超音速子母弹分离激波干扰特性研究[J]. 兵工学报, 2011, 32(10):1206-1211. TAO Ru-yi, WANG Hao, ZHAO Run-xiang, et al. Research on shock/shock wave disturbance characteristics in separation of supersonic cluster munition[J]. Acta Armamentarii, 2011, 32(10):1206-1211.(in Chinese)

[19] Kremeyer K . Energy deposition systems, equipment and method for modifying and controlling shock waves and supersonic flow: US, 8960596B2[P].2015-2-24.

[20] Lombard B, Matignon D, Gorrec Y L. A fractional Burgers equation arising in nonlinear acoustics: theory and numerics[J]. IFAC Proceedings Volumes, 2013, 46(23):406-411.

[21] 王东生. 炮口波、弹道波、爆炸波[J]. 兵器知识, 1985(3):23. WANG Dong-sheng. Muzzle wave, ballistic wave and blast wave[J]. Ordnance knowledge, 1985(3):23.(in Chinese)

[22] 王南炎. 弹丸空气动力学[M]. 南京:中国人民解放军总字150部队, 1962:148-155. WANG Nan-yan. Projectile aerodynamics lecture [M]. Nanjing:Unit 150 of PLA, 1962:148-155.(in Chinese)

[23] 王保国. 空气动力学基础[M]. 北京:国防工业出版社, 2014:122-123. WANG Bao-guo. Aerodynamics basis[M]. Beijing:National Defense Industry Press, 2014:122-123.(in Chinese)

[24] Gnani F, Lo K H, Zare-Behtash H, et al. Shock wave diffraction in the presence of a supersonic co-flow jet[J]. Shock Waves, 2016, 26(3):1-10.

[25] 张强. 气动声学基础[M]. 北京:国防工业出版社，2012：145-147. ZHANG Qiang. Aeroacoustics foundation[M]. Beijing:National Defense Industry Press, 2012:145-147.(in Chinese)

[26] 张金明. 气动声学数值计算的算法研究[D]. 南京:南京航空航天大学, 2009:6-8. ZHANG Jin-ming. Research of numerical method for computational aeroacoustics[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2009:6-8.(in Chinese)

[27] Sofronov I L. Non-reflecting inflow and outflow in a wind tunnel for transonic time-accurate simulation[J]. Journal of Mathematical Analysis & Applications, 2010, 221(1):92-115.

Research on Miss Distance Test Based on Projectile Shock Wave and Its Inversion

GU Guo-hua, ZHANG Liang, WU Hai-bing, CUI Xun-xue, YU Bo

(Army Officer Academy, Hefei 230031, Anhui, China)

Since the shock wave of supersonic projectile is difficult to be captured due to its complexity and susceptible interference, the miss distance test is a difficult problem. The testing scene of miss distance is described, the formation mechanism of shock wave is analyzed, and the parameter relations before and after shock wave forming are identified. The test model of miss distance and the linear and nonlinear interference models based on simplified shock wave environment are established. The time duration test principle is used for field experiment, and the cumulative effect of pressure of shock wave field is used for simulating inversion in order to verify the accuracy and effectiveness of test methods and engineering test.

ordnance science and technology; ballistic shock wave；miss distance；acoustic field inversion; acoustic pressure

2016-06-03

国家自然科学基金项目(61672532)

顾国华(1981—)，男，博士研究生。E-mail:Lmonkey2010@sohu.com

崔逊学(1969—)，男，教授，硕士生导师。E-mail：xxcui@tsinghua.org.cn

TJ011+.2

A

1000-1093(2017)03-0576-09

10.3969/j.issn.1000-1093.2017.03.022