轴向柱塞泵回程球铰副油膜润滑压力形成机理研究
2017-04-11王涛毛明唐守生盖江涛冀海
王涛, 毛明, 唐守生, 盖江涛, 冀海
(1.中国北方车辆研究所 车辆传动重点实验室, 北京 100072; 2.北京理工大学 北京电动车辆协同创新中心, 北京 100081)
轴向柱塞泵回程球铰副油膜润滑压力形成机理研究
王涛1,2, 毛明1,2, 唐守生1, 盖江涛1,2, 冀海1
(1.中国北方车辆研究所 车辆传动重点实验室, 北京 100072; 2.北京理工大学 北京电动车辆协同创新中心, 北京 100081)
回程球铰副是应用于轴向柱塞变量泵的机械结构,为研究其空间相对运动特征,结合回程球铰副的几何特征与相对运动关系,提出基于柱面特征的油膜润滑机理分析模型。通过拓展经典JFO空化算法以考虑复杂表面剪切速度影响因素,建立回程球铰副油膜润滑数值分析方法;对比分析斜盘倾角7.5°、12.5°与17.5° 3种典型工作条件下的润滑状态,以及摩擦副表面剪切速度分布、间隙形状分布、空化指数分布和压力分布之间的关系。研究结果表明:间隙形状引起的动压效应与表面剪切速度引起的伸缩效应共同决定油膜压力场具有“双峰双谷”的分布规律,伸缩效应与斜盘的倾斜程度呈正相关性,是导致润滑承载力下降的重要因素;回程球铰副润滑设计需综合考虑伸缩效应与动压效应对油液成膜过程的复合影响。
兵器科学与技术; 柱塞泵; 回程球铰副; 动压润滑; JFO空化算法; 油膜空化
0 引言
轴向柱塞变量泵,具有工作压力高、功率密度大及排量改变方便等优点,目前被广泛应用于车辆与行走机械的静液驱动系统[1-2]。在以往的研究中,由于柱塞- 缸体、滑靴- 斜盘及缸体- 配流盘组成的摩擦副直接参与高压油液的输送过程,被视为3大关键摩擦副。围绕3大关键摩擦副的动力学分析及热流固耦合润滑特性分析是过去研究者广泛关注的重点,已取得丰硕的研究成果,对工程设计产生了显著的促进作用[3-5]。然而,对于未直接参与输送油液过程的回程盘- 中心球铰摩擦副(以下简称回程球铰副),长期以来被视为辅助摩擦副部件,目前只有在教科书与产品手册中附带提及,鲜见深入的分析与讨论。近年来,随着对静液驱动系统的功率密度和可靠性要求不断提升,发现回程球铰副在服役过程中因润滑不良而产生不同程度的非预期磨损与烧蚀等故障,严重危害轴向柱塞泵的工作稳定性与可靠性[6]。因此,有必要对回程球铰副的润滑机理开展深入研究。
球面滑动摩擦副以关节轴承为应用背景积累了相对丰富的研究成果。文献[7-8]指出磨损失效与强度失效是关节轴承的主要失效形式,这两类失效形式均与摩擦副的配合关系有直接关系。目前球面滑动摩擦副配合关系的设计理论尚不成体系,一般依靠经验数据选用配合关系,这严重制约了关节轴承最佳性能的实现与使用寿命的提高。文献[9]利用商业有限元软件对关节轴承的间隙进行了优化设计研究,结合实验结果证明优化后的磨损寿命得到显著提高。由于利用商业有限元软件分析关节轴承的计算成本较高,文献[10]提出了计算关节轴承静态接触应力分布的半解析计算方法,其计算结果得到了文献[11]的实验结果验证。无论是有限元方法还是半解析算法,现有关节轴承的计算方法均未考虑固体表面相对运动的影响,故无法考虑润滑介质的压力支撑效果。
在摩擦副间隙内油膜润滑机理研究方面,JFO理论是描述油液润滑成膜机理的最前沿学说之一。JFO空化算法起源于Jakobsson等[12]研究有限宽度径向滑动轴承油膜压力分布问题,后经过Olsson[13]在数学上进行简化改进,形成了当今摩擦学领域公认的、与实验结果吻合最好的润滑力学计算方法之一。尽管JFO空化算法成功解决了径向滑动轴承、推力轴承及机械密封等平面摩擦副的润滑机理分析问题,但鲜有报道其在球面滑动摩擦副润滑机理分析中的应用。
球面滑动摩擦副是具有复杂相对运动规律、摩擦学设计难度大、加工精度要求高及尖端市场需求广泛的关键零部件。本文以轴向柱塞泵用回程球铰副作为研究对象,利用其几何结构特征,开展运动学分析,改进并应用JFO空化数值算法,研究摩擦副油膜压力形成机理,掌握稳态条件下特征参数之间的内在联系,为相关工程设计提供基础理论支撑。
1 数学模型建立
1.1 运动学分析
斜盘型轴向柱塞变量泵(以下简称柱塞泵)是通过调整柱塞行程实现变量输送高压油液的机械元件。图1展示了柱塞泵的基本结构,柱塞位于缸体内均布的柱塞腔中,柱塞头部装有滑靴,由于回程机构(回程盘、中心球铰、压紧弹簧)的作用,迫使滑靴底部始终贴紧于斜盘的表面滑动,斜盘相对缸体端面的倾斜角度决定了柱塞的有效行程。随着泵轴不断地旋转,柱塞在柱塞腔内往复运动,连续不断地吸油和压油,改变斜盘倾角即可改变柱塞泵的排量。
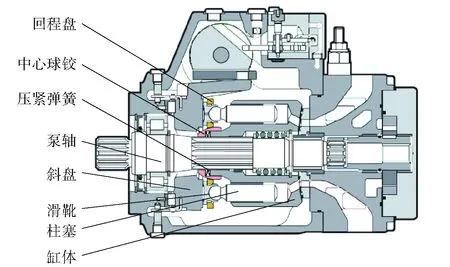
图1 力士乐A4VG系列柱塞泵的基本结构[14]Fig.1 Schematic diagram of internal structure of Rexroth A4VG series pump[14]
由于相对运动行为复杂多变且高精度球面加工难度大,回程球铰副是回程机构的易损部分。回程球铰副由回程盘与中心球铰配对组成,回程盘在与斜盘表面平行的平面上以斜盘中心轴线为轴作圆周回转运动;中心球铰绕泵轴中心轴线作圆周回转运动。滑靴与回程盘直接接触,各滑靴连续交替推动回程盘,其产生的力学结果是回程盘在平行于斜盘的平面上做匀速圆周运动。中心球铰通过压紧弹簧与缸体相互作用,并通过花键与泵轴相连,故中心球铰的转速与泵轴转速相同。回程盘与中心球铰围绕各自的轴线作圆周运动,回程球铰副的中心就是两条轴线的交点。因此,回程球铰副是一个多自由度的球面滑动摩擦副润滑问题。
为了剖析回程球铰副的运动学特性,如图2所示,对回程球铰副的基本结构建立直角坐标系Oxyz与直角坐标系Ox1y1z1.假设回程盘球窝与中心球铰完全同心,即回程球铰副的几何中心,定义为坐标系的原点O,回程盘的旋转轴线定为x轴,泵轴的中心轴线定为x1轴,平面Oyz平行于斜盘端面,平面Oy1z1平行于缸体端面,z轴与z1轴重合,是斜盘倾斜时围绕的轴线,坐标轴中心球铰的曲率半径为rb. 因此,回程球铰副的运动行为在上述坐标系框架内可描述为:回程盘在平面Oyz上围绕x轴旋转,中心球铰在平面Oy1z1上围绕x1轴旋转,斜盘绕z轴或z1轴倾斜的角度α对应为x1轴与x轴的夹角。
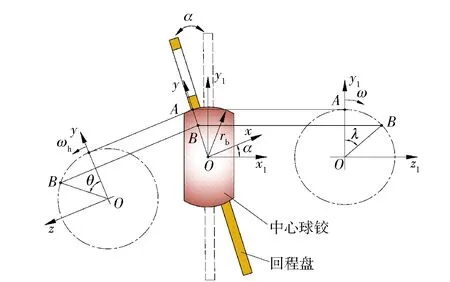
图2 回程球铰副双正交坐标系Fig.2 Double orthogonal coordinates of retaining spherical pair
回程盘是一类薄盘形零件,由于其厚度L远小于中心球铰的球径长度(L/2rb< 0.1),忽略摩擦副沿宽度方向(即x方向)的变化,回程球铰副摩擦副降维简化成具有柱面特征的摩擦副。柱面摩擦副具有两个自由度的相对运动,对应于图2中的Oxyz坐标系,一个自由度是沿x轴方向的相对滑动,一个自由度是围绕x轴旋转的圆周运动。
假设点B代表了回程球铰副接触区内的任意对应位置,y轴和y1轴分别对应为回程盘与中心球铰的转动零点位置。在平面Oyz内回程盘上点B对应位置转过的角度记为θ,在平面Oy1z1内中心球铰上点B对应位置转过的角度记为λ.
在Oxyz坐标系中,点B的位置坐标为
(1)
在Ox1y1z1坐标系中,点B的位置坐标为
(2)
转角λ可表达为
(3)
假设泵轴以恒定角速度ω旋转,λ与ω满足
(4)
式中:t是时间。
对(3)式求导,可得到回程盘的角速度:
(5)
先将中心球铰上点B对应位置的速度矢量投影到直角坐标系Oxyz中:
(6)
式中:vbx、vby、vbz分别是中心球铰上B点速度投影到x、y、z方向上的分量。
再将回程盘上点B对应位置的速度矢量分解到直角坐标系Oxyz中:
(7)
式中:vhx、vhy、vhz分别是回程盘上B点速度投影到x、y、z方向上的分量。
将(6)式与(7)式按照各个方向进行相减运算,得到在直角坐标系Oxyz中相对速度矢量:
即
(8)
联系(3)式与(5)式,对(8)式进行化简,得
(9)
式中:Δvyz是回程球铰副在Oyz平面上的投影分量,其特征为绕x轴的旋转运动。
当柱塞泵稳定运转时,泵轴转速ω和中心球铰半径rb是固定不变的,通过给定不同的斜盘倾角α调整输出排量的大小。因此,在高转速、大排量工况条件下回程球铰副的相对速度Δvx与Δvyz具有最大值。
1.2 润滑机理分析
在充分润滑的状况下,回程球铰副的间隙内充满了以液压油为主的润滑介质,非等厚黏性油膜在剪切运动固体表面的带动下形成压力场,从而将固体表面撑开。根据1.1节的简化假设,在相对滑动速度Δvx方向上,Δvx是与x位置无关;同时根据柱面假设,摩擦副间隙在x方向上是均匀的,因此,在x方向没有形成油膜支撑压力的收敛间隙条件。而在绕x轴相对旋转线速度Δvyz方向上,Δvyz计算式的常数部分是θ的函数,而且回程盘相对中心球铰在Oyz平面内存在一定程度的偏心,偏心造成间隙大小分布不均匀,因此,在圆周方向具有形成动压润滑的基本条件,即回程球铰副在圆周转动方向是形成润滑压力的主要方面。
在平面Oyz内,不妨假设中心球铰的几何中心静止且固定,那么圆周角度θ和回程盘相对中心球铰的偏心率ε,满足:
θ=φ0+φ,
(10)
(11)
式中:φ0偏位角;φ是以最大间隙处为起点的角度;e是偏心距;c是设计间隙值。
由于摩擦副间隙内的油膜厚度约是中心球铰半径长度的103量级,回程球铰副的曲面效应可忽略不计。将油膜沿圆周方向展开,建立直角坐标系Oξψ,如图3所示。

图3 回程球铰副油膜坐标系Fig.3 Cartesian coordinates of oil film in retaining spherical pair
油膜压力场p(ξ,ψ)的控制方程是稳态雷诺方程[15]:
(12)
其边界条件为
(13)
式中:p是油膜压力;p0为环境压力;ρ是油膜密度;μ是油膜黏度;h是油膜厚度分布函数,在充分润滑的假设下等于间隙形状分布,
h=c[1+εcos (θ-φ0)].
(14)
通过(12)式计算得会得到油膜压力p低于空化压力pc的区域,称为空化区。在空化区内,油膜是油气两相混合物,其压力近似为常数,等于空化压力pc;在非空化区内,油膜是纯液相的,其密度近似认为是常数,记为ρc[12-13].
因此,在液膜区内,(12)式化简为
(15)
在空化区内,(12)式化简为
(16)
空化区边界需满足以下条件:在油膜破裂处,
(17)
在油膜重生处,
(18)
式中:n是空化区边界的法向坐标;vn是法向速度。
(15)式~(18)式是JFO空化算法的核心,其中心思想是在油膜内部的空化过程中流量保持连续。
沿y方向,对油膜压力场p(ξ,ψ)积分得到油膜承载力Fp,其表达式为
(19)
2 数值算法
2.1 无量纲化
针对油膜压力场计算所涉及的JFO空化算法,前人提出了多种数值求解方法,本文采用文献[16]提出的有限体积方法进行求解。(15)式~(18)式是JFO空化算法的核心表达式,为了统一数学表达式与简化计算流程,在此引入空化指数F和通用变量Φ:
(20)
(21)
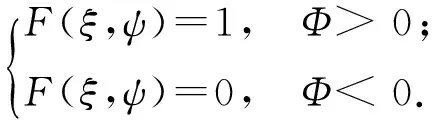
(22)
以上表明,Φ是一个兼有两重含义的无量纲物理量:当F= 1时,此时Φ是液膜区的无量纲压力;当F= 0时,此时Φ是空化区的无量纲密度。
将以上无量纲变量与(20)式~(22)式代入稳态雷诺方程(12)式,得到
(23)
对(23)式进行数值计算,通过循环迭代不断调整空化指数F与通用变量Φ的值,就可获得空化区的实际范围,从而将(17)式和(18)式自动纳入计算程序,避免了因反复搜索空化区边界位置而产生的计算量。
2.2 算法流程
图4给出了回程球铰副油膜润滑数值模型的计算流程,其中包含3次循环迭代:1)根据通用变量分布Φ(X,Y)的正负特征更新空化指数分布F(X,Y),迭代求解压力分布p(X,Y);2)通过比较偏位角大小,迭代求解偏位角φ0;3)采用二分法修正偏心率ε,迭代求解平衡条件下的油膜承载力Fp.
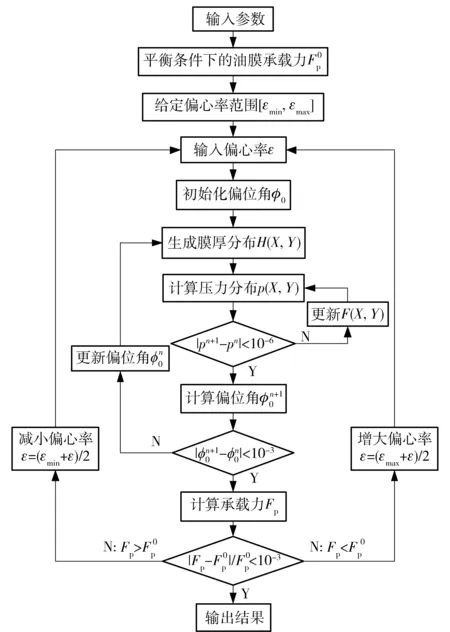
图4 回程球铰副润滑数值分析流程Fig.4 Flow chart of numerical analysis of lubrication in retaining spherical pair
在第1循环迭代过程中,根据偏心率ε与偏位角φ0的值,生成场变量如膜厚分布H(X,Y)等;基于有限体积法对方程(23)式进行离散化处理,求解域用20×20的均匀网格进行剖分,利用高斯赛德尔法求解离散方程组,得到通用变量分布Φ(X,Y);根据通用变量分布的正负更新空化指数分布F(X,Y);如果前有两次迭代得到的压力分布相差小于预先设定的收敛判据10-6,则该循环结束。
在第2循环迭代过程中,根据已得到的压力分布p(X,Y),计算偏位角φ0,比较前后两次迭代得到的偏位角大小,如果相差小于预先设定的收敛判据10-3,则该循环结束。
经过3次循环迭代,可获得受力平衡条件下的计算结果,经过量纲恢复环节,输出剪切速度分布Δvyz(ξ,ψ)、油膜厚度分布h(ξ,ψ)、油膜压力分布p(ξ,ψ)、空化指数分布F(ξ,ψ)等计算结果。
2.3 算法验证
选取径向滑动轴承为验证本文算法的对象。围绕径向滑动轴承,前人展开了深入的实验测试研究,文献[12]提供了沿圆周方向的压力分布测量结果,如图5中散点“o”所示。实验结果显示,沿圆周方向,压力先升高至峰值,后迅速下降至空化压力,空化区内压力分布曲线平坦,最后压力回升、回归至周向起点处的压力值。图5中表明本文算法获得的计算结果,与文献[12]的实验结果在总体趋势上表现一致,除了在峰值压力附近,本文计算结果略大于实验结果,其余部分二者几乎完全吻合。综上,本文算法得到了实验结果的验证。
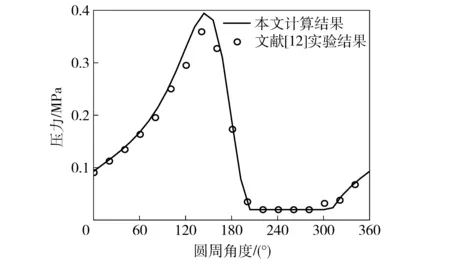
图5 数值算法验证Fig.5 Verification of numerical algorithm
3 计算结果与分析
3.1 算例设置
表1展示了3种典型斜盘倾角工况的算例,即7.5°、12.5°与17.5°,其余几何与工况参数保持相同,以此来分析油膜参数分布特征,揭示回程球铰副油膜润滑压力形成机理。
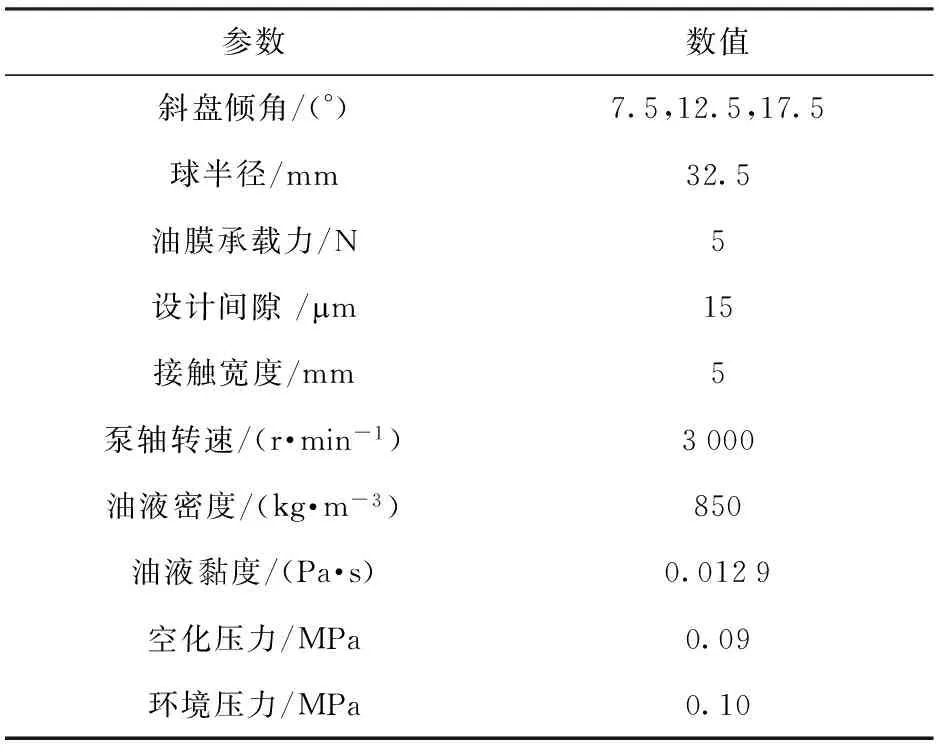
表1 算例参数Tab.1 Calculating parameters
3.2 计算结果
图6展示了3种斜盘倾角条件下回程球铰副间隙内的油膜压力分布情况。对比3种斜盘倾角条件下的压力分布,发现压力分布沿圆周方向分布特征类似:先降低到第1低谷压力后升高到第1峰值压力,再降低到第2低谷压力后升高到第2峰值压力,第1峰值压力明显大于第2峰值压力,两次低谷压力值近似相等。在倾角为7.5°条件下,低谷压力接近空化压力,最大低谷压力出现在第2低谷压力区,第2低谷压力覆盖的范围也大于第1低谷压力覆盖的范围。在倾角为12.5°和17.5°的两种条件下,低谷压力为空化压力。低谷压力范围随着倾角增大而增大,而第1峰值压力范围与第2峰值压力范围均随着倾角增大而减小,但第1峰值压力与第2峰值压力对应的最大压力值随着倾角的增大而增大,以上现象表明增加斜盘倾角具有“推挤压力”的作用,加大了油膜压力的两极分化趋势。
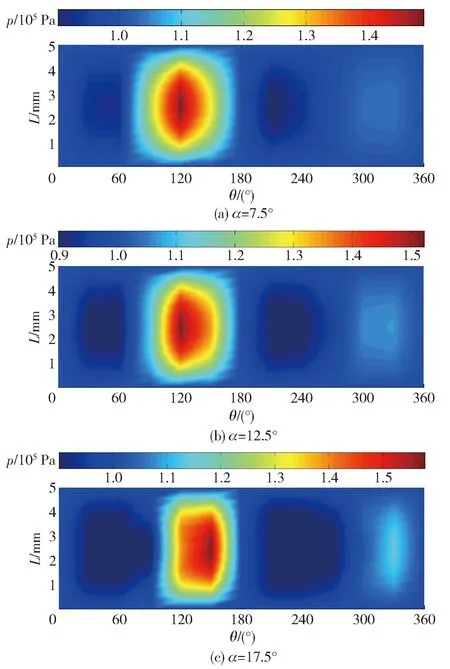
图6 在不同的斜盘倾角条件下的压力分布Fig.6 Pressure distribution at different tilting angles of swash plate
图7展示了与图6对应的3种斜盘倾角条件下回程球铰副间隙内的空化指数分布情况。空化指数反映了空化区的分布范围,空化指数为1代表没有空化,空化指数为0代表发生空化。对比3种斜盘倾角条件下的空化指数分布,发现空化指数分布范围随着斜盘倾角增加而增加:在斜盘倾角为7.5°条件下,全场空化指数为1,表明不存在空化现象;在斜盘倾角为12.5°条件下,全场出现两片空化指数为0的区域,沿圆周方向一小一大,对应于压力分布的低谷压力覆盖范围内;在斜盘倾角为17.5°条件下,全场出现两片空化指数为0的区域,沿圆周方向一小一大,对应于压力分布的低谷压力范围内,较斜盘倾角12.5°条件的计算结果,两片空化区的面积均明显增大,但对应位置大致相当。综合以上讨论结果,增加斜盘倾角催生并加剧了空化现象,造成油膜破裂严重化。
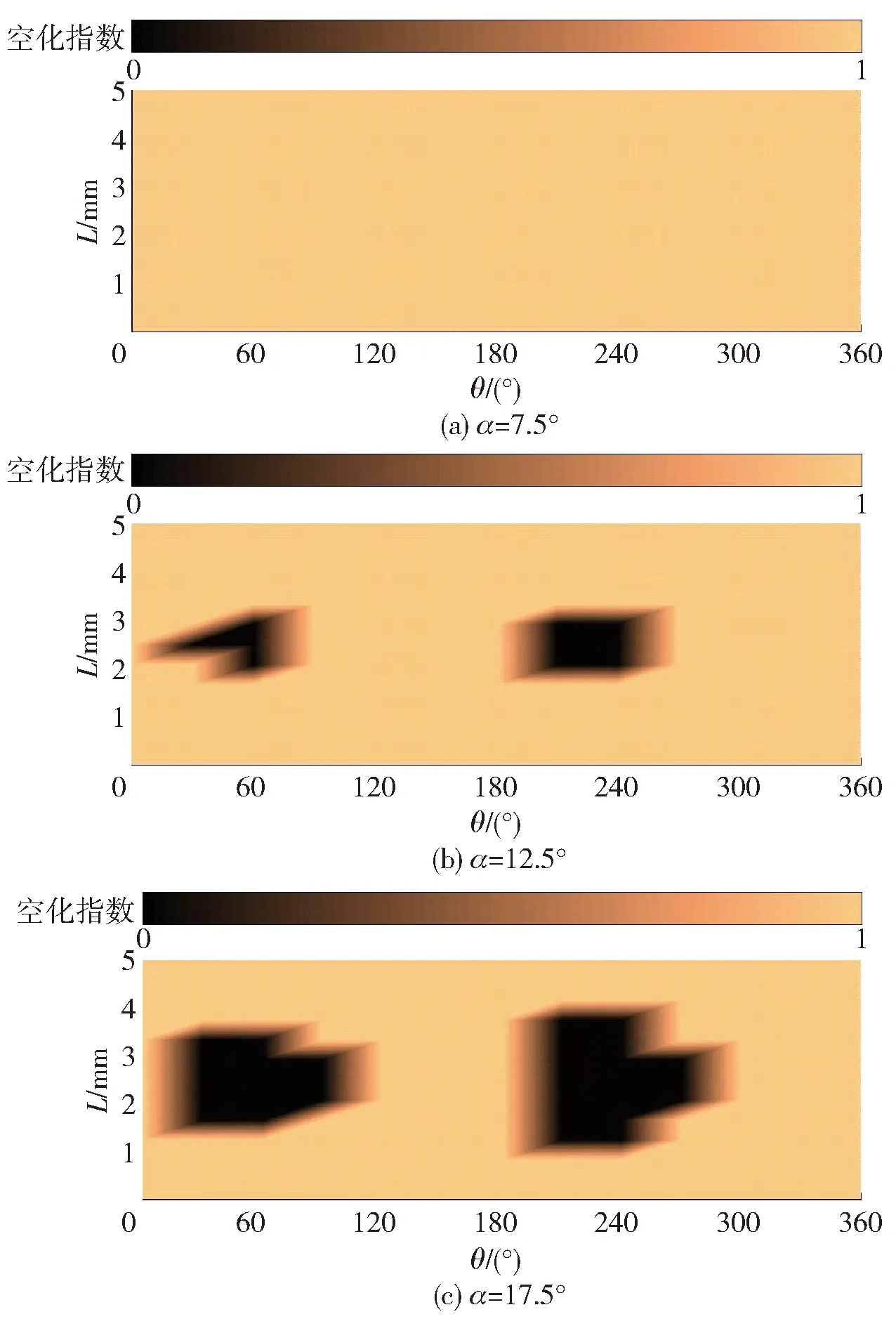
图7 在不同的斜盘倾角条件下的空化指数分布Fig.7 Distribution of cavitation index at different tilting angles of swash plate
3.3 油膜压力形成机理分析
图8展示了在斜盘倾角17.5°条件下ψ=L/2截面处的剪切速度分布、油膜厚度分布、空化指数分布及压力分布,θ从0°变化到360°对应为油液速度流动方向。固体表面剪切运动带动油液发生相应的剪切速度流动,在圆周方向上,表面剪切速度出现2个周期的正弦波动变化,间隙形状出现1个周期的间谐波动变化。因流量连续,油液从大口流入小口造成压力升高,反之压力降低的现象,被称为“动压效应”;同样的,因流量连续,表面剪切速度随位置增加造成压力降低,反之压力升高的现象,被称为“伸缩效应”。回程球铰副间隙内的压力分布就是伸缩效应与动压效应复合叠加的结果。在θ为0°至134°阶段,摩擦副间隙逐渐变小,动压效应造成压力升高,表面剪切速度先增加后减小,伸缩效应造成压力先降低后升高,在整个过程中,伸缩效应较动压效应更剧烈,故压力先降低形成第1空化区,后迅速升高形成第1高压区,在最小间隙处,油膜压力达到最大值。在θ为134°至324°阶段,摩擦副间隙逐渐变大,动压效应造成压力降低,表面剪切速度先减小后增加再减小,伸缩效应造成压力先升高后降低再升高,首尾两段的伸缩效应较动压效应明显微弱,故形成第2空化区。在θ为324°至360°阶段,摩擦副间隙逐渐减小,动压效应造成压力升高,表面剪切速度大幅减小,伸缩效应造成压力升高,故压力升高形成第2峰值压力区。对比第1空化区与第2空化区的覆盖范围,发现第2空化区较大,这是因为伸缩效应与动压效应负向叠加共同造成压力降低;对比第1峰值区与第2峰值区,第1峰值区达到的压力较高,这是因为伸缩效应与动压效应正向叠加共同造成压力升高。结合传统的径向滑动轴承计算结果(见图5),由于没有伸缩效应的影响,故在间隙减小阶段压力升高曲线光滑饱满,具有良好的承载能力。回程球铰副的计算结果显示,受到伸缩效应的影响,压力升高过程被打断,压力降低过程被拉长,总体承载能力被大幅削弱。因此,在摩擦副设计过程中,应考虑回程球铰副相对速度分布造成的承载能力被削弱的因素,从而为改善油膜承载特性的角度提出相应的设计方案。
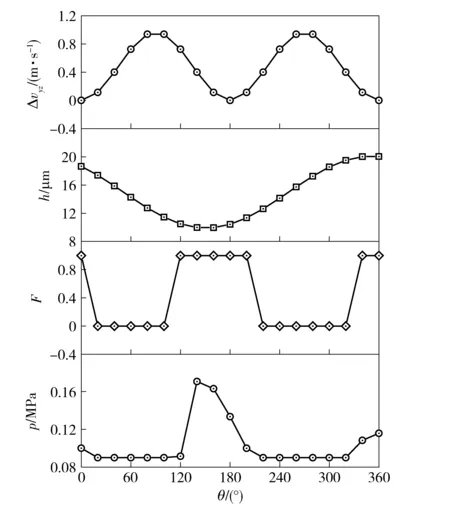
图8 在ψ =L/2截面处的油膜润滑压力形成机理Fig.8 Mechanism of pressure forming along the circumferential direction for ψ =L/2
4 结论
在轴向柱塞泵中,回程球铰副是回程盘与中心球铰组成的机械结构,存在复杂的空间相对运动关系。结合回程球铰副几何特征,提出了基于柱面特征的润滑机理分析模型。考虑复杂表面剪切速度影响因素,拓展JFO空化算法,建立了回程球铰副油膜润滑数值计算方法,并经过经典径向滑动轴承实验结果的验证。针对3种斜盘倾角工况对比分析润滑状态,获得如下结论:
1) 回程球铰副内的油膜压力分布是伸缩效应与动压效应综合作用的结果。
2) 斜盘倾角增大,回程球铰副表面剪切速度升高,强化了伸缩效应对油膜润滑状态的影响。
3) 伸缩效应打断了动压效应引起的连续升压趋势,又扩大了空化低压区的覆盖范围,成为润滑承载力降低的重要方面。
通过上述研究,揭示了回程球铰副的润滑压力形成机理,有助于相关摩擦学设计的展开,为斜盘型轴向柱塞变量泵优化设计与实验研究提供了参考。
References)
[1] 李壮云. 液压元件与系统[M]. 第3版. 北京:机械工业出版社, 2014:68-73. LI Zhuang-yun. Hydraulic elements and system [M]. 3rd ed. Beijing: Mechanical Industry Press, 2014. (in Chinese)
[2] 王意. 车辆与行走机械的静液压驱动[M]. 北京:化学工业出版社, 2014. WANG Yi. Hydrostatic transmissions for vehicle and mobile machinery[M]. Beijing: Chemical Industry Press, 2014. (in Chinese)
[3] 林硕, 苑士华, 刘洪. 考虑油膜非均匀性的滑靴润滑特性研究[J]. 北京理工大学学报, 2014, 34(4): 358-362. LIN Shuo, YUAN Shi-hua, LIU Hong. Analysis on lubrication characteristics of slipper bearing considering un-uniform gap[J]. Transactions of Beijing Institute of Technology, 2014, 34(4): 358-362.(in Chinese)
[4] 王智慧, 苑士华, 彭增雄. 柱塞副油膜温度分布的数值分析[J]. 汽车工程, 2013, 35(9): 781-784. WANG Zhi-hui, YUAN Shi-hua, PENG Zeng-xiong. Numerical analysis on the temperature distribution of oil-film in plunger pair[J]. Automotive Engineering, 2013, 35(9): 781-784. (in Chinese)
[5] Pelosi M, Ivantysynova M. The impact of axial piston machines mechanical parts constraint conditions on the thermo-elastohydrodynamic lubrication analysis of the fluid film interfaces[J]. International Journal of Fluid Power, 2013, 14(3): 35-51.
[6] 张静, 胡亮, 李小军, 等. 基于虚拟样机技术的轴向柱塞泵回程盘动力学特性仿真分析[J]. 液压与气动, 2016(3): 86-91. ZHANG Jing, HU Liang, LI Xiao-jun, et al. The dynamic characteristic simulation of retainer plate in axial piston pump based on virtual prototype technology[J]. Chinese Hydraulics & Pneumatics, 2016(3): 86-91.(in Chinese)
[7] 曲庆文, 刘源勇, 钟振远, 等. 关节轴承的设计特点及分析[J]. 润滑与密封, 2004, 164(4): 102-105. QU Qing-wen, LIU Yuan-yong, ZHONG Zhen-yuan, et al. Design characteristic and analysis for the spherical plain bearing[J]. Lubrication Engineering, 2004, 164(4): 102-105.(in Chinese)
[8] 牛劲草. 向心关节轴承应力场分析及寿命预测方法研究[D]. 洛阳:河南科技大学,2013 NIU Jin-cao. Study on the three-dimensional stress fields and wear-life estimation method for spherical plain bearings[D]. Luoyang: Henan University of Science and Technology, 2013.(in Chinese)
[9] 向定汉,王春艳,董伟峰. 向心关节轴承的结构优化及摩擦磨损性能研究[J]. 摩擦学学报, 2004, 24(6): 564-567. XIANG Ding-hai, WANG Chun-yan, DONG Wei-feng. Structural optimization and friction and wear behavior of a radial spherical plain bearing[J]. Tribology, 2004, 24(6): 564-567.(in Chinese)
[10] Fang X, Zhang C, Chen X, et al. Newly developed theoretical solution and numerical model for conformal contact pressure distribution and free-edge effect in spherical plain bearings[J]. Tribology International, 2015, 84: 48-60.
[11] Germaneau A, Peyruseigt F, Mistou S, et al. Verification of a spherical plain bearing finite-element model using scattered light photoelasticitytests[J]. Proceedings of Institution Mechanical Engineers Part J: Journal of Engineering Tribology, 2008, 222(5): 647-656.
[12] Jakobsson B O, Floberg L. The finite journal bearing considering vaporization[D]. Goteborg, Sweden: Chalmers University of Technology, 1957.
[13] Olsson K O. Cavitation in dynamically loaded journal bearings[D]. Goteborg, Sweden: Chalmers University of Technology, 1964.
[14] Bosch Rexroth AG Hydraulics Axial Piston Units. A4VG series 32 operating instructions: RE920003-01-B/04.08 [Z/OL]. Germany: Bosch Rexroth Group, 2008. http:∥www.boschrexroth.com/brm.
[15] 温诗铸, 黄平. 摩擦学原理[M]. 第4版. 北京: 清华大学出版社, 2012. WEN Shi-zhu, HUANG Ping. Principles of tribology [M]. 4th ed. Beijing: Tsinghua University Press, 2012. (in Chinese)
[16] Payvar P, Salant R F. A computational method for cavitation in a wavy mechanical seal[J]. Journal of Tribology, 1992, 114(1): 199-204.
Research on Lubrication Mechanism of Retaining Spherical Pair of Variable Displacement Axial Piston Pump
WANG Tao1,2, MAO Ming1,2, TANG Shou-sheng1, GAI Jiang-tao1,2, JI Hai1
(1.Science and Technology on Vehicle Transmission Laboratory, China North Vehicle Research Institute, Beijing 100072, China;2.Collaborative Innovation Center of Electric Vehicles in Beijing, Beijing Institute of Technology, Beijing 100081, China)
Retaining spherical pair is widely used in variable displacement axial piston pump with the feature of complex spatial relative motions. According to the kinematic relation and geometric feature of retaining spherical pair, a physical model based on the cylinder feature is proposed to study the process of oil lubrication between ball guide and retaining plate. And the lubricating film within retaining spherical pair is numerically investigated based on the modified Jakobsson-Floberg-Olsson (JFO) cavitation algorithm to consider the influence of shearing velocity. The relations among the distributions of shearing velocity, clearance shape, cavitation index and pressure under the conditions of three different tilting angles of swash plate are discussed. The research results show that the pressure distribution has the characteristics of double peak and double valley, which is depended on the hydrodynamic effect resulted from the clearance shape and the hydrostrictive effect due to shearing velocity. The hydrostrictive effect is positively correlated with the tilting angle of swash plate which plays an important role in eliminating the amount of load support.
ordnance science and technology; axial piston pump; retaining spherical pair; dynamic lubrication; JFO cavitation algorithm; film cavitation
2016-05-10
国家自然科学基金青年科学基金项目(51605450)
王涛 (1986—),男,副研究员,博士。E-mail: tonywangbj@aliyun.com
TH137.51
A
1000-1093(2017)03-0424-09
10.3969/j.issn.1000-1093.2017.03.002
