不同浪向下大型回转式起重船回转起吊作业过程的动力学分析❋

张大朋， 朱克强

(宁波大学海运学院，浙江 宁波 315211)

不同浪向下大型回转式起重船回转起吊作业过程的动力学分析❋

张大朋， 朱克强❋❋

(宁波大学海运学院，浙江 宁波 315211)

随着海洋开发从浅水走向深水，各种特种船舶在海洋工程建设中发挥的作用日益重要。起重船是海洋工程建设的重要工程船舶，是海洋开发的必备工具。为了更好的开发利用海洋资源，有必要进行相关设备的研究。参考某回转式起重船的具体参数，结合该船工作时的具体过程，利用大型水动力分析软件OrcaFlex建立了该起重船回转起吊作业状态下的动力学分析简化模型。通过调节不同海况下的浪向，实现了对大型回转式起重船回转起吊作业过程的的动力学分析，得到了吊物就位时不同浪向下的与接收船甲板的碰撞力、吊缆张力等，对比并分析了不同浪向时吊缆的张力变化，确定了吊物的最小碰撞力和吊缆的张力大小及波浪方向，结合计算结果，给出了大型回转式起重船回转起吊作业的优化设计方案。

回转式起重船； OrcaFlex； 动力学分析； 碰撞力； 吊缆张力

起重船是海洋工程建设的重要工程船舶，是海洋开发的必备工具。为了更好的开发利用海洋资源，有必要进行相关设备的研究。周国宝、米旭峰[1]等对起重船的扒杆结构强度进行了有限元分析，对构建的应力进行了计算并与规范进行了比较；董达善、孙友刚等[2]对海上浮吊的补给作业进行了仿真研究，结果表明绳长、下降速度对起吊作业有重要影响；董艳秋、韩光[3]对起重吊物系统波浪中的动力学响应进行了分析，建立了起吊过程中重物运动的非线性微分方程组；顾永宁、胡志强等[4]对大型起重船波浪诱导下吊索的附加动力载荷进行了研究，对海上作业进行了定性和定量分析；R. G. Lueck等[5]对垂直吊放系统运用小波变换进行了时域响应预报。从相关文献来看，对在某一特定浪向下起吊作业动力学响应的研究较多，但对于不同浪向下起吊系统的动力学响应的研究较少。而浪向的改变对于起吊作业有重要影响。本文通过时域耦合动力分析方法分析回转式起重船系统的非线性动力学特性。结合水动力性能的计算结果给出了一些指导性的建议，对于保证海上安全作业有重要意义。

1 海洋环境载荷的计算理论

1.1 波浪理论的选择

Dean[6]指出在各种水深线性波浪理论都可以给出不错的结果，且随着水深的增加海浪基本控制方程中的非线性项的影响逐渐降低，因此本文在OrcaFlex的建模过程中选用线性波浪理论。

1.2 船体RAO

RAO，即Response Amplitude Operator，可以用来计算船舶在海中工作时的行为。船体RAO一般可以通过船舶的水池模型实验来获得。其本质是一个由波浪激励到船体运动的传递函数，在OrcaFlex中，一旦船体的RAO确定，那么波浪所引起船体的运动就将是确定的。船体运动响应特性可以用船体响应幅频因子(RAO)进行描述。一阶波浪力所引起的船体偏移用响应幅频因子(RAO)进行定义，如下：

x=R·a·cos(ωt-φ)，

(1)

其中：x是浮体位移响应(升沉、纵荡、横荡是长度单位，艏摇、横摇、纵摇是角度单位)；a,ω是波浪的振幅和频率；R是RAO 响应的系数；φ是相位；RAO的坐标原点取在船体的设计水线处。

1.3 风流作用在船体上的力和力矩的计算

在OrcaFlex中给出的风和流力的计算方式是根据特定的模型试验得到的无量纲系数结合OCIMF给出的公式来确定的。

风作用于船上的力和力矩可以用以下几组公式计算：

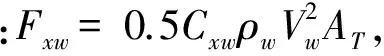
(2)

横向力：Fyw= 0.5CywρwVw2AL,

(3)

(4)

流作用于船上的力和力矩可以用以下几组公式计算：

纵向力：Fxc= 0.5CxcρcVc2TLBP,

(5)

横向力：Fyc= 0.5CycρcVc2TLBP,

(6)

(7)

其中：Cxw是无量纲纵向风力系数；Cyw是无量纲横向风力系数；Cxyw是无量纲风的摇摆力矩系数；ρw是20°C时空气的密度，取1.223kg/m3；Vw是10m高处的平均风速，kn；AT是船体水面上的横向受风面积，m2；AL是船体水面上的纵向受风面积；LBP是船舶的两柱间长；Fxw是风作用于船上的纵向力，kN；Fyw是风作用于船体上的横向力，kN；Mxyw是风作用于船体上的横摇力矩，kN·m；Cxc是无量纲纵向流体系数；Cyc是无量纲横向流力系数；Cxyc是无量纲流的摇摆力矩系数；ρc是20°C时海水的密度，取1025g/m3；是平均流速，kn；T是船舶吃水，m；Fxc是流作用于船体上的纵向力，kN；Fyc是流作用于船体上的横向力，kN；Mxyc是流体作用于船体上的摇摆力矩，kN·m。

1.4 吊缆张力的计算

吊缆的性能相当于一个非线性弹簧[7]，离散为凝集质量模型[8]，由若干个连续的、无质量分段和处于各分段中点处的节点组成，将其模拟为轴向、旋转弹簧和阻尼器的组合体。节点集中了两个相邻分段各一半的质量，力和力矩都作用于节点上，这也正是OrcaFlex中对吊缆张力建立模型的数学基础[9-13]。

在OrcaFlex中对吊缆有效张力的计算：

Te=Tw+PoAo-PiAi,

(8)

(9)

式中:Te表示有效张力；Po表示外部压力；Ao表示缆索横截面积；Tw表示壁面张力；EA是缆轴向刚度；ε=(L-λL0)/λL0是总的轴向平均应变；λ是分段伸长系数；L0是分段原长；v是泊松比；Pi,Po分别为内、外部压力；Ai,Ao分别为缆绳内、外部的横截面面积，对于缆索而言，其内部横截面积为0；e为缆索阻尼系数，一般忽略不计，在本文中e取为0；dL/dt是长度增加的速率。

1.5 起重物与接收船甲板接触碰撞力的计算

对于碰撞力的计算国内外相关的应用成果基本上采用的是动能公式的形式[14]，但在OrcaFlex中却并不是这样算。在OrcaFlex中，船体本身是一个无法变形的刚体。要计算船舶的碰撞力，需要在船体表面加一层弹塑性固体，进而建立接收船船与起重物碰撞的弹塑性变形动力分析模型，根据弹塑性固体的变形量计算出接收船舶甲板与起重物的碰撞力。弹塑性固体发生变形时的碰撞力为：

FP=KAPd,

(10)

其中：K为弹塑性材料的法向材料刚度，kN·m·m-2；Ap为碰撞时接触面积，m2；d为发生碰撞时在垂直弹塑性固体表面方向的变形深度(也叫法向穿透深度)，m。在本算例中材料的法向材料刚度取为10 000 kN·m·m2。

2 在OrcaFlex中回转式起重船回转起吊作业时系统动力学模型的建立

2.1 坐标系、风浪流关系的确定

OrcaFlex用一个全局坐标系G-XYZ来确定坐标轴，G其中代表全局坐标系的起点，GX、GY、GZ分别表示X轴、Y轴及Z轴。对于不同的物块模型，也有相对应的局部坐标系。风浪流相对于x轴和y轴的方向是相对全局坐标系中的GX轴和GY轴而言的，具体如图1、2所示。

图1 全局及局部坐标

2.2 OrcaFlex中船体主尺度的确定

根据实际船体主尺度在OrcaFlex软件中建的模型中船长为103m，型宽为16m，型深为13.32m。设计吃水为6.66m，横稳性半径1.84m，纵稳性半径114m，排水量8 800t，水面上正面投影191m2，水面上侧面投影927m2。方形系数CB为0.804，首摇转动惯性矩为5.83×109kg·m2。本船的RAO、波浪漂移QTFs、附加质量系数及阻尼系数的数据均来自一个103m长的实船在400m水深水池的NMIWave衍射分析。

图2 风浪流方向示意图

2.3 OrcaFlex中模型的建立

在orcaFlex中用起绞盘作用的winch单元和6D浮标进行组合，模拟回转起重船的回转基座，用6D浮标模拟起重吊臂。其中winch单元的作用是牵引6D浮标模拟的基座，使它可以发生旋转。6D浮标模拟的起重吊臂长度为90m，质量为30t。吊臂和基座之间用4根弯曲刚度和扭转刚度极大的line单元固结在一起，以保证吊臂随着基座的转动而转动。起重物垂直方向的下放通过在吊缆下端连接winch单元实现。winch单元的具体原理如图3所示。吊缆的轴向刚度EA为101 000kN，泊松比υ为0.5，长度为57m，外径d为0.04m，内径为0。起重物用6D浮标模拟，质量为60t，几何外形为边长6m的正方体，转动惯Ix=Iy=Iz=100t·m2。为尽量保证模拟的真实程度，用4个起弹簧阻尼器作用的link单元将6D浮标模拟的起重物与3D浮标模拟的缆扣相连，因为在OrcaFlex中link的作用相当于一个弹簧阻尼器，既可以轴向伸缩又可以轴向伸张，这样可以缓冲重物在模拟过程中的冲击，以保证系统整体的运动性能，link原理具体如图4所示。然后再通过缆扣与吊缆下端的winch相连。模型建成后，如图5所示。

图3 Winch作用示意图

图4 link作用示意图

图5 回转作业状态下模型示意图

3 计算结果

设计中主要考虑如下特征海况条件作为设计边界条件：水深为100m，浪向取为0°～180°，每隔15°取一个浪向；波高为2.5m，周期为8s。

3.1 不同浪向时起重甲板承受的支撑力变化

观察图6发现，在大多数浪向下，起重船甲板在起重物被吊起的瞬间由于忽然受到一个瞬时的冲击载荷，使得此时起重船甲板的承受的支撑力瞬时增大到一个极大的值，随着时间的推移，起重船甲板的支撑力逐渐减小，直至起重物被放到接收船上(45°、60°、120°、135°浪向除外)，此时的起重船甲板支撑力稳定在124.92kN，此时甲板的支撑力大体上与起重臂和基座的总重力数值相等。且最大的支撑力发生在浪向为90°时，此时最大支撑力约为1 200kN。而在浪向分别为45°、60°、120°、135°时，经模拟发现，此时起重物已经不能落在接收船上，或是落在接收船上的时间很短而又再次被吊起脱离接收船，此时的起重物会发生绕起吊缆上端点不规则的回转摆动现象，表现在图6中，就是在图中再次在某一不定时刻出现了起重船甲板再次受到了瞬时的冲击载荷，支撑力的瞬间无规律性的增大，但此时瞬间增大的支撑力远小于起重物在起重船上刚刚被吊起时甲板所承受的支撑力。且最大支撑力发生在浪向为90°时，分析产生这种现象的原因为当浪向为90°时，使得船体发生相对其他浪向而言较剧烈的横摇和升沉，而基座与甲板固结，在船体发生以上运动时，为了限制基座发生移动，甲板给予基座的支撑力也会在同时增大。

图6 起重船甲板支撑力随浪向变化图像

3.2 不同浪向时吊重块与接收船甲板的碰撞力变化

观察图7发现，在大约37 s以前，起重物没有与接收船甲板接触，此时的碰撞力为0。同时发现，不同的浪向下，起重物与接收船甲板接触的时间并不相同，但差别不大，基本都在50 s左右已与甲板发生接触。在接触的瞬间，接收船甲板受到冲击载荷的作用，碰撞力瞬时增大后减小，然后随着时间的推移，碰撞力发生不规则性的增大减小的循环性变化。而在浪向分别为45°、60°、120°、135°时，经模拟发现，此时起重物已经不能落在接收船上，或是落在接收船上的时间很短而又再次被吊起脱离接收船，故而在此时接收船的碰撞力经过一段时间后最终又变为0。且吊重物与接收船甲板的最大碰撞力也发生在浪向为90°时，此时的最大碰撞力为1 600kN。分析产生这种现象的原因为当浪向为90°时，使得船体发生相对其他浪向而言较剧烈的横摇和升沉，进而使得起重物与甲板发生较频繁和剧烈的撞击，使得碰撞力大大增大。

图7 接收船碰撞力随浪向变化图像

3.3 不同浪向时吊缆的动力学响应

图8～13为吊缆的动力响应。图8说明在起重物未被吊放到接收船的一段时间内，吊缆张力在受到冲击载荷的情况下瞬时增大到一个极大值(浪向不同，这个值的大小也有所不同)，然后开始发生不规则性的增大减小的循环性变化，在重物与接收船接触后，吊缆张力会急剧减小，但随着起重船的随波逐流现象仍然会发生小幅度的不规则性的增大减小的循环性变化。图9、11说明，浪向不同时，吊缆发生最大弯曲的位置亦不完全相同，但都发生在距离吊缆顶端50～55m之间，且无论何种浪向，在吊缆的顶端和底端的曲率都为0。而图10说明，无论在何种浪向下，吊缆的任何一位置都有被拉直的一瞬间。图12说明沿吊缆长度方向，吊缆的最大张力顶端最大，尾端最小，且沿缆长方向近似呈线性降低，但降低幅度并不剧烈；并非无浪时吊缆顶端的张力最小，而是在在浪向为15°时吊缆顶端的张力最小，在浪向90°时吊缆顶端的张力最大。在浪向为90°时张力最大的原因为，当浪向为90°时，使得起重船船体发生相对其他浪向而言较剧烈的横摇和升沉，进而带动起重臂发生相同运动，而与吊臂相连的吊缆此时的响应幅度自然比其他浪向时剧烈；而在浪向为15°时，初步分析此时的浪向引起的系统响应在相互作用耦合的情况下对于吊缆的响应起了某种升沉补偿的作用，进而此时的吊缆张力最小。图13说明，沿吊缆长度方向发生循环式往复收缩张紧的部位主要是吊缆顶端0～5m处和吊缆尾端50～57m处，因为在这些部位最小张力有负值出现，也就是在这些位置发生了吊缆沿长度方向的收缩，而其他部位的吊缆都是在不同时刻沿缆长方向呈不同的被拉伸状态。

图8 不同浪向时吊缆顶端张力变化历时图像

图9 沿缆长方向最大曲率变化分布

图10 沿缆长方向最小曲率变化分布

图11 沿缆长方向平均曲率变化分布

图12 沿缆长方向最大张力变化分布

图13 沿缆长方向最小张力变化分布

4 结论

(1)在大多数浪向下，起重船甲板在起重物被吊起的瞬间由于忽然受到一个瞬时的冲击载荷，使得此时起重船甲板的承受的支撑力瞬时增大到一个极大的值，随着时间的推移，起重船甲板的支撑力逐渐减小，直至起重物被放到接收船上，此时的起重船甲板支撑力基本维持在一个稳定值，此时甲板的支撑力大体上与起重臂和基座的总重力数值相等。

(2)经模拟发现，对于本算例中的船体而言，在浪向分别为45°、60°、120°、135°时，此时起重物已经不能落在接收船上，或是落在接收船上的时间很短而又再次被吊起脱离接收船。故而这四种浪向时应尽量避免施工作业或是改变此时船体的相对浪向，以保证作业安全。

(3)无论是起重船甲板的支撑力最大值还是接收船甲板的碰撞力最大值都发生在浪向为90°时。

(4)吊缆张力的最小值并非发生在无浪的情况，对于本算例中的船体而言，而是发生在浪向为15°时，可在此种浪向下进行作业，最大程度的保证施工的安全。

(5)沿吊缆长度方向发生循环式往复收缩张紧的部位主要是吊缆顶端部位和吊缆尾端部位，对于本算例中的船体而言，主要发生在吊缆顶端0～5m处和吊缆尾端50～57m处，这些部位极易发生应力集中和疲劳失效，在实际设计的过程中应注意。

[1] 周国宝, 米旭峰, 渠延模. 1 000 t起重船扒杆结构强度有限元分析[J]. 科学技术与工程, 2009, 9(17): 5252-5255. ZHOU Guobao, MI Xufeng, QU Yankai. Finite element analysis of derrick structure Strength for 1 000 t crane ship[J]. Science Technology and Engineering, 2009, 9(17): 5252-5255.

[2] 董达善, 孙友刚, 刘龙. 浮吊海上补给作业的动态特性仿真分析与研究[J]. 科学技术与工程, 2013, 20(13): 5872-5877. DONG Dashan, SUN Yougang, LIU Long. Simulation studies on dynamic characters of floating cranes[J]. Science Technology and Engineering, 2013, 20(13)： 5872-5877.

[3] 董艳秋, 韩光. 起重船吊物系统在波浪中的动力响应[J]. 中国造船, 1993, 1: 63-71. DONG Yanqiu, HAN Guang. Dynamic response of lifting loading system of crane vessel in waves[J]. Shipbuilding of China, 1993, 1: 63-71.

[4] 顾永宁, 胡志强, 谢彬, 等. 大型起重船波浪诱导吊索附加动力荷载研究[J]. 中国海上油气, 2005, 17(3): 197-202. GU Yongning, HU Zhiqiang, XIE Bin, et al.Study on the additional dynamic load of lifting rope due to wave-induced motion of heavy crane barge[J].China Offshore Oil and Gas, 2005, 17(3): 197-202.

[5] Lueck R G, Driscoll F R, Nahon M. A Wavelet for Predicting the Time-domain Response of Vertically Tethered Systems[J]. Ocean Engineering, 2000, 27: 1441-1543.

[6] Dean R G, Perlin M. Intercomparision of near-bottom kinematics by several wave theories and field and laboratory data [J]. Coastal Engineering, 1986, 9: 399-437.

[7] 朱克强, 郑道昌, 周江华, 刘桂云, 包雄关. 生产驳船多点系泊定位动态响应[J]. 中国航海, 2007, 71(2): 6-9. ZHU Keqiang, ZHENG Daochang, ZHOU Jianghua, et al. Dynamic Response of Multi-point Mooring Positioning System of a Moored Production Barge. [J]. Navigation of China, 2007, 71(2): 6-9.

[8] ZHU Ke-qiang, CAI Ying,YU Chun-ling, et al. Nonlinear Hydrodynamic Response of Marine Cable -Body System Undergoing Random Dynamic Excitation[J]. Journal of Hydrodynamics, 2009, 21(6): 851-855.

[9] ORCAFLEX Help File and User Manual[EB/OL]. www.oricina.com.

[10] 朱克强, 李道根, 李维扬. 海洋缆体系统的统一凝集参数时域分析法 [J]. 海洋工程, 2002, 20(2): 100-104. ZHU Keqaing, LI Daogen, LI Weiyang.Lumped-parameter analysis method for time-domain of ocean cable-body system[J]. The Ocean Engineering, 2002, 20(2): 100-104.

[11] YANG Bing-ka, ZHU Ke-qiang, ZHU Yan-jie, et al. Dynamic response of towed line array [J]. Journal of Hydrodynamics, (Ser B) 2013, 25(4): 616-619.

[12] 朱艳杰, 朱克强, 杨冰卡, 等. 基于凝集质量法的海洋缆索动力学建模与仿真技术 [J]. 海洋工程, 2014, 32(1): 112-116. ZHU Y anjie, ZHU Keqaing, YANG Bingka, et al. Dynamics modeling and emulation technique of the marine cable considering tension and compression bending torsion deformation[J]. The Ocean Engineering, 2014, 32(1): 112-116.

[13] 唐友刚. 海洋工程结构力学 [M]. 天津: 天津大学出版社, 2008: 4-34. TANG Yougang. Structral Dynamics for Offshore Engineering[M].Tianjin: Tianjin University Press, 2008: 4-34.

[14] 周枝荣, 邹颋. 大型油轮系靠泊外海开敞式码头的船舶撞击力计算[J]. 水运工程, 2014, 5(491): 59-63. ZHOU Zhirong, ZOU Ting. Calculation of impact force of large oil tanker berthing at open sea terminal[J]. Port & Waterway Engineering, 2014, 5(491): 59-63.

责任编辑 陈呈超

Dynamic Analysis of Full Circle Swinging Hoisting Operation of Large Revolving Floating Crane Vessel Under Different Wave Directions

ZHANG Da-Peng1， ZHU Ke-Qiang2

(Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China)

With the development of the ocean from shallow water to deep water, the role of various special ships in the construction of marine engineering is becoming increasingly important. The revolving floating crane vessel is an important engineering ship in the construction of ocean engineering, and it is a necessary tool for the development of the ocean. For better development and utilization of marine resources, it is necessary to carry out the research of related equipment. Based on the parameters of a cetain revolving floating crane vessel, combined with the specific process of the floating crane vessel at work, the model of the floating crane vessel under full circle swing hoisting has been established by OrcaFlex. With the change the direction of wave, the dynamic analysis of the system has been made and got the impact force between the support vessel and the hanging object and the tension of the crane wire under different wave directions. At the same time, we got the minimum impact force between the support vessel and the hanging object and the tension of the crane wire and their wave directions.According to the calculated result, the optimization design of the full circle swing hoisting operation of large revolving floating crane vessel has been given.

revolving floating crane vessel; OrcaFlex; dynamic analysis; impact force; tension of the crane wire

国家自然科学基金项目(11272160)资助 Supported by the National Natural Science Foundation of China(11272160)

2014-11-20;

2015-07-03

张大朋(1987-)，男，助研。E-mail:1214265737@qq.com

❋❋ 通讯作者：E-mail: zhukeqiang@nbu.edu.cn

TV131.2

A

1672-5174(2017)05-128-07

10.16441/j.cnki.hdxb.20140379

张大朋，朱克强. 不同浪向下大型回转式起重船回转起吊作业过程的动力学分析[J]. 中国海洋大学学报(自然科学版), 2017, 47(05)：128-134.

ZHANG Da-Peng，ZHU Ke-Qiang. Dynamic analysis of full circle swinging hoisting operation of large revolving floating crane vessel under different wave directions [J]. Periodical of Ocean University of China, 2017, 47(05)： 128-134.