实验教学中围绕重要概念进行问题设计
——以“种群数量的变化”为例*
2017-04-09马会放刘恩山
马会放 刘恩山
(1北京市顺义区第一中学 北京 101300 2北京师范大学生命科学学院 北京 100875)
生物学教学强调对重要概念的理解。探究性实验教学帮助学生在亲历实验过程中形成重要概念,并深入理解、内化科学概念。教师在设计问题时围绕重要概念进行,学生在分析问题、解决问题的过程中,形成对重要概念的理解,促进思维的发展。本文以高中生物学必修3《稳态与环境》模块中“种群数量的变化”一节教学为例,详细说明实验教学中如何围绕重要概念进行问题设计。
1 教学背景分析
1.1教材分析“种群数量的变化”是高中生物学《稳态与环境》模块的教学内容。“探究培养液中酵母菌种群数量的变化”是《普通高中生物课程标准》规定的实验。对于这项探究,教材给学生留出了较大的自主空间,以期培养学生的探究能力。引导学生用数学模型解释生命现象、展示生命活动规律是“种群数量的变化”这节内容教学策略的着眼点。数学模型是用于描述一个系统或其性质的数学形式,是联系实际问题与数学的桥梁,具有解释、判断、预测等重要功能,也是发现问题、解决问题和探索新规律的有效途径之一。学生在构建、分析数学模型的过程中建立生物学概念。
1.2学情分析本实验探究一个真实种群数量变化的规律,这种真实性能很好地调动学生学习的积极性。构建数学模型的方法对于高中学生有一定的难度,教学中通过具体实例让学生领悟,有助于学生对学科重要概念的理解,运用重要概念解决实际问题。
2 本节内容的重要概念和生物学术语
生物学概念之间是有层次关系的,有些概念是本节的重要概念,有些概念是次要概念。生物学术语与生物学概念之间有对应关系。基于对课程标准、教材的分析,归纳本节需要学生理解的生物学概念。
2.1本节涉及的生物学术语数学模型、环境容纳量(K 值)、种群增长的“J”型曲线和“S”型曲线。
2.2重要概念及其结构关系(KC:重要概念,SC:次要概念)
KC1种群数量变化规律可以用数学(公式)模型描述
KC2种群大小受出生率、死亡率、迁入和迁出的影响,并受生物因素和非生物因素的限制
SC2.1在环境适宜、资源充裕的条件下,种群数量以指数形式增长,即种群增长的“J”型曲线
SC2.2在环境和资源有限的条件下,种群数量经过一定时间的增长后趋于稳定,即种群增长的“S”型曲线
SC2.3生态系统能维持种群中的个体数,取决于可利用的生物资源和非生物因素
SC2.4在自然条件下,种群数量趋于稳定后,会在一定的范围内波动。
3 教学目标
1)知识目标:①应用数学模型描述种群数量的变化;②解释种群数量发生变化的原因;③概述种群数量增长的“S”型曲线、“J”型曲线。
2)能力目标:①尝试构建种群数量增长的数学模型,解释种群的数量变动;②使用血球计数板对酵母菌进行计数。
3)情感态度与价值观目标:①认同严谨求实的科学态度在得出科学结论中的重要性;②关注人类活动对种群数量变化的影响。
4 教学重、难点
1)教学重点:尝试构建种群数量增长的数学模型,并据此解释种群数量的变化。
2)教学难点:收集、整理、分析数据;数学模型的应用。
5 实验材料和器械的准备
安琪干酵母、酵母浸粉、蛋白胨、葡萄糖、蒸馏水、7个250 mL锥形瓶(配备封口膜、皮筋)、玻璃棒、1 000 mL烧杯、微量移液器(配备相应的枪头)、摇菌管、酒精灯、镊子、消毒酒精棉、天平、超净台、灭菌锅、摇床、冰箱。
6 实验教学安排(见表1)

表1 种群数量的变化实验教学安排
7 教学过程
7.1回顾实验过程,引入课题教师带着学生回顾实验目的和实验过程:探究一定体积的培养液中,接种少量酵母菌菌种,其种群数量变化的规律。向7瓶体积、成分相同的培养液中,分别接种1 mL菌种;摇床上同时培养,分别培养0 h、2 h、4 h、6 h、8 h、10 h、12 h, 取出放在 4℃冰箱中保存,待课上计数。
7.2归纳推理构建种群增长的“J”型曲线教师以实验室培养的酵母菌为素材,假设酵母菌在理想条件下增长,引导学生归纳推理构建种群增长的数学模型。
7.2.1指向概念KC1、SC2.1的问题
问题1:实验时向100 mL的培养液中接种1 mL菌种,1 mL菌种中含有7×107个酵母菌,培养12 h酵母菌的数量是多少?
针对此问题,学生提问:“酵母菌生殖方式是什么?繁殖一代需多长时间?”
教师指出:“在实验室设置的培养条件下酵母菌1.5 h繁殖一代,即一个酵母菌从孕育出芽到芽体脱落成一个独立的个体需要1.5 h。1.5 h 1个酵母菌可以变成2个。”
学生列出的过程如下:
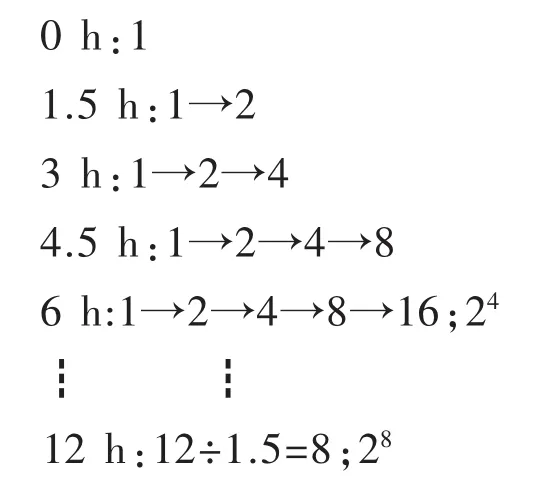
1 mL菌种中含有7×107个酵母菌,12 h酵母菌的数量是 7×107×28。
教师提问:“假设酵母菌的初始数量是N0,培养t小时后,酵母菌数量Nt是多少?”(学生回答:Nt=N0×2t/1.5。)
教师追问:“公式中2的含义是什么?”(学生:2表示1个变成2个。)
显然学生理解不透彻,为了让学生正确理解,教师再问:“t/1.5的含义是什么?2还可以有什么含义?”(学生:2代表的是下一代数量是上一代数量的倍数,或是单位时间的增长倍数。)
这时学生对于数学公式中字母代表的生物学意义才能理解透彻。
教师设问:①如果用λ表示单位时间种群数量的增长倍数,初始数量是N0,培养t时间,种群数量 Nt是多少?(学生:Nt=N0λt。 )
②以时间为横坐标,种群数量为纵坐标,上述公式表示的种群数量变化曲线是什么样的?
学生绘制的曲线如图1。

图1
教师指出:曲线和公式中描述的种群数量增长的规律,称其为种群数量增长的“J”型曲线。
通过以上分析过程,师生一起归纳种群数量变化的规律,并用公式或曲线等数学形式表示,形成概念KC1。
问题2:酵母菌的数量出现上述曲线中的变化趋势,需要的条件是什么?
学生:“需要不断补充营养物质,不断扩大培养空间。”另一位学生补充:“是无限的空间和资源。”由此,学生深刻理解概念SC2.1。
通过教师的提问,学生分析、归纳、总结,将种群数量的变化用数学形式进行描述,并赋予数学模型生物学意义。
7.3学生进行实验构建种群增长的“S”型曲线
7.3.1学生实验操作实验室培养的酵母菌,种群数量的变化会不会出现 “J”型曲线?不需要学生回答,学生的任务是:对不同培养时间的酵母菌进行计数,收集、整理数据,绘制曲线。
1)学生分组:将全班学生平均分成7组,分别对培养 0 h、2 h、4 h、6 h、8 h、10 h、12 h 的酵母菌进行计数,每组只对其中一个培养时间的酵母菌计数。
2)制作装片:(略)
3)计数、汇总数据:每组每人记录一个血球计数板中2个计数室的10个中方格,将小组所有学生计数得到的所有中方格中的酵母菌数目求平均值,利用求得的平均值,计算100 mL菌液中酵母菌数目,计算公式如下:
酵母菌数目/100 mL菌液=平均值×25×104×稀释倍数×100
将每组计算得到的100 mL菌液中酵母菌数目输入表2中。

表2 酵母菌种群数量随时间的变化
将表2中数据用Excel转换成曲线图,得到一定体积培养液中,一定培养条件下酵母菌种群数量变化的曲线。图2是2016年3月29日高二4班学生绘制的酵母菌种群数量变化曲线。

图2 酵母菌种群数量的变化

图3 酵母菌种群数量的变化

图4 酵母菌种群数量的变化
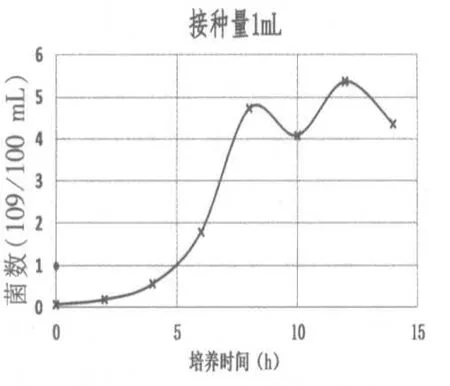
图5 酵母菌种群数量的变化
图 3、图 4、图 5分别是 2016年 3月 29日高二 1班、2014年 4月 16日高二1班、2015年 5月10日教师实验得到的酵母菌种群数量变化曲线。多次实验发现,酵母菌数量变化都出现了类似英文字母“S”形状的变化规律,这样的增长称为种群增长的“S”型曲线。教师引导学生回顾构建模型过程包括:确定研究课题;设计方案;实施方案;收集、统计、整理、分析数据;构建模型;多次重复实验验证模型。
学生亲身经历构建模型的过程,体会到真实、直观、形象的实验结果。
7.3.2分析模型利用实验构建的模型,建立、理解生物学概念。
7.3.2.1指向概念SC2.2形成的问题
问题1:综合几组实验结果,固定体积培养液,一定培养条件下,接种少量酵母菌,酵母菌种群数量增长有什么规律?
学生回答:“开始种群数量增长较慢,然后增长逐渐加快,后来增长又减慢了,最后种群数量趋于稳定。”
教师提问:“增长的快慢是增长速度还是增长率?”
学生在回答问题时,没有明确地想过是增长速度还是增长率,经教师提醒,学生意识到自己说的是曲线的斜率,是增长速度。
问题2:分析在不同培养时间段酵母菌种群数量变化趋势不同的原因,与出生率和死亡率的关系是什么?
学生回答:“初期营养物质充裕,生长条件适宜,酵母菌数量增长较快,出生率大于死亡率。随着营养物质的不足,酵母菌数量增长速度下降,逐渐达到出生率等于死亡率。”当学生面对一瓶瓶酵母菌菌液时,还能想到酵母菌代谢废物的积累,酵母菌呼吸作用产生的CO2会改变培养液的pH,这些因素都会限制种群数量的增长。在分析时学生还提出,酵母菌数量最后应该下降,全部死亡或只有少量存活。
教师提问:“为什么一段时间后,种群数量的增长速度会加快?”
学生回答:“因为初期,种群数量的基数在逐渐增大,所以单位时间内增长的数量增加。”
教师总结:像今天出现的种群数量增长的“S”型曲线在数学上也有曲线跟它非常拟合,数学上的这种曲线也可以用公式表示。
问题3:实验结果为什么没有出现种群增长的“J”型曲线?如何改进实验才能得到“J”型曲线?
学生根据实验分析得出:种群数量增长出现“J”型曲线还是 “S”型曲线,取决于种群生存的环境和资源条件。
在分析指向概念SC2.2问题的过程中,学生的思维从表象到本质,从感性认识上升到理性认识,深化对科学规律的理解,认识到在不同环境、资源条件下种群数量变化的规律不同。
7.3.2.2指向概念SC2.3、SC2.4形成的问题
问题1:实验结果显示,酵母菌数量达到最大后,出现了波动,请分析出现这种波动的原因是什么?
学生刚开始思考时有些困难,通过不断交流讨论,有学生提出:可能是酵母菌具有很强的耐受性,并可利用死亡酵母菌的残留物作为营养物质。当营养物质减少时酵母菌的死亡率大于出生率,种群数量下降。死亡的酵母菌又为活的酵母菌提供新的营养物质,腾出生存空间,又使得出生率大于死亡率,酵母菌的数量增加,所以会出现波动。由此,理解概念SC2.4。
问题2:分析实验结果,在100 mL的培养液中能维持的酵母菌的最大个体数是多少?
有的学生依然会答曲线中最高点的数量,这时教师要提示“维持”的最大个体数,学生就会想到是在一个最大值附近波动,这个最大值就是培养液中能维持的酵母菌的最大个体数。归纳出概念SC2.3,教师给出“环境容纳量”这个术语。
问题3:如果锥形瓶换成500 mL,增加培养液的体积,种群相对稳定的个体数会不会改变?为什么?
学生很容易理解:环境条件改变,环境容纳量也会改变。
通过3个层层深入的问题,引导学生不断思考和感悟,理解概念SC2.3。
7.3.3指向概念SC2.2、概念SC2.3理解的问题在自然环境中也存在这种变化规律,大约在1800年,人们将绵羊种群引入澳大利亚塔斯马尼亚岛。之后,统计了在100年间塔斯马尼亚岛上绵羊种群数量的变化,如图6。

图6 塔斯马尼亚岛绵羊的数量变化
问题1:分析绵羊种群数量变化为什么会出现类似“S”型变化规律?
学生分析并不困难,教师要追问:在自然种群中,环境和资源有限的条件下,种群数量经过一定时间的增长后趋于稳定,这里的“环境和资源有限”与固定培养液培养酵母菌时 “环境和资源有限”的含义是否相同?
学生在分析、回答时体会到:自然种群中单位土地面积、单位时间内植物固定有机物的量是一定的,培养酵母菌时资源用完就没有了。教师再追问:这种环境资源的不同,注定了2个种群最终的命运有何不同?学生体会到在相对稳定的自然生态系统中,种群数量会一直在K值附近波动。
问题2:如果人们在塔斯马尼亚岛过度放牧,塔斯马尼亚岛对于绵羊的容纳量是否会改变?分析原因是什么?
学生在分析的过程中领悟到环境条件被破坏,环境容纳量会改变。
在教师创设的新情境中,学生运用学习的概念,分析问题,加深对概念SC2.2、概念SC2.3的理解。
7.3.4指向概念SC2.4理解的问题
问题:出示1913—1961年间东亚飞蝗种群数量变化的曲线,这种变化属于什么型增长?
学生基于对种群增长的“S”型曲线和环境容纳量的理解,可以回答出此曲线是在K值附近的波动。
教师提问:“造成这种波动的原因可能有哪些?”
学生能够分析出气候、食物、天敌等原因。在分析过程中,学生领悟到种群数量趋于稳定后,由于外界生物因素和非生物因素的影响,种群数量会在一定范围内出现波动,理解概念SC2.4。
7.4种群数量变化规律在生产生活实践中的应用教师讲解种群增长的“S”曲线中增长速度和增长率的变化规律。
问题1:根据图7分析渔民养鱼,鱼池中鱼的种群数量增长到什么时候适宜捕鱼?捕多少鱼才能获得最大持续捕获量?为什么?教师要解释“最大持续”的含义。(学生:在D点进行捕鱼,捕捞后剩到A点。)
教师:“为什么在D点进行捕鱼,而不是B或C点?”(学生:D点的数量最多。)
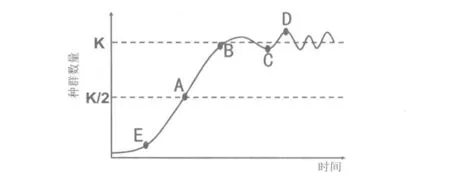
图7
根据学生的回答,说明学生对于种群数量变化规律的应用出现了问题。教师引导:“种群从A点增到B点的时间,与从B点增到D点的时间相比哪段所用时间长?哪段时间种群数量增长多?”“在实际生产中,如何确定种群数量达到了D点?种群的K值可以预测吗?”在教师的引导下,学生体会到B点是最佳捕鱼点。
问题2:根据图7分析,若是捕获老鼠,应在何时进行捕获,老鼠的种群数量应控制在哪个范围?灭鼠的措施有哪些?
学生能够分析出捕鼠越早越好,种群数量要控制在E点内。
以上2个问题是从2个不同的角度应用种群数量的变化解决问题。
8 教学反思
在开展探究性实验过程中,学生带着问题在做中思、做中学、做中悟。实验过程是学生获取证据、回答问题的过程,是形成和深入理解重要概念的过程。实验为学生更好地形成和理解重要概念提供了丰富的事实性知识、情境。
课堂教学设计问题时应从实验条件、实验操作和实验结果出发,问题的答案落在对概念的理解上。学生在思考、分析问题时,不断回顾实验操作和实验结果形成的条件,有助于深入理解重要概念。
[1]中华人民共和国教育部.普通高中生物课程标准(实验).北京:人民教育出版社,2003.
[2]牛翠娟,娄安如,孙儒泳,等.基础生态学.2版.北京:高等教育出版社,2007:79.
[3]杨文源,刘恩山.为了理解的教学设计:从指向核心概念的问题开始.生物学通报,2014,49(1):28.
[4]刘恩山,张颖之.课堂教学中的生物学概念及其表达方式.生物学通报,2010,45(7):40.
[5]李红菊,刘恩山.中小学生物学课程中生态学重要概念的筛选及其表达.生物学通报,2010,45(10):31.
