基于M—K方法及成分提取的海洋表层热状分析

韩心娅+沈翀+沈婷婷+程宗毛

摘要：本文针对东海一点的9年海表温度遥感数据集的序列（2003-2011）进行处理，首先通过SPSS初步检验出所处理的温度数据满足正态性。然后通过Mann-Kendall秩次相关检验研究了数据点温度的趋势性和突变性。通过周期存在性检验取定四个周期。用傅里叶函数描述周期成份，各自系数分别通过参数估计得到。对比测试数据的周期项和原始数据图表得结果有效。该随机序列的自相关是拖尾的，而偏相关是一阶截尾的，故可建立AR（3）模型，分析得序列是白噪声序列。

关键词：海表温度；Mann-Kendall方法；趋势性；突变性；周期成分

1.引言：时间序列分析是概率统计学科中的一个分支，随着基本理论的更加深入和完善，以及统计软件技术的发展，使其在气象水文等领域有了更加广泛的应用。海表温度不仅是描述海洋表层热状况的重要指标，其异常情况还是海洋影响大气环流、气候变化的主要因子。所以海表温度一直都是诸多学者观察、研究和预测的重要研究对象。趋势性、突变性和周期性是时间序列数据的基本特征， Mann-Kendall方法作为一种非参数统计检验方法，其优点在于样本不需遵从一定的分布，也不会受少数异常值的干扰，计算相对方便。近几年被广泛用于气温、降水量变化 、植被变化等自然界变化的趋势分析中，考虑到海表温度的变化规律也有相似的性质。因此，本文选择通过处理海表温度使其可以显示出正态性，而后引入该M-K方法测试数据在一定时间段内是否异常，在此基础上再进一步提取海表温度集的周期成分，确立时间序列模型。

2.数据预处理

本文考慮建立合理的分析模型提取海洋表层温度数据的趋势性、周期性和突变性特征，通过误差分析比较不同提取方法的优缺点，为预测海表温度未来的变化提供更加有效的依据。此外，将温度数据集进行合理的区间划分，使得每个区间内的统计数据复合最优的正态分布统计，并给出正态分布的检验方法、统计区间的上下节点及统计分布模型的相关参数。

本文采用了东海海表上2003年至2011年一研究点的温度遥感数据集，从1开始编号，共计数据3287个。计一年为365天，这组数据记录了9年里每一天的温度，但是由于2004年和2008年是闰年，为减小不同年份的对比差异，将这两年2月29日的温度数据剔除。推算可得这两个时间点的温度数据对应的序号分别为425和1886，剔除后数据长度变为3285。

几乎所有的科研数据都必须满足正态性才能进行分析，因此要对数据进行正态性检验，以保证后续分析的可靠性。本文利用SPSS对每个点每一年的温度数据进行了直方图和正态曲线绘制，具体将东海2003年的情况呈现如下：

观察图1可得数据呈正态分布。图2给出了K-S检验的具体结果，由于概率p值为0.227，大于0.05，故不能拒绝K-S检验的原假设，即数据满足正态性。这为接下来的探讨提供了一定的支持和帮助。

3.海表温度基本特征分析

3.1 Mann-Kendall方法简介。Mann-Kendall方法由于最初由H.B. Mann和M.G.Kendall提出原理并发展了该方法。当时这一方法仅用于检测序列的变化趋势，后来经他人进一步完善和改进，才形成目前的计算格式。该方法既可以检测序列的变化趋势，也可以进行突变点检验。

3.2 Mann-Kendall方法应用

3.2.1 研究点海表温度的日变化趋势与突变情况。在对东海表温度的数据的趋势性和突变性信息进行提取时，本文主要采用M-K方法，通过matlab软件编写程序，我们得到下述结果：

①趋势变化：

②突变情况：

③结果分析：一般而言M-K方法计算的趋势符合正态分布，且Z= 4.381>1.96，则说明该点海表温度的日变化趋势有明显上升趋势。UFK和UBK在95%的信度线之间没有交点，说明该点温度在这段期间内没有突变。

3.2.2 研究点海表温度的年变化趋势与突变情况

①趋势变化：

②突变情况：

③结果分析：Z statistic = 0.31277<1.96，说明该点温度的年变化趋势有上升但不明显。UFK和UBK在95%的信度线之间有交点，且致在8-9年之间，说明该点海表温度在第八年左右发生突变，且该点表温度由下降趋势转为上升趋势。

3.3 周期成分识别

3.3.1 周期显著性判断。首先我们用方差分析法判断时间序列中是否存在显著周期。在分析周期之前，事先并不知道这一序列的周期是多少，所以要根据序列长度，列出可能存在的周期。若时间序列总长度为n，则可能存在的周期为。将周期为T的时间序列进行分组，对应可以分为组数据，根据

可知第i组的平均值为：

上式中ni表示第i组内的数据个数。

将时间序列分别按每一个可能的周期进行分组，计算相应的组内离差平方和SE及组间离差平方和SA：

上式中表示第i组的平均值，表示总平均值。

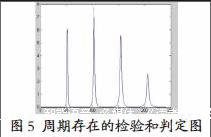
可以证明服从自由度为的F分布。给定显著性水平，查分布表可以得到的值，如果，则此周期为显著周期。由于与真实周期相邻的值有可能通过显著性检验，我们取连续通过F检验的T值中使F值最大的对应T值作为主周期。用测试数据测试检验周期的存在和判定周期：

从图5中可以看出当t=52，103，154，206时F值最大，故我们取定这四个周期。

3.3.2 周期提取。周期确定后， 周期成份Pt可用如下形式也即傅里叶函数描述：

上式中d表示有效谐波数即主周期的个数，Ti表示第i个谐波对应的周期，ai和bi为参数，计算式为：

根据傅里叶函数求系数的公式，对其参数进行估计得到：

从而得出测试数据的周期项和原始数据的对比图，从而计算得到随机项图，具体如下所示：

用Eviews对随机项做ADF检验，检验结果如下表所示：

从上图中可以看出，该随机序列通过ADF检验，是一组平稳序列。再对随机序列进行相关分析，看其是否相关，从而判定它是否是白噪声。

从图9可以看出，该随机序列的自相关是拖尾的，而偏相关是一阶截尾的，故可建立AR（3）模型，模型建立结果和残差序列如下所示：

由图11和图12可知，该残差序列在5%的置信区间内平稳且不相关，故为白噪声序列。

总结：本文通过SPSS初步检验出所处理的温度数据满足正态性。继而通过Mann-Kendall秩次相关检验发现东海表层温度的年变化趋势虽然在第八年有突变，海表温度由下降趋势转为上升趋势，但近9年整体无明显变化的趋势。而在日变化趋势上则有明显的上升趋势。周期存在性检验中，t=52，103，154，206时F值最大，故我们取定这四个周期。周期成份可用傅里叶函数来描述，4个周期下系数则可分别通过参数估计得到。测试数据的周期项和原始数据对比图表明所得结果有效。该随机序列的自相关是拖尾的，而偏相关是一阶截尾的，故可建立AR（3）模型，分析得序列是白噪声序列。