汤旺河流域主要测站年径流量随机性与趋势性分析

2010-06-26肖鹏云李敬东田长涛

黑龙江水利科技 2010年1期

肖鹏云，李敬东，田长涛

(1.佳木斯水文局，黑龙江佳木斯 154002;2.伊春水文局，黑龙江伊春 153000)

1 前言

在实际工作中，为了进一步分析、预测某一水文要素的变化规律，经常会建立一些水文数据分析、模拟数学模型。在根据随机水文学原理和分析技术对水文要素系列数据建立分析模型时，为了了解资料系列有无明显的系统性影响和趋势性的存在，要对数据系列进行必要的随机性和趋势性检验，然后才能建立数据分析模型。本文以汤旺河流域控制面积较大的5个主要测站为例来分析各站年径流量数据的随机性和趋势性特征，各站资料系列情况见表1。

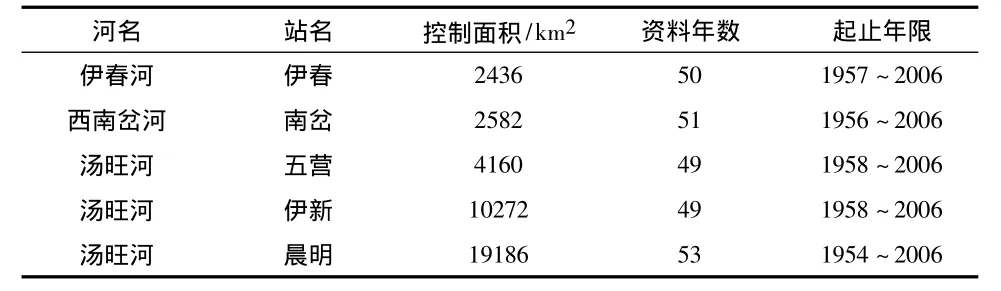
表1 选用测站一览表

2 资料系列随机性的统计检验

随机性的统计检验通常采用转折点检验法。本法是检查数据系列高值和低值(相对于邻值而言)的个数。在实测系列 Xt(t=1，2，…，n)中，如果 Xi大于 Xi-1和 Xi+1或小于两相邻值，则在t=i处出现转折点P。对于3个不等的观测值，这种数量次序的6种可能情况是:

①Xi-1＞Xi＞Xi+1;②Xi+1＞Xi＞Xi-1;③Xi＞Xi-1＞Xi+1;④Xi+1＞Xi-1＞Xi;⑤Xi＞Xi+1＞Xi-1;⑥Xi-1＞Xi+1＞Xi。

在随机系列中，6种情况具有相同的出现概率。除了①、②之外，转折点均可出现，其出现的可能性是2/3。因为转折点不可能出现在t=1和t=n处，因此随机系列中转折点的期望个数为:

E(p)=(n-2)×2/3。同时可证明转折点P的方差为:Var(P)=(16n-29)/90;所以，P可以标准化，即Z=[P-E(P)]/[Var(P)]1/2近似为标准正态变数[1]。

由于太多或太少的转折点表明为非随机性，所以采用双尾的显著性检验，显著性水平设为5%，相应的判别标准值为-1.96～1.96。各站资料的随机性检验计算结果(参见表2)表明，各站Z值均在判别标准范围内。从而表明，各站年径流量系列中具有随机性的原假设在5%的显著性水平下不能拒绝，即表示实测资料系列具有一定的随机性。

3 资料系列趋势性的统计检验

趋势性的统计检验采用肯德尔(Kendall)的秩次相关法，此检验也称τ检验，是以连续观测值超过某特定值的个数(记为P)的一种检验。例如，某水文要素系列X1，X2，…，Xn，假定它是连续增加的(上升趋势)，那么，先以X1为比较特定值，其右边值大于X1的有n-1个，再以X2为比较特殊值，其右边的值大于X2的有n-2个，余此类推，可以得到以X3，X4，…，Xn-1为比较特定值时，其右边值大于 X3，X4，…，Xn-1的个数分别为n-3，n-4，…，1。这样得到总数 p=(n-1)+(n-2)+…+1=(n-1)×n/2。如果系列值全部倒过来，则p=0。由此可知，对于无趋势的系列，E(p)=(n-1)×n/4。趋势性检验的基础是统计量:τ=4P/[n(n-1)]-1。对于随机系列有:E[τ]=0，亦可证明:Var(τ)=[2(2n+9)]/[9n(n-1)]，且 Z= τ/[Var(τ)]1/2，Z 在 N 增加时很快收敛于标准者正态分布[2]。

趋势性检验的显著性水平设为5%，相应的判别标准值为“-1.96～1.96”。各站资料的趋势性检验结果(参见表3)表明，伊春、南岔、伊新三站年径流量无趋势性的原假设在5%的显著性水平下不能拒绝。至于五营、晨明没有通过趋势检验的测站，可由P是否接近(n-1)×n/2或0两种极端情况来做进一步检验判断[2]。五营站n=49，p=(n-1)×n/2=1176，表3中实际p=385。晨明站n=53，p=(n-1)×n/2=1378，表3中实际p=521。两站的实际p，既不接近(n-1)×n/2，也不接近0这两种极端情况。说明其上升或下降趋势不十分明显，仍可将其划归于无明显趋势之列。