超高多肢斜拉桥桥塔气动力系数研究

何旭辉，方东旭，王汉封，李　欢

(1.中南大学 土木工程学院，湖南 长沙　410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙　410075)

随着桥梁施工技术、计算水平和材料性能的快速发展，斜拉桥因其造型美观、造价经济、施工方便、跨越能力强等优点得到了飞速发展，被认为是跨径在200～1 000 m范围内最适宜的桥梁形式[1-4]。随着斜拉桥跨径的逐步增大，与其相适应的超高桥塔的建设是桥梁发展的必然趋势，目前世界上大多数桥塔高度不超过250 m，塔高300 m以上已属于超高桥塔范畴[5-6]。大跨斜拉桥本身就是一种在风载作用下易发生振动和变形的柔性结构，塔高的增加导致结构变得更柔、阻尼更小，又由于施工阶段没有拉索的约束，其施工阶段抗风稳定性比成桥状态更低，因此桥塔自立状态下的抗风性能已经成为影响其设计和施工的控制因素[7-9]。

桥塔的风致响应主要包括静风稳定性、涡激共振、驰振和抖振等，而桥塔气动力系数是抖振、驰振、静风稳定性分析与静阵风荷载计算的基础参数，因此气动力系数是研究桥塔抗风最为重要的内容之一[10]。目前获得气动力系数主要有3种方法，即现场风压实测、数值模拟计算、风洞测力/测压试验。现场风压实测受测点布置、仪器安装和天气条件等限制很难获得准确数据。数值模拟计算较难保证存在明显三维空间流动效应复杂桥塔计算结果的准确度。风洞测力/测压试验具有一定的普遍性和准确性，是结构风载静动力分析的最根本方法。但一般来讲，风洞测力试验仅能得到结构整体气动力。禹见达等[11]通过现场实测得到了洞庭湖大桥塔顶的风场和风压特性，研究了风压系数和风场湍流度等，但其仅测试了塔顶1个断面的风压时程，结果不能很好地反映实塔情况，参考价值有限；李胜利等[12]通过数值模拟的方法计算了门型桥塔静气动力系数和驰振力系数，得到两塔柱间气动干扰对气动力系数影响明显的结论，但未说明具体的影响趋势，忽略了气动干扰的雷诺数效应；李永乐等[13]通过刚性模型风洞测力试验，测试了独柱式变截面倾斜桥塔的气动力系数，分析了桥塔三维绕流的影响，但文中假定阻力系数沿高度线性变化可能会引起一定误差；陶齐宇等[14]通过刚性模型风洞测力试验研究了H形桥塔气动力系数的雷诺数效应和随风偏角的变化规律，但其节段气动力是在假定各断面具有相同气动力系数的基础上得到的，加之塔柱间可能存在干扰效应，故其结果可能与实际存在较大误差。目前国内外鲜有采用风洞刚性模型测压试验进行桥塔气动特性研究，所分析桥塔多不属于超高桥塔，并且主要为两肢柱结构形式，对4根肢柱桥塔的气动特性和干扰效应的研究十分有限。

本文针对某拟建大跨度山区超高斜拉桥桥塔，通过风洞刚性模型测压试验，研究桥塔整体与塔柱节段气动力系数随风偏角和风速的变化规律，分析不同肢柱数量的气动干扰效应及其对整塔的影响。

1　工程背景

某拟建大跨度山区超高三塔双索面斜拉桥的跨径布置为(249.5+550+550+249.5)m，全桥总长为1 599 m，三塔高度分别为320，328和298 m，中塔高度仅比法国米约大桥最高塔低15 m，居世界第二；桥塔全部暴露在大气中，桥面与河流平均水位的垂直距离高达292.3 m，超越法国米约大桥，居世界第一，桥塔结构及截面形式如图1所示。图中：B为顺桥向宽度；D为横桥向宽度；d

为横桥向肢间距；b为顺桥向肢间距；β为截面外轮廓对角线与横桥向的夹角；γ为截面外轮廓对角线与顺桥向的夹角。

图1　桥塔结构形式及各节段尺寸图(单位：m)

根据该桥塔肢柱数量的变化特点，将桥塔沿高度方向划分为4个节段，不同节段截面尺寸信息(部分结果取整数)见表1。截面倒角半径r均为0.5 m。

表1　中塔截面信息

注：Ai为各节段顺桥向投影面积。

采用大型通用有限元软件Ansys建立桥塔自立状态模型进行动力特性分析，桥塔自立状态自振频率见表2。由表2可知，最不利桥塔为中塔，其1阶弯曲(横顺桥向)、扭转频率均最低，故取中塔为试验研究对象。

表2　桥塔自立状态自振频率　Hz

2　桥塔刚性模型测压试验

桥塔刚性测压模型不考虑结构的气弹效应，严格遵循气动外形相似，包括截面倒角等的模拟。模型采用1∶225缩尺比，高1.493 m(含承台)，各个部分尺寸均按照缩尺比加工，由厚3 mm高强有机玻璃板激光切割拼装而成。桥塔模型与风洞底转盘系统刚性连接，并用2根φ1.5 mm钢丝将模型顶部与风洞壁相连，保证模型在试验过程中未发生任何振动。桥塔测点共布置250个，分布在19个截面上，其中最大横向积分长度约为47 mm，最小约为18 mm，测点截面分别位于各个节段的两端和高度的三(四)等分处，试验测压模型、坐标系定义及测点布置如图2所示。图中：v为风洞来流风速；θ为风偏角；FH，FV和MT为体轴坐标系下气动力分量；FD，FV为风轴坐标系下气动力分量。

本试验在中南大学高速铁路建造技术国家工程实验室——风洞实验室高速段(高3 m，宽3 m，长15 m)进行，该风洞为双试验段回流式低速风洞，其中高速试验段风速在0～94 m·s-1范围内连续可调，湍流度小于0.5%。由于桥塔沿轴线中心对称，故试验风偏角分别取为0°(顺桥向)，15°，30°，45°，60°，75°和90°(横桥向)。试验风速分别为5，10，15，20，25，30和35 m·s-1共7种风速，特征尺寸取桥塔模型横桥向宽度(50.5～176.0 mm范围变化)，对应雷诺数变化范围为Re=1.7×104～4.1×105。试验中将皮托管固定于1.4 m高度处进行塔顶实际风速测量。用内径0.6 mm、长度约1 m的测压管将模型表面测压孔与4个DSM3400电子式压力扫描阀相连，对250个测点进行同步测量，扫描阀分别置于桥塔第4节段内和风洞底的转盘中，设定采样频率为625 Hz，各测点采样点数均为2万个。通过扫描阀测量桥塔塔身风压分布，对面积分得到整塔以及各个节段塔柱的三分力系数时程和风载。

图2　试验测压模型与坐标系定义

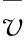
图3　风洞自由流无量纲时均风速沿高度方向分布

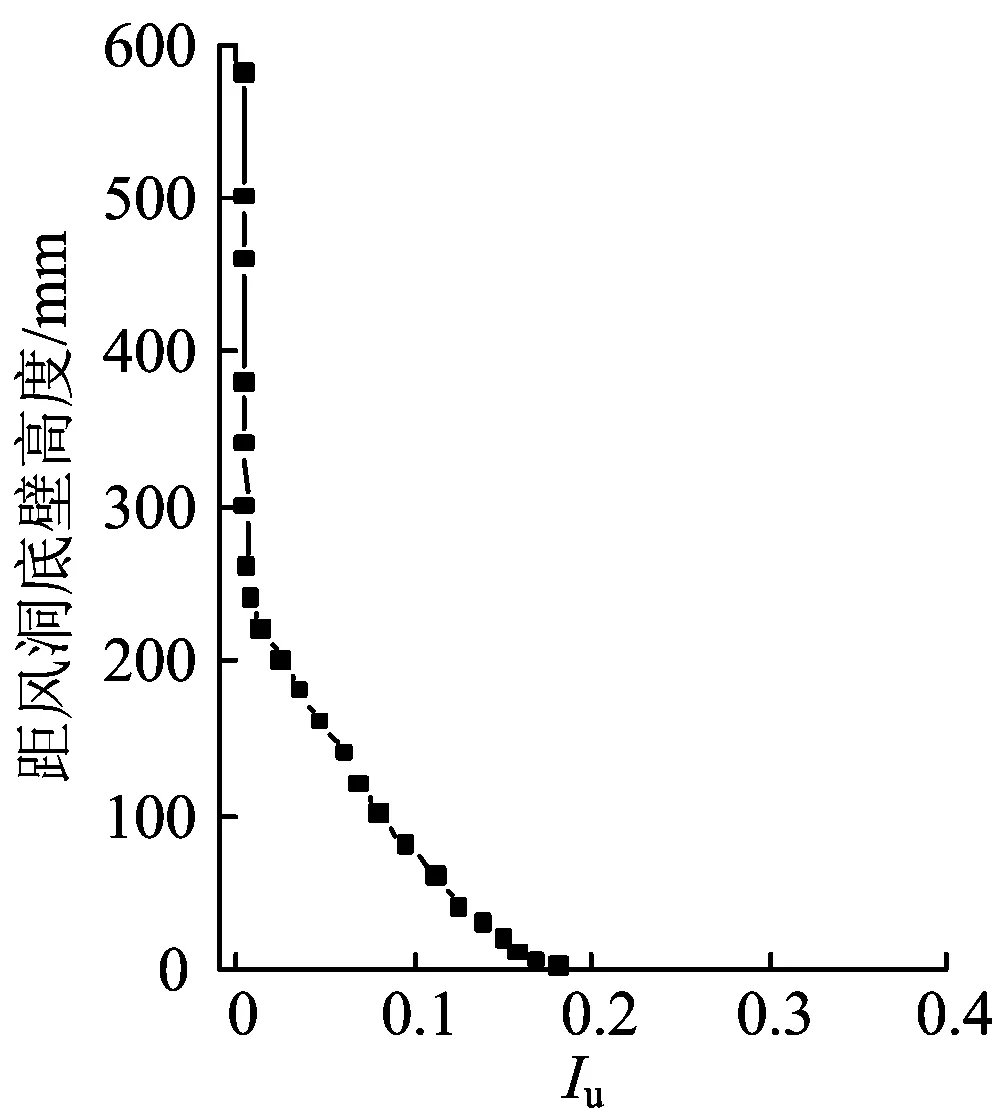
图4　风洞自由流湍流度Iu沿高度方向分布

3　桥塔气动力及干扰效应分析

3.1　桥塔整体气动力分析

体轴坐标系下三分力系数的计算式为

(1)

(2)

(3)

其中，

CPi=(Pi-P∞)/(P0-P∞)

式中：CH，CV和CM分别为体轴坐标系下阻力系数，升力系数和扭矩系数；ρ为空气密度，取1.225 kg·m-3；A为模型在0°风偏角时的迎风投影面积，计算整体气动力系数时取整塔投影面积，计算各节段气动力系数时取各节段对应投影面积；Si为测点i的积分面积；αi为测点i的外法向量在XOY平面内投影与X轴的夹角；Bi为测点i所处截面的截面宽度，取桥塔在0°风偏角时对应截面的整体轮廓宽度；CPi为测点i处的风压系数；Pi为试验测点的风压；P0为风洞总压；P∞为风洞静压。

试验分析采用风轴坐标系下气动力系数，其与体轴坐标系下的气动力系数转换公式为

(4)

式中：CD，CL为风轴坐标系下阻力系数和升力系数。

桥塔整体三分力系数直接影响着桥塔的静力稳定性，对桥塔气动特性分析具有重要意义。图5和图6分别为桥塔整体气动力系数CD，CL和CM随风偏角和风速的变化曲线。

由图5和图6可知：桥塔整体阻力系数CD随风偏角的增大逐渐减小(最大值约为1.6)，随来流风速增大整体变化不明显，但在风偏角为30°和60°时随风速增大有较明显的增大趋势；升力系数CL随风偏角的增大呈现先减小后增大再减小的变化趋势，在风偏角为30°和75°时出现峰值，当为30°时，升力系数CL的绝对值最大(约为0.3)；扭矩系数CM随风偏角的增大先增大后减小再增大，整体随雷诺数变化不显著，在30°和75°风偏角时，扭矩系数CM出现峰值，在75°风偏角时绝对值最大为0.1，其中90°风偏角下CM与风速呈现明显类似正弦曲线关系，这可能是由于肢柱间产生的窄缝射流[15-16]，因科恩达效应使尾流出现交替反相位旋涡脱落，引起气动力系数不稳定且雷诺数效应明显增强，又加之截面倒角或安装存在初始偏角，诱导气动力系数随风速呈现类似正弦函数变化，此规律在1节段、2节段和3节段的升力系数和扭矩系数中均有出现。对比文献[12]中的门型桥塔整体气动力系数，由于存在多肢干扰，倒角阻力系数随风偏角的变化趋势和取值范围(1.0～1.8)相近，但升力系数差别较大，主要原因是由于本文桥塔更加复杂，多肢干扰引起的会向气动不稳定更明显。可见，气动干扰对于塔柱整体气动力系数存在影响，其中对升力系数变化趋势的影响大于阻力系数。综合考虑，30°风偏角为最不利风偏角。

图5　桥塔整体气动力系数随风偏角变化曲线

图6　桥塔整体气动力系数随风速(雷诺数)变化曲线

3.2　塔柱气动力及干扰效应分析

Melbourne等[17-18]研究表明上游单体建筑的干扰作用对下游建筑的影响明显，可使其顺风向和横风向的基底弯矩最大值分别增加30%和70%；Surry等[19]通过风洞试验证明下游高层建筑导致目标建筑的局部风压增加了近3倍；Kwork和Khanduri等[20-21]对高层建筑风荷载的干扰效应进行了较为详细的综述，表明任何结构均有可能遭受与其尺寸相近的邻近结构引起的荷载作用，由此可见塔柱间必然存在干扰效应且不能忽略。为了进一步分析塔柱多肢干扰效应对气动力系数的影响，对桥塔的4个节段同步测压，得到各个节段的三分力系数随风偏角和 风速(雷诺数)的变化，如图7—图14所示，图中三分力系数下标中的1～4对应4个节段，其中第4节段为类独柱结构，通过与规范[22]对比可知，0°和90°风偏角下阻力系数与规范理论值相近，一定程度验证了试验结果的可靠性。

由图7—图10可以看出：1和2节段的气动力系数与桥塔的整体气动力系数差别较大，其中1和2节段的阻力系数、升力系数随风偏角的增大均先增大后减小，扭矩系数变化趋势与整体相同。1和2节段的阻力和升力系数为最大值时的风偏角θ均处于相应截面的β～γ角度范围内，并且2节段的CD明显大于1节段，2节段的CL变化复杂程度大于1节段。可见，气动干扰效应对阻力系数和升力系数的影响较大，4肢干扰效应明显大于2肢干扰。

图7　1节段塔柱气动力系数随风偏角变化曲线

图8　1节段塔柱气动力系数随风速(雷诺数)变化曲线

图9　2节段塔柱气动力系数随风偏角变化曲线

图10　2节段塔柱气动力系数随风速(雷诺数)变化曲线

对比图7—图8和图11—图14可见：由类似两“邻近薄板”组成的3节段的气动力系数变化趋势更接近于独柱式结构(4节段)，其阻力系数最大值均出现在遮挡面积较大的0°风偏角；当风偏角θ>β时，3节段的CD明显小于4节段，并且3节段CD在90°风偏角时最小，3节段的CL和CM整体均大于4节段，这可能是因为肢间距较小时，尾流涡脱对背风肢柱的迎风面影响较小且产生了负压区，同时，由于“窄缝射流”引起横向气动不稳定增强，引起升力系数和扭矩系数增大。可见，随着肢间距的减小，2肢柱干扰效应对气动力系数的影响逐渐减小，气动力系数接近于独柱结构；相比独柱结构，肢间距较小时其阻力系数偏小，升力系数和扭矩系数增大；独柱结构的阻力系数最大值一般出现在0°风偏角(投影面积较大向)时，且大体上随风偏角变化呈减小趋势，而升力系数和扭矩系数一般较小。

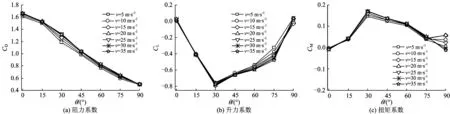
图11　3节段塔柱气动力系数随风偏角变化曲线

图12　3节段塔柱气动力系数随风速(雷诺数)变化曲线

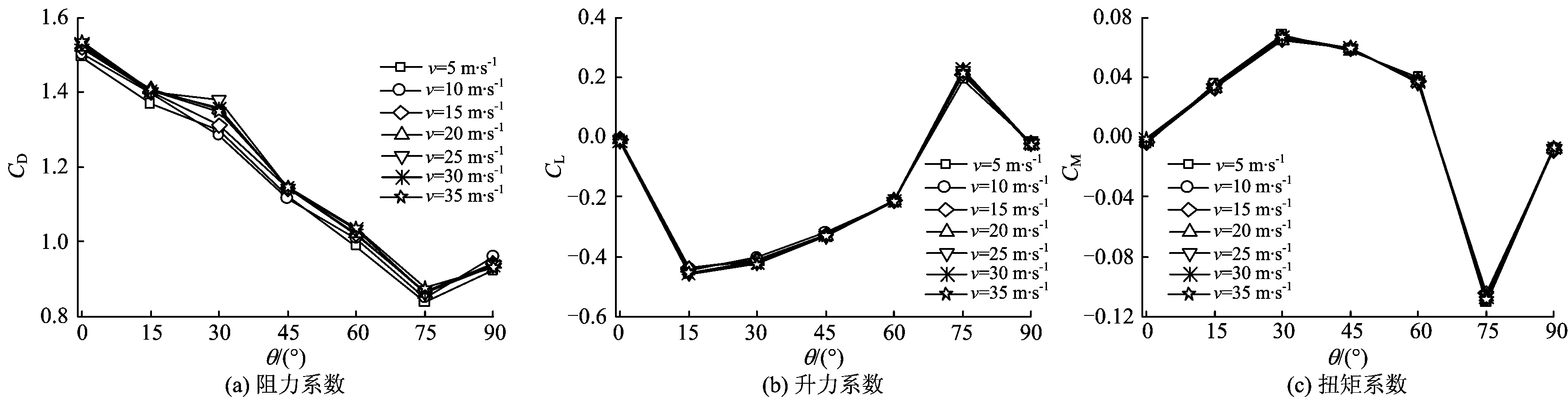
图13　4节段塔柱气动力系数随风偏角变化曲线

图14　4节段塔柱气动力系数随风速(雷诺数)变化曲线

对比图7—图14可以看出：1，2和3节段由于存在多塔柱的干扰导致其气动力系数的雷诺数效应更加明显，其中阻力系数随雷诺数的增大呈递增趋势，不同风偏角下升力系数和扭矩系数的变化趋势差别较大，但当风偏角达到一定值时，干扰尾流引起背风侧肢柱的迎风面和侧面的风压平均值变化增大，出现随雷诺数呈类正弦函数的关系。

3.3　桥塔最大气动力分析

上述对桥塔整体及各节段的气动力进行分析，得到了此类桥塔气动力变化趋势与变化范围、塔柱多肢干扰效应的雷诺数效应规律和随风偏角的变化情况，但实际桥塔设计施工中更多关心的是最大气动力系数。图15为在试验风速范围内不同风偏角下最大气动力系数变化曲线。由图15可以看出：由于多肢干扰的影响，桥塔最大整体阻力系数大于独柱桥塔结构，而升力系数和扭矩系数反而有所减小，这是因为干扰效应的增强导致升力方向的改变，而使桥塔的整体升力系数和扭矩系数减小。

依据式(1)计算各节段所受阻力，表3所列为来流风速v=15 m·s-1时各节段所受阻力与整塔所受阻力的比值(阻力比)。由表3可以看出：尽管2节段的阻力系数最大，但阻力比最大的是4节段，约为43%，升力系数和扭矩系数的变化规律类似。可见，尽管多肢柱干扰现象对气动力系数的影响明显，但由于4节段的面积约占总塔面积的50%，因此面积最大的4节段对整塔三分力起主导作用。但考虑到自然风场中风速梯度与均匀流的不同，桥塔顶部节段所占整塔阻力比将大大增加，因此在进行此类桥塔整体和局部肢柱静力分析和设计计算中均应充分考虑多肢干扰的放大效应。

图15　试验风速下各气动力系数最大值随风偏角变化曲线

节段不同风偏角阻力比0°15°30°45°60°75°90°平均阻力比111.3013.0014.5016.5016.0013.4014.2014.10212.3013.6018.3022.1025.8028.0024.0020.60323.7022.6019.0016.5014.3013.6011.4017.30447.3045.1042.8039.9039.5040.8046.7043.20

4　结　论

(1)桥塔受多肢柱气动干扰的影响，整体阻力系数较独柱节段有所增大，升力系数和扭矩系数的绝对值相对减小；但多肢柱节段的气动力系数因干扰效应显著增大，阻力系数的增大尤为明显，在60°风偏角时最大值约为整塔的2倍。

(2)均匀流中面积最大的4节段对整塔气动力起主导作用(阻力约占整塔的43%)；但考虑到自然风场的特点，桥塔顶部结构所占阻力比将大大增加，在进行整体和局部肢柱计算时均应充分考虑多肢气动干扰效应。

(3)肢柱干扰效应主要表现在钝体结构三分力系数仍存在较明显的雷诺数效应。在试验研究的雷诺数范围内，阻力系数随雷诺数的增大缓慢增加，升力系数和扭矩系数随雷诺数的增大变化复杂，在某一定风偏角下，可能由肢柱间窄缝射流引起更为明显的雷诺数效应，出现随雷诺数呈类正弦函数关系变化。

(4)肢柱干扰效应引起的气动力系数变化较大，特别是干扰效应明显时气动力系数显著增大。1和2节段肢柱的阻力系数和升力系数随风偏角先增大后减小，最不利风偏角θ在β～γ范围内(见图1)；当2肢柱的间距较小(3节段)时，其气动力系数的变化规律与独柱结构(4节段)相近，阻力系数有所减小，升力系数和扭矩系数明显增大；独柱结构的阻力系数一般在0°风偏角时最大，其值可按照规范近似计算，而升力系数和扭矩系数一般较小。

[1]董聪，侯文葳，刘建华. 大跨度桥梁的造型设计[J]. 中国铁道科学，2002，23(3)：85-92.

(DONG Cong, HOU Wenwei, LIU Jianhua. Aesthetics and Design of Large-Span Bridges [J]. China Railway Science，2002,23(3)：85-93. in Chinese)

[2]程进，肖汝诚，项海帆. 大跨径斜拉桥静风稳定性的参数研究 [J]. 土木工程学报，2001，34(2)：55-61.

(CHENG Jin，XIAO Rucheng，XIANG Haifan. Study on Aerostatics Stability of Long-Span Cable-Stayed Bridges [J]. China Civil Engineering Journal，2001，34(2)：55-61. in Chinese)

[3]丁幼亮，胡心一，张志强，等. 考虑桥塔风效应的多塔斜拉桥抖振响应分析[J]. 工程力学，2014，31(10)：77-84.

(DING Youliang，HU Xinyi，ZHANG Zhiqiang，et al. Buffeting Response of Multi-Tower Cable-Stayed Bridge Considering Bridge Tower Wind Effects [J]. Engineering Mechanics， 2014，31(10)：77-84. in Chinese)

[4]WANG P H，TANG T Y，ZHENG H N. Analysis of Cable-Stayed Bridges during Construction by Cantilever Methods [J].Computers and Structures，2004，82(4)：329-346.

[5]吴梦雪，李永乐，周昱，等. 悬索桥超高桥塔的刚度和风致响应 [J]. 桥梁建设，2012，42(4)：14-20.

(WU Mengxue，LI Yongle，ZHOU Yu，et al. Stiffness and Wind-Induced Responses of Very High Towers of Suspension Bridge [J]. Bridge Construction，2012，42(4)：14-20. in Chinese)

[6]车鑫，李加武，高斐，等. 斜风作用下桥塔自立状态下风洞试验及抖振性能分析 [J]. 公路交通科技，2012，29(10)：84-87.

(CHE Xin，LI Jiawu，GAO Fei，et al. Wind Tunnel Test and Analysis of Buffeting Performance of Free-Standing Pylon of Cable-Stayed Bridge under Skew Wind [J]. Journal of Highway and Transportation Research and Development，2012，29(10)：84-87. in Chinese)

[7]马婷婷，葛耀君，赵林. 大跨度斜拉桥施工阶段抗风性能变化规律 [J]. 振动与冲击，2013，32(12)：100-104.

(MA Tingting，GE Yaojun，ZHAO Lin. Wind-Resistant Behavior of a Long Span Cable-Stayed Bridge during Construction [J]. Journal of Vibration and Shock，2013，32(12)：100-104. in Chinese)

[8]朱乐东，张宏杰，张海. 钢桥塔涡振气动控制措施研究 [J]. 振动工程学报，2011，24(6)：585-589.

(ZHU Ledong，ZHANG Hongjie，ZHANG Hai. Aerodynamics Mitigation Measures for Vortex-Induced Vibration of Steel Tower [J]. Journal of Vibration Engineering，2011，24(6)：585-589. in Chinese)

[9]竹剡锋，禹见达，李彬， 等. 湖区桥塔塔顶表面风压的数值模拟 [J]. 自然灾害学报，2015，24(4)：233-239.

(ZHU Yanfeng，YU Jianda，LI Bin，et al. Numerical Simulation of Wind Pressure on Bridge Tower Top Surface in Lake District [J]. Journal of Natural Disasters，2015，24(4)：233-239. in Chinese)

[10]GE Y J，XIANG H F. Recent Development of Bridge Aerodynamics in China [J]. Journal of Wind Engineering and Industrial Aerodynamics，2008，96(6):736-768.

[11]禹见达，李彬，竹剡锋. 洞庭湖大桥桥塔塔顶风场与风压特性试验研究 [J]. 湖南科技大学学报：自然科学版，2014，29(3)：49-52.

(YU Jianda，LI Bin，ZHU Yanfeng. Investigation into the Characteristics of Wind and Wind Pressure of the Tower Top of Dongting Lake Bridge [J]. Journal of Hunan University of Science & Technology:Natural Science Edition，2014，29(3)：49-52. in Chinese)

[12]李胜利，张通，陈淮，等. 门型桥塔驰振气动干扰效应数值模拟 [J]. 中国铁道科学，2012，33(1)：27-34.

(LI Shengli，ZHANG Tong，CHEN Huai，et al. Numerical Simulation on the Galloping Performance of Portal Type Bridge Tower Considering the Aerodynamic Interference Effect [J]. China Railway Science，2012，33(1)：27-34. in Chinese)

[13]李永乐，刘多特，李小波，等. 独柱式变截面倾斜桥塔气动特性风洞试验研究 [J]. 实验流体力学，2013，27(5)：38-43.

(LI Yongle，LIU Duote，LI Xiaobo，et al. Wind Tunnel Test on Aerodynamic Characteristics of Inclined Single-Column Pylons with Variable Cross Section [J]. Journal of Experiments in Fluid Mechanics，2013，27(5)：38-43. in Chinese)

[14]陶齐宇，李永乐，张明金， 等. 斜拉桥H形桥塔气动力系数风洞试验研究 [J]. 武汉理工大学学报，2009，31(13)：64-68.

(TAO Qiyu，LI Yongle，ZHANG Mingjin，et al. Measurement for Aerodynamic Coefficients of H-Shape Pylon of Cable-Stayed Bridges by Wind Tunnel Test [J]. Journal of Wuhan University of Technology，2009，31(13)：64-68. in Chinese)

[15]MASANORI Hayashi, AKIRA Sakurai, YUJI Ohya. Wake Interference of a Row of Normal Flat Plates Arranged Side by Side in a Uniform Flow[J]. Journal of Fluid Mechanics, 1986，164(1)：1-25.

[16]YUN Shun C, LIU Jung H. Wake Flow behind Two Side-by-Side Square Cylinders[J]. International Journal of Heat and Fluid Flow，2011，32(1)：41-51.

[17]MELBOURNE W，SHARP D. Effects of Upwind Buildings on the Response of Tall Buildings [C]//Hong Kong：Proceedings Regional Conference on Tall Buildings，1976：171-191.

[18]LAM K M，LEUNG M Y H，ZHAO J G. Interference Effects on Wind Loading of a Row of Closely Spaced Tall Buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics，2008，96(5)：562-583.

[19]SURRY D，MALLAIS W. Adverse Local Wind Loads Induced by Adjacent Building [J]. ASCE Journal of Structural Engineering,1983，109(3)：816-820.

[20]KWORK K C S. Aerodynamics of Tall Buildings：a State of the Art in Wind Engineering [C]//Proceedings of the 9th International Conference on Wind Engineering.New Delhi：International Association for Wind Engineering,1995:180-204.

[21]KHANDURI A C，STATHOPOULOS T，BÉDARD C. Wind-Induced Interference Effects on Buildings—a Review of the State-of-the Art [J]. Engineering Structures，1998，20(7)：617-630.

[22]中华人民共和国交通部. JTG/T D60-01-2004 公路桥梁抗风设计规范[S]. 北京：人民交通出版社，2004.

(Ministry of Communications of the People’s Republic of China. JTG/T D60-01-2004 Wind-Resistant Design Specification for Highway Bridges [S]. Beijing：China Communication Press，2004. in Chinese)