基于优化蚁群算法的钢轨轮廓识别
2017-04-09旷文珍李积英
旷文珍,常 峰,许 丽,李积英
(1.兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070;2.兰州交通大学 光电技术与智能控制教育部重点实验室,甘肃 兰州 730070;3.兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
随着铁路高速化和重载化的快速发展,铁路运输的自动化程度要求也越来越高。在列车高速运行过程中,依靠司机用肉眼观察铁路障碍物劳动强度大、不可靠,且即使司机发现了障碍物也有可能来不及采取有效的措施。因此将图像识别技术应用到铁路障碍物识别中,一方面可以对障碍物进行无间断的实时监测,减少行车事故的发生;另一方面可以减小司机的劳动强度,减少路轨的维护工作,提高经济效益[1-2]。
对障碍物进行识别时,首先需要识别出2条钢轨的边缘,沿着2条钢轨边缘外侧向两侧延伸一定的识别范围,从而建立有效的检测窗,再识别窗内的障碍物。因此对铁路钢轨边缘的有效识别是检测障碍物的前提条件[3]。蚁群算法是根据真实的群体蚂蚁寻找食物的这种行为得到了启发而提出来的算法,被广泛地应用于边缘识别[4-6]。该算法具有自组织性、并行性、正反馈性和鲁棒性优良的特性,但也存在搜索时间过长、在执行过程中容易出现停滞现象,当问题规模较大时还存在陷入局部最优的可能性等缺陷。
本文根据铁路钢轨边缘识别的特点,提出基于图像边缘特征的蚁群优化算法,在蚁群初始化、搜索过程、搜索步长、信息素更新策略等方面都作了针对性的优化,很好地解决了传统蚁群算法在初始化时搜索速度慢、易陷入局部最优解、图像复杂时处理速度慢等问题。
1 基于传统蚁群算法的钢轨边缘识别
将需要识别的钢轨图像抽象为1幅由像素点组成的二维无向图,将蚂蚁随机放置在这个二维的无向图中,每个蚂蚁在其8邻域内的像素点上随机移动,如图1所示(图中i和j分别为蚂蚁所在位置的横向和纵向坐标),同时会使经过路径上的信息素强度发生变化,经过多次循环迭代后让大多数蚂蚁聚集到图像的边缘上;完成最初设置的迭代次数之后,最后根据设定的阈值判定边缘点,从而最终完成钢轨边缘的识别。具体识别过程[7-8]如下。
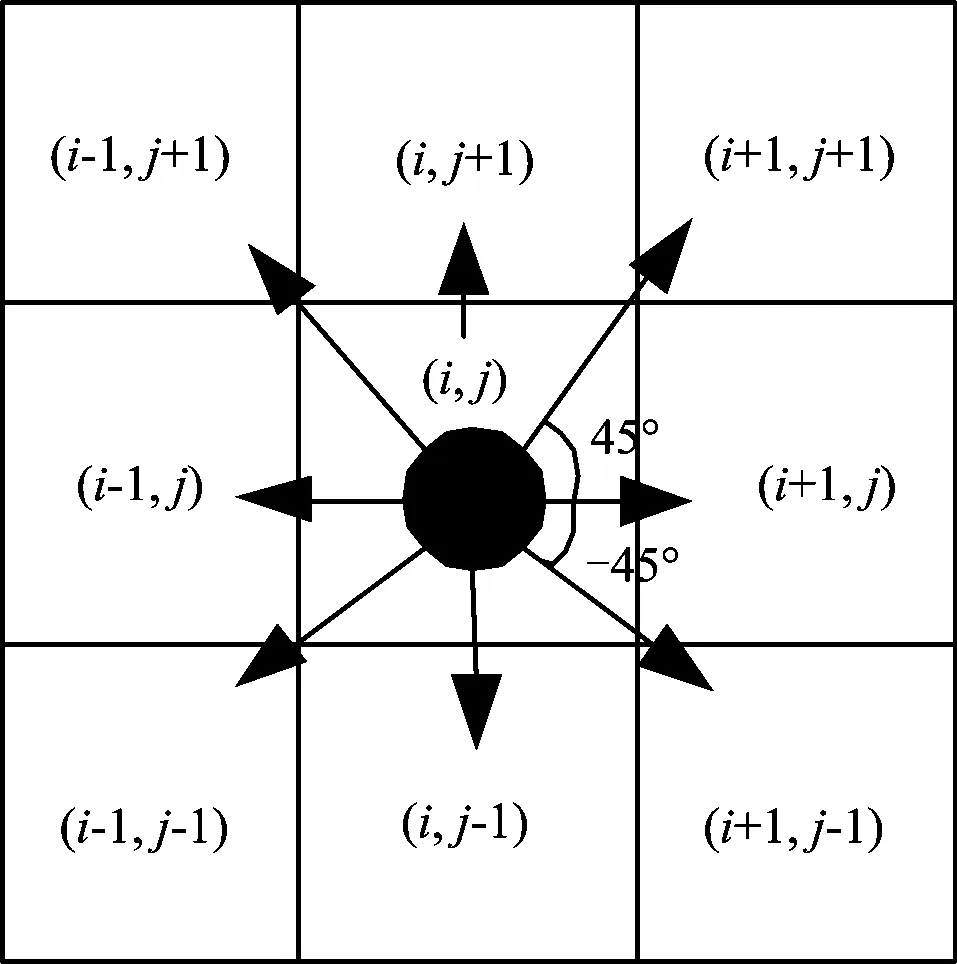
图1 3×3邻域内蚂蚁的随机移动示意图
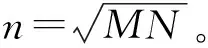


(1)
式中:τ(i,j)(t)为蚂蚁k在像素点(i,j)的信息素;α为信息素浓度影响因子;β为启发式引导函数影响因子。
从式(1)可以看出,在每一次迭代运算中,蚂蚁从像素点(i0,j0)到像素点(i,j)的转移概率都要受到α和β这2个影响因子的作用,因此α和β的取值要求适当。若α=0,信息素对蚂蚁的路径选择不起作用;若β=0,此时只有信息素浓度起作用,该算法就会迅速找到非最优解,这对寻找钢轨边缘像素点非常不利。
步骤4:信息素更新。当每只蚂蚁从钢轨图像的一个像素点移动到另一个像素点时,系统会对信息素进行局部更新;当所有蚂蚁遍历完所有像素点时,系统会对信息素进行全局更新。这样避免因残留的信息素过大而淹没启发式信息。每只蚂蚁从像素点(i0,j0)移动到(i,j)处,即在下一时段均找到了可行解时,该路径上的信息素发生局部更新,更新方程如下。
τ(i0,j0),(i,j)(t+1)=(1-ρ1)τ(i0,j0),(i,j)(t)+
(2)
其中,

当n只蚂蚁都完成迭代运算后,在走过的路径上会产生全局信息素更新,更新方程如下。
τ(i0,j0),(i,j)(t+1)=(1-ρ2)τ(i0,j0),(i,j)(t)+ρ2τ0
(3)
式中:ρ2为全局信息素挥发率,ρ2∈(0,1);τ0为信息素初始值。
若ρ1和ρ2的取值过小,蚂蚁对信息素的敏感度增强,会选择其他蚂蚁曾经走过的路径,导致全局搜索能力下降;若取值过大,虽然增大了蚂蚁的全局搜索能力,但是同时也加大了搜索的时间。
步骤5:终止条件。如果蚂蚁没有遍历完所给钢轨图像的像素点,即当前迭代次数d<预先设置的迭代次数D时,转至步骤2;否则继续步骤6。其中迭代次数D是根据图像的大小和复杂程度预先设置的,钢轨图像越大、越复杂,迭代次数则越多。
步骤6:选择边缘点。当所有蚂蚁完成预先设置的D次迭代后,设定信息素的阈值T与各信息素强度E进行比较,然后确定出边缘点,对图像做细化处理后便可以得到整个钢轨图像的边缘。确定边缘点像素的方程如下。
(4)
式中:当取值为1时,表示像素点(i,j)为边缘像素点;当取值为0时,表示像素点(i,j)为非边缘像素点。
2 基于优化蚁群优化算法的钢轨边缘识别
2.1 初始化过程的优化
采用传统的基于蚁群算法的钢轨边缘识别方法时,因为初始化时是将蚂蚁随机分布,故会导致搜索初期蚂蚁在非边缘图像区域进行大量的、无关的运算。为了解决传统蚁群算法在搜索初期搜索效率低、停滞和收敛速度慢等缺点,在初始化时应用一维Logistic混沌映射产生混沌序列[9],利用混沌向量具有较好的遍历性和随机性的特点对蚁群进行初始化分布,提高搜索效率。具体方法如下。
首先,将蚂蚁随机分布在钢轨图像的各个像素点上,则蚂蚁k初始坐标映射的混沌变量xk(t)为
(5)
式中:a和b分别为钢轨图像坐标的最小值和最大值。
其次,在生成混沌变量后,对混沌变量的每个分量进行一维Logistic混沌操作,即
xk+1(t+1)=μ(t)xk(t)[1-xk(t)]
k=1,2,…,n
(6)
式中:μ(t)为控制参数, 本文取μ(t)=4, 且xk(t)∉{0,0.25,0.5,0.75,1}时系统处于完全混沌状态[10]。
按照式(6)分别赋值给函数的每一维自变量,利用全排列理论,将每个混沌变量对应1条搜索路径,并从中选择1条较优的路径,使得路径上留下的初始信息素值各不相同,从而提高搜索的效率。
最后,将混沌变量的每个分量映射到钢轨图像的遍历空间里,即
Xk(t)=a+xk(t)(b-a)Xk(t)∈[a,b]
(7)
式中:Xk(t)为钢轨图像空间中蚂蚁k在t时刻的位置坐标。
通过式(7)可为每只蚂蚁生成1个随机位置,然后应用式(1)实现对路径的选择,这样蚂蚁在初始路径选择时就会分布在整个钢轨图像中,从而有效避免陷入局部最优解。
2.2 搜索过程的优化
选择像素点(i,j)的8个邻域4个方向上邻域内的灰度梯度变化最大值ΔI(i,j)作为像素点(i,j)的灰度变化值。
ΔI(i,j)=max{|I(i,j+1)-I(i,j-1)|,
|I(i-1,j+1)-I(i+1,j-1)|, |I(i-1,j)-I(i+1,j)|, |I(i-1,j-1)-I(i+1,j+1)|}
(8)
式中:I(i,j)为像素点(i,j)处的灰度值。
由式(8)可见,如果像素点(i,j)在边缘处, 则ΔI(i,j)的值比较大。
在初始阶段,蚁群在搜索范围内采用随机搜索策略进行单个边缘像素点识别。蚂蚁从像素点(i-1,j-1)移动到像素点(i,j),且每次移动1个步长,则根据式(9)判断边缘像素点灰度梯度的变化值。
|ΔI(i,j)-ΔI(i-1,j-1)|≥Te
(9)

蚂蚁每次移动到1个像素点后,识别像素点灰度梯度变化值,若满足式(9),则停止搜索,且判断该像素点是否是边缘像素点;否则,继续搜索。为了防止蚂蚁无限制地搜索下去,提高搜索效率,人工设置1个最大搜索步数为L。
蚂蚁k每走一步都要更新自己的坐标位置以及搜索方向。设定蚂蚁在纵向和横向移动的步长均为L1=(b-a)/n, 则蚂蚁k更新位置的算式为
Xk(t+1)=(X1k(t)+int[-λ,λ]L1,X2k(t)+int[-λ,λ]L1)
(10)
(11)
式中:X1k(t)和X2k(t)分别为蚂蚁k在t时刻的横、 纵坐标;θk(t+1)为蚂蚁k在t+1时刻搜索方向的角度;int[·]为取整函数;λ为步长系数;θ的取值为{0°, ±45°, ±90°,±135°,180°};(i(t),j(t))为t时刻蚂蚁的位置坐标。
识别到钢轨边缘上的某个像素点(i,j)后,以该像素点为中心,再次判断一定邻域内与该像素点灰度级数相似的像素点,并将其也定为钢轨边缘上的1个像素点,然后循环这个过程,最后将这些识别出的像素点连成1条平滑、完整的钢轨边缘线,完成对钢轨轮廓的识别;将沿钢轨边缘的像素点集合记为Ω3(i,j)。
为了分析方便,建立蚂蚁区域搜索模型如图2所示。

图2 蚂蚁区域搜索模型
从图2可以看出:将钢轨图像划分为M×N个小正方形,假设蚂蚁所在位置的像素点为(i,j),位于小正方形的中心位置,其移动方向与水平方向的夹角为θ,则直径为cd的半圆区域是蚂蚁能够感应到的范围,感应到的像素点在图中已标出,感应邻域集合记为Ω4(i,j)。
2.3 搜索步长的优化
传统的蚁群算法采用固定的搜索步长,由于有些图像中非边缘区域较多,使得算法进行了大量的无关运算,导致搜索时间变长,效率变低。为了进一步提高边缘识别效率,本文根据不同情况采用2种步长的搜索策略。
(1)如果蚂蚁k从像素点(i-1,j-1)移动到像素点(i,j),其灰度变化值不满足式(9),表明不存在边缘点,则蚂蚁k采用大步长(步长系数λ取大值λmax)搜索策略进行移动,移动到位置后,根据式(10)和式(11)更新自己的坐标位置,此时λmax的取值要合理。λmax过小,虽能够体现图像边缘识别的细节部分,但是会造成检测时间过长,识别效率低等弊端;λmax取值过大,虽然会加快边缘识别速度,但是会丢失边缘的细节。
(2)如果蚂蚁k从像素点(i-1,j-1)移动到像素点(i,j),其灰度变化值满足式(9),表明可能存在边缘点,然后根据式(12)进行判断。
|ΔI(i,j)-ΔI(i-1,j-1)|≤Ts
(i,j)∈Ω4(i,j), (i-1,j-1)∈Ω3(i,j)
(12)
式中:Ts为边缘像素点灰度值的相似阈值。
若满足式(12),表明像素点(i,j)与(i-1,j-1)相似,都是边缘像素点,此时则采用小步长(步长系数λ取小值λmin)进行边缘精确搜索,且0<λmin<1,然后根据式(12)和式 (13)更新位置,更新方程如下。
Xk(t+1)=X1k(t)+

(13)
然后应用区域搜索策略将各个边缘点连为1条完整连续的钢轨边缘。
2.4 信息素更新策略的优化
蚂蚁每移动1步发生局部信息素更新,更新方程如下。
τ(i0,j0),(i,j)(t+1)=
(14)
式中:ρ3为系数,0<ρ3<1。
本文只对局部信息素更新方程进行改进,为了防止算法陷入局部最优,将蚂蚁经过的每条路径上的信息素的浓度限定在确定范围内,在每次进行完迭代运算后保留最优解。如果不进行范围的限定,信息素浓度过小,使算法的收敛速度变慢;而信息素浓度过大,则会使算法容易陷入局部最优。改进后的信息素浓度更新方程如下。
τ(i0,j0),(i,j)(t+1)=
(15)
式中:τ0为在蚂蚁还未开始搜索的初始时刻,为了使蚂蚁能够尽快找到搜索路径而设置的信息素值;Q0为每只蚂蚁每完成1次迭代,信息素局部更新开始时的值。
3 仿真试验
3.1 性能分析试验
为了验证优化算法相对于传统算法具有求解速度快的优点,采用软件Matlab7.10.0编程,分别用测试函数Ackley函数[11]f1(x)和Griewank函数[12]f2(x)分别对传统算法和优化算法进行测试,寻找其极值,有
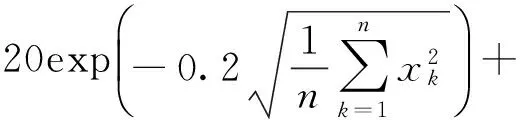
a≤xk≤b
(16)
a≤xk≤b
(17)
试验次数为10次,蚁群数量均为128个,最大迭代次数为1 000次,优化结果分别见表1和表2。

表1 Ackley函数优化结果分析

表2 Griewank函数优化结果分析
从表1和表2可以看出:较传统算法,优化算法在寻优过程中能够较快地找到最优解,求解速度快;优化算法的绝对误差和相对误差较小,准确度较好;优化算法的方差较小,稳定性较好。
3.2 有效性分析试验
为了验证优化算法的有效性,分别以采集到的(128×128)像素的直轨和弯轨钢轨图像为例,用Matlab7.10.0软件编程实现仿真,参数选择为:α=0.6,β=0.4,ρ1=0.4,ρ2=0.3,ρ3=0.2,D=2 000,T=0.7,Te=0.8,λmax=2,λmin=0.5,Ts=0.2,τ0=0.1,L=1 000,Q0=τmin=0.1,τmax=0.9。
分别应用Canny边缘检测算子、传统算法和优化算法对直轨钢轨图像边缘进行识别,结果如图3所示。
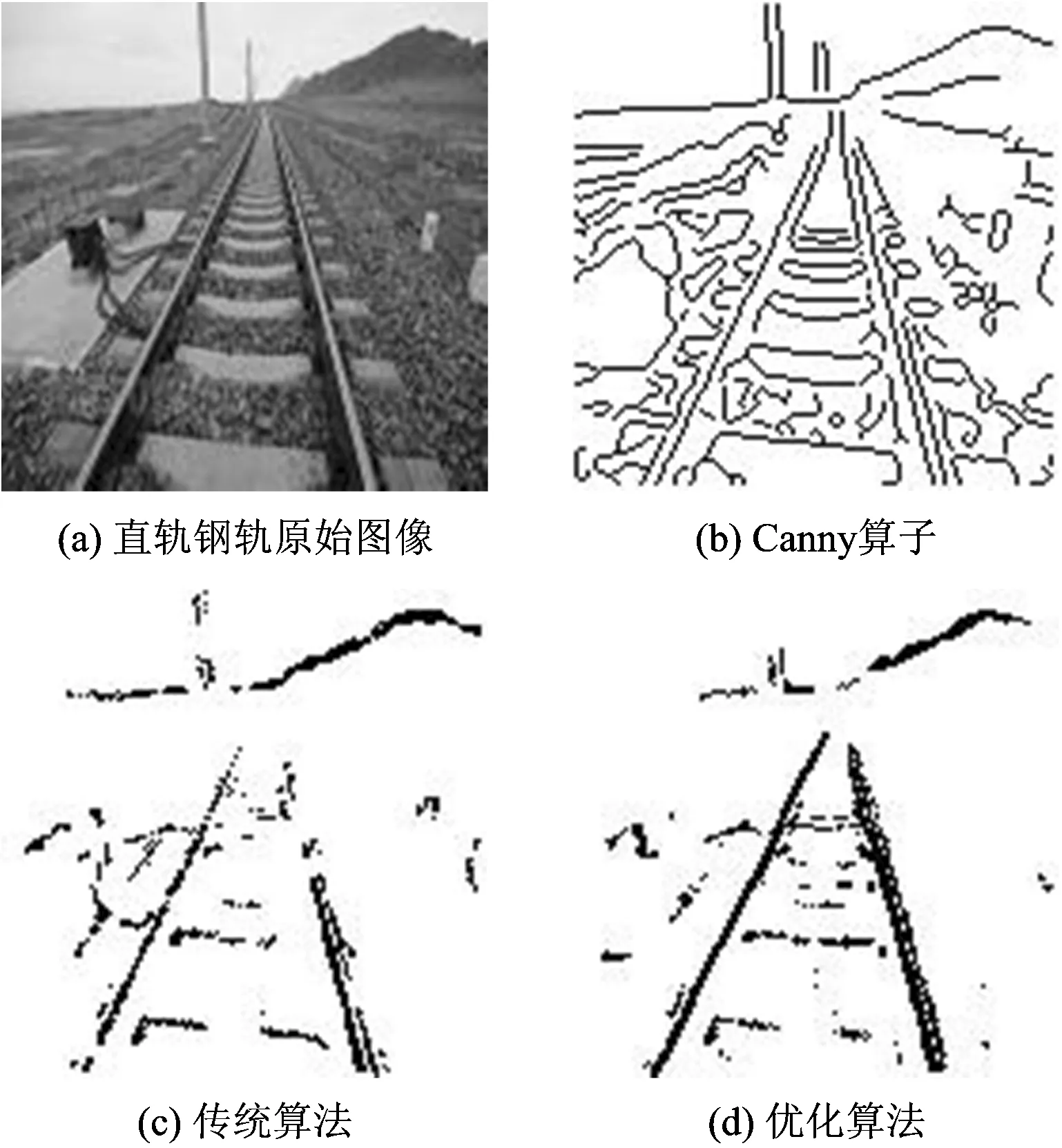
图3 直轨钢轨边缘识别
从图3可以看出:用Canny算子提取的钢轨边缘与背景没有区分开,且提取的钢轨线条较细,不清晰,不利于下一步的障碍物识别;用传统算法提取的钢轨边缘轮廓较明显,但是钢轨线条有不连续的倾向;用优化算法提取的钢轨边缘能够很好地与背景等无关区域相区分,轮廓更加清晰、粗壮和完整,能为铁路障碍物识别提供良好的钢轨轮廓,为下一步的障碍物识别提供有效的依据。
为了进一步验证优化算法的有效性和适应性,对采集的弯轨钢轨图像分别应用Canny边缘检测算子、传统算法和优化算法进行识别,结果如图4所示。

图4 弯轨钢轨边缘识别
从图4中可以看出:用Canny算子提取的钢轨边缘对细节的提取较多,有用的钢轨边缘与其他无用的过多细节部分完全混合在一起,不能进行很好的区分;用传统算法提取的钢轨边缘轮廓较Canny算子明显程度有很大的提升,但是提取的钢轨线条不光滑,小部分线条还存在不连续的问题;用优化算法提取的弯轨钢轨轮廓光滑、粗壮和连续,能够滤除大部分无关细节部分,有较好的适应性,能很好的应用于铁路路轨障碍物识别。
分别应用传统算法和优化算法对直轨钢轨图像和弯轨钢轨图像进行边缘提取,进行100次试验,各算法的平均识别时间见表3。
从表3可以看出:优化算法在识别时间上优于传统算法,这是因为优化算法在识别边缘点时,采用大步长的搜索机制,识别到边缘点后,再应用区域搜索策略缩小搜索范围,加快了搜索过程,减少了识别时间。

表3 传统和优化算法识别直轨和弯轨钢轨图像的平均识别时间比较 s
4 结 语
在钢轨识别中,对传统的蚁群算法在初始化过程、搜索过程、搜索步长、信息素更新策略4个方面进行优化后,能使识别出的钢轨轮廓更加光滑、粗壮和连续,并且能有效提高识别效率。但是还是存在一些不足,不能将钢轨和钢轨的阴影部分进行很好的区分,有待改进和完善。
[1]史红梅,柴华,王尧,等. 基于目标识别与跟踪的嵌入式铁路异物侵限检测算法研究[J].铁道学报, 2015,37(7):58-65.
(SHI Hongmei,CHAI Hua,WANG Yao,et al. Study on Railway Embedded Detection Algorithm for Railway Intrusion Based on Object Recognition and Tracking [J].Journal of the China Railway Society,2015,37(7):58-65. in Chinese)
[2]王前选,梁习锋,刘应龙,等. 缓变异物入侵铁路线路视觉检测方法[J].中国铁道科学, 2014,35(3):137-143.
(WANG Qianxuan,LIANG Xifeng,LIU Yinglong,et al.Visual Detection Method for the Invasion of Slowly Changing Foreign Matters to Railway Lines[J]. China Railway Science,2014,35(3):137-143. in Chinese)
[3]于革,贾利民,秦勇,等. 视频监控铁路限界内逗留物体的检测方法[J].中国铁道科学, 2013,34(4):105-109.
(YU Ge,JIA Limin,QIN Yong,et al. Method for Detecting Loitering Objects within Railway Clearance by Video Surveillance[J]. China Railway Science,2013,34(4):105-109. in Chinese)
[4]MARCO D, LUCA Maria Gambardella. Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem[J]. IEEE Transactions on Evolutionary Computation,1997,1(1): 53-66.
[5]BATERINA A,OPPUS C. Image Edge Detection Using Ant Colony Optimization[J]. Wseas Transactions on Signal Processing,2010,6(2):58-67.
[6]李积英,党建武. 量子蚁群模糊聚类算法在图像分割中的应用[J].光电工程, 2013, 40(1): 126-131.
(LI Jiying, DANG Jianwu. Image Segmentation Based on Quantum Ant Colony Fuzzy Clustering Algorithm [J]. Opto-Electronic Engineering,2013,40(1):126-131.in Chinese)
[7]GANESHKUMAR P,RANI C,DEVARAJ D. Hybrid Ant Bee Algorithm for Fuzzy Expert System Based Sample Classification[J]. IEEE Transactions on Computational Biology and Bioinformatics, 2014, 11(2): 347-360.
[8]HO S L, YANG Shiyou, BAI Yanan. An Ant Colony Algorithm for Both Robust and Global Optimizations of Inverse Problems[J]. IEEE Transactions on Magnetics,2013,49(5):2077-2080.
[9]MANDAL M,BANIK G,CHATTOPADHYAY D,et al. An Image Encryption Process Based on Chaotic Logistic Map [J]. IETE Technical Review,2012,29(5):395-404.
[10]耿艳香, 孙云山, 谢靖鹏. 混沌蚁群算法在图像边缘检测中的应用[J]. 计算机工程及应用, 2015,51(2):194-197.
(GENG Yanxiang, SUN Yunshan, XIE Jingpeng. Research on Chaotic Ant Colony Algorithm in Image Edge Detection[J]. Computer Engineering and Applications,2015,51(2):194-197. in Chinese)
[11]SYLVIE Le Hégarat, ABDELAZIZ Kallel, XAVIER Descombes. Ant Colony Optimization for Image Regularization Based on a Nonstationary Markov Modeling[J]. IEEE Transactions on Image Processing, 2007, 16(3): 865-878.
[12]CHEN S M, CHIEN C Y. A New Method for Solving the Traveling Salesman Problem Based on the Genetic Simulated Annealing Ant Colony System with Particle Swarm Optimization Techniques[C] //2010 International Conference on Machine Learning and Cybernetics. Qingdao:IEEE,2010: 2477-2482.
