底坎对减缓采沙河床桥墩冲刷的效果及机理研究
2017-04-09齐梅兰杨熠琳郐艳荣
齐梅兰,杨熠琳,郐艳荣
(1.北京交通大学 土木建筑工程学院,北京 100044;2.北京交通大学 结构风工程城市风环境北京市重点实验室,北京 100044)
河流桥下河床的冲刷(常称为桥墩冲刷)会影响铁路桥梁的动力特性[1-2],甚至导致桥梁垮塌。尤其是近些年来,受在河道内大规模采沙的影响,既有桥梁的桥墩冲刷变得更加复杂、严重且不可逆[3-4]。因此,在预估最大冲刷深度[5]的基础上,采取适当的防护措施是十分必要的。
桥墩冲刷通常按一般冲刷和局部冲刷之和来计。桥墩冲刷的防护在自然河流上多以防护墩周局部冲刷为主,称为局部防护。其原理主要是提高局部河床抵抗桥墩周围马蹄涡流强动力[6-7]的能力,如工程上常用的墩周抛石防护措施,即是以大尺度石块的重力作用抵抗水流的动力作用。为避免因抛石设计不当而引起“再冲刷”[8-9],很多文献提出了抛石防护的优化设计[10-12]。在有人为大规模采沙的河流上,由采沙河床后续演变引起的桥墩冲刷以一般冲刷为主,当桥下河床发生大范围冲刷时,仅对桥墩进行局部防护将不能保证大桥的安全。根据本文作者的研究,在动床冲刷条件下桥址上游近距离采沙时采沙河床将向下游演变,在清水冲刷条件下桥址下游采沙时采沙河床将向上游演变,又称溯源冲刷[13]。采沙河床的这2种演变都以一般冲刷增大为主。由于采沙位置和采沙量的任意性以及其所诱发的桥墩冲刷特点,决定了桥墩冲刷防护应以全断面防护方式为宜,如底坎拦沙防护。但目前相关研究较少,Grimaldi等通过对墩下游设置顶部与床面等高的底坎试验得出结论,底坎距墩越近,减少冲刷的效果越好[14]。Tafarojnoruz等认为底坎最多仅能减少桥墩冲刷20%[15]。已有的研究对底坎减冲效果的认识还不够全面。因此,充分认识底坎设计尺度与水流及输沙的变化机理,进而深入研究底坎减冲效果的最优设计是十分必要的。
本文针对采沙影响下的桥墩冲刷问题,通过水力学分析和水槽试验,研究底坎设置对桥墩冲刷的减冲效率,并运用粒子图像采集技术对试验中的不同底坎尺度下的水流紊动结构进行分析,探讨底坎影响水流紊动及减缓冲刷的机理。
1 底坎高度与水流强度的变化关系
图1为底坎上下游水流变化示意图,其中水流按一维流考虑。设水的恒定来流流量为Q,无底坎时为均匀流,其深为h0,流速为v0,水流弗劳德数为Fr0,水面(图中虚线)与床面相平行。设置与河道等宽、高度为δ的底坎后,对水流产生作用力FD,形成上游水面壅高增量Δh,水深增大至h(h=h0+Δh),底坎下游水流逐渐恢复至均匀流状态。取底坎上游断面1与处于均匀流区的下游断面0间的流体作为隔离体,研究其运动。设v1和P1分别为断面1的流速和压力,P0为断面0的压力。2个断面间的流体运动满足动量方程
P1-P0-FD=ρQ(v0-v1)
(1)
式中:ρ为水的密度,取1 000 kg·m-3。
设P1和P0服从静压分布规律,则
(2)
(3)
式中:g为重力加速度,取9.8 m·s-2。
FD按绕流阻力考虑,即
(4)
式中:Cd为绕流阻力系数。
根据连续方程,可知流速v1与流速v0的关系满足
v1=v0h0/(h0+Δh)=Q/(h0+Δh)
(5)
断面1和均匀流的弗劳德数Fr1和Fr0分别表示为
Fr0=v0/(gh0)1/2
(6)
Fr1=v1/(gh1)1/2
(7)
将式(2)—式(5)代入式(1),并结合式(6)—式(7),经整理得
(8)
通过式(8)的隐式解可知,δ增大将引起Δh增加,从而上游水流强度Fr1将减小。根据水沙运动理论,水流的强度减小则输沙能力降低,可达到减弱底坎上游的床面冲刷。但从图1可见,底坎的δ增高时其下游局部水面比降也增大。这将增加底坎下游根部的冲刷,不利于底坎的稳定,同时底坎上游的根部也会因高坎形成涡流冲刷[16]。因此,底坎的高度需要合理控制。
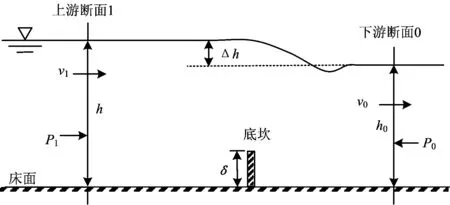
图1 底坎上、下游水流变化示意图
2 试验设计
根据式(8)和冲刷原理分析,为达到减少桥墩冲刷的最佳效果,底坎的高度需要优化,这也是本试验的目的。为了研究底坎的减冲效果,试验观测采沙河床无底坎和设置不同尺寸底坎条件下桥墩的冲刷情况。为分析底坎减冲与水流紊动的作用机制,测量了水流紊动结构的变化。
2.1 水槽试验设计
试验在可调坡的玻璃钢水槽中进行,水槽长6 m、宽0.25 m、高0.22 m。由变频泵供水循环,用电磁流量计控制流量,试验布置如图2所示。水槽底部铺设0.08 m厚、中值粒径d50为0.6 mm的石英沙。将直径D为0.04 m的圆柱墩直立布置于水槽中部观测段,底部埋于可冲沙层中。底坎设置在桥址下游,与墩柱间距为L,其作用在于,既能阻断下游采沙河床溯源冲刷的影响,也能减缓上游采沙河床下移演变的影响,促使泥沙在桥址落淤。
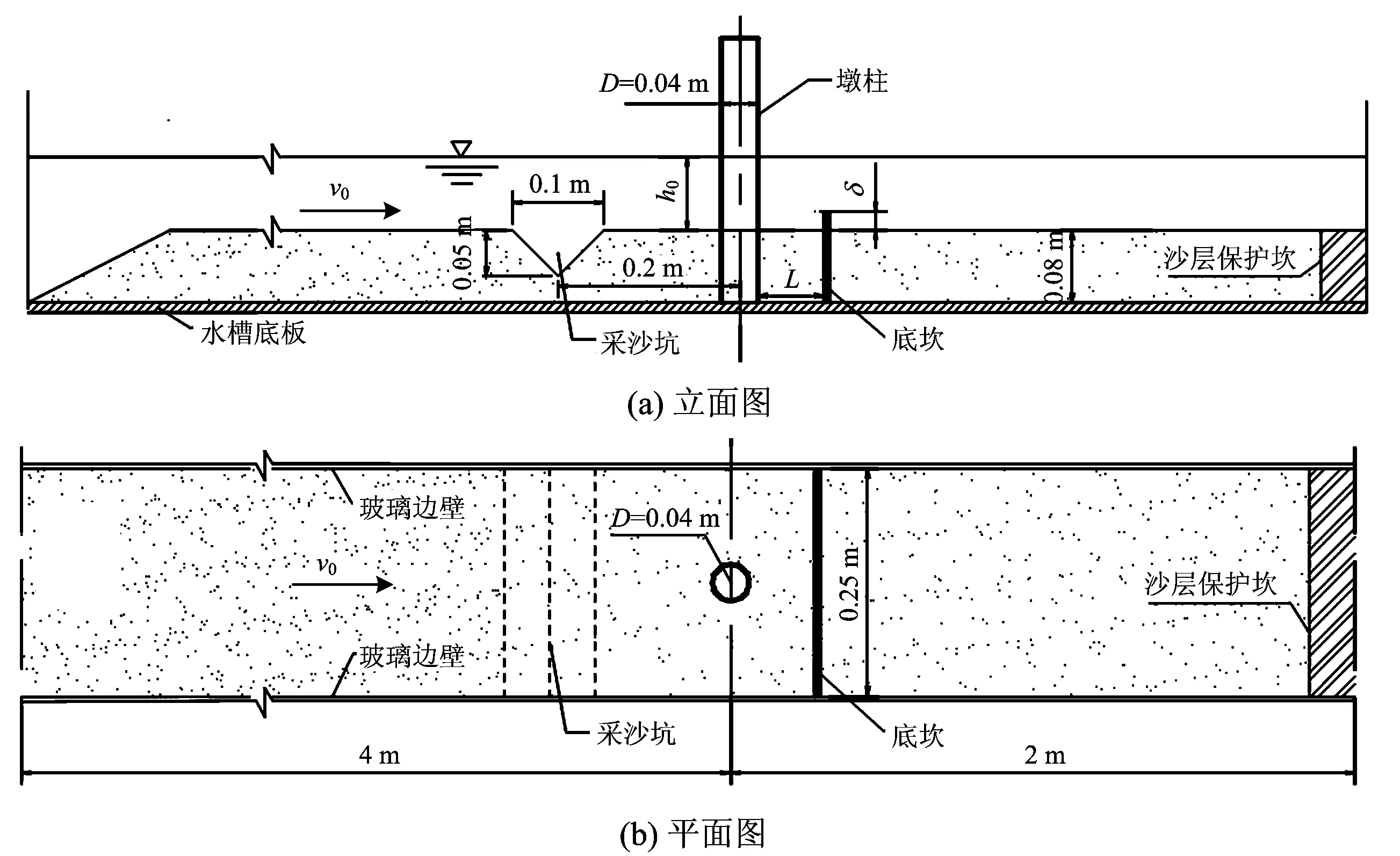
图2 试验布置图
设采沙区域与水槽同宽、纵剖面呈等腰三角形坑状,布置于墩柱上游,坑中心距墩柱0.2 m。由于下游采沙河床的溯源冲刷可被底坎阻断,因此本试验不考虑溯源冲刷的影响。试验过程中,用无干扰式地形仪实时自动采集墩柱周围沙床面高程,用无接触水位计自动记录水位,用ADV三维流速仪进行流速监测。用二维高频粒子图像采集系统观测冲刷初期底坎上游区域中心纵剖面的瞬时水流紊动特性。该系统由1 280×1 024像素的高速摄像机、功率为2 W的连续激光器、透镜系统及数据计算软件组成,测量时在水流中施加示踪粒子。
2.2 试验方案
根据采沙河床演变性质,试验分清水冲刷(v0

表1 试验方案
3 底坎减轻桥墩冲刷的效果分析
当D/d50≥50,冲刷与粒径无关[13],影响桥墩冲刷的参数主要有水流的Fr0、底坎高度δ和底坎距桥墩的距离L。用减冲效率η定量衡量底坎减轻桥墩冲刷的效果,其计算式为
η=(hs0-hs)/hs0
(9)
式中:hs0和hs分别为无防护和设坎防护后的最大冲刷深度。
下面主要分析墩前和墩侧这些最不利位置的减冲效率。
3.1 清水冲刷
在清水冲刷条件下设置底坎,主要是防护桥址下游采沙河床可能发生的溯源冲刷,同时也具有减缓墩周局部冲刷的作用。
图3给出了设置不同δ和L底坎条件下的减冲效率。由图3可见:墩周减冲效率随δ和L的改变有明显不同;各条曲线中η均有1个极大值,称为最大减冲效率ηmax(ηmax是底坎相对高度δ/h和相对距离L/D的函数),随着δ/h的增加,ηmax对应的L/D值越大;在墩前最大冲深处,当δ/h=1/3,L/D=1.5时,ηmax=29.6%;在墩侧最大冲深处,当δ/h=1/3,L/D=1.0时,ηmax=32.0%;设置同样底坎情况下,墩侧的ηmax值均大于墩前的。

图3 清水冲刷条件下底坎的减冲效率
3.2 动床冲刷
图4和图5分别给出了水流强度为Fr0=0.45和Fr0=0.49时,即动床冲刷条件下底坎的减冲效率。从图4和图5可见,与最大减冲效率ηmax对应的底坎相对高度均为δ/h=1/5,较清水冲刷条件下的δ/h偏小。动床冲刷条件下,底坎增高将使其上游根部发生局部冲刷[16],因而降低对桥墩的减冲效率;与ηmax相应的底坎相对距离L/D=1.0也较清水冲刷条件下的小;当Fr0=0.45和Fr0=0.49时,墩前最大减冲效率ηmax分别为21.3%和20.0%,墩侧最大减冲效率ηmax分别为33.3%和ηmax=28.3%。
综合分析上述试验可知,最大减冲效率ηmax随Fr0增大而减小,且与底坎设置高度及坎与墩间的距离关系显著。通过本试验对最佳底坎设置的研究获得的最大减冲效率ηmax均大于文献[14]所述的20%。

图4 动床冲刷条件下底坎的减冲效率(Fr0=0.45)

图5 动床冲刷条件下底坎的减冲效率(Fr0=0.49)
4 底坎对上游水流紊动特性及输沙率的影响
式(8)表明底坎的设置将降低水流强度Fr。下面进一步从输沙的内部机理探讨设置底坎引起的上游水流紊动特性及输沙率的变化。下面进行3种水流条件、无底坎和设置减冲效率最大底坎情况下流场及输沙率的观测分析。
4.1 紊流场的特性
通过对2 s时间内拍摄的1 000帧瞬态流场图像进行数字转换和紊动场的统计分析,得到墩前垂向二维时均紊动量(包括湍动能、涡量和切应力)的分布。Fr0=0.28时无底坎和有底坎的紊动量分布如图6和图7所示,Fr0=0.45时无底坎和有底坎的紊动量分布如图8和图9所示,图中x为距上游桥墩柱面的水平距离,z为距床面的距离。
比较图6和图7可知:设置减冲效率最大的底坎后,墩前紊流场的湍动能、涡量和切应力分布明显减弱。再比较图8和图9,也有相应的变化,但变化的量差较小。表明设置底坎的最大减冲效率ηmax随Fr0的增大而减小,与水流紊动强度随Fr0的变化呈正相关关系。
4.2 紊动量的近床面分布
冲刷是床面上泥沙受水流作用而发生运动的结果,因此,分析底坎对近床面层水流紊动的影响更有意义。试验测得的床面层紊动能和切应力的变化如图10(Fr0=0.28)和图11(Fr0=0.45)所示。

图6 无底坎时紊动量分布(Fr0=0.28)
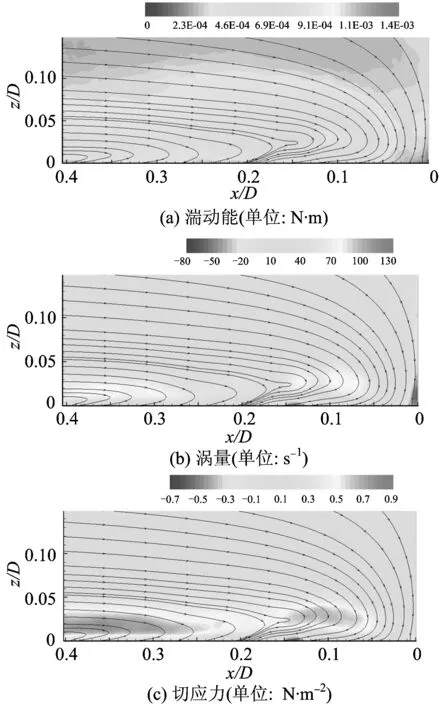
图7有底坎时紊动量分布(δ/h=1/3,L/D=1.5,Fr0=0.28)
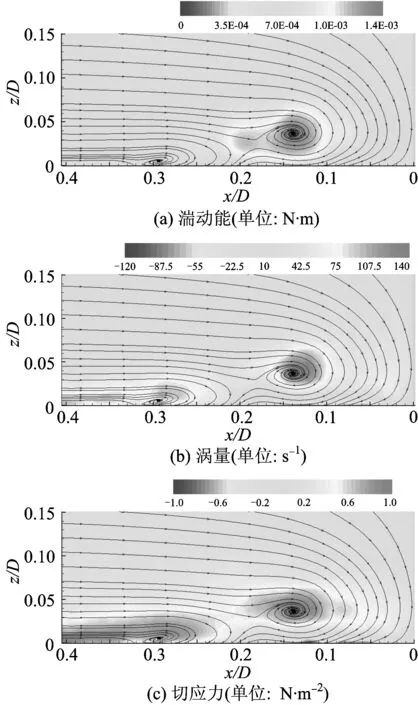
图8 无底坎时紊动量分布(Fr0=0.45)
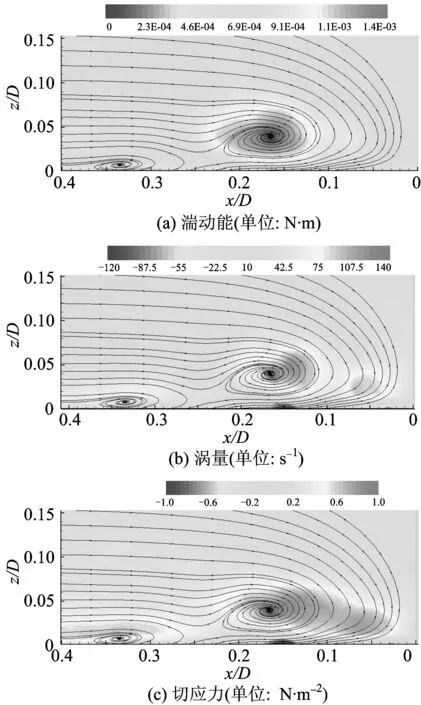
图9有底坎紊动量分布(δ/h=1/5,L/D=1.0,Fr0=0.45)

图10 底部紊动量分布(Fr0=0.28)

图11 底部紊动量分布(Fr0=0.45)
由图10和图11可见:2种水流条件下,设底坎后床面层的紊动能均明显降低;床面层的切应力由于具有方向性,其值有正有负,当切应力的绝对值|τ|与泥沙起动的临界值τc之比|τ|/τc>1时,床面泥沙发生运动,床面被冲刷。对于本文试验用的泥沙颗粒,τc=0.33 Pa,可见无底坎时|τ|/τc>1的分布范围较大,有底坎后其范围明显减小。设无底坎时的底部切应力为τ1,有底坎时为τ2,则τ1与τ2曲线包络的面积即为|τ1-τ2|在墩前区域减小量的总和,设为ΔSτ。设τ1与τ=0间包络面积为Sτ1,计算得到,图10(b)中ΔSτ/Sτ1=72.94%,图11(b)中ΔSτ/Sτ1=42.72%,表明水流弗劳德数Fr0越大,底坎对减小床面层水流切应力作用的范围越小,减冲效率越低。
4.3 底坎对输沙率的影响
设在Δt时间内桥墩冲刷深度为Δhs,则Δhs/Δt表示冲刷速率。图12给出了3种水流条件下冲刷速率的时变过程。由图12可见:设置底坎(减冲效率最大方案)后的冲刷速率与无坎时明显不同,设坎后冲刷速率的峰值减幅随Fr0的增大而减小,与减冲效率随Fr0的变化趋势相同。根据床面泥沙守恒方程(10)可知:单宽输沙率与冲刷速率成正比,故其也随Fr0的增大而减小。由此可见,底坎减冲的作用是通过减弱水流对床面泥沙的动力作用和降低水流的输沙率实现的。
(1-λ)Δhs/Δt=-Δqt/Δx
(10)
式中:λ为床沙孔隙率;qt为单宽输沙率;Δx为沿水流方向的空间差分步长。
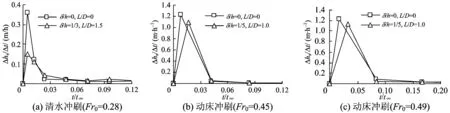
图12 不同水流条件下墩前的冲刷速率
5 结 论
(1)在桥址下游河床上沿河宽方向设置底坎,可减小桥址上游采沙河床推移演变对桥墩冲刷的影响,同时可阻断底坎下游采沙河床溯源演变对桥墩冲刷的威胁。
(2)底坎的桥墩减冲效率与底坎的高度及与桥墩的间距有关,同时随来流强度的增大而减小;清水冲刷时的最大减冲效率大于动床冲刷时,底坎相对高度及与墩间的相对距离也较动床冲刷时大。
(3)通过优化设置底坎,可降低其上游水流的时均作用和紊动作用,尤其是近床面层的水流紊动强度和切应力,进而降低水流的输沙能力,达到明显减小采沙河床对桥墩冲刷的减冲效率,最大减冲效率可达30%。
(4)采用底坎措施防护下游采沙对桥墩的冲刷时,其作用主要是阻断床面的溯源冲刷,因此,工程应用时底坎的底部基础应尽量深,并且应提前于溯源冲刷到达前设置。
[1]姚锦宝,夏禾,战家旺. 铁路桥梁基础受冲刷对桥墩自振特性的影响分析[J].中国铁道科学,2010,31(1):44-48.
(YAO Jinbao, XIA He, ZHAN Jiawang. Analysis on the Influence of the Bridge Foundation under Scouring on the Natural Vibration Characteristics of Piers[J]. China Railway Science, 2010, 31(1):44-48. in Chinese)
[2]叶爱君,张喜刚,刘伟岸. 河床冲刷深度变化对大型桩基桥梁地震反应的影响[J].土木工程学报,2007,50(3):58-62.
(YE Aijun, ZHANG Xigang, LIU Weian. Effects of Riverbed Scouring Depth on the Seismic Response of Bridges on Pile Foundations[J]. China Civil Engineering Journal, 2007,50(3):58-62. in Chinese)
[3]齐梅兰.采沙河床桥墩冲刷研究[J]. 水利学报,2005,36(7):835-839.
(QI Meilan. River Bed Scouring around Bridge Piers in River Section with Sandpits[J]. Journal of Hydraulic Engineering, 2005, 36 (7):835-839. in Chinese)
[4]LATAPIE A, CAMENEN B, RODRIGUES S, et al. Assessing Channel Response of a Long River Influenced by Human Disturbance[J]. Catena, 2014, 121(5): 1-12.
[5]KIM I, FARD M Y, CHATTOPADHYAY A. Investigation of a Bridge Pier Scour Prediction Model for Safe Design and Inspection[J]. Journal of Bridge Engineering, 2015, 20(6): 04014088.
[6]DARGAHI B. Controlling Mechanism of Local Scouring[J]. Journal of Hydraulic Engineering, 1990, 116(10):1197-1214.
[7]KIRKIL G, CONSTANTINESCU S G, ETTEMA R. Coherent Structures in the Flow Field around a Circular Cylinder with Scour Hole[J]. Journal of Hydraulic Engineering, 2008, 134(5):572-587.
[8]PAROLA A C. Stability of Riprap at Bridge Piers[J]. Journal of Hydraulic Engineering, 1993, 119(10):1080-1093.
[9]CHIEW Y M, LIM F H. Failure Behavior of Riprap Layer at Bridge Piers under Live-Bed Conditions[J]. Journal of Hydraulic Engineering, 2000, 126(1):43-55.
[10]LAUCHLAN C S, MELVILLE B W. Riprap Protection at Bridge Piers[J]. Journal of Hydraulic Engineering, 2001, 127(5): 412-418.
[11]UNGER J, HAGER W H. Riprap Failure at Circular Bridge Piers[J]. Journal of Hydraulic Engineering, 2006, 132(4): 354-362.
[12]GALAN A, SIMARRO G, SANCHEZ-SERRANO G. Nonburied Riprap Mattress Sizing for Single Piers in the Presence of Bedforms[J]. Journal of Hydraulic Engineering, 2015, 141(6):06015004.
[13]齐梅兰,刘茜,李金钊. 河床采沙挖槽的溯源冲刷影响规律[J]. 水科学进展,2016,27(6):858-866.
(QI Meilan, LIU Xi, LI Jinzhao. Retrogressive Erosion Induced by Sand Excavation on a Riverbed[J]. Advances in Water Science, 2016, 27(6):858-866. in Chinese)
[14]GRIMALDI C, GAUDIO R, CALOMINO F. Control of Scour at Bridge Piers by a Downstream Bed Sill[J]. Journal of Hydraulic Engineering, 2009, 135(1):13-21.
[15]TAFAROJNORUZ A, GAUDIO R, CALOMINO F. Evaluation of Flow-Altering Countermeasures against Bridge Pier Scour[J]. Journal of Hydraulic Engineering, 2012, 138(3):297-305.
[16]GUAN D, MELVILLE B W, FRIEDRICH H. Live-Bed Scour at Submerged Weirs[J]. Journal of Hydraulic Engineering, 2015, 141(2):04014071.
