空沟对平面纵波隔离效果的理论解答

徐 平

(郑州大学 水利与环境学院，郑州 450001)

空沟对平面纵波隔离效果的理论解答

徐 平

(郑州大学 水利与环境学院，郑州 450001)

借助复变函数的保角变换法将有限长度的空沟映射变换为单位圆，根据空沟四周完全自由的边界条件，运用波动函数展开法得到了空沟对纵波(P波)和剪切波(SV波)隔离的理论解答。引入位移比值(屏障后某点由入射波波、散射波产生的总位移与入射波单独产生的位移之比)，以入射P波为例，计算了沟宽0.4 m、沟长分别为3.0 m、4.0 m、5.0 m和6.0 m共4条空沟的位移比值，通过比较发现：随着空沟长度的增加，最佳隔振效果明显提高，区域明显增大；当空沟长度达到6.0 m时，靠近空沟的区域的隔振效果超过了70%，隔振效果比较理想。最后对比了空沟和单排柱腔列的隔振效果，结果表明：由于单排柱腔列产生波的透射和绕射，而空沟仅产生波的绕射，6.0 m长空沟的最佳隔振效果与8根半径1.0 m的单排柱腔列相当，因此在场地和施工条件都允许的前提下，宜优先考虑空沟进行隔振。

空沟；平面纵波；隔离效果；保角映射；隔振设计

随着我国城镇化的迅猛发展，各种建筑和交通设施(交通干道、地铁、高架等)都得到大量的建设，居民区、商业中心、工业区和交通干道逐渐形成一个立体的交通网，使得我们整个城市几乎每时每刻都在产生着频率高、荷载循环次数大的人工振动[1]。人工振动已经成了一种新形式的环境污染，并被列为世界七大环境公害之一。

屏障是缓解人工振动强度的主要措施，屏障一般分为连续屏障和非连续屏障两种形式[2]。目前，关于空沟和填充沟等形式的连续屏障已经进行了大量的试验和数值模拟：① 试验方面：RICHART[3]通过空沟隔振试验提出了隔振效果评价指标；ERKAN等[4]采用电动摇振器产生激振荷载，通过测试和对比加速度信号研究了空沟的隔振效果；徐平等[5]采用FWD(落锤式弯沉仪)的重锤产生冲击荷载，通过对比测试和对比竖向位移分析了空沟的隔振效果；ULGEN等[6]采用总重80 kN、偏心重10 kN的振动压路机产生激振荷载，分析了频率、土层参数和空沟尺寸等对空沟隔振效果的影响；② 在数值模拟方面：ADAM等[7]采用FEM-BEM耦合方法研究了空沟对列车荷载的隔振问题；淳庆等[8]采用ANSYS软件模拟了空沟对强夯施工的隔振问题，通过数值拟合给出了空沟隔振效果的近似公式；王晓等[9]运用ANSYS软件模拟了上海自由电子激光工程的三维空沟隔振问题。

上述研究结果表明，空沟对强夯施工、交通荷载、冲击振动等都具有比较理想的隔振效果，沟深是影响空沟隔振振效果的主要因素，而沟宽对隔振效果影响不大。连续屏障和非连续屏障等被动隔振机理可以从波动理论作出定性解释：在振源与保护建(构)筑物之间设立屏障，阻断振动波传播途径，消耗振动波携带的能量，进而达到隔振或减振的目的。但当前关于空沟隔振的研究主要集中于试验和数值模拟，而未见基于波动理论开展的研究报道。本文借助复变函数的积分变换法将有限长度的隔振沟变换为单位圆，运用波函数展开法建立空沟对平面P波和SV波隔振的理论解答，以入射平面P波为例，分析了空沟的隔振效果，最后从波的传播机理上对比了空沟与单排柱腔列屏障的隔振效果。

1 空沟对P波的散射解答

土体内传播两种弹性波：P波(传播方向和偏振方向一致)和S波(传播方向和偏振方向垂直)，而S波又可进一步分解成SH波(偏振方向水平)和SV波(偏振方向竖直)。SH波散射时只包含SH波成分，而P波和SV波会产生耦合散射，即散射波同时包含P波和SV波成分，因此关于空沟对P波和SV波隔离问题的研究思路是一致的，本文首先给出空沟对P波隔离问题的解答。

将土体视为各向同性的无限均质弹性体，不计空沟深度的影响，采用复变函数的保角变换方法[10]，引入保角变换z=ω(η)可将宽度为a、长度为b的空沟从Z平面映射为η平面内的单位圆，如图1所示。

在η平面内取η=rexp(iθ)，其中，r和θ为η点的极坐标，r和x轴的夹角为γ，如图2所示。

图2 极坐标系和直角坐标系的关系Fig.2 Relationships between polar and rectangular coordinate system

对于频率为ω的入射P波，在直角坐标系(x,y)下，其势函数可以写成

φinc=φ0exp[ikp(xcosα+ysinα)]

(1)

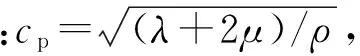
(2)

采用保角变换z=ω(η)，式(2)可进一步写成

(3)

(4a)

(4b)

采用z=ω(η)保角变换后，式(4)可进一步写成

(5a)

(5b)

在极坐标系(r,θ)下，正应力σr和剪应力τrθ的求解公式为[11-12]

(6a)

(6b)

假定空沟四周完全自由，即应力为零

(7)

将式(3)、(5)和(6)代入式(7)，经过整理可得关于待定复系数An和Bn的无穷线性方程组

(8)

上式简写成

(9)

式中：λ*=λ/μ。

将式(9)左右两端同乘以e-imθ，并对变量θ在区间[-π,π]上求积分，则得到关于待定复系数An和Bn的理论解的无穷线性方程组

(10)

(11a)

(11b)

在极坐标系(r,θ)下，径向位移ur和环向位移uθ的求解公式为[11-12]

(12a)

(12b)

将式(3)和(5)代入式12(a)和12(b)可得任意一点处由入射P波、散射P波和SV波引起的位移

(13a)

(13b)

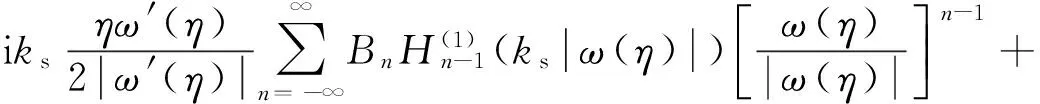
(13c)

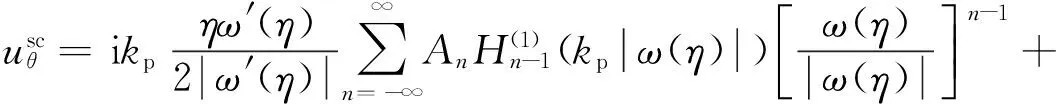
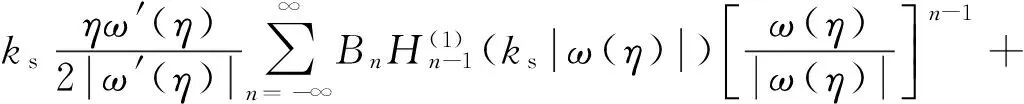
(13d)

2 空沟对SV波的散射解答

(14)

(15a)

(15b)

3 隔振效果分析

3.1 空沟隔振效果分析

入射P波和SV波的结论比较接近，限于篇幅，本文只给出入射平面P波的数值计算结果。

对于极坐标系下的任一点(rj,θj,)，uy和u0可由下式确定

(16a)

(16b)

土体内波纵和横波的波速分别取cp=160 m/s和cs=100 m/s，固有圆频率取ω=75 Hz；空沟宽度a取0.4 m，长度b分别取3.0 m、4.0 m、5.0 m和6.0 m。通过计算得到空沟后一定区域内(-10 m≤x≤10 m，0≤y≤200 m)的|uy/u0|等值线，如图3所示。

从图3可以看出，当空沟长度b由3.0 m增大到6.0 m时，相同|uy/u0|等值线所占的区域面积明显增大，以|uy/u0|≤0.6(即隔振效果≥40%)为例，区域面积分别为4 m2、400 m2、900 m2和3 400 m2；特别是当b=6.0 m时，隔振效果比较理想，空沟后y≤100 m区域的隔振效果超过了50%，y≤80 m区域的隔振效果超过了60%，y≤50 m区域的隔振效果超过了70%，空沟后近处的隔振效果好于远处。

(a) b=3.0 m

(b) b=4.0 m

(c) b=5.0 m

3.2 空沟与单排柱腔屏障隔振效果对比

作为对比，根据文献[13]，取单排柱腔组成的非连续屏障参数如下：柱腔数为8、半径为1.0 m、间距为s=3.0 m，整体宽度为23.0 m。单排柱腔和空沟的尺寸如图4所示。

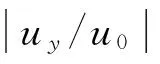
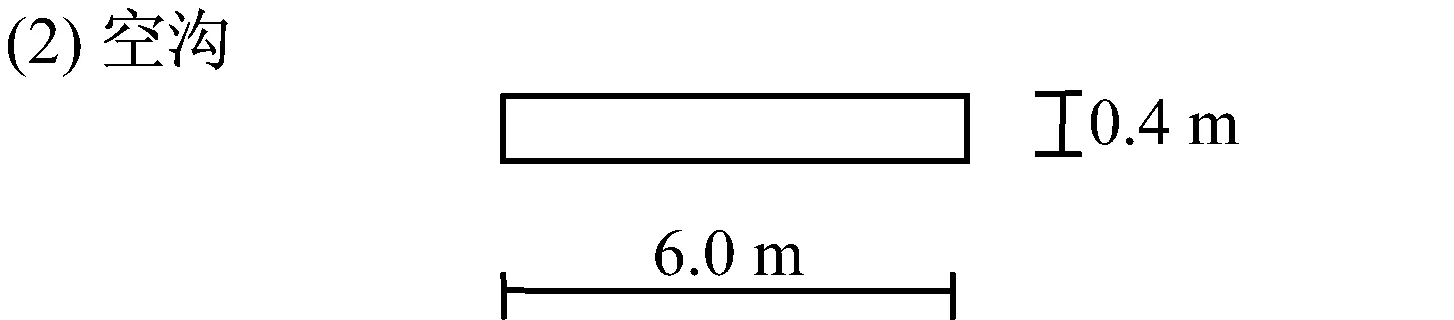
图4 单排柱腔屏障和空沟示意图Fig.4 A row of cylindrical cavities and an open trench

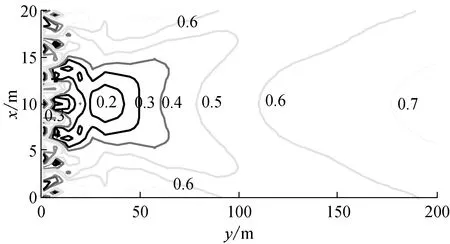
图5 单排柱腔屏障后的|uy/u0|等值线Fig.5 Contours of |uy/u0| behind a row of cylindrical cavities

比较图5和3(d)可以发现，8根半径为1.0 m的柱腔列构成的非连续屏障(屏障的整体宽度为23.0 m)对P波的隔离效果与长度为6.0 m、宽度为0.4 m的空沟基本相当，在y≤100 m区域的隔振效果均超过50%，屏障后近处的隔振效果均好于远处，上述现象可从弹性波的传播机理上可以进行如下解释，单排柱腔列的隔振效果主要取决于弹性波在柱腔之间空隙的透射，而空沟的隔振效果主要取决于弹性波在空沟两端的绕射，尽管空沟(连续屏障)的长度低于单排柱腔列的整体长度，但不产生透射，能更有效地截断弹性波的传播途径，因此空沟比单排柱腔列更有利于隔振。

4 结 论

运用复变函数的保角映射方法和波场势函数展开法，建立了有限长度的空沟对P波和SV波隔离问题的理论解，并给出了空沟对P波隔离的数值解答，通过对比分析得到以下主要结论：

(1) 随着空沟长度的增加，有效隔振效果明显提高，区域明显增大，对于宽度为0.4 m、长度为6.0 m的空沟，其对P波的隔离效果比较理想，屏障后y≤50 m区域的隔振效果超过70%；

(2) 由于空沟(连续屏障)不产生透射，在空沟长度远低于单排柱腔列(非连续屏障)整体长度的情况下，空沟对P波的隔振效果与单排柱腔列相当，因此，在场地和施工条件都允许的前提下，宜优先采用空沟进行隔振。

[1] 凌育洪, 吴景壮, 马宏伟.地铁引起的振动对框架结构的影响及隔振研究-以某教学楼为例[J].振动与冲击, 2015, 34(4): 184-189.

LING Yuhong, WU Jingzhuang, MA Hongwei.Effects of subway vibration on a frame structure and its vibration isolation[J].Journal of Vibration and Shock, 2015, 34(4): 184-189.

[2] WOODS R D.Screening of surface waves in soils[J].Journal of Soil Mechanics and Foundation Engineering.ASCE, 1968, 94 (4): 951-979.

[3] RICHART F E, WOODS R D.Vibration of soils and foundations[M].New Jersey: Prentice-Hall, INC, Englewood Cliffs, 1987: 130-142.

[4] ERKAN Ç, SEYHAN F, GÜNAY B, et al.Field experiments on wave propagation and vibration isolation by using wave barriers[J].Soil Dynamics and Earthquake Engineering, 2009, 29(5): 824-833.

[5] 徐平, 张天航, 石明生, 等.空沟对冲击荷载隔离的现场试验与数值模拟[J].岩土力学, 2014, 35(增刊1): 341-346.

XU Ping, ZHANG Tianhang, SHI Mingsheng, et al.In-situ test and numerical simulation of isolation of impact loads by open trenches[J].Rock and Soil Mechanics, 2014, 35(Sup1): 341-346.

[6] ULGEN D, TOYGAR O.Screening effectiveness of open and in-filled wave barriers: A full-scale experimental study[J].Construction and Building Materials, 2015, 86(5): 12-20.

[7] ADAM M, ESTORFF O.Reduction of train-induced building vibrations by using open and filled trenches[J].Computer Structure, 2005, 83: 1-24.

[8] 淳庆, 潘建吾.减振沟在强夯施工时的减振效果研究[J].振动与冲击, 2010, 29(6): 115-120.

CHUN Qing, PAN Jianwu.Vibration-isolating effect of vibration-isolating slot in the process of dynamic compaction construction[J].Journal of Vibration and Shock, 2010, 29(6): 115-120.

[9] 王晓, 严中保, 杜涵文.上海自由电子激光工程隔振沟减振数值分析[J].振动与冲击, 2012, 31(15): 190-194.

WANG Xiao, YAN Zhongbao, DU Hanwen.Numerical analysis of vibration-attenuation effect of trenches in the engineering project of Shanghai free electron laser[J].Journal of Vibration and Shock, 2012, 31(15): 190-194.

[10] 赵凯, 刘长武, 张国良.用弹性力学的复变函数法求解矩形硐室周边应力[J].采矿与安全工程学报, 2007, 24(3): 361-365.

ZHAO Kai, LIU Changwu, ZHANG Guoliang.Solution for perimeter stresses of rocks around a rectangular chamber using the complex function of elastic mechanics[J].Journal o f Mining & Safety Engineering, 2007, 24(3): 361-365.

[11] 徐平.多排桩非连续屏障对平面弹性波的隔离[J].岩石力学与工程学报, 2012, 31(增刊1): 3159-3166.

XU Ping.Isolation of Plane elastic waves by discontinuous barriers composed of several rows of piles[J].Chinese Journal of Rock Mechanics and Engineering, 2012, 31(Sup1): 3159-3166.

[12] LIU D K, GAI B Z, TAO G Y.Applications of the method of complex function to dynamic stress concentration[J].Wave Motion, 1982(4): 293-304.

[13] 徐平.多排柱腔列对平面P波和SH波的隔离[J].工程力学, 2011, 28(5): 78-83.

XU Ping.Isolations of plane P and SH waves by barriers composed of several rows of cylindrical cavities[J].Engineering Mechanics, 2011, 28(5): 78-83.

Theoretical analysis for isolation effect of an open trench on plane longitudinal waves

XU Ping

(School of Water and Environment, Zhengzhou University, Zhengzhou 450001, China)

An open trench with finite length was transformed to a unit circle with the conformal mapping method of complex functions, the boundaries of the trench were considered as free, theoretical solutions to isolation problems of longitudinal waves (P waves) and shear waves (SV waves) with an open trench were obtained based the wave function expansion method.The normalized displacement amplitudes were introduced, they were the ratios of displacement amplitudes of soil behind a barrier caused by both incident P or SV waves and scattering P and SV waves to those only by incident P or SV waves.Only incident P waves were taken as examples, and 4 trenches with a width of 0.4 m and lengths of 3.0 m, 4.0 m, 5.0 m and 6.0 m were analyzed.The results showed that the isolation effect and effective isolation zones increase obviously when the trench length increases from 3.0 m to 6.0 m, and the isolation effect exceeds 70% behind the trench when its length is 6.0 m, it reaches the in-situ test results of an open trench to isolate the impact loads.Finally, the isolation effect of an open trench and that of a discontinuous barrier composed of a row of cylindrical cavities were compared, and the results showed that because wave diffracting and trasmitting occur in a row of cylindrical cavities while only wave diffracting occurs in a trench, so the isolation effect of a trench with length of 6.0 m is equivalent to that of a row of 8 cylindrical cavities with a radius of 1.0 m, and so an open trench is the first and the best choice for the vibration isolation under the permission of field and operation conditions.

open trench; plane longitudinal waves; isolation effect; conformal mapping method; vibration isolation design

国家自然科学基金(51475164)；河南省高校科技创新人才支持计划(14HASTIT050)

2015-09-07 修改稿收到日期：2015-11-07

向玲 女，博士,教授，1971年生

TU435

A

10.13465/j.cnki.jvs.2017.05.011