一种用于海外项目投资优化组合的混合优化方法

华蓓，陈亚强，穆龙新，常毓文，翟光华

（中国石油勘探开发研究院，北京 100083）

一种用于海外项目投资优化组合的混合优化方法

华蓓，陈亚强，穆龙新，常毓文，翟光华

（中国石油勘探开发研究院，北京 100083）

在海外复杂合同模式及经营环境多变的情况下，针对如何实现产量、投资、效益、风险等多个目标优化配置的目标，文中确定了海外项目多目标投资组合优化的基本思路，表征了海外不同合同模式涉及的复杂商业规则和约束条件，建立了考虑时间维度及风险因子的多目标优化数学模型。通过将不同的优化算法进行结合，提出了一种求解多目标优化模型的混合优化方法。该方法先通过排队过滤生成满足目标和约束条件的投资组合解；然后以该解的特征参数作为约束条件进行线性优化，求出投资组合局部最优解；最后以该最优解作为初始投资组合通过遗传算法求解得到一系列投资组合可行解。利用该方法对海外重点地区项目开展了多目标投资组合优化，提出了不同情景下的优化方案和经营策略。

多目标；投资组合；优化模型；混合优化

0 引言

多目标优化是规划计划及投资组合优化中的关键问题之一［1］。海外业务的规模在日益扩大，但各项目存在的投资风险以及带来的收益存在很大差异。在目前低油价形势下，海外业务面临着如何科学地进行投资组合优化，合理地制定规划计划，从而解决将有限的资金投向哪些项目的优化决策问题。

国内油气项目规划和优化主要采用5年产量构成及自上而下的规划方法进行［2-4］，一些学者已经建立了一系列产量构成优化模型及多目标产量分配模型，主要围绕产量构成及各油区配产进行优化［5-6］。海外项目合同模式复杂多样，投资环境风险大，规划面临的突发事件多，产量构成变化快，国内的传统规划优化方法不适用于海外项目的规划和优化。本文以N个开发项目为研究范围，针对如何实现产量、投资、效益、风险等多个目标的优化配置，形成了海外项目非线性多目标投资组合优化方法。

1 海外项目多目标投资组合优化流程

一个完整的投资组合优化过程包括6个步骤：1）确认候选项目；2）定义项目商业规则和逻辑关系；3）设定多个约束条件及优化目标，建立优化模型；4）运用多种优化算法进行求解；5）对投资组合优化结果进行分析；6）根据期望选择最终投资组合。投资组合优化过程中涉及到建立优化数学模型、表征商业规则和约束条件、优化求解算法等理论和方法［7-9］。

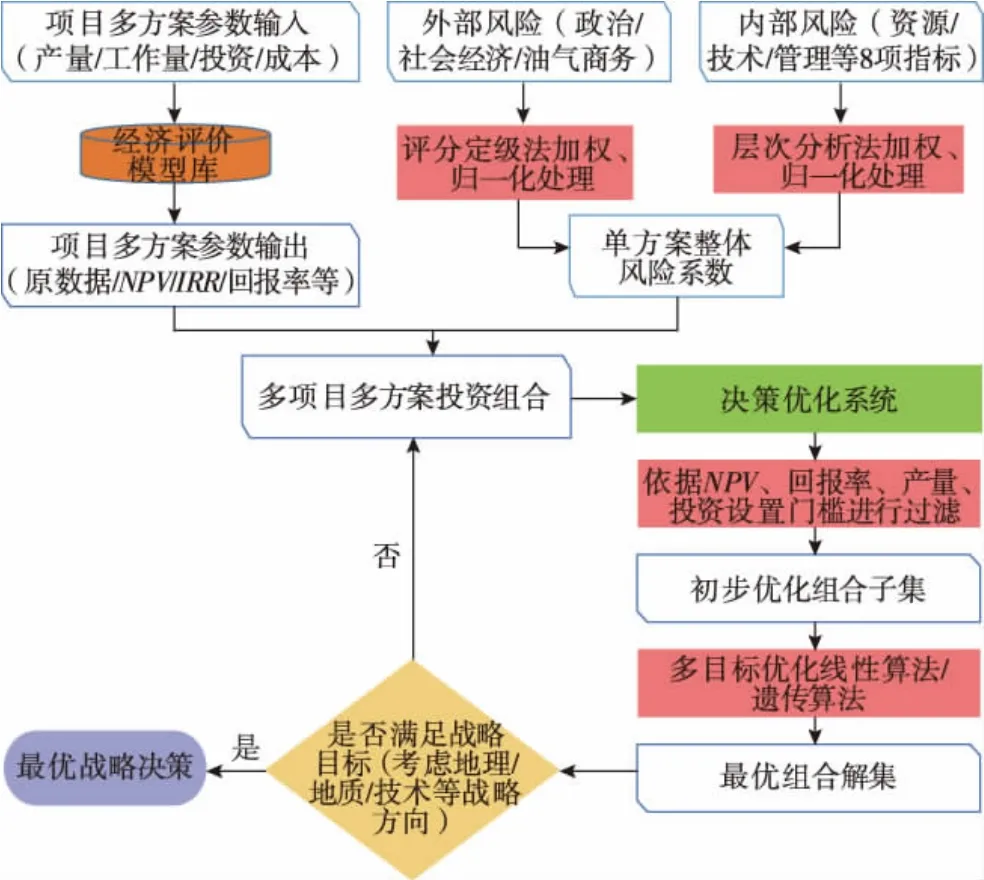
图1 海外项目投资组合优化流程

2 多目标优化数学模型

由于海外项目风险大，产量构成变化快，在建立多目标优化模型过程中，除考虑产量、投资、效益等指标外，还要考虑量化的风险因子，同时也需要对不同时间维度的约束条件进行表征。在此基础上，建立了考虑时间维度及风险因子的多目标优化数学模型。

该模型综合考虑净现值、产量和投资这3个目标。净现值和产量这2个目标与投资目标呈反向关系，为了追求净现值和产能的极大化，以及对应投资的极小化，采用相乘最大化的方法，建立优化模型。

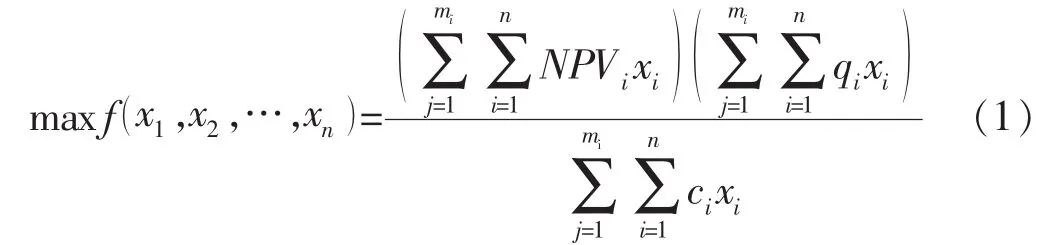
约束条件为

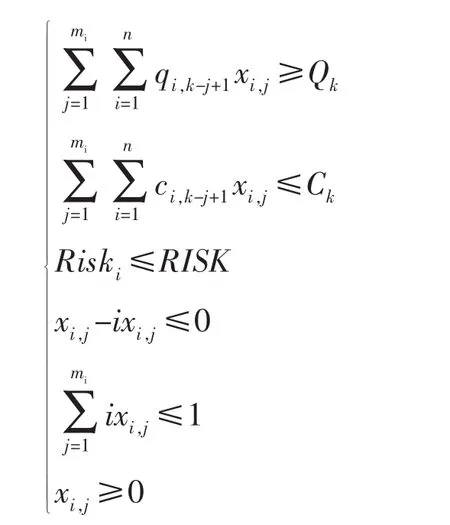
其中xi为0，1决策变量

式中：NPVi，j，qi，j，ci，j分别为项目i在j年的净现值、产量、投资；Riski为项目i的风险值，$；RISK为项目可接受的最大风险；Qk为第k年的总产量最低约束；Ck为第k年的总投资上限约束；n为待优选的项目总数；k表示不同的年份。

3 复杂商业规则和约束条件表征

海外项目合同模式主要有矿费税收制、产品分成制、服务合同制等3种类型，不同合同模式规定了投资者不同的权益和义务，包含多种复杂的商业条款及合同约定。尤其是对于某些一体化项目，各项目之间往往存在相互依赖关系或互斥关系，在项目的实施先后顺序上也相互制约、相互影响。因而在进行投资组合优化的过程中，需要对其中相关约束条件和商业规则进行表征。

投资组合优化过程中的商业规则和约束条件有着比较复杂的逻辑关系。主要包括：

1）设定项目（方案）之间的隶属关系和互斥关系。即对于多方案的项目，如果选择了其中高方案，则不能选择中、低方案；对于海外的一体化项目，如果选择了项目A，则必须也选择项目B（用If…then数学语句）。

2）设定至少（至多）选择的项目组个数。即在某个投资组合中最少或最多选择的项目个数，使用语句At most…of，At least…of，Exactly实现。例如：考虑到中东地区资源国政治经济风险较大，在投资组合中中东地区项目最多选择5个；考虑到中亚地区项目稳定并且收益较高，在投资组合中中亚地区项目最少选择7个。

3）设定项目实施时间排序。如果项目A在某年开始实施，则要求项目B必须在某年之前（或之后）开始实施。

4 基于不同算法的混合优化方法

目前，对于多目标优化模型的求解算法主要包括排队过滤法、线性优化法、遗传算法、蚁群算法等［10-13］。每种算法都有其优缺点和适用性［14-15］。根据目标函数和约束条件的线性与非线性，优化模型可分为线性模型和非线性模型。这2种模型有各自适用的优化算法，通过具体模型运行结果对比可得出不同种类的模型所适用的优化算法。

这里选取了2种具有代表性的模型：净现值（NPV）最大模型（见式（2）约束条件同式（1）），此为线性模型；内部收益率（IRR）最大模型（见式（3）约束条件约束条件同式（1）），此为非线性模型。在相同投资和产量约束条件下，选用不同的算法优化结果对比如下：

从表1看出：对于净现值最大模型，线性优化求得的净现值、产量、内部收益率等指标要明显好于遗传算法；对于内部收益率最大模型，线性优化求得的组合内部收益率要低于遗传算法优化结果。由于净现值最大模型为线性模型而内部收益率模型为非线性模型，因此，对于线性模型，用线性优化方法求解即可。而对于非线性模型，则须用遗传算法等搜索算法进行求解。

在投资组合优化中，排队过滤法、线性优化和遗传算法各有其优劣和适用性（见表2）。

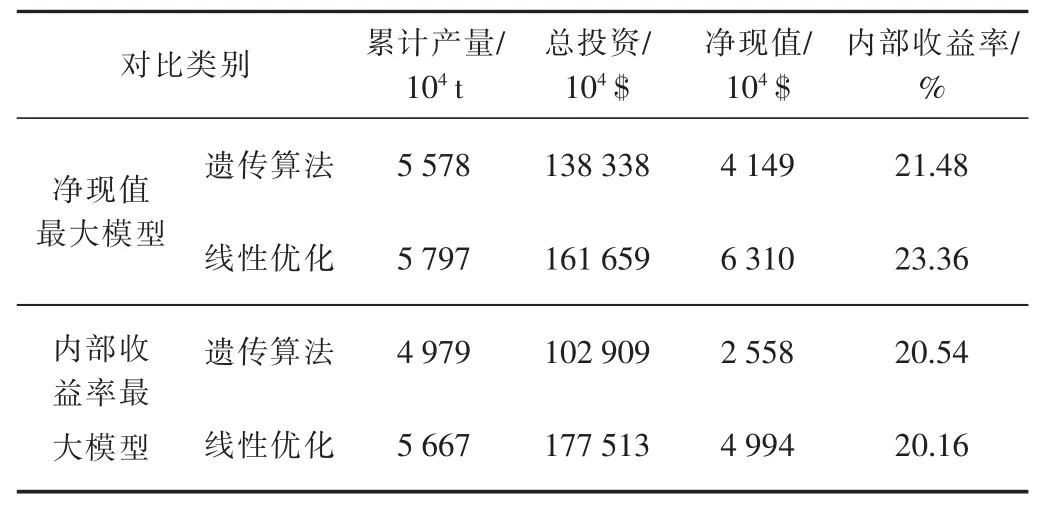
表1 不同优化模型运用不同的算法优化结果

表2 不同优化算法特点对比

鉴于以上3种优化方法各有优缺点，为了能对优化模型进行更好的求解，将这3种优化方法进行互相结合，形成了混合优化方法。如图2所示：该方法首先通过排队过滤法生成满足目标和约束条件的投资组合解；然后以该投资组合解的特征参数作为约束条件进行线性优化，求出局部最优解；最后把线性优化求得的局部最优解作为初始投资组合通过遗传算法求解得到一系列可行的投资组合。

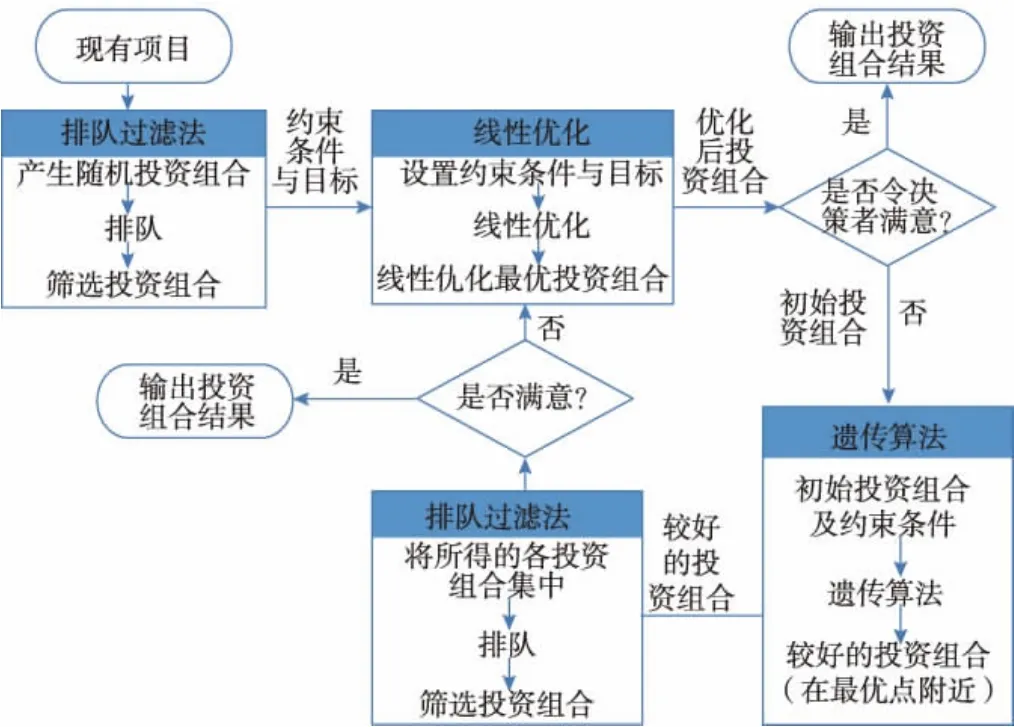
图2 混合优化方法示意

5 多目标优化实例

基于上述形成的多目标投资组合优化模型及方法，以N个开发项目作为研究范围。

5.1 优化方案1：限定N个开发项目均入选

优化目标和约束条件包括产量、投资、净现值、风险等。商业规则是：对每个候选项目进行多个方案互斥规则的设置，确保在优选的投资组合中每个项目只有其中之一方案被选中。由于模型为非线性模型，用遗传算法求解。表3，4为本次执行遗传算法的约束条件及相关参数设置情况。

表3 相乘最大化模型约束条件赋值

表5可看出，优化后的指标与优化前高方案相比，投资减少1.5%，净现值增加12%，内部收益率提高3.2%。可以看出，优化后的投资组合在满足历年产量目标和投资约束的情况下，同时实现了净现值最大化。

表4 遗传算法的参数设置情况

表5 方案1优化前后结果对比

5.2 优化方案2：不限定N个开发项目均入选

优化目标和约束条件与优化方案1相同，在商业规则的设置上，考虑可以出售较差项目资产，因此不限定N个开发项目均入选。

表6可看出，经过优化，最后选中了M个项目，有6个项目被优化掉。优化后的指标与优化前高方案对比显示，投资减少13.4%，净现值增加18.4%，内部收益率提高4.79%。总体来看，优化方案2的各经济指标好于优化方案1，可实现投资重点更加突出，布局更加均衡合理。

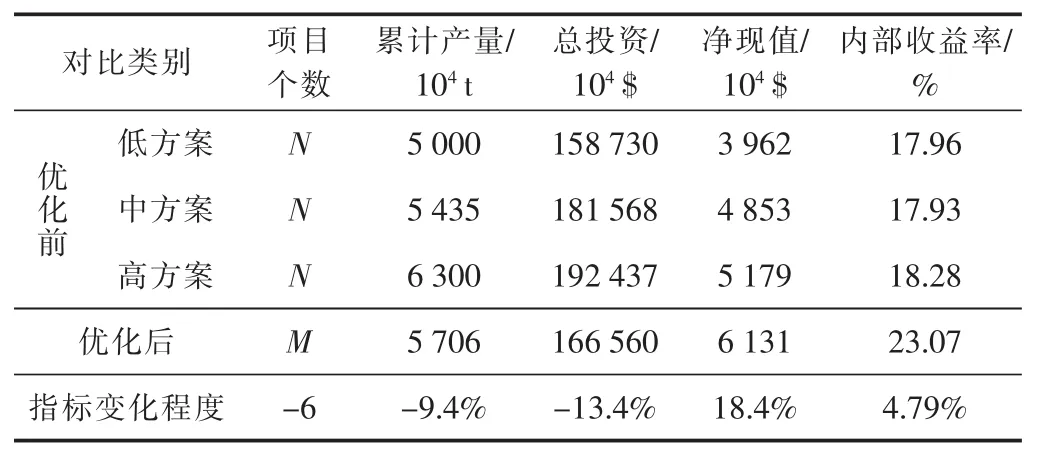
表6 方案2优化前后结果对比

5.3 混合优化方法实例

第1步，Merak软件的Capital Planning模块能够帮助生产满足约束条件的投资组合。本次利用该模块生成了100个有效的投资组合。将100个投资组合模型按照净现值大小进行过滤，优选出了其中的一个投资组合。所选投资组合的产量和净现值在所有投资组合选项中均排名第一（见表7）。

表7 过滤法选中的投资组合关键指标

第2步，在排队过滤的基础上进行线性优化。在给定最小总产量、最大总投资约束的情况下，追求净现值最大化。这里将排队过滤法发现的解特征值（见表6）作为线性优化执行过程的约束条件。求解得出一个线性优化最优解（见表8）。

线性优化求解得出的投资组合净现值为6 572× 104$，该值比利用排队过滤法得出的投资组合净现值高14%；线性优化求得的投资组合总产量为5 762×104t，比排队过滤法得出的投资组合总产量高12.7%。同时，对于线性优化求得的投资组合而言，总投资减少了279×104$，内部收益率提高到23%。

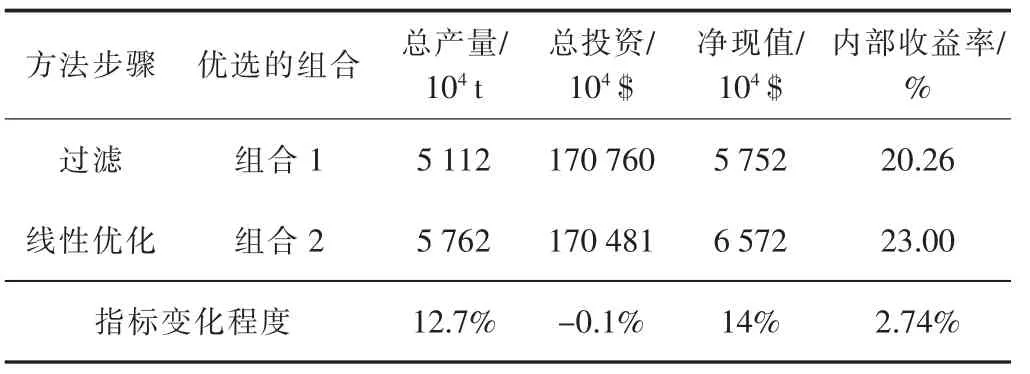
表8 过滤法和线性优化得出的投资组合关键指标对比

第3步，在过滤法和线性优化得到2个投资组合解的基础上，将过滤所得的投资组合解特征值作为约束条件，将线性优化获得的投资组合解作为初始投资组合，利用遗传算法进一步寻找期望的投资组合。遗传算法使用的目标函数和约束条件与线性优化中使用的目标函数和约束条件一致。对遗传算法所得的投资组合进一步优选，优化结果见表9。

表9 利用不同算法得出的投资组合关键参数对比

通过上述3步，最终得出了一个期望的投资组合3。通过不同步骤优选出的投资组合，对比可以看出，组合3的总投资最小，总产量和内部收益率介于组合1和组合2之间。组合3用较少的投资实现了产量、投资、效益之间的平衡，因此可定为期望的投资组合。

上述混合优化方法的优化过程从排队过滤法开始，将排队过滤法求解得出的首选投资组合特征值作为线性优化的约束条件，通过线性优化针对设定的约束条件和目标识别局部最优解，最后以该解作为初始投资组合，利用遗传算法得出最优解附近的一系列可行投资组合并确定期望的投资组合。

6 结论

1）建立了一套考虑时间维度及产量、投资、效益、风险等多个指标的非线性多目标投资组合优化模型。在模型中纳入了量化的风险因子，并对海外复杂合同模式下各投资单元之间的逻辑关系和商业规则等约束条件用数学语句进行了表征。

2）提出了一种求解该类非线性模型的混合优化方法，该方法先用过滤法生成初始投资组合解，然后此投资组合的特征参数作为约束条件进行线性优化，求出局部最优解，最后以该解作为新的起点用遗传算法求解得到一系列有效的投资组合。

3）利用本文所建立的模型及方法对海外项目、重点地区开展了多目标优化实践。根据不同的目标和期望提出了相应的优化策略。该方法为构建海外战略规划决策支持系统奠定了理论基础，已经在海外 “十三五”规划及海外项目经营策略优化中得到应用。

［1］ 常毓文，潘志坚，于立君，等.油气开发战略规划理论与实践［M］.北京：石油工业出版社，2010：15-28.

［2］ 曲德斌，李丰.油气开发规划优化方法及应用［M］.北京：石油工业出版社，2013：18-24.

［3］ 刘志斌，丁辉.油田开发规划产量构成优化模型及其应用［J］.石油学报，2004，25（1）：62-65.

［4］ SHOLARIN E A.Applying integrated projectmanagement methodology to hydrocarbon portfolio analysis and optimization［R］. SPE 100967，2006.

［5］ PRAKASH D.Decision making in upstream oil and gas industry-an integrated approach［R］.SPE 154999，2012.

［6］ 程伟，张广杰，董伟宏，等.油气田开发规划模型的建立及求解［J］.大庆石油学院学报，2006，30（2）：112-115

［7］ RODNEY W L.Portfolio optimization techniques for the energy industry［R］.SPE 82012，2003.

［8］ WILLIGERS BjA，WEIS F.Creating portfolio insight by a pratical multi-method optimisation approach［R］.SPE 146583，2011.

［9］ WILLIGERS BjA，MAJOU F.Creating efficient portfolios that match competing corporate strategies［R］.SPE 129259，2010.

［10］张在旭.油田开发系统规划的策略［J］.石油大学学报（自然科版），1998，22（2）：75-78.

［11］范玉妹.数学规划及其应用［M］.北京：冶金工业出版社，2009：68.

［12］MICHAEL J，BACK C G.Portfolio management for strategic planning and operational optimization［R］.SPE 134339，2010.

［13］LUIS R，BRIAN M.Portfolio optimization in high and low risk environments［R］.SPE 159603，2012.

［14］MICHAEL B，GRAHAM K.An integrated portfolio management approach for more effective business planning［R］.SPE 162748，2012.

［15］APRIL J，GLOVER F.Advanced optimization methodology in the oil and gas industry：the theory of scatter search techniques with simple examples［R］.SPE 82009，2003.

（编辑 赵旭亚）

Multi-objective portfolio optimization method for overseas oil&gas projects

HUA Bei,CHEN Yaqiang,MU Longxin,CHANG Yuwen,ZHAI Guanghua
(Research Institute of Petroleum Exploration＆Development,PetroChina,Beijing 100083,China)

Portfolio optimization is a multi-objective one which means we need to consider several factors such as production, investment,revenue and risk of overseas projects at the same time in the circumstances of complicated contract models and fickle business environments.Thus,a multi-objective optimization model has been developed for overseas projects.In this model,the intricate business rules,corporate strategies and constraints in the overseas contract models are mathematically characterized.And both the time dimension and the risk factor have been taken into account.Based on the analysis of different optimization methods,a hybrid optimization method was developed and put forward for this multi-objective model.The hybrid method starts with the"rank& cut"method and the best portfolio generated by it is regarded as the constraints for the linear planning.And the genetic algorithm is used to seek the alternative portfolios near the local optimum solution generated by linear planning.This method was well applied in the optimization and planning process of overseas projects and some optimization operation strategies were raised and suggested according to different scenarios.

multi-objective;portfolio;optimization model;hybrid optimization

中国石油天然气股份有限公司重大科技专项课题“海外油气田开发潜力评价及开发策略和决策支持系统研究”（2011E-2510）

TE32+2

A

10.6056/dkyqt201702022

2016-10-01；改回日期：2017-01-10。

华蓓，女，1991年生，在读硕士研究生，研究方向为海外油气田开发及规划方面的研究。E-mail：bhyn3@petrochina.com. cn。

华蓓，陈亚强，穆龙新，等.一种用于海外项目投资优化组合的混合优化方法［J］.断块油气田，2017，24（2）：238-242.

HUA Bei，CHEN Yaqiang，MU Longxin，et al.Multi-objective portfolio optimization method for overseas oil&gas projects［J］.Fault-Block Oil& Gas Field，2017，24（2）：238-242.