单箱多室斜交箱梁受力性能分析
2017-04-07肖运栋
肖 运 栋
(深圳市华方工程设计顾问有限公司,广东 深圳 518001)
单箱多室斜交箱梁受力性能分析
肖 运 栋
(深圳市华方工程设计顾问有限公司,广东 深圳 518001)
介绍了斜交箱梁的特点,通过建立某工程的ANSYS模型,考察箱梁在自重及预应力作用下,不同斜交角对箱梁支反力、剪力滞效应的影响,并总结了斜交箱梁桥的支反力变化,得出不同斜交角、跨中横隔板对斜交箱梁桥不利截面的剪力滞效应分布规律,提出了该种桥型的设计建议。
斜交箱梁,斜交角,剪力滞,支反力,横隔板
在城市的快速发展中,一些现有道路越来越不能满足日益增长的交通需求。为解决人民群众的出行需要,需要在现有道路节点上新建立交以疏解交通。面对现有道路节点的制约,经常性的出现桥梁以斜交方式跨越现有道路。
由于斜交角的存在,造成各腹板受力不一致,会引起支反力的变化,这对支座的选取及下部结构的设计有着非常大的影响。
根据梁弯曲初等理论的平截面假定,不考虑剪切变形对位移的影响,弯曲正应力沿梁宽度方向是均匀分布的,但是在箱型梁中,由于翼板剪切变形的不均匀性,弯曲应力沿梁宽度方向也是不均匀分布的,这种现象称之为“剪力滞”现象[1]。在以前的工程设计中,剪力滞效应如果考虑不周,将会导致箱梁的应力集中,可能继续恶化为桥梁损毁,如澳洲、欧洲等国发生的重大钢箱梁事故,国内佛陈大桥、顺德立交等桥梁的翼缘板横向裂缝问题等。目前,国内外对箱梁的剪力滞效应多集中在正交桥梁上,对斜交桥梁的研究资料偏少。鉴于单箱多室斜交箱梁的受力性能、传力路径等方面都与正交箱梁有所区别,其空间效应随着桥梁宽度的增大也有较大变化,因此有必要对单箱多室斜交箱梁进行研究。
在斜交箱梁的设计中,设计人员通常将斜交箱梁简化为单根杆系梁,只在支座约束上反映斜交,亦或采用剪力柔性梁格法[2]。前者无法反映斜交角对箱梁空间受力的影响,特别对于斜交角度比较大的情况;后者对于一般箱梁来讲,计算前对箱梁的梁格特性处理较为繁琐,容易造成人为偏差[3]。本文利用ANSYS有限元软件对不同斜交角的箱梁进行三维实体建模,分析斜交角对箱梁受力性能的影响。
1 工程背景
本次研究对象为一跨线立交桥,桥跨布置为(30+36+30)m现浇预应力混凝土连续箱梁桥,桥面宽度为16.0 m。端横梁与道路中心线正交;中横梁与道路中心线斜交,斜交角为30°。桥梁采用等高单箱四室布置,梁高为1.9 m,端横梁宽1.6 m,中横梁宽2.2 m,中跨跨中设置40 cm厚的横隔板一道(见图1,图2)。
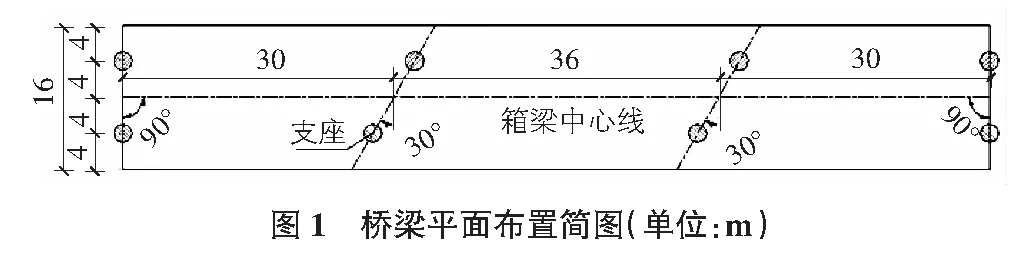
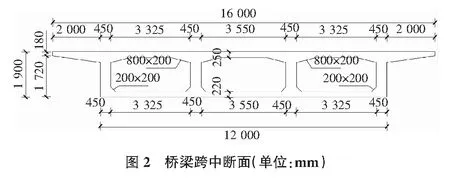
2 有限元模型的建立
箱梁采用Solid65单元,预应力钢束采用Link8单元。本文拟根据不同的斜交角(0°,15°,30°,45°)分析斜交箱梁在支座反力上的差异,考虑在箱梁自重及预应力下的剪力滞效应。
考虑到不同的斜交角度,本文采用ANSYS参数化语言(APDL)进行建模,预应力钢束与周围混凝土采用耦合约束,预应力的施加采用等效降温法,即预应力的降温值为:
(1)
其中,ΔT为预应力的降温值;α为预应力的线膨胀系数;σ为预应力的应力。
图3为ANSYS的斜交箱梁断面网格划分图(斜交角30°)。
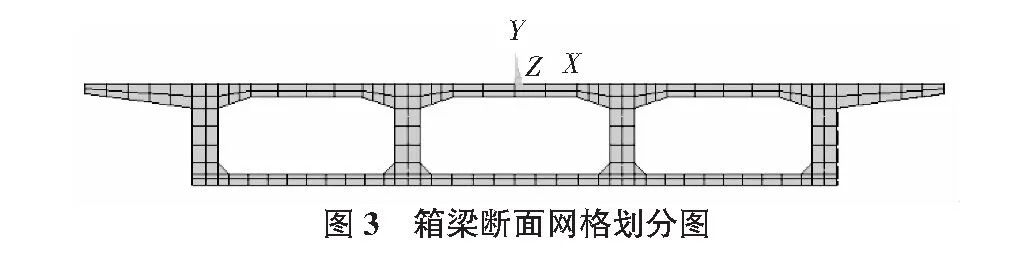
3 斜交箱梁支反力分析
本次分析只考虑箱梁自重与预应力的作用,图4,图5为不同斜交角(0°,15°,30°,45°)下箱梁的支反力分布情况,其中“杆系”为将斜交箱梁简化为单根杆系梁,只在支座约束上反映斜交的方法,计算软件采用MIDAS Civil。
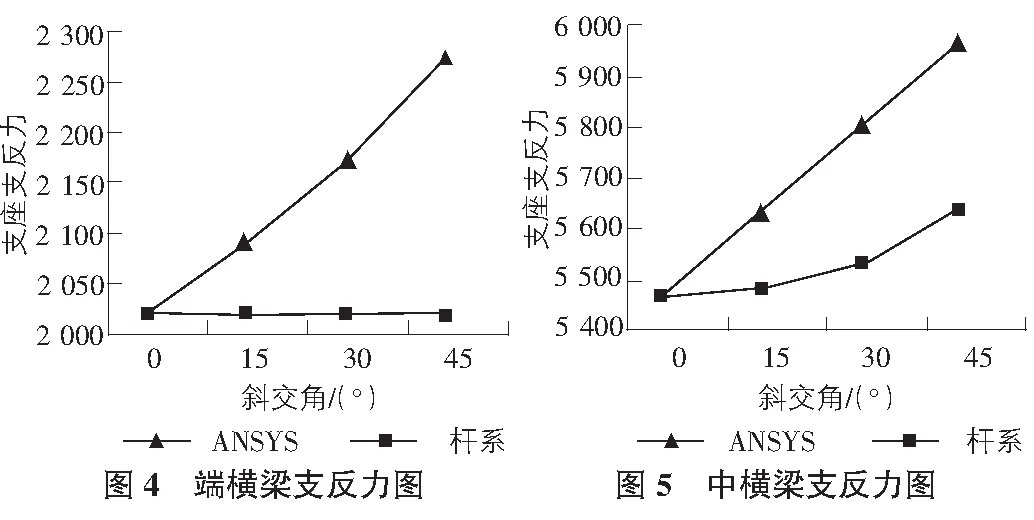
从图4,图5中可以看出:
1)“杆系”方法未能反映斜交角对支反力的影响,特别是端横梁。随着斜交角的增大,两者差值逐渐增大,在斜交角为45°时,端横梁支反力两者差值为13%,中横梁支反力两者差值为6%。由此可见,“杆系”方法未能准确体现各腹板的受力,设计时应予以注意。
2)通过ANSYS数据可知,支反力随着斜交角近似线性变化,本例端横梁为5倍斜交角差值变化,中横梁为11倍斜交角差值变化。
4 斜交箱梁剪力滞分析
在工程上一般用剪力滞系数λ来描述箱梁剪力滞效应[4]:
(2)
本次分析只考虑箱梁自重与预应力的作用,图6~图9为不同斜交角(0°,15°,30°,45°)下箱梁中横梁附近断面(横梁受支座影响,无法体现各腹板的剪力滞效应)、跨中位置的顶底缘剪力滞情况,其中箱梁横断面各点位置为0处代表箱梁横向的中心处。
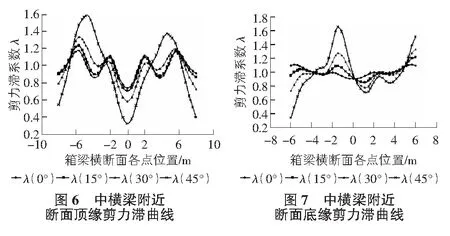
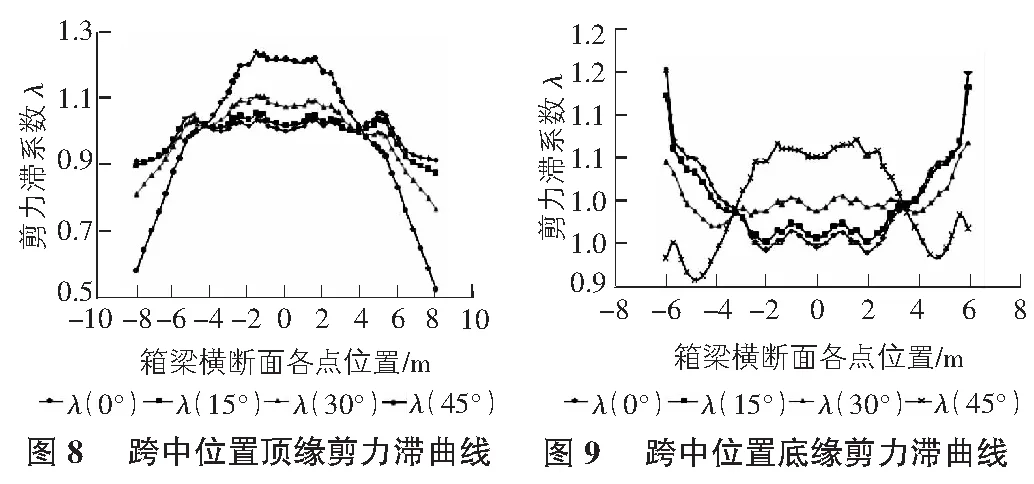
从图6~图9中可以看出:
1)从总体上看,单箱多室斜交箱梁的剪力滞系数与正交箱梁相比,无论在变化幅度还是变化趋势上,都有区别。斜交角度的增大,会加剧剪力滞效应的变化。
2)在中横梁附近截面顶缘,由于斜交角的存在,两外腹板的顶缘剪力滞效应变化明显,应力随斜交角的增大向两外腹板集中,其中在斜交角45°时,剪力滞最大为1.6,而正交桥仅为1.18。而翼缘板及箱梁截面中心出现负剪力滞效应,应力随斜交角的增大有逐渐减小的趋势,斜交角越大,减小越大。
3)中横梁附近截面底缘,四道腹板的剪力滞效应变化显著,呈现近似反对称变化的形式,两外腹板、中腹板的剪力滞变化方向相反。正应力逐渐向斜交角倾斜方向靠里腹板积聚,其中在斜交角45°时,剪力滞最大为1.65,而正交桥仅为0.97。在计算时,还应充分考虑外腹板的负剪力滞效应。
4)对于跨中截面,其剪力滞效应随斜交角的变化不如中横梁附近截面变化的剧烈,斜交情况下跨中截面的最大剪力滞系数比正交情况稍大,顶板最大剪力滞系数为1.24,底板最大剪力滞系数为1.15。由于斜交角的增大,跨中底板底缘在箱梁截面中心的剪力滞效应由负变正,外侧腹板剪力滞效应由正变负,说明应力逐渐向箱梁中心集中。设计时应注意这种变化。
针对跨中剪力滞的分布情况,本文选取斜交角为30°时,跨中是否有横隔板情况下进行剪力滞分析,其中箱梁横断面各点位置为0处代表箱梁横向的中心处。

从图10,图11中可以看出:
跨中横隔板剪力滞影响不大,无跨中横隔板顶缘的最大剪力滞系数为1.12,有跨中横隔板顶缘的最大剪力滞系数为1.07,相差仅4.1%;无跨中横隔板底缘的最大剪力滞系数为1.07,有跨中横隔板底缘的最大剪力滞系数为1.04,相差仅2.8%。由此得出横隔板对剪力滞系数并无太大影响。
5 结论和建议
1)单箱多室斜交箱梁斜交角的变化对支座支反力有影响,支反力变化与斜交角呈线性关系;“杆系”方法未能反映斜交角对支反力的影响,与实际结果有差异。计算时,应充分考虑斜交角的影响,采用更合适的方法进行复核。
2)单箱多室斜交箱梁的剪力滞效应与正交桥相比变化很大,随着斜交角的增加,剪力滞变化越剧烈。在中横梁附近位置,顶缘剪力滞系数关于箱梁中心近似对称变化,应力随斜交角的增大向两外腹板集中;底缘出现剪力滞系数反对称,特别是外腹板变化尤大。由于存在斜交角的影响,故在针对单箱多室斜交箱梁的计算中,应采用更为精确的计算方法,模拟各道腹板的受力。
3)本文通过对30°斜交角箱梁的分析,表明跨中横隔板对跨中剪力滞效应并无太大影响。
[1] 郭金琼,房贞政,郑 振.箱型梁设计理论[M].北京:人民交通出版社,2008.
[2] E.C.汉勃利.桥梁上部构造性能[M].北京:人民交通出版社,1982.
[3] 杨志华.梁格法在混凝土连续箱梁桥计算中的应用[J].中国水运(理论版),2006,4(5):69-70.
[4] 范立础.桥梁工程(上册)[M].北京:人民交通出版社,2008.
Analysis on stress performance of skew box girder with single box and multi-chamber
Xiao Yundong
(ShenzhenHuafangEngineeringDesignConsultingCo.,Ltd,Shenzhen518001,China)
The thesis introduces features of skew box girder. Through establishing the engineering ANSYS model, it monitors the impact of different skew angles upon box girder bearing reaction force and shear-lag effect under self-weight and prestress of the box girder, summarizes bearing reaction force alteration of the skew box girder bridge, obtains negative section shear-lag effect distribution law of different skew angle and middle-span diaphragm board, and finally puts forward the bridge design suggestions.
skew box girder, skew angle, shear-lag, bearing reaction force, diaphragm board
1009-6825(2017)06-0205-02
2016-12-11
肖运栋(1985- ),男,工程师
U441
A
