气液两相流摆动特性实验的数值模拟

马 霞，李国栋，范翠香，高 扬

西安理工大学，陕西 西安 710048

气液两相流摆动特性实验的数值模拟

马 霞，李国栋，范翠香，高 扬

西安理工大学，陕西 西安 710048

为了给鼓泡塔反应器设计提供依据，运用计算流体力学（CFD）软件模拟了鼓泡塔气液两相流动态行为。采用双欧拉法对鼓泡塔矩形反应器内不同曝气量下气液两相流的摆动特性进行了模拟考察，液相采用标准κ-ε紊流模型，气相采用分散相零方程模型，分析了网格尺寸、时间步长以及相间作用力对模拟结果的影响，模拟的曝气量为42.5～237 mL/s。结果表明，当相间作用力仅考虑阻力时，气液两相流呈现周期性摆动规律；随着气流量的增加，气泡羽流的摆动幅度和频率增大，同时液体的气含率也在增加；模拟的气液两相流摆动频率数据与实验值吻合较好，两者的相对误差为7.2%～12.9%。

鼓泡塔 气液两相流 摆动特性 双欧拉κ-ε模型

鼓泡塔是一种气液两相流反应器，气体从塔底部喷入，形成分散的气泡群，气泡群在液体中上升，同时带动液体向上运动，气泡羽流两侧会产生向下的液体流动，流动现象复杂多变，已有大量关于此类流动问题的文献发表[1-5]，其中矩形反应器内气泡群流动一直是实验和数值模拟研究的热点，但是由于流动特性与反应器结构及操作方式有很大的关系，此类反应器的设计和放大仍然是一个问题。

与传统的实验方法相比，数值模拟具有耗费小、可重复等优点，能够预测实验难以测量的局部流场细节。目前气液两相流模拟主要有欧拉-拉格朗日法[6-8]和欧拉-欧拉法[9-14]（双欧拉法）两种方法，欧拉-欧拉法的计算不受气含率的限制，计算资源相对低[14]。利用双欧拉κ-ε模型进行三维模拟可以复现气泡羽流的周期性运动特性[1,11-17]，但对于相间作用力仍存在争议，Sokolichin等[11,12,15]认为，阻力对气液两相流的摆动特性影响较大，虚拟质量力对模拟结果的影响不明显；Mudde等[14]报道，为了准确模拟气泡羽流的振荡周期和速度场，还应考虑虚拟质量力与阻力；并且，不同的学者采用了不同的阻力模型。本研究采用计算流体力学（ANSYS14.0中CFX5）软件，采用欧拉-欧拉法结合标准κ-ε紊流模型，基于Enrique Juliá等[18]的实验结果，对鼓泡塔内气液两相流的摆动特性进行三维数值模拟，考察不同的网格尺寸、时间步长、相间作用力（阻力、升力和虚拟质量力）的影响，选择出适宜的参数和模型以能够较为准确地模拟鼓泡塔内气液两相流的摆动特性，以期为提高鼓泡塔反应器混合效率提供依据。

1 反应器结构及模型

基于Enrique Juliá的实验结果[18]，建立图1所示反应器计算模型，其中鼓泡塔宽度W（沿X方向）为264 mm、厚度B（沿Z方向）为31 mm、高度H（沿Y方向）为792 mm，坐标原点位于模型底部

式中，σ为湍流Prandtl数。

(4) 相间动量传递模型：

两相之间的作用力可以表示为：

式中，CD为阻力系数，阻力系数分别采用CD为0.66[12]和Grace阻力模型：

式中，Vb为气泡的最终速度，db为气泡直径，M为莫顿数，E0为奥托斯数。μref为0.000 9 kg/(m·s)。

式中，CL为升力系数；CV为虚拟质量力系数。

(5) 初始条件和边界条件

本研究采用计算流体力学（ANSYS14.0中CFX5）软件模拟求解。

边界条件设置：液相（水）的进口速度为0 m/s，空气的进口速度是气体流量的函数；出口边界为自由液面边界条件，气相：允许逸出，液相：认为是自由滑移的壁面，不允许流出；壁面：液相采用无滑移边界条件，气相采用自由滑移边界条件。

初始计算条件：t为0 s时刻计算区域内充满水，即设水的体积分数为1，空气的体积分数为0；初场内水静止不动，速度为0 m/s。

进口气流量Q0为42.5，82.5，125，237 mL/s，根据文献[18]，对应的当量气泡直径分别为3.8，4.3，5，6.1 mm。水动力方程组采用有限体积法进行求解。离散格式采用混合格式。

3 结果与讨论

3.1 网格尺寸与时间步长的选择

随着网格尺寸变小，轴向速度的时均模拟值和实验数据出现了较大离散[1,3,12]。为了研究网格尺寸对求解结果的影响，在如下计算工况计算了网格的影响（见表1）：时间步长t为0.025 s，进口气流量Q0为237 mL/s（相应地气体表观速度为2.9 cm/s），计算当量气泡直径D为6.1 mm。从表1可以看出，粗、中、细三种网格下气泡羽流摆动频率f的模拟结果与实验结果的相对误差分别为7.2%、8.8%、12.8%，在点A1（0, 0.2ymax, 0）位置处液相垂向速度的时均模拟值与实验值的相对误差分别为2.4%、15%、12.7%。与粗网格相比，中、细网格下气泡羽流的摆动频率、时间平均的液相轴向速度的模拟值表现出相对误差增加的趋势，但从总体上三者差异不大。考虑到粗网格下模拟结果与实验结果吻合得最好，除非特别指出，以下研究的网格均为粗网格。

表1 网格尺寸对计算气体气含率、摆动频率和液相垂向速度的影响Table 1 Effect of mesh size on the calculated plume gas hold-up, oscillating frequency and vertical liquid velocity

时间步长对模拟结果的影响见表2，时间步长为0.25，0.025，0.01 s。时间步长与CFL数（柯朗数）有关，即：其中v是气相垂向速度，Δy是单元尺寸；Δt是时间步长。考虑到单元尺寸为粗网格尺寸，且气泡最终的上升速度经验值为0.3 m/s，则依据CFL准则可得出：Δt≤0.036 s。因此，根据表2的计算结果，计算步长最终选为0.025 s，一方面Δt为0.025 s证明了CFL准则，另一方面，更小的时间步长对模拟结果的影响不明显。

表2 时间步长对计算气体气含率、摆动频率和液相垂向速度参数的影响Table 2 Effect of time-step on the calculated plume gas hold-up , oscillating frequency and vertical liquid velocity

3.2 阻力、虚拟力和升力的作用

为了研究相间作用的影响，模拟了不同作用力的影响。工况A仅考虑阻力的影响，阻力系数采用常阻力系数Cd为0.66和变阻力系数Grace模型，计算结果见表3。气泡尺寸分布的实验情况表明[18]，气泡尺寸均匀，且呈椭球状，尺寸范围较窄，大多数气泡直径为4.3～5.1 mm，气泡没有发生聚并和破碎。Grace阻力模型考虑到了气泡的变形，阻力系数随着气泡的形状而变化。考虑到实验中气泡直径范围窄且变形小，可近似认为椭球体，阻力系数按常值考虑更为合理，气泡羽流的摆动频率计算结果也证实了这一点。因此在以下研究中阻力系数按Cd为0.66计算。

表3 不同的阻力模型对计算气体空隙率和摆动频率参数的影响Table 3 Effect of different drag force model on the calculated gas hold-up and plume oscillating frequency parameters

工况B考虑阻力和虚拟质量力的影响，当虚拟质量力系数为0.5时，B工况下气泡羽流摆动频率的计算值为0.133 Hz。在本研究的进口气流量范围内，相间作用力仅考虑阻力项与考虑阻力和虚拟质量力相比，两者对气泡羽流摆动频率的影响差别很小，原因在于由虚拟质量力产生的流体加速运动是很小的，可忽略。

工况C考虑阻力和升力的影响，升力系数取为0.5，对于较高的进口气流量时，工况C会使气泡羽流摆动频率的模拟值（f=0.162 Hz）过高估计。事实上，在这种情况下，因为进口速度高，使得液相产生较高的剪切率，升力的作用尤其显得重要。数值模拟结果与实验结果不一致，主要是升力系数取值可能不合理，有关这方面的研究不充分导致。

基于以上分析，本文研究中相间作用力仅考虑阻力，不考虑升力、虚拟质量力的影响。

3.3 瞬态模拟结果

进口气流量Q0为237 mL/s时xy（z = 0 m）平面上气相体积分数与液相速度矢量分布瞬时图见图2。图2(a)～(d)显示了从90～97.3 s时气泡羽流摆动的一个周期，约7.3 s，呈现了低频振荡特性，这是由垂向流动的不稳定的旋涡结构诱发的。气泡群从底部曝气区释放出来，沿着区域中心线缓慢上升，周边的液体不断地被卷吸到羽流中，在卷吸作用下气泡向中心聚集，形成带有蘑菇云的气泡柱，在气泡柱两侧液体向下流动，形成左、右两旋涡环流，受气泡尺寸、气泡上升速度、周围壁面等影响，卷吸作用不对称，迫使羽流两侧压差不相等，使得羽流偏离原平衡位置，出现左右旋涡上下交错、垂向流动，旋涡结构不稳定，气泡柱呈蛇形摆动，从而使气泡羽流发生了低频振荡。

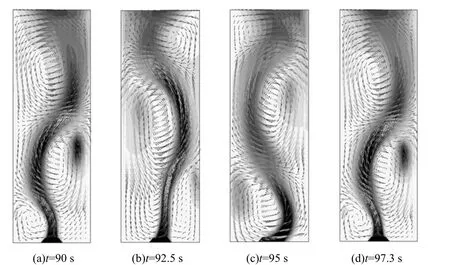
图2 气相体积分数云图与液相速度矢量分布Fig.2 Distribution of gas hold-up represented by contours and the vector distribution of vertical liquid velocity represented by arrows

3.4 摆动频率

图3给出了Q0为237 mL/s时液相垂向速度在位置点A（0.5xmax, 0.2ymax, 0）处随时间变化的模拟结果与实验结果曲线。当Q0为237 mL/s时，液相垂向速度的振幅模拟值在±0.6 m/s内，数值模拟结果与实验值基本一致。采用快速傅立叶变换对图3(a)中数据进行处理，相应的频谱特性曲线见图3(b)：对于模拟数据，在f为0.131 Hz处达到峰值，即该羽流的摆动频率为0.131 Hz，摆动周期为1/f为7.63 s；对于实验数据，在f为0.125 Hz处达到峰值。

图3 点A（0.5xmax,0.2ymax,0）相应的液相垂向速度随时间的变化和频谱特性Fig.3 Time series of the horizontal liquid velocity and corresponding frequency series of power spectral density function for point A(0.5xmax,0.2ymax,0)

其他工况下气泡羽流的摆动频率也可以采用上面的方法获得，Q0为125，82.5，42.5 mL/s时位置点A（0.5xmax, 0.2ymax, 0）处液相的垂向速度随时间变化的模拟结果和频谱特性分别见如图4所示。Q0为125，82.5，42.5 mL/s时液相垂向速度的振幅模拟值分别在±0.4，±0.3，±0.2 m/s内，随着曝气量的减少，气泡羽流的摆动幅度在减小。

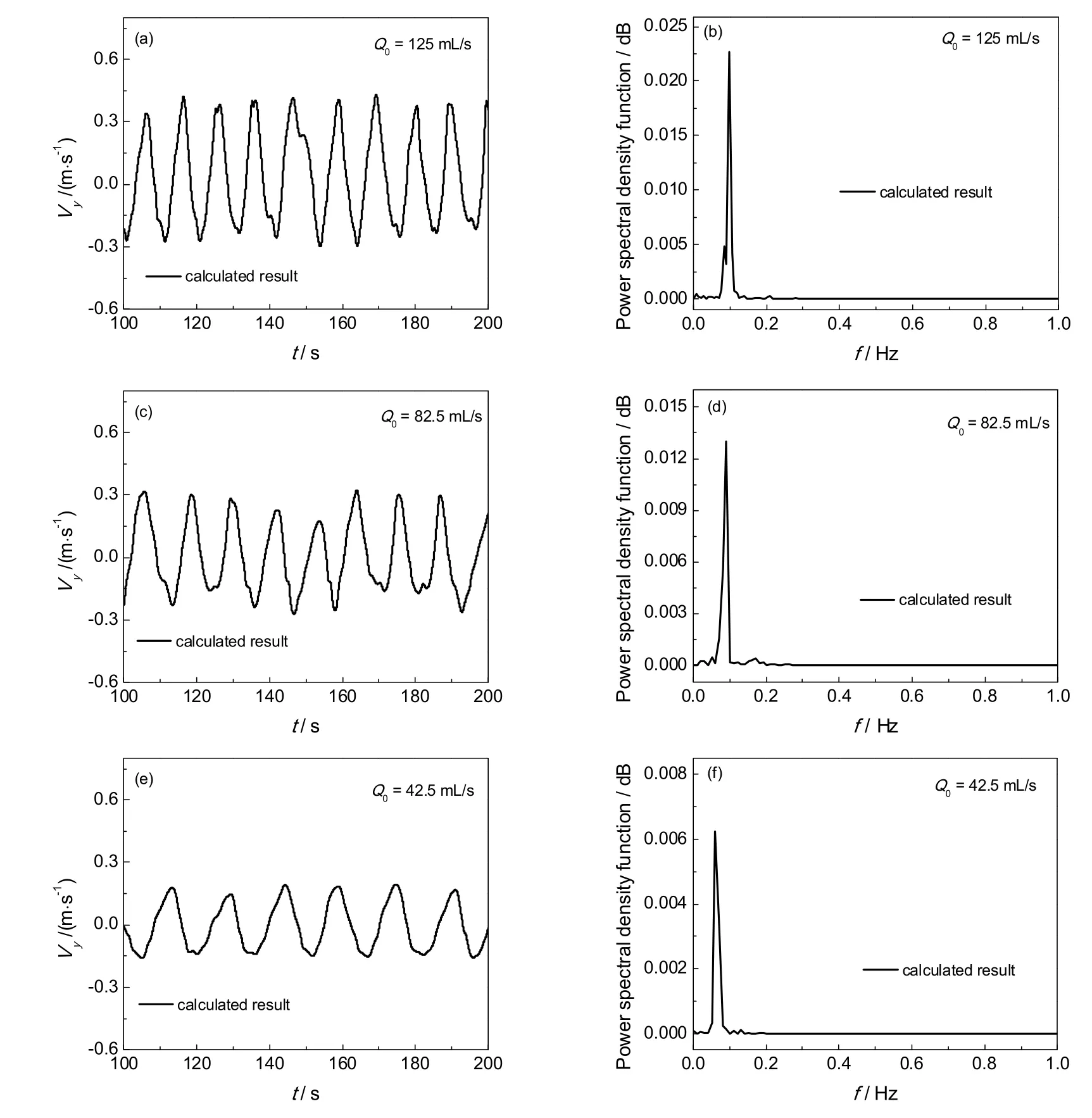
图4 不同Q0下点A相应的液相垂向速度随时间的变化和频谱特性Fig.4 Time series of the horizontal liquid velocity and corresponding frequency series of power spectral density function for point A under different Q0values

Enrique Juliá[18]通过对点A（0.5xmax, 0.2ymax, 0）、B（0.2xmax, 0.2ymax, 0）、C（-0.2xmax, 0.2ymax, 0）、D（-0.5xmax, 0.2ymax, 0）四个位置处的气泡羽流摆动频率进行平均化处理，给出了平均的摆动频率数据。为了和实验数据更好的对比，四种工况下摆动频率模拟数据也采用对点A（0.5xmax, 0.2ymax, 0）、B（0.2xmax, 0.2ymax, 0）、C（-0.2xmax, 0.2ymax, 0）、D（-0.5xmax, 0.2ymax, 0）四个位置处的摆动频率值进行平均化处理获得，对比结果见表4，表中结果显示：对于同一工况，四个位置处气泡羽流的摆动频率基本是一样的，气泡羽流摆动频率的计算值与实验值相对误差为7.2%～12.9%。

表4 气泡羽流的摆动频率与实验数据的比较Table 4 Comparison of experimental and calculated plume oscillating frequency

不同表观气速Ug（Ug为0.52～2.90 cm/s，对应的气流量为42.5～237 mL/s）下气泡羽流的摆动频率见图5，随着气速增加，气泡羽流的摆动频率增加。对不同表观气速（0.52～2.90 cm/s）下总气含率在100～200 s内进行时均处理，可得到时均总气含率变化规律，见图6，随着气速增加，液体的气含率在增加。

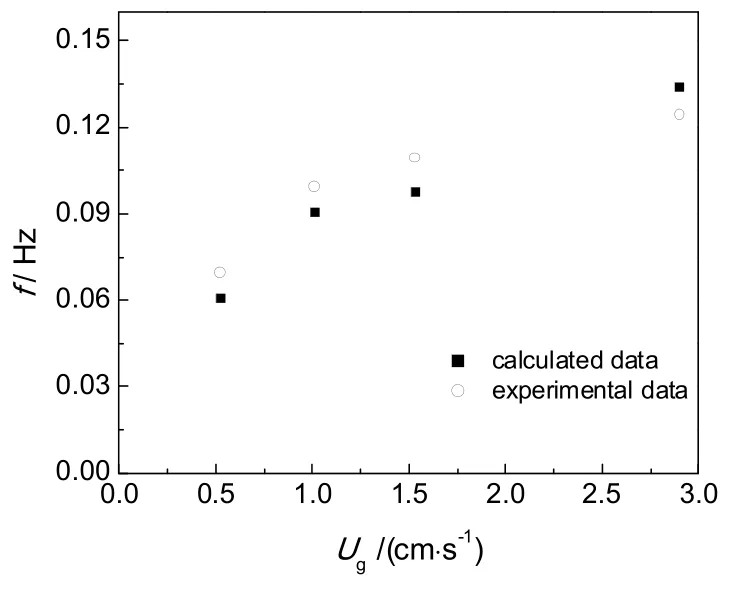
图5 不同表观气速时的摆动频率Fig.5 Oscillating frequency under different superficial gas velocities

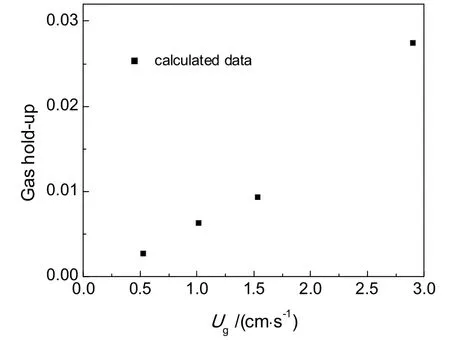
图6 不同表观气速时的总气含率Fig.6 Global gas hold-up under different superficial gas velocities

随着气流速度的增加（曝气量的增大），流场中心区域的速度变大，流场的紊动由中心区域为主扩散到了中心区域和气泡柱的两侧区域，紊动强度增大，同时气泡尺寸总体增加，也加剧了流场的紊动，由此导致了气泡羽流的摆动幅度加大，摆动频率加快；同时，环流涡旋结构的发展更充分，涡两侧的气相速度变大，更多的气泡被带入循环中，液体的气含率增加。

4 结 论

a）本研究采用双欧拉法结合标准的κ-ε方程模型，对鼓泡塔内气液两相流动的动态行为进行了三维数值模拟，能预测气液两相流的摆动特性，获得了气/液相速度、气含率、摆动频率等数据，模拟结果与实验结果基本一致。

b）相间作用力模型影响气泡流摆动频率的计算结果表明：仅考虑阻力的影响，模拟的气泡羽流摆动频率与实验结果吻合较好，两者的相对误差为7.2%～12.9%；虚拟质量力的影响相对较小，可忽略；升力系数为0.5时，与实验值相比，气泡羽流摆动频率的模拟值偏大，升力系数如何合理取值有待进一步研究。

c）相间作用力仅考虑阻力的影响下模拟结果表明：随着曝气量的增加（42.5～237 mL/s），气泡羽流的摆动频率加快，由0.061 Hz增至0.134 Hz，摆动幅度加大，由0.2 m/s增至0.6m/s；同时液体的气含率也相应地增加了。

[1] Becker S, Sokolichin A, Eigenberger G. Gas-liquid flow in bubble columns and loop reactors. Part II. Comparison of detailed experiments and flow simulations [J]. Chem Eng Sci, 1994, 49(24):5747-5762.

[2] Buwa V V, Ranade V V. Characterization of dynamics of gas-liquid flows in rectangular bubble columns [J]. AIChE Journal, 2004, 50(10): 2394-2407

[3] Cheng W, Yuichi M, Fujio Y. Estimation of the liquid velocity field in two-phase flows using inverse analysis and particle tracking velocimetry [J]. Flow Measurement and Instrumentation, 2005, 16(5):303-308.

[4] 宋 策, 程 文, 胡保卫, 等. 气泡羽流空隙率的计算及其不稳定规律的研究 [J]. 水利学报, 2011, 42(4):419-424. Song Ce, Cheng Wen, Hu Baowei, et al. Research on the calculation of void fraction of bubble plume and its instability pattern [J]. Journal of Hydraulic Engineering, 2011, 42(4):419-424.

[5] 肖柏青, 张法星, 刘春艳, 等. 曝气池内气泡羽流附壁效应的试验研究 [J]. 水力发电学报, 2012, 31(4):104-107,112. Xiao Boqing, Zhang Faxing, Liu Chunyan, et al. Canada effect of bubble plume in aeration tanks [J]. Journal of Hydroelectric Engineering, 2012, 31(4):104-107,112.

[6] Delnoij E, Lammers F A, Kuipers J A M, et al. Dynamic simulation of dispersed gas-liquid two-phase flow using a discrete bubble model [J]. Chem Eng Sci, 1997, 52(9):1429-1458.

[7] Darmana D, Deen N G, Kuipers J A M. Detailed modeling of hydrodynamics, mass transfer and chemical reactions in a bubble column using a discrete bubble model [J]. Chem Eng Sci, 2005, 60(12):3383-3404.

[8] Buwa V V, Deo D S, Ranade V V, et al. Eulerian-Lagrangian simulations of unsteady gas-liquid flows in bubble columns [J]. Int J Multiphase Flow, 2006, 32(7):864-885.

[9] Borchers O, Busch C, Sokolichin A, et al. Applicability of the standard k-epsilon turbulence model to the dynamic simulation of bubble columns. Part II. Comparison of detailed experiments and flow simulations [J]. Chem Eng Sci, 1999, 54(24):5927-5935.

[10] Bech K. Dynamic simulation of a 2D bubble column [J]. Chem Eng Sci, 2005, 60(19):5294-5304.

[11] Sokolichin A, Eigenberger G. Applicability of the standard κ-ε turbulence model to the dynamic simulation of bubble columns. Part I. detailed numerical simulations [J]. Chem Eng Sci, 1999, 54(13-14):2273-2284

[12] Pfleger D, Gomes S, Gilbert N, et al. Hydrodynamic simulations of laboratory scale bubble columns fundamental studies of the Eulerian-Eulerian modeling approach [J]. Chem Eng Sci, 1999, 54(21):5091-5099.

[13] Krishna R, Van Baten J M, Urseanu M I. Three-phase Eulerian simulations of bubble column reactors operating in the churn-turbulent regime: a scale up strategy [J]. Chem Eng Sci, 2000, 55(16):3275-3286.

[14] Mudde R F, Simonin O. Two- and three-dimensional simulations of a bubble plume using a two-fluid model [J]. Chem Eng Sci, 1999, 54(21):5061-5069.

[15] Oey R S, Mudde R F, Van H E A. Sensitivity study on interfacial closure laws in two-fluid bubbly flow simulations [J]. AIChE Journal, 2003, 49(7): 1621-1636.

[16] Buwa V V, Ranade V V. Dynamics of gas-liquid flow in a rectangular bubble column: experiments and single/multi-group CFD simulations [J]. Chem Eng Sci, 2002, 57(s 22-23):4715-4736.

[17] 马 霞, 李国栋, 高 扬, 等. 不同曝气量和纵横比下针孔喷射气泡羽流摆动特性的数值模拟研究 [J]. 水动力学研究与进展, 2016, 31(4):433-440. Ma Xia, Li Guodong, Gao Yang, et al. Numerical simulation of the oscillating characterization of needle sparging bubble plume under different aeration rates and aspect ratios[J]. Chinese Journal of Hydrodynamics, 2016, 31(4):433-440.

[18] Enrique Juliá J, Hemandez L, Chiva S, et al. Hydrodynamic characterization of a needle sparger rectangular bubble column: Homogeneous flow, static bubble plume and oscillating bubble plume [J]. Chem Eng Sci, 2007, 62(22):6361-6377.

[19] David C W. Turbulence Modeling for CFD [M]. DCW Industries, 2006:1-522.

[20] Jakobsen H A, Sannaes B H, Grevskott S, et al. Modeling of vertical bubble-driven flow [J]. Industrakl and Engineering Chemistry Research, 1997, 36(10):4052-4074.

Numerical Simulation of the Oscillating Gas-Liquid Flow Experiment

Ma Xia, Li Guodong, Fan Cuixiang, Gao Yang
Xi’an University of Technology, Xi’an 710048, China

The numerical simulation of computational fluid dynamics (CFD) software was used to simulate the dynamic behavior of gas liquid two-phase flow in the bubble column reactor to provide the basis for the design of bubbling tower. Simulation study by Eulerian-Eulerian approach has been made for the oscillation characteristics of gas-liquid two-phase flow in different aeration units in a rectangular reactor. The influence of grid size, time step and interphase force on the simulation was analyzed using the standard k-ε turbulence model for liquid phase and the dispersed phase zero equation model for gas phase. The gas flow rates ranging from 42.5 to 237 mL /s were used for simulation. The results revealed that the gas-liquid two-phase flow exhibited the periodic oscillation law if resistance was considered as the only interphase force. With the increase of air flow, the amplitude and frequency of the bubble plume increased, and the gas hold up increased. The simulated frequency of gas-liquid two-phase bubble flow oscillation was in good agreement with the experimental results, and the relative error was 7.2%-12.9%.

bubble column; gas-liquid flow; the oscillating characteristic; Eulerian-Eulerian κ-ε model

O359

A

1001—7631 ( 2017 ) 01—0073—09

10.11730/j.issn.1001-7631.2017.01.0073.09

2016-12-14;

2017-01-28。

马 霞（1976—），女，高级工程师。E-mail:maxia@xaut.edu.cn。

国家自然科学基金项目（31500340）；环境工程国家重点学科培育学科项目（106-5X1204）。